不同类型短路故障下双馈风机短路电流分析

马 越，陈星莺，余 昆，蒋 宇

（1.河海大学能源与电气学院，南京211100；2.江苏省电力公司，南京210024）

双馈型风机应具备一定的低电压穿越LVRT（low voltage ride-through）能力，即在一定程度的电网电压跌落下，风机需要保持并网运行一段时间[1]。然而DFIG 定子侧直接与电网相连的结构使其对电网扰动尤其是电压跌落故障异常敏感。当电网发生故障时，由于DFIG 定子磁链不能突变，将出现直流分量，进而在转子侧感生出较大的电势，引起转子绕组过电流[2]。如不采取保护措施，容易损坏转子侧变流器并危及风机的安全运行。转子侧撬棒（Crowbar）保护是目前采用较多的保护方法，短路发生后撬棒保护立即将转子绕组短接，起到限制转子电流，保护转子侧变流器的作用。

目前对DFIG 短路电流的研究大多集中在机端三相短路，由于DFIG 定子和转子的电磁耦合，撬棒保护对DFIG 短路电流也有显著影响。文献[3，4]给出在故障下“转子侧电压保持不变”时计算DFIG 短路电流的解析模型，然而机端电压严重跌落下DFIG 配备的撬棒保护能在3 ms 内触发并短接转子，转子侧电压实际上立即下降为零。文献[5]在推导转子侧逆变器退出运行情况下的DFIG 短路电流时，忽略了转子感应电流的影响，对于分析短路电流的暂态分量会造成误差。文献[6]基于DFIG 的Park 模型推导了机端电压跌落转子绕组开路情况下的短路电流表达式。文献[7]在求解电网对称短路下的短路电流时，重点分析了转子保护未动作时的短路电流。文献[8]通过稳态时定子输出的有功和无功功率求得了短路时的转子磁链初值，进而推导了短路电流。由于不对称短路下DFIG 电磁暂态过程比较复杂，对不对称短路下DFIG 短路电流特性的研究还比较少[9～11]。

本文首先基于DFIG 的Park 模型推导了三相短路下计及撬棒保护的DFIG 短路电流解析表达式，并根据该表达式从定子和转子衰减常数的角度分析了DFIG 短路电流特性以及可能影响短路电流的因素，并对理论分析进行了仿真验证。此外还对不对称短路下DFIG 短路电流进行了仿真、分析，为进一步研究不对称短路下的DFIG 短路电流特性提供参考。

1 DFIG 的数学模型及暂态过程分析

由于电网故障期间DFIG 的网侧变流器保持和电网的连接，由DFIG 的结构可知双馈风电机组在短路下输出的短路电流应为

式中：iSDFIG 为定子端输出的短路电流；iGSC为网侧变流器输出的短路电流。文献[2]通过仿真发现，iGSC对DFIG 总短路电流的影响很小，无论是否出现钳位效应都可以用DFIG 定子端输出短路电流来替代双馈风电机组输出的短路电流。

1.1 DFIG 的数学模型

假设DFIG 定、转子三相对称，忽略磁饱和现象，定、转子采用电动机惯例，则在静止坐标系下DFIG 的Park 模型用矢量表示如下[3～8]

电压方程为

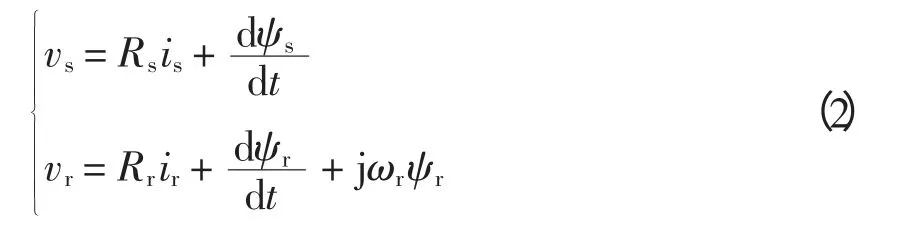
磁链方程为

式中：vs、vr、is、ir、ψs、ψr分别为定、转子电压、电流和磁链；Rs、Rr、Ls、Lr分别为定、转子电阻和电感，且Ls=Ls1+Lm，Lr=Lr1+Lm；Ls1和Lr1分别为定转子漏电感；Lm为励磁电感。

在稳定运行状态下，定子磁链以转速ωn旋转，转子转速为ωr，且

式中，s 为转差率，则由式（3）可得

1.2 电压跌落后DFIG 的暂态过程分析

并网运行状态下DFIG 的定子电压完全由电网电压决定，假设t0时发生三相短路，忽略电网频率波动，则电压跌落前后定子电压可表示[7]为

若忽略定子电阻，由式（2）可得定子磁链为

式中，Vs为定子电压幅值，根据磁链守恒定律，电压跌落后定子磁链将产生暂态直流分量，该分量与机端电压跌落程度以及短路时刻有关。所以故障过程中定子磁链为

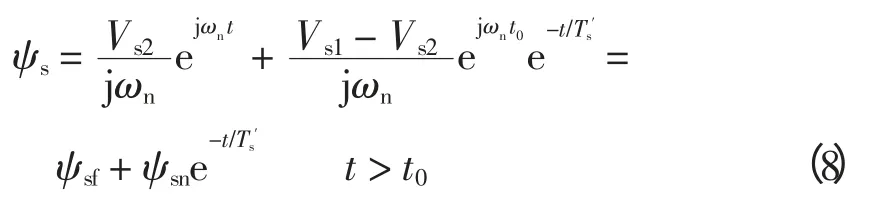
定子磁链和机端电压的关系如图1 所示，外部圆形实线为电压跌落前定子磁链的运动轨迹，内部虚线为电压跌落后定子磁链的运动轨迹。

图1 机端电压与定子磁链关系Fig.1 Relationship between terminal voltage and stator flux

由式（2）和式（3）可得到用定子磁链表示转子电压方程为

把式（7）带入式（10）可得

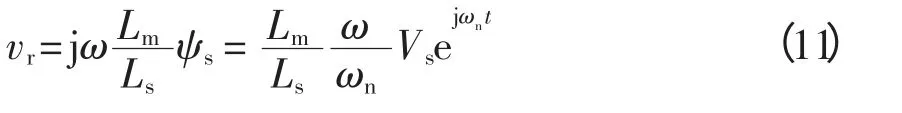
将式（11）变换到转子坐标系下可得

对于三相短路，DFIG 机端电压将严重跌落，转子绕组将感应出暂态电流，这时为了保护转子侧变频器，撬棒保护启动将转子绕组短接，转子电压下降为零。由于转子侧变频器退出运行，风机处于不可控状态[13]。则故障前后转子电压可表示为

在转子参考系下，转子电压方程可写为

若忽略转子电阻，可得到故障前转子磁链为

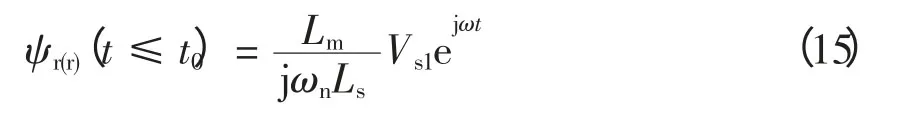
根据磁链守恒定律，故障后转子磁链为

式中，Tr′为转子暂态时间常数，将式（16）转换回静止坐标系为

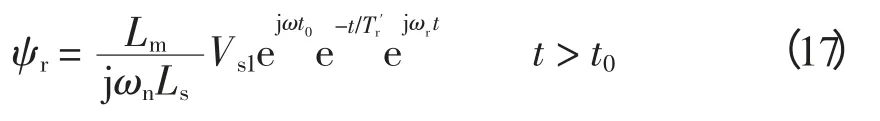
将式（8）和式（17）带入式（5），则可得Crowbar保护动作后退出动作之前，风机未被切除情况下风机短路电流可表示为

由式（18）可以看出短路电流由3 部分组成：第1 部分是以定子衰减常数衰减的暂态直流分量，第2 部分是以转子衰减常数衰减的暂态交流分量，第3 部分是稳态交流分量。

由式（18）还可以看出：暂态直流分量的初值和短路时刻以及机端电压跌落程度有关，电压跌落程度越大，暂态直流分量的初值也越大；暂态交流分量的初值和短路时刻以及短路前定子电压的幅值相关。对于稳态交流分量，由于撬棒保护投入运行后，DFIG 失去了转子励磁，DFIG 的稳态短路电流仅与故障后的机端电压相关，故障越严重，电压下降越多，稳态短路电流幅值越小。

由式（5）可知，当定转子磁链方向相反时，定子短路电流会达到最大，因此出现最大电流的时间与发电机转速有关。当转子转速近似为同步转速时，短路电流峰值一般出现在短路发生后半同步周期点前后。因此最大短路电流估算式为

2 撬棒保护整定值及外电路阻抗对短路电流的影响

2.1 理论分析

以上分析了三相短路下计及撬棒保护的DFIG短路电流，如果短路发生在机端出线端外或者存在故障阻抗，还应该考虑外电路阻抗对短路电流的影响。可以把外电路的阻抗合并至定子绕组的电阻和漏抗上，只要定子总回路的电阻较电抗仍小得多，则故障后的暂态过程和机端短路是一样的[14]。撬棒保护启动将转子绕组短接，故障后的等值电路如图2 所示[15]。

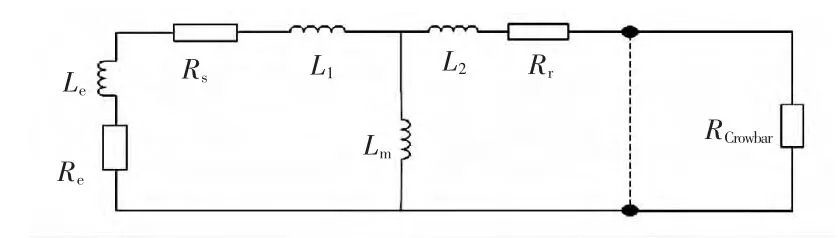
图2 故障后等值电路Fig.2 Equivalent circuit after fault

Re和Le为外电路等值后的等值电阻与电抗，RCrowbar为撬棒保护电阻，RCrowbar与Ze均为折算至DFIG 基准值下的标幺值。

则定转子衰减时间常数[15]为

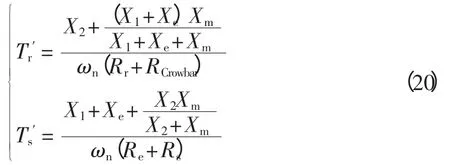
DFIG 参数为：X1= 0.1p.u.，X2= 0.1p.u.，Xm=3.5p.u.，Rs=0.01p.u.，Rr=0.01p.u.。DFIG 的定转子衰减常数e-t/Tr′、e-t/Ts′与RCrowbar及外电路等值阻抗Ze的关系如图3 所示。

图3 定、转子衰减常数Fig.3 Curve of attenuation constant of stator and rotor

由图3（a）可以看出撬棒保护整定值越大，e-t/Tr′衰减越快，也就是说撬棒保护整定值主要影响暂态交流分量的衰减速度。由3（b）看出外电路等值阻抗越大，e-t/Tr′衰减越慢，因此暂态交流分量衰减越慢；由图3（c）看出外电路等值阻抗越大，e-t/Ts′衰减越快，因此暂态直流分量衰减越快。

2.2 仿真验证

在DIgSILENT/PowerFactory 中建立并网运行的DFIG 单机模型，并将其通过变压器和线路1 与外电网相连，系统仿真拓扑结构如图4 所示。

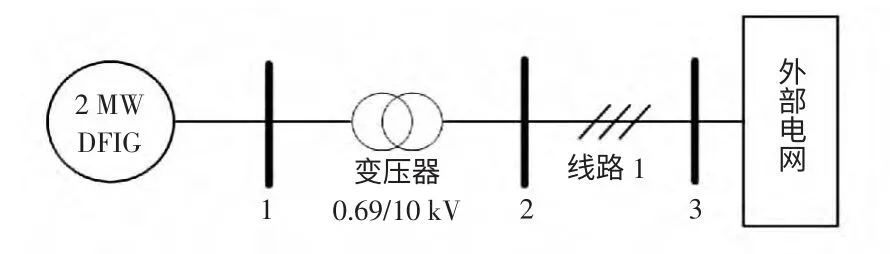
图4 仿真拓扑结构Fig.4 Topology of simulation

（1）母线1 在0 s 时发生三相短路，故障阻抗为0 p.u.，撬棒保护立即启动，0.3 s 时清除故障，随后撬棒保护退出，取不同撬棒保护整定值下的a 相短路电流曲线观察，电流曲线如图5 所示。

由图5 可以看出，在故障阻抗为0 p.u.，机端电压跌落为0 p.u.的情况下，短路电流不存在稳态交流分量，且撬棒保护整定值主要影响DFIG 短路电流的暂态交流分量，撬棒保护电路整定值越大，暂态交流分量衰减越快。

（2）母线1 在0 s 时发生三相短路，撬棒保护立即启动，撬棒保护整定值取0.1 p.u.，0.3 s 时清除故障，随后撬棒保护退出，取不同故障阻抗值下的a 相短路电流曲线观察，电流曲线如图6 所示。

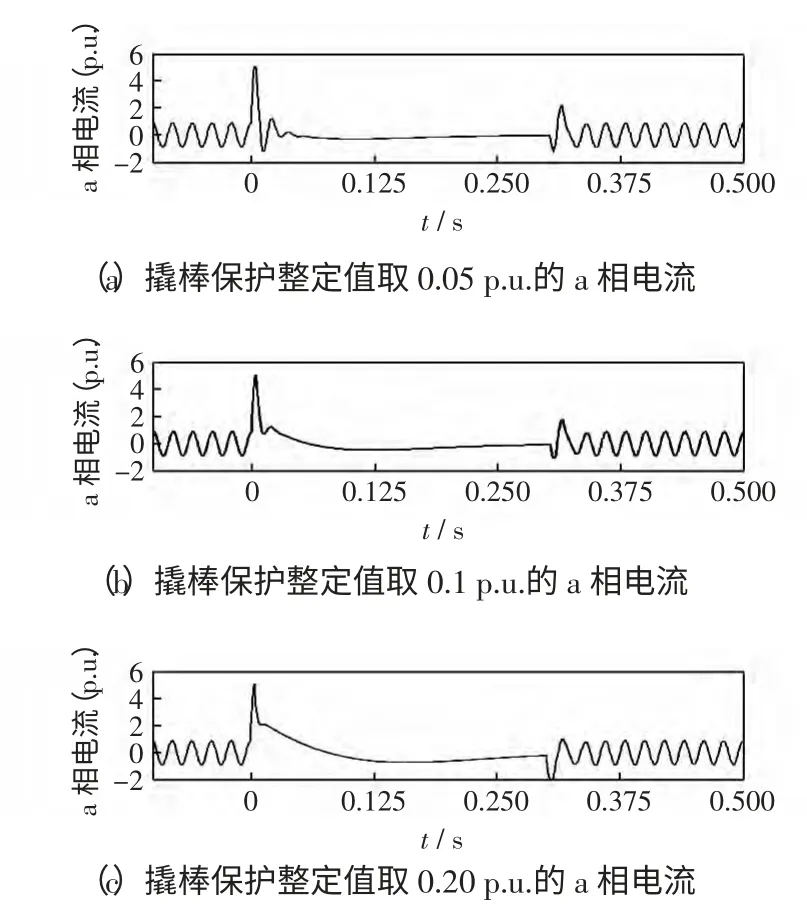
图5 不同撬棒整定值的a 相电流仿真曲线Fig.5 Simulation curve of a-phase current for different crowbar resistances

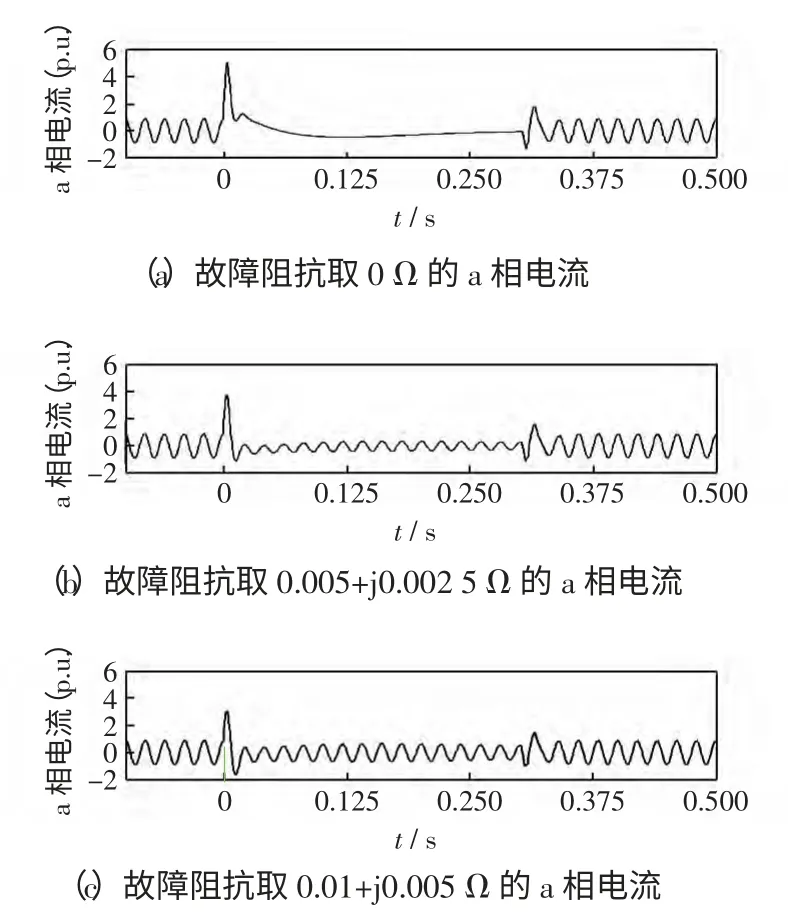
图6 不同故障阻抗的a 相电流仿真曲线Fig.6 Simulation curve of a-phase current for different fault impedance

由图6 可以看出，当短路点的故障阻抗不为零时，由于外部电网对机端电压的支撑作用，DFIG机端电压没有跌落为零，因此DFIG 短路电流存在稳态交流分量。该交流分量的幅值取决于机端电压跌落程度，故障阻抗越大，电压跌落越少，稳态交流分量的幅值越大。

（3）不同位置0 s 时发生三相短路，故障阻抗为0 p.u.，撬棒保护立即启动，整定值取0.1 p.u.，0.3 s 时清除故障，随后撬棒保护退出，取不同短路位置下的a 相短路电流曲线观察，如图7 所示。

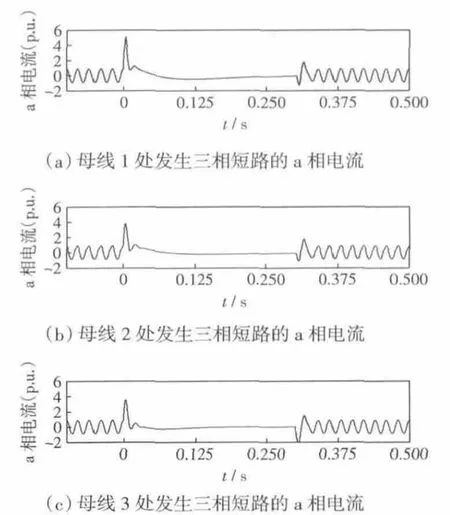
图7 不同短路位置的a 相电流仿真曲线Fig.7 Simulation curve of a-phase current for different fault location

由图7 可看出当短路发生在机端母线1 时短路电流峰值约为5.07 p.u.，当发生在母线2 时短路电流峰值约为3.81 p.u.，当发生在母线3 时短路电流峰值约为3.58 p.u.。说明短路位置和DFIG 的电气距离越近，DFIG 短路电流的暂态峰值越大。

3 不对称短路下DFIG 短路电流分析

电力系统中除了对称故障外，还存在着许多类型的不对称故障，且不对称故障发生比例更高，仅单相接地短路就占约70%[16]。因此研究不对称短路下的DFIG 短路电流特性对全面掌握DFIG 在不同类型电网故障下的LVRT 过程具有重要意义。但由于不对称短路下DFIG 电磁暂态过程的复杂性，本文不推导具体的不对称短路电流表达式，而是利用仿真得到的短路电流曲线，分析不对称短路下DFIG 短路电流的一些基本性质。

（1）仿真算例依然采用本文第2 节图4 所示的单机通过升压变压器接入外部电网的系统。母线1在0 s 时发生a 相单相接地短路，0.3 s 时清除故障，机端电压和DFIG 短路电流如图8 所示。

由图8 可看出母线1 单相接地短路下，由于DFIG 机端电压并不完全跌落到零且各相电压不同，因此故障过程DFIG 短路电流存在较大的稳态交流分量，且a、b、c 三相稳态短路电流幅值不同。

（2）母线1 在0 s 时发生a-b 两相相间短路，0.3 s时清除故障，机端电压和DFIG 短路电流如图9 所示。

8 母线2 单相接地短路的机端电压以及DFIG 短路电流Fig.8 Terminal voltages of generator and short circuit currents of DFIG for single phase to ground located at Bus 2

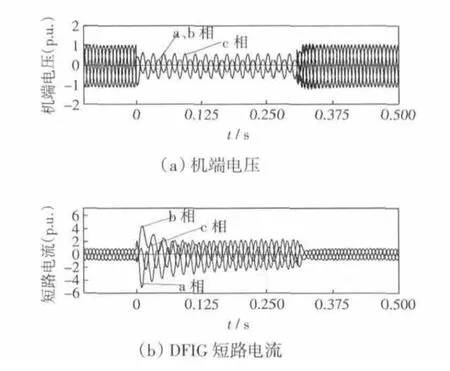
图9 母线2 两相相间短路机端电压以及DFIG 短路电流Fig.9 Terminal voltages of generator and short circuit currents of DFIG for 2-phase short-circuit located at Bus2

由图9 可以看出由于两相相间短路时机端电压也没有完全下降为0，所以短路电流也存在稳态交流分量。但是由于两相相间短路造成的机端电压跌落更严重，因此DFIG 短路电流的暂态峰值比单相接地短路时大。

综上，不对称短路下DFIG 短路电流和短路类型有关，只要机端电压不完全跌落到零，短路电流中将存在较大的稳态交流分量。且越是严重的短路类型，机端电压跌落就越严重，DFIG 短路电流的暂态峰值也越大。

4 结语

采用撬棒保护的双馈风力发电机组在三相短路下的短路电流主要由3 部分组成：以定子衰减常数衰减的暂态直流分量、以转子衰减常数衰减的暂态交流分量以及稳态交流分量。其中：暂态直流分量的初值和短路时刻以及机端电压跌落程度相关，暂态交流分量的初值和短路时刻以及短路前定子电压的幅值相关，稳态交流分量与故障后的机端电压相关，电压跌落越严重，稳态短路电流幅值越小。若机端电压跌落到零，短路电流也将很快衰减为0。此外，撬棒保护整定值、故障阻抗以及短路位置都会对DFIG 短路电流造成影响。

不对称短路下的DFIG 短路电流更加复杂多变，主要和故障类型相关。只要故障下机端电压不完全跌落到零，短路电流中将存在较大的稳态交流分量。且越是严重的短路类型，机端电压跌落就越严重，短路电流的暂态峰值也越大。

[1]朱颖，李建林，赵斌（Zhu Ying，Li Jianlin，Zhao Bin）.双馈型风力发电系统低电压穿越策略仿真（Simulation of LVRT strategy for DFIG wind power system）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（6）：20-24.

[2]邹文仲，袁越，季泽宇，等（Zou Wenzhong，Yuan Yue，Ji Zeyu，et al）.变结构双馈风机的低电压穿越能力（Ability of low voltage ride through capability of DFIG with variable configuration）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（4）：1-6，12.

[3]Morren J，de Haan S W H. Short circuit current of wind turbines with doubly fed induction generator [J]. IEEE Trans on Energy Conversion，2007，22（1）：174-180.

[4]翟家俊，张步涵，谢光龙，等（Zhai Jiajun，Zhang Buhan，Xie Guanglong，et al）.基于撬棒保护的双馈风电机组三相对称短路电流特性（Practical calculation model of three-phase short-circuit current for doubly-fed induction generator）[J]. 电力系统自动化（Automation of Electric Power Systems），2013，37（3）：18-23.

[5]欧阳金鑫，熊小伏（Ouyang Jinxin，Xiong Xiaofu）. 接入配电网的双馈风力发电机短路电流特性及影响（Characteristics of short-circuit current of wind turbine driven DFIG and its impacts on grid-connected distribution network）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（23）：106-110，123.

[6]Lopez J，Sanchis P，Roboam X，et al. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips [J]. IEEE Trans on Energy Conversion，2007，22（3）：709-717.

[7]欧阳金鑫，熊小伏，张涵轶（Ouyang Jinxin，Xiong Xiaofu，Zhang Hanyi）.电网短路时并网双馈风电机组的特性研究（Characteristics of DFIG-based wind generation under grid short circuit）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（22）：17-25.

[8]李辉，赵猛，叶仁杰（Li Hui，Zhao Meng，Ye Renjie）. 电网故障下双馈风电机组暂态电流评估及分析（Evaluation and analysis of transient current of a DFIG wind generation system under grid fault）[J]. 电 机 与 控 制 学 报（Electric Machines and Control），2010，14（8）：45-51.

[9]苏平，付纪华，赵新志，等（Su Ping，Fu Jihua，Zhao Xinzhi，et al）.电网不对称故障下双馈风力发电机组穿越控制的研究（Research on asymmetrical faults ridethrough control of doubly fed induction generator）[J].电力系统保护与控制（Power System Protection and Control），2011，39（16）：101-106.

[10]Lie Xu. Coordinated control of DFIG's rotor and grid side converters during network unbalance [J]. IEEE Trans on Power Electronics，2008，23（3）：1041-1049.

[11]Johan M，de Haan S W H. Ride through of wind turbines with doubly-fed induction generation system [J]. IEEE Trans on Power Electronics，1995，10（4）：435-441.

[12]Akhmatoy V.Induction Generators for Wind Generators for Wind Power [M]. Brentwood Essex：Multi-Science Publishing Company，2005.

[13]Pannell G，Atkinson D J，Zahawi B. Minimum threshold crowbar for a fault ride through grid code compliant DFIG wind turbine [J]. IEEE Trans on Energy Conversion，2010，25（3）：750-759.

[14]何仰赞，温增银.电力系统分析[M].武汉：华中科技大学出版社，2010.

[15]杨国生，李欣，周泽昕（Yang Guosheng，Li Xin，Zhou Zexin）.风电场接入对配电网继电保护的影响与对策（Impacts of wind farm on relay protection for distribution network and its countermeasures）[J].电网技术（Power System Technology），2009，33（11）：87-103.

[16]张磊（Zhang Lei）.基于UPFC 的非对称短路故障电流限制研究（Research on Limiting of Asymmetric Short-Circuit Fault Current Based on UPFC）[D].昆明：昆明理工大学电力工程学院（Kunming：School of Electric Power Engineering，Kunming University of Science and Technology），2009.