天气和气候预报：面临一个新拐点？——《哲学学报A》关于天气和气候预报的随机模拟专辑带来的启示

贾朋群 赵大军

天气和气候预报：面临一个新拐点？
——《哲学学报A》关于天气和气候预报的随机模拟专辑带来的启示

贾朋群 赵大军

目前的天气和气候模式显示了很多令人吃惊的预报技巧，例如，从提前数天的台风路径预报到提前几个月预报厄尔尼诺现象的出现等。但是，模式模拟和预报的误差随着预报时效而增加，并非源自我们对天气和气候演变所遵循规律认知程度的下降。对大气运动规律的认知，早在100多年前就由一组偏微分方程几近完美地进行了描述。模式误差的增加实际上更多地和模式用数值方法求解上述方程组时，由于大气非线性和多尺度的本质，近似解的偏差随着数值积分的进行而不断增加联系在一起。其中，采用参数化处理次网格过程或方程组中无法解析的项，以及后者与模式可解析的动力框架部分之间的相互联系和作用的计算实现的不足，无疑是误差最重要的来源。

一些学者从大气运动的随机性出发，试图在理论上获得突破，即明确随机过程在多大程度上充满和规范着大气运动，同时要在模式的每一步积分运算中将这样的随机内容体现出来。2013年这些学者在牛津大学召开的“天气和气候预报的随机模拟和计算研讨会”上进行了对话和头脑风暴，会议上诞生和逐步清晰化的一些新理念和新思想，蕴含在2014年6月出版的皇家学会《哲学学报A》“天气和气候预报的随机模拟和节能计算”专辑（图1），可能会引发天气气候模拟界进一步的思考。

本文依据研讨会相关内容（研讨会网页，https://www.maths.ox.ac.uk/）及专辑导语和主要文章，试图解读未来模式发展中的“随机”要素。

“一些学者从大气运动的随机性出发，试图在理论上获得突破，即明确随机过程在多大程度上充满和规范着大气运动，同时要在模式的每一步积分运算中将这样的随机内容体现出来。”

一、“随机”模拟或让动力气象回归简单

动力气象学，虽然其诞生要追溯到20世纪初皮耶克尼斯提出“天气预报问题是一组物理方程的初值问题”的构想，同时给出了基于经典物理学的大气运动方程组。然而，早期气象学家苦于这个包含了至少7个变量的方程组太复杂，以及气象数据的匮乏和缺少有效计算方法，在随后的近20年时间里，方程组被束之高阁。尽管如此，皮耶克尼斯创造性地给出的这组控制大气运动的偏微分方程，仍然意义重大。

真正尝试运用皮氏方程组进行大气运动规律分析，或者简言之进行天气预报的，是20世纪20年代的理查孙。正是理查孙，在人类计算还停留在手工和借助计算尺等简单工具时代，将皮氏偏微分方程组离散化到可计算的网格上。在这一过程中，存在一些用公式表达的，却无法用格点解析出来的量，皮氏模仿分子粘性和扩散，借助提出的“涡旋粘度”和“涡旋扩散”等概念进行了参数化。而分子粘性和扩散的理念，与当时业已成熟的流体动力学理论，例如，布西内斯克假定和普朗特的混合长理论等半经验理论一脉相承。

理查孙试图手工计算求解偏微分方程组并做出天气预报失败后又过了20多年，在20世纪40年代电子计算机出现曙光之时，查尼等人成功地让方程组促成了数值天气预报的真正诞生，不同特色的天气和气候模式也随后不断出现。尽管目前的各类模式，要比前辈们当初的计算复杂得多，但是，理查孙最早提出的两个理念依然是基础：一是所谓“经典数值假定（canonical numerical ansatz）”，即动力核心；二是基于动力核心截断尺度变量和一些自由参数构成的参数化公式。

图1 《皇家学会哲学学报A》专辑

上述普适的公式和概念，虽然从数值预报操作层面上历经从准地转到非静力等各种近似，使得方程组从简单到复杂递进，这样的递进却始终没有离开前述基础理念，或者说仍然建立在这样理念基础之上。如果说改变，那就是随着模式性能的大幅度提高，其复杂性和时

空分辨率等的提高，让模式运转的计算成本一路飙升（图2）。一方面，因为一些中尺度过程能够被模式捕捉到，从而进入动力核心的内容在逐步增加；另一方面，动力核心无法解析的、在模式中用参数化方式表示其总体效果的过程，也因为理论进展、观测试验补充的数据和经验等，其误差在逐步减少。

实施天气和气候数值预报模式运行的硬件平台，随着计算机技术诞生以来的3次飞跃，从矢量计算到大规模平行计算，再到多核心计算时代，在计算能力获得跳跃的同时，其能耗也在迅速增加（图3）。这一方面使得继续通过减少网格间距换取参数化不准确性下降的代价更加昂贵——例如目前气象界议论的即将诞生的百亿亿次计算能力（exascale computational capability），其能源消耗也将达到100兆瓦，大约是一个10万人的城镇的用电量；另一方面，即使在2020年前后我们能够运行百亿亿次计算机，模式对模拟云变化这类小尺度过程也无能为力。

面对预报急迫的需求和仅依靠计算平台升级可能面临难以承担的能源成本的格局，新的改进预报思路和创新性的计算范式开始浮现。这样的计算范式的基础，是基于观测到的很多气候变量具有的幂律结构（power-law structure），该结构表明并不存在自然的途径描述某个变量是“大”还是“小”，也就是说，在数值模式中将可解析和不可解析的变量区分开来并不存在一个绝对的基础。基于这样的考量，在对一个无法解析过程的参数化计算中，加入本质上是随机的一个表示，使得这样的划分在数值模式中减少了人为性。以此为出发点，发展随机参数化则又涉及一些更加深入的问题：例如，作为尺度的函数的动力核心中的变量的真实信息内容到底是什么？动力核心在截断尺度附近变量的信息内容不能被任意给出，这是因为这些内容受到无法解析的参数化包的随机性的巨大影响。当尺度较大的时候，随机性的影响将减小，实际信息内容将增加——但是减少的速度又有多快？目前我们知道，在三维浅幂律谱系统中，信息内容随尺度的增加可能是缓慢的。

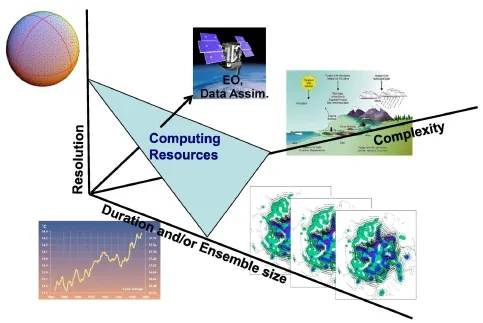
图2 天气气候模式的计算量由预报时效/集合规模、模式复杂性、数据同化过程和分辨率等因素共同决定

图3 高性能计算技术的3次突破（a）和2010年世界500强超级计算机的能耗（b）

原则上，对依赖于尺度的信息内容的认知和下一代天气和气候模式的设计有极为密切的关系。因为目前以及未来可能的超级计算机具有高耗电特点，未来的模式需要尽可能高效。对依赖尺度的信息内容的认知将有利于优化计算的精

度，即在天气和气候模式中，变量表征为尺度的函数。对依赖尺度的信息的认知，还有助于确定是否需要完全由动力核心的数值计算完全决定预报。通过简化传统假定，包括动力核心中所有方程用双字节确定论计算，以及所有变量用双精度浮点实数表示等，一个新的基于变量精度和准确性随尺度变化的概念的计算范式浮出水面。这样的理念如果成功，天气气候模式在更贴近实际的同时，计算方案中一直被复杂化的势头也将做出相反的调整，对随机过程深入的认识和在模式中应用，很可能带领人们在模拟实践中，从复杂回归简单。

二、建立在随机理念上的云解析方案：直指天气气候模拟的瓶颈

毫无疑问，在预报模式借鉴更多随机或概率思想方面，天气模式走得更早，也更远些。其中，集合预报模式在世界上最主要的预报中心成为主流业务预报手段就是明证。但是，集合预报从根本上来说，其随机要素主要体现给出具有误差概率分布的初始场，以及最后基于单模式或多个模式的结果，给出预报的统计规律。然而，集合预报只是较好地解决了误差与预报不确定性之间的联系，而其每一次运算依然是传统数值预报的范式，并非是真正引入大气中固有随机过程及其与其他可解析过程相互作用之路。

帕尔默是对大气可预报性进行过深入研究的气象学者之一，作为2013年牛津大学会议的召集人和《皇家学会哲学学报A》专辑的3位特约编辑之一，他基于对大气运动中随机过程及其与可预报性的认识，从非线性随机过程的角度，提出了一个能够快速实现云解析天气气候模拟的解决方案。

在帕尔默的方案中，受到相对浅的大气几百千米及更小尺度能量幂律谱的启发，通过模糊化动力核心和次网格参数化之间的惯常边界，指出基于随机—动力系统的天气和气候模拟计算方案，要优于确定性模拟计算。此外，由于动力核心中高波谱要素在时间积分中，具有本质上的随机性，因此，如果所有计算不问尺度大小都完全用确定方式进行，并且所有变量都用最大数值精度（即实际运算中用双精度浮点数）表示，将有过度计算的嫌疑。在百亿亿次计算时代即将来临的时候，帕尔默的方案在实际的计算中，最高精度的变量仅限于被解析的动力部分，而随机参数化和引入的随机性等，则用近似计算完成（图4）。这样的处理，既让更多的计算资源着重于核心的动力计算，实现能源和计算均高效，又引入了云解析天气和气候模拟的随机处理理念，在这部分更少占用计算资源的计算中，却使得随机过程在模拟中具有更加重要的意义和作用。

图5更加具体地描述和说明了云解析随机模拟方案，其中不直接利用确定性公式来表征次网格尺度过程，而是利用简化的动力系统来表征，其在总体上与确定性动力系统保持一致，同时又能够提供足够的随机特征。从机器计算的角度来看，利用随机学概念来表征这种不可预报性要容易的多，机器处理随机系统的统计特征要比确定性系统的统计特征要更可信。也许最好的方法是将随机动力学和确定性动力框架结合起来，此时在处理次网格尺度平流时要比总体平均的处理方式要强。这是一种使动力框架和参数化处理之间的界限模糊化的处理方式，更有可能带来让还不够完美的模式模块之间更加和谐和统一的新思路。

在帕尔默的上述方案中，他进一步提出使用定义在恰当尺度格点上（比动力核心的定义格点要小得多）的随机对流单体自动机（cellular automata）来表征模式不可分辨的对流云系统。这种随机对流单体的发展是否可控，其发展的概率由格点尺度变量决定。具体某一个对流单体的生命史随机决定，但是当临近的对流单体是发展的，其自身的生命史相应增长。如此可使有组织的对流系统比分散独立的对流系统有更长的生命史。这些有组织的对流系统可向模式可解析格点传输能量。对于这些对流单体而言，利用墨西哥帽小波变换方法可以通过格点尺度的风将活跃的对流单体从一个网格平流到另一个网格。通过这种方法，次网格尺度的动力特性可以很容易地被编码在方案中，基于这一概念，一个可供业务运行的随机对流方案已经初步形成。

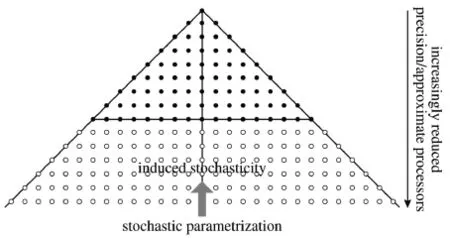
图4 随机参数化方案示意图。在球谐系数的三角形截断中，上面的实心圆点表示计算中用高精度表示的模式的主要尺度变量，下面的圆圈则表示针对次网格尺度以及引入的随机过程，采用低精度计算的部分

另一种基于网格的对流云系统非相互影响的随机方法，是利用泊松概率分布来表示次网格尺度的对流系统，即非相互作用要素间的简单统计关系。也有学者更是通过综

合积云、层云以及深对流云发展了随机多类云网格模式，从而将这种方法推广，各类云之间的转换是通过马尔可夫链过程确定。还有人另辟蹊径，认为次网格过程可以利用具有明确物理意义，但是低计算精度的方程来计算。研究者从电脑游戏动画师使用的技术中得到灵感，利用“适当”的流体方程组来模拟流体流动，即用相对简化的方法来防止能量不守恒，以此确保模拟看起来足够逼真。

专辑中次网格尺度随机动力学模式的另一个范例，是欧洲中期天气预报中心的随机全倾向扰动参数化方案（SPPT）。在SPPT中，确定性的参数化倾向P被（1+e）P所取代，其中e表示球面空间中马尔科夫链过程中的某个物理量场，具有特定的时空自相关系数。这种乘法因子形式的噪声结果与前面提到的粗网格收支研究大体一致。SPPT方案已被证明可以提高中期概率预报和季节概率预报技巧，同时降低天气尺度系统的背景误差。

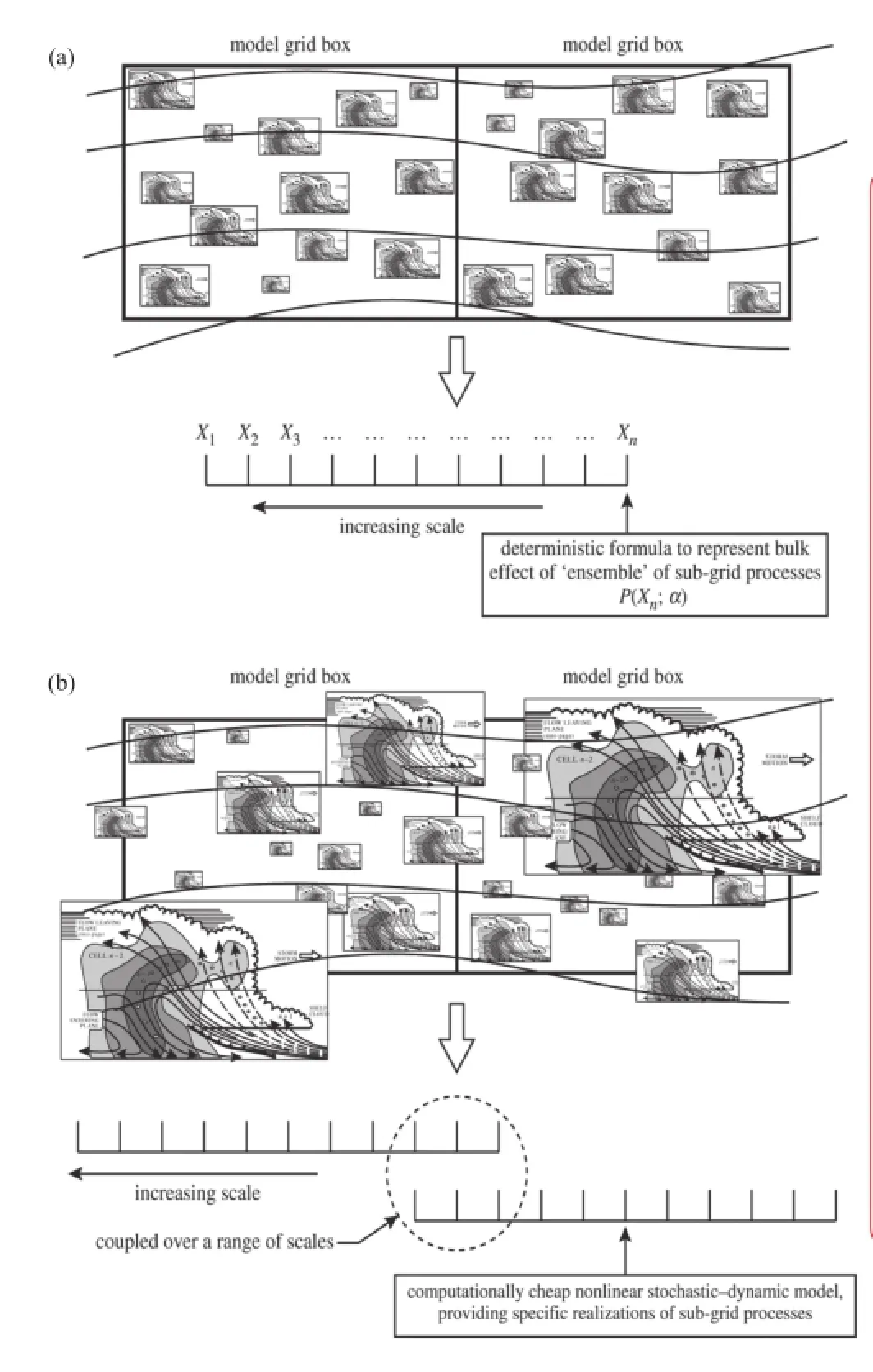
图5 随机模拟方案概念图：(a) 在可解析和无法解析尺度之间存在严格的尺度分离，以示意确定性参数化的概念；(b) 在可解析和无法解析尺度之间没有尺度分离，以示意随机参数化的概念，这更接近实际的情况

从1963年洛伦兹揭示了大气混沌现象开始，到1976年世界上第一个随机气候模式的出现，已经宣告1905年爱因斯坦开创的随机动力学在气象学领域已经有了回声。

三、结果讨论：随机性引领一个新方向

哲学家维特根斯坦曾经讲过：“我的语言的界限意味着我的世界的界限”。梳理气象学家的天气、气候模式中的“语言”，我们可以大致领悟气象科学到目前依然是确定预报主导，对应的是牛顿经典物理学的语言。然而，从1963年洛伦兹揭示了大气混沌现象开始，到1976年世界上第一个随机气候模式的出现，已经宣告1905年爱因斯坦开创的随机动力学在气象学领域已经有了回声。

气象科学发展到现在，很多已知的天气现象，或者是对其探测、或者是对其成因的认识，往往是不充分的或者二者之间并不对称（图6）。面对这样的复杂科学问题，统计的理念和方法帮助气象学者不断获得认识上的改进和实质上的进步。当前，业内人士并不陌生的随机概念，借助相关学科“自组织”系统模型，又有可能被我所用，而且不仅仅是在初始值或结果统计中借用，而是深入到天气气候模式内部，用非高精度的随机计算，描述次网格和本质上是随机的大气及边界层过程，从而与大气中存在的多种随机扰动因子实现某种意义上的协同。这样做的启示是在说明, 大气过程是确定的, 也是随机的，而模拟大气运动的模式，在确定和随机（参数化）之间的界限，在随机理念渗透和模式分辨率提高的双方向的努力下，走向模糊并可以进一步打通（图7）。

无论是2014年的专辑，还是2013年牛津大学的研讨会上，气象模拟学者在讨论预报的科学问题同时，也在讨论计算技术问题。在牛津大学，第一次出现了一边是天气和气候模拟学者，另一边是计算机科学家，坐在一起探讨天气和气候预报中的不精确和随机计算的作用等深刻问题。这样的场景很容易让我们想起20世纪40—50年代，发生在普林斯顿高级研究院数值天气预报伴随世界上第一台电子计算机的研制而获得成功的历史。那时，冯·诺依曼等计算数学家甚至加入了气象队伍，直视气象预报模式的运转。正是那样的跨学科攻关，带来了现代气象科学实质上的进步，气象科学也成为最先利用计算机推动

学科建设，并通过应用于各种模式的开发，提高天气气候预报水平，让社会受益的样板学科。

本文介绍的主要来自欧洲国家的在天气气候模式中，加入更多“随机”要素从而获得更好的预报效果，或者退一步讲，在预报能力持平的情况下大大节省计算资源，从而在相同的计算消耗下获得更好的预报。这样的思想，某种意义上放大了在集合预报中就出现的气象预报中的“统计”思维。气象中的统计或概率思维实际上更接近自然本质，但是在科学层面上也面临很多挑战。2014年7月，美国著名的Science杂志宣布，该杂志所收到的所有统计类论文，在同行评议过程中增加一个额外的统计验证环节①杂志在具体操作时，与美国统计协会共同成立了一个7人专家评审小组，将编辑或审阅人标记为统计类文章，邀请外部统计学者进行附加审核。。世界上其他一些科技期刊，例如Nature在2013年4月，也推出类似的做法，起因就是大多数依据统计和数据分析方法获得的研究发现，因为无法再现，从而有可能掩盖了在数据分析中本质性的错误。由此我们可以想象和质疑，专辑文章预示的更多“随机”要素进入预报模式，其预报的未来天气气候，会不会因为具有太多的“随机”性而让我们无所适从。

实际上，集合预报中的很多做法，已经为我们提供了有益的避免产品层面上过多“随机”因素的思想和做法，而借鉴数据同化中的“窗口”，一些随机过程可能依据的类似“白噪声”的规律也可以提示我们不断改进对随机过程的描述和在模式中实现。此外，随着数值预报历史资料累计得到的“大数据”，能够提供给我们天气气候在一些形势“转化期”中的相似性，也有可能引导我们更加审慎、也更加有把握地面对“××年一遇”的天气气候的预报问题。

图6 不同天气现象的探测认知程度和其在气候模式中形成原因的认知程度，上部的虚线表示认知的“无边界”

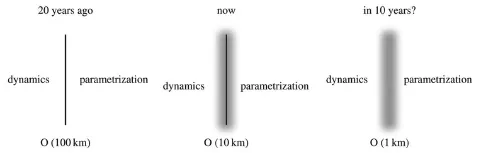
图7 天气气候模式中动力和参数化处理过程之间的界限的模糊

（作者单位：贾朋群，中国气象局气象干部培训学院；赵大军，中国气象局）

深入阅读

André J-C, Aloisio G, Biercamp J, et al. 2014. High-performance computing for climate modeling. Bull Amer Meteor Soc, 95: ES97–ES100.

Palmer T, Düben P, McNamara H. 2014. Stochastic modelling and energyefficient computing for weather and climate prediction. Phil Trans R Soc A, 372: 20140118.

Reeves, Robert W. 2014. Edward Lorenz revisiting the limits of predictability and their implications: an interview from 2007. Bull Amer Meteor Soc, 95: 681–687.

Wuebbles D, Meehl G, Hayhoe K, et al. 2014. CMIP5 climate model analyses: climate extremes in the United States. Bull Amer Meteor Soc, 95: 571–583.

陈超辉, 李祟银, 谭言科, 等. 2013. 随机强迫对集合预报效果的影响研究. 气象学报, 71 (3): 505-516.

宣捷. 2000. 大气扩散的物理模拟. 北京:气象出版社.

周秀骥. 2005. 大气随机动力学与可预报性. 气象学报, 63(5): 806-811.