集合预报方法在暴雨研究和预报中的应用
2014-03-02杜钧李俊
杜钧李俊
(1 美国国家海洋和大气管理局 国家环境预报中心, 美国;2 中国气象局武汉暴雨研究所, 武汉 430074)
集合预报方法在暴雨研究和预报中的应用
杜钧1李俊2
(1 美国国家海洋和大气管理局 国家环境预报中心, 美国;2 中国气象局武汉暴雨研究所, 武汉 430074)
机理了解不够和可预报性问题的忽略是暴雨预报不尽人意的两大原因。主要讨论第二方面,即如何面对和处理可预报性问题,这对如何提高现有数值预报的价值、做好气象服务尤其重要。根据作者多年的研究和实践经验以及直接接触的一些研究和方法,简要地总结了数值集合预报方法在暴雨研究和预报中的应用,具体包括以下四个方面:(1)暴雨集合预报系统的建立:初值和物理扰动、成员数、模式分辨率、资料同化和“虚拟”集合预报;(2)预报方法:集合异常预报法、再预报相似集合法和台风路径聚类法;(3)在预报后处理与订正中的应用:平均、成员排序与最佳成员法、加权平均、概率匹配平均法和集合动力因子法;(4)对暴雨天气系统的机理分析与模式初值的改进:初值扰动差异分析和集合敏感性法、目标观测。希望国内气象业务部门能在日常业务中借鉴以上方法以提高暴雨预报和服务水平,为今后的研究工作提供一个新的起点、方向和方法,这包括指导现有的一些业务集合预报系统今后的进一步完善。
暴雨,集合预报,预报订正,天气诊断,目标观测,资料同化
1 引言
暴雨是中国的主要重大灾害性天气之一,它造成巨大经济损失并威胁人类的生命[1],大量的科研力量也因此集中在同暴雨有关的工作上[2]。譬如,随便翻阅一本中国的气象专业杂志,就可看到有关暴雨的文章;国家专门设立了研究暴雨的专业研究所(即中国气象局武汉暴雨研究所,http://www.whihr.com.cn)。虽然如此,目前的暴雨预报仍然不尽如人意,远远不能满足气象服务的需求[3]。原因可能有两大方面:一是对暴雨产生的机理了解不够,特别是对它在不同情形下的中、小和微尺度的物理过程没有完全了解和掌握[4],因此还不能在数值模式中精确地描述这些过
程,导致模式没有能力预报出所有不同类型的暴雨;二是没有科学地面对和处理其可预报性问题,强降水过程往往是在极其复杂过程下多尺度系统非线性相互作用下的一种综合结果,任一环节如初值(包括大气、下垫面和侧边界)、物理过程和参数化方案以及模式的计算处理上的细小差别都有可能导致预报结果的重大差别[5-6],所以即使一个模式有能力来预报它,其预报的不确定性也很大[7-8]。而预报的不确定性问题又在当前的预报实践中被忽略[9-10],结果使公众和用户得不到关于预报的全面信息(即各种可能性及其可信度)而失去本来可以做出更优决策的机会[11-12]。
本文的讨论主要集中在第二方面,即如何面对和处理其可预报性问题,这一问题对如何提高现有数值预报的价值和做好气象服务尤其重要[11-12]。集合数值预报方法是一种专门用来定量估计预报误差也即预报不确定性的动力学方法[7,13-14],因此,它在暴雨这类预报误差很大的预报制作过程中大有作为。需要强调的是,集合预报的主要目的是针对某一特定的预报系统来实时定量地模拟该系统对任一气象要素随时间、空间以及天气系统而变化的可能预报误差的分布,并不是要做出一个更准确的单一值预报[7-14],第2和第3节讨论有关“预报误差的预报”或称为“可预报性的预报”的内容;虽然如此,集合预报的第二类作用也确实可以改进预报本身的准确性,这主要通过两种途径来实现:一是通过对原始预报的后处理,如集合平均方法[15]来过滤掉可预报性低的预报信息和预估成员相对优劣法[16]来选取最佳成员或进行加权平均等(第4节),二是通过预报不确定性信息的反馈来改进模式初值而间接地提高预报的可预报性,达到提高预报精度的目的,如基于集合预报的目标观测[14,17](第5节)和资料同化[18](第2.3节)。本文简要地总结了集合数值预报方法在暴雨研究和预报中的应用,具体包括四个方面:(1)暴雨集合预报系统的建立:初值和物理扰动、成员数、模式分辨率、资料同化和“虚拟”集合预报;(2)预报方法:集合异常预报法、再预报相似集合法和台风路径聚类法;(3)在预报后处理与订正中的应用:平均、成员排序与最佳成员法、概率匹配平均法和集合动力因子法;(4)对暴雨天气系统的机理分析与模式初值的改进:初值扰动差异分析和集合敏感性法、目标观测。第6节则对上述内容做一总结和讨论。
本文是根据作者多年的研究和实践经验以及直接接触的一些研究和方法的总结,虽然它涉及范围较广,但并不是,也不奢望是对现有文献的全面回顾。通过总结,希望能起到两个作用:(1)气象业务部门能在日常业务中应用众多行之有效的方法来提高暴雨预报和服务水平;(2)为今后的研究工作提供一个新的起点、方向和方法,这包括指导现有的一些业务集合预报系统的进一步完善。
2 暴雨集合预报系统
2.1 初值扰动
早期研究[15,19-20]表明,降水预报对模式的初值很敏感,因此基于初值的集合预报系统在强降水预报上不但能改进单一值的确定预报,也能提供各降水量级较可靠的概率预报。我们的研究[21]进一步表明初值扰动场的空间结构比扰动幅度的大小(当然不能虚假地过大)对集合预报离散度的作用更重要。因为大暴雨经常同对流系统活动有关,为了使初值扰动结构中能反映对流系统,陈静等[22]在应用增长模繁殖法(BGM)[23-24]的扰动产生过程中用两个具有不同对流参数化物理方案的模式预报之差(传统上用两个具有相同物理过程的模式预报之差)来产生初值扰动场,结果表明由此产生的扰动结构能较好地反映对流活动区而进一步改进集合预报对暴雨预报的效果。关于不同空间尺度的初值扰动场对降水集合预报离散度影响的研究表明[25],虽然较大尺度(波长64~90km)的初值扰动场相对较小尺度(波长2~8km)的扰动场而言对集合成员预报的总离散度起主导的作用,但它对小尺度(波长8~32km)预报误差的模拟似乎贡献很小或无能为力;而较小尺度的扰动场却可以模拟出小尺度(波长8~32km)以及中尺度(波长64~512km)的预报误差。这一结果在没有明显天气尺度系统作用下,即弱背景环流形势下的强降水(如对流降水)尤其明显,这时初值扰动中较小尺度的结构比较重要;而在强天气尺度系统控制下的强降水(如锋面降水),较大尺度和较小尺度初值扰动场对模式小尺度预报误差的作用都差不多,这时初值扰动中小尺度的结构就相对不重要。上述结果也许可以部分解释我们在一项研究中所看到的为什么直接用高分辨率的区域模式所生成的初值扰动场其集合预报效果要优于从低分辨率全球集合预报系统降尺度而来的初值扰动[26]。为了综合利用大、小尺度扰动的各自优点,NCEP的短期集合预报系统(SREF)釆用了大、小尺度混合的初值扰动场:即在区域模式生成的较小尺度扰动场(16km)基础上再叠加上由全球集合预报系统生成的较大尺度扰动场(55km),结果表明这样做可以有效地提高集合离散度的增长率和集合预报的效果。为了使初值扰动同侧边界扰动相匹配,奥地利气象局的区域集合预报系统也釆用了这种分別来自全球和区域集
合预报的大、小尺度混合的初值扰动方法,取得较好效果。
研究中发现夏季午后雷阵雨以及近地面气温的预报对模式土壤湿度初值很敏感[27-29]。原因是雷阵雨能否出现的一个关键因素是气块能否被加热抬升至对流凝结高度:当太阳短波辐射被地表吸收后,如下垫面较湿则这部分热能用来蒸发(即转化为潜热),而不加热上面的空气,使气块不易被加热上升达到对流凝结高度而产生对流降水;反之,下垫面较干时,地面通过长波辐射加热上面的空气(即转化为感热),使气块上升达到对流凝结高度而产生对流降水。考虑到目前模式中所用的土壤湿度资料精度很低即不确定度很大,所以对土壤湿度初值进行扰动的集合预报可以较好地模拟夏天雷阵雨降水以及近地面气温预报的不确定性或可能的预报误差。
由于计算机运算速度的限制,在实际的业务集合数值预报中集合成员数不能太多,否则模式分辨率就会过低,因此在一定计算机资源下,集合成员数和模式分辨率要有一个合理的配置。早期关于集合成员数的研究表明[15],对于降水集合预报(平均预报和概率预报)一般成员数达到10个左右就基本接近“最大可获得的预报技巧”。但是Du等[15]的结果是基于空间分辨率较粗(80km)用对流参数化方案的数值模式,那么对于基于空间分辨率很细的显式计算云物理模式的集合预报系统呢?最近Clark等[30]的研究结果表明,即使对于这种基于高分辨率(4km)风暴尺度集合预报系统的降水概率预报,10个左右成员似乎也就够了,但同时也指出随着预报时效的延长和模式空间分辨率的增加,要接近“最大可获得的预报技巧”所需的成员数也随之增加。这一结论同Richardson[31]的结论一致:即一个事件可预报性愈低,要达到“最大可获得的预报技巧”所需的集合成员数就愈多。因此,对于一般短期天气预报,在保证一定成员数的情况下(如10个成员),尽量增加模式空间分辨率和应用较完善的物理方案应是提高预报水平的一种较优选择;Clark等的研究[32-33]也证实了这一点:对于降水(对流天气系统)的预报,5(10)个成员4km显式计算云物理模式的小集合预报系统的预报效果较15(30)个成员20km对流参数化物理模式的大集合预报系统好。但对于较长时效的预报如中期和季节的数值预报(可预报性很低),较多的集合成员数则可能会比增加模式空间分辨率更重要[34]。模式的垂直分辨率对降水预报质量的影响也很大[35],但似乎还没人从集合成员数与垂直分辨率的合理分配角度进行过定量的讨论。
2.2 物理和模式扰动
早期集合预报研究的注意力主要集中在初值不确定性上,但后来Brooks等[36]、Mullen等[37]发现集合成员降水预报的发散性对不同的同化系统和不同的物理参数化方案也很敏感。根据这一思路在美国国家气象局国家环境预报中心(NCEP)建立了世界上第一个基于多初值、多模式和多物理的短期区域集合预报业务系统(SREF,http://www.emc.ncep.noaa.gov/mmb/ SREF/SREF.html),它于2000年开始每天运行,并于2001年正式变成业务预报系统[38-39]。实践证明,多物理、多模式方法是对暴雨和其他较难预报的天气要素如雾[40]等行之有效的集合预报方法;这种多物理、多模式集合预报方法对中国南方暴雨的试验[41]和2008年北京奥运会期间的实时试验[42]也证实它是一种行之有效的方法;并且这种方法在当不同的模式具有相反的系统性偏差时效果尤其显著[42]。关于物理扰动同初值扰动相比对集合离散度的相对贡献大小,许多研究结果都看到物理扰动的贡献似乎是第二位的[43-44],这对降水以外的其他大气变量如温、压、湿、风场更是如此(对于降水预报,有时它们的作用可以相当;对于小尺度的强降水,物理扰动的作用甚至可以超过初值扰动),大尺度的集合离散度可仅通过初值扰动而得到,而物理扰动仅对风暴附近局部地区离散度场在强度如降水量和结构上可有较大的修改作用。打个比方,初值扰动决定了一幅肖像画中人的大致轮廓,而物理扰动则可修改人的五官位置和形状。考虑到天气尺度的误差增长进入非线性阶段大约需1d左右的时间[45],对于降水而言,一般认为在前24h预报中物理扰动的作用较大,而24h以后初值和侧边界扰动会起主要作用。但Clark等[46]的研究表明,即使在前24h,初值和侧边界扰动对降水预报也可能起主导作用。Stensrud等[47]进一步指出,在强天气尺度强迫形势下(如锋面降水),物理扰动相比初值扰动作用较小,而在弱的大尺度强迫背景下(如纯热对流降水),物理扰动作用较初值扰动作用更大或相当。
虽然多模式和多物理的扰动方法实际效果较佳,但鉴于在一个数值预报中心发展和维护多个模式和多种物理方案并不易,因此它不是一种经济的最佳选择。所以,近年来,随机物理扰动方法的发展和研究变得比较热门[48-55]。虽然从文献中可以看到一些正面结果的报告(主要是“离散度—预报技巧关系”有所改进),但根据我们自己正在进行的研究看到这一方法目前并不成熟,其产生的集合离散度远远小于初值扰动或多物理方案或多模式技术所产生的离散度(随机动能后向散射
SKEB法[52]可能是个例外),虽然它在局部地区可以较大幅度地改变降水量,但对模拟降水位置的不确定性几乎无能为力;可喜的是对小尺度预报误差的模拟,随机物理扰动的作用可与初值扰动相当(这对风暴尺度的局地强降水非常重要),另外,如果在初值扰动基础上叠加随机物理扰动,则其综合集合预报结果对最终暴雨预报不确定性的模拟有所改进[56]。
鉴于物理过程的重要性、复杂性以及物理扰动与初值扰动的相互作用等[57-59],如果在一个集合预报系统中不全面包括物理过程的误差源,该集合系统就不可能准确地模拟出局地性很强的所有天气的预报误差分布。如Du[60]在一项研究中发现,只要所用模式有误差,即使在一个集合预报系统中对初值扰动的表征很准确,基于该集合的预报概率密度的分布总会在少数一些地域完全错误,并且很难预测这些错误分布会出现在什么地方,这些少数地域称为“不可预报点”。因此,作者认为今后需进一步深入研发新的、较全面的、较有效的随机物理扰动方法(SKEB方法是否真的有效,还有待进一步证实);也有人对物理扰动方法比较乐观,认为各种物理扰动方法都差不多,所以简单的物理扰动方法在实践中就够用了[61]。我们认为衡量随机物理过程扰动方法是否成功的一个重要指标是它能否有效地复制现行的多模式和多物理扰动法的效果,要实现这一点在目前看来似乎还比较困难。对于模式中的许多误差源,我们现在还不完全了解,有些虽知道但还没有完全认识和应用,如模式地形和实际地形有很大的差异,所以扰动模式地形对暴雨集合预报应该有较显著的影响,这些都需要做进一步的工作。
2.3 模式和资料同化
活跃的对流系统和局地地形往往是造成强降水的直接原因,要准确地预报这些对流系统以及它们与地形的相互作用来模拟这种暴雨过程,基于显式云物理高分辨率(<5km)模式的风暴尺度集合预报是必需的,这在2009年8月登陆台湾的强台风莫拉克(Morakot)造成的台风特大暴雨和2012年7月21日北京的特大暴雨这些历史性事件的研究中得到了很好的体现[18,62]。不用高分辨率模式,这些重大天气过程的细节都不能被准确地描绘出来;这些研究也看到,除了应用显式云物理的高分辨率模式以外,资料同化技术也是关健:譬如,当采用直接同集合预报系统耦合由集合成员来提供与气流相关的背景误差估计场的集合卡尔曼滤波(EnKF)技术[63-66]所产生的分析场作为模式初值时就能较好地预报莫拉克台风暴雨,反之如采用三维变分同化法所产生的分析场作为初值则不能很好地预报这次台风的强降水[18]。
区域集合预报系统需要由更大区域的或全球的集合预报系统来提供侧边界条件,有时也直接提供初始条件。在模式区域较大时,来自侧边界的影响相对较小;但当区域较小时,对集合预报的离散度影响巨大[67]。鉴于计算机资料的限制,目前高分辨率(<5km)显式云物理模式的风暴尺度集合预报区域都比较小,因此侧边界条件影响很大。因为许多数值预报中心自己并不直接运行一个区域较大的“中间分辨率”区域集合预报,所以一个实际问题就是对显式云物理的风暴尺度(<5km)集合预报系统其侧边界和初值是否可以直接由较低分辨率(目前一般为30~50km)的全球集合预报系统来提供而不影响预报质量,或还需要在这两者之间有一个起过渡或桥梁作用的基于参数化物理模式的“中间尺度”区域集合预报系统先把全球粗网格资料进行降尺度。Marsigli等[68]最近对此问题用一个2.8km显式云物理模式的风暴集合预报系统进行了比较:一是用32km欧洲中期气象预报中心的全球集合预报来“直接”驱动(提供侧边界和初值条件)这2.8km风暴尺度集合系统,二是先把32km全球资料用一个7km参数化云物理的区域集合预报进行降尺度再“间接”地驱动这2.8km风暴尺度集合系统。结果发现:(1)对于500hPa高度场,两者预报差异都在集合预报的离散度之内而不明显;(2)对于降水预报,两者在12~45km的空间尺度上有不能忽略的明显差异,显然这对局地的强降水预报会有影响;虽然如此,但他们发现降水预报的技巧两者却没有明显区别。因此,他们认为用32km全球集合预报来直接驱动2.8km显式云物理模式的风暴尺度集合预报似乎是可行的。当然,这个工作还很初步,今后应有更系统的研究来跟进特别是对强对流降水的影响。
2.4 各种替代法产生的“虚拟”集合预报
在没有足够计算机资源来运行你理想中的真正意义上的集合预报系统时,为了能定量估计预报不确定性,许多研究人员提出了各种各样的替代办法来帮助实现这一梦想。时间滞后法[69]和“穷人”集合法[70]是较早时期提出的此类方法的两个代表。时间滞后法(time-lagged ensemble)就是把起始时间不同但终止时间相同的同一个模式所产生的所有预报集合起来,这方法的缺点是不同长度时效的预报质量不一样,所以在制作集合产品时要对不同成员采用不同的权重,其长处是应用了过去不同时刻模式初值的信息。
“穷人”集合法(poor-man ensemble)是因自己不能运行模式而简单地把能获得的众多来源不同的别
的模式预报集合在一起,其坏处也是模式质量不一,所以对不同成员需要采用不同的权重来产生集合预报产品,长处是导致预报不确定的误差源的表征比较全面,因为它考虑了不同的初值和同化系统、不同的物理和模式的动力框架等,所以集合离散度会较大,并且各成员系统性偏差会不一样,因此在集合平均过程中往往会互相抵消而使平均预报非常出色[42]。大家所熟知的“超级集合预报”[71]概念其实就是“穷人”集合法加上对每一成员的统计订正(多元线性回归),并且它的最后产品是一个单一值决定论的预报而并不是概率预报,所以最早的“超级集合预报”并不是现在真正意义上的集合预报,名称有些误导,可能称之为“多模式的统计回归法”更合适。
2004年作者也提出了“双分辨率混合集合预报法(dural-resolution hybrid ensembling)”[72],前提是有一个高分辨率的单一预报和一个低分辨率的集合预报,原理是把两者结合起来各取其精华——基础预报由高分辨率提供(比较精确)而预报不确定性信息由低分辨率集合预报提供(计算机资源允许)来产生一个新的“虚拟”高分辨率集合预报。具体做法是,把低精度集合预报每个成员分解为两部分:控制预报和预报扰动(即扰动成员与控制预报之差),再把预报扰动叠加到高精度单一预报上来产生新的集合成员,也就是用高精度预报来代替原低精度控制预报再还原为集合预报。叠加办法可用“单边法”,即只加,这样保持成员数和原集合一样;也可用“双边法”,即亦加亦减,这使成员数比原集合增加一倍。此法的优点是利用了高分辨率模式的长处(如对暴雨雨量预报较准确),使原集合预报准确率提高,同时又保留了集合预报的不确定性信息;可能的缺点是因为预报扰动部分和基础预报部分来自不同分辨率的模式预报,有可能导致天气系统在时空位置上的不匹配。但作者的实践经验表明,只要高、低精度预报所用的模式相同,预报时效不太长(如<3d),这一不匹配问题似乎不明显。该法已在美国国家环境预报中心的区域和全球集合预报业务中运行多年:在区域集合预报上把21个成员的16km北美区域短期集合预报系统嫁接到基于2个4km-WRF(NCEP NMM和NCAR ARW)模式的几个小区域单一预报上,结合产生一个具有44个成员、2天预报时效和多区域(美东、美西、阿拉斯加、夏威夷和波多黎各)的风暴尺度集合预报,这对于改正强降水雨量和近地面风场预报有较大的帮助;在全球集合预报上把55km的全球集合预报系统GEFS同27km的单一全球预报系统GFS相结合,考虑到高精度预报比低精度预报的优势随着预报时效的延伸而递减,在两者结合的过程中应用了一个权重函数,它从预报起始的1.0(即完全用高精度GFS作为基础预报)逐渐随预报时间的延长而下降,至第5天降为0(即完全用原来低精度的GEFS)。这样混合集合后,也大大地改进了原有全球集合预报的效果。

图1 在高分辨率(1km)模式降水预报中,用“相邻格点法”通过增尺度(a)来产生A点降水概率预报和平均预报(b)的示意图
不久前,Schwartz等[73]针对高分辨率模式虽然在降水量级预报较好,但在具体位置上有很大的不确定性,而试验了一种所谓“邻居法”(neighborhood approach,或较确切地应称为“相邻格点法”)通过增尺度来估计预报的不确定性来产生降水概率预报(也可产生集合平均预报)。具体来说(图1),在一个预先设定的空间尺度范围内(认为模式对小于此尺度的预报没有确定性技巧而不可在确定论的意义上
相信)所有模式格点的值组成一个集合预报,根据这些格点的值来计算出代表中心点的降水概率和集合平均。图1a中模式的原始分辨率为1km,但认为模式对小于6km的降水没有确定预报技巧;所以,通过一个6km的范围(图1a)来计算A点的降水概率和集合平均降水(图1b)。这样可以把单一模式预报转化为概率预报,也可把只有少量成员的小集合预报变成一个成员较多的大集合预报。此法的原理是增尺度(通过增尺度来增加预报的可靠性),关键是如何根据实际问题(模式的预报能力)来确定一个合理的增尺度半经(如图1的例子是3km)。注意,虽然一个模式在小于某一空间或时间尺度下也许没有确定论意义上的预报技巧,但它可以有统计意义上的预报技巧,所以为了充分利用精细的物理方案或地形资讯等原因,完全有理由在小于此尺度的分辨率下运行此模式。
3 预报方法
3.1 集合异常预报法
对罕见极端高影响天气,即使一个模式有能力来预报它,其数值预报也至少有以下两大难点:一是有多大把握所预报的天气确是极端事件?二是其具体的定时、定量、定点预报稳定可靠吗?杜钧等[74]通过对2012年北京7月21日特大暴雨事件的分析显示,集合预报以及它和气候资料相结合的“集合异常预报法”可以提供比单一模式预报更可靠和更准确的信息,从而有效地缓解上述两大难点来大大地提高重大灾害性天气的预报能力。此法的具体步骤如下,通过计算“标准化异常度”(公式1)把数值模式预报同气候资料相比较(图2),可以判断所预报的事件是否是罕见的极端事件,一般其绝对值超过3(即同气候平均之差超过气候标准差三倍)往往为极端事件的表征;并进一步同集合预报相结合,计算集合中每一个成员的“标准化异常度”就可导出某一等级的极端事件出现的概率大小或其预报的可信度。根据这一可信度来增加或减弱预报员对该预报的信心,就可有效地提高对罕见极端高影响天气预报的可靠性。结合天气事件的异常度(代表天气影响的大小)和异常预报的概率(代表预报的可信度)还可导出一个二维定量的灾害性天气预报“社会影响矩阵”;它综合考虑了天气的影响度和预报的可信度,定量地表示某一灾害性天气预报的可能潜在社会影响大小,这无疑比现在的单一确定性预报更科学。他们的研究也看到,从大尺度形势来说,北京“7·21”大暴雨事件的大尺度环境相当典型,是一次可预报性很高的事件,现在的数值预报模式已有能力在近6天前做出大致的预测,但问题是在具体细节方面如降水落区位置、量级以及起止时间在后续预报中存在很大的不确定性,其可预报性却很低,表现在单一模式前后不同时效的细节预报无论在空间位置上还是在强度上都存在很大的跳跃性或不连续性,这使单一模式预报的应用价值大打折扣,因为预报员不知如何适从。然而,他们发现基于集合预报特别是多模式集合的预报,如集合平均和概率预报则可提供更可靠或更连惯的细节预报从而大大地提高预报的应用价值;不但如此,集合预报还可较单一模式预报延长实际可预报性的时效,如在北京“7·21”事件中北京地区量级超过100mm大暴雨的实际可预报性时效提前了2天。
任一天气要素的“标准化异常度”或S A(Standardized Anomaly)可定义如下:

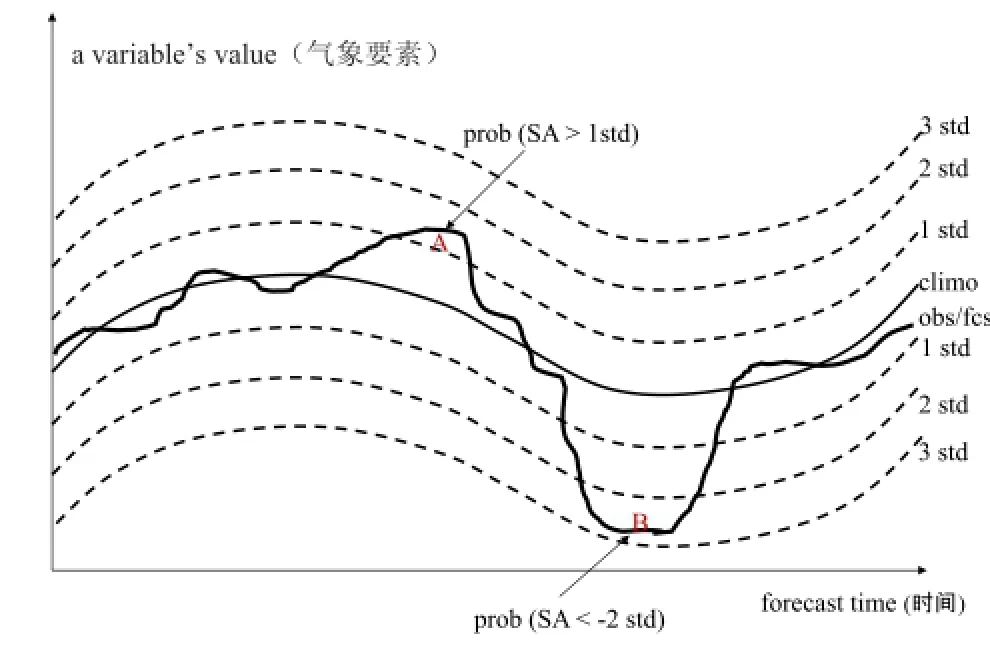
图2 “标准化异常度”方法的示意图[74]:把一个预报或观测的气象要素(粗黑线)同其长期的气候平均(细黑线)和标准差(虚线)进行比较,来衡量该要素的异常度,即用偏离气候平均达多少个标准差来表示
即SA(x,t)就是度量预报值FCST(x,t)超过或低于实际大气的气候平均值MEAN_clim(x,t)达几个气候标准差SD_clim(x,t),标准化异常度SA是地点x和时间t的函数。注意,如果预报有很强的系统性偏差,SA就有可能会高估或低估异常度的倾向。所以,在计算SA前,最好对原始的预报资料先进行偏差订正。关于“集合异常预报法”的详细讨论请参阅文献[74],该文献同时还简单地介绍了一种类似的,被ECMWF采用的“极端预报指数”(Extreme Forecast Index,EFI)方法。
3.2 再预报相似集合预报法
Hamill等[75-76]利用“再预报”(reforecasting)的资料从中找相似,再基于集合预报的思想和表达方法来做暴雨预报。此法的具体步骤和原理如下,首先是
再预报,用最新的业务数值模式(以保证再预报和业务所用的模式一致)利用再分析资料作为初值回算过去一段时期(如过去30年)的每日模式预报以建立一个“过去预报的资料库”(这一步需要大量的计算机资源),这种回算至少是一个成员(即集合控制预报),一般再加几个集合扰动成员一起回算,这既可增加样本数也考虑了初值或物理的不确定性;二是找相似,针对“当前的模式预报”如暴雨事件对每一模式格点在过去再预报资料库中的前后5天(30年×11天×N集合成员数=330N样本数,N最少等于1;在下面的“大气河流”试验中N=11)逐点找相似(如降水量级相似);第三,在所有挑选出的相似预报中,用“对应的实况”来代替预报作为新的预报值,组成新的由实况组成的集合预报(其集合成员数随相似度的要求而异);最后,用所有相似预报对应的实况所组成的新集合成员来计算每一格点上降水超过某一阈值,如50mm的概率以及集合平均等预报产品。从上可见,实施此法需有三套资料:当前单一或集合的模式预报、过去单一或集合的再预报资料,以及过去观测资料。再预报相似集合法的长处有以下两点:一是通过用实况代替模式预报自动订正了模式的误差如模式的系统性偏差,所以对模式要求较低,即使模式不完全有预报能力,也有可能得到有用的预报信息,如此法对中期预报效果尤其明显(见下面“大气河流”试验的例子)就是因为模式对中期预报的可预报性较低;二是考虑了预报的不确定性或可预报性(用概率来表达)。此法的不足是在找相似的过程中没有直接考虑时空结构的相似,但这一点在实际应用中似乎并没有构成问题,可能是因为:(1)在时间上做了前后5天的限定,所以对应的天气系统不至于太离谱(如冷锋降水对应台风降水);(2)在具体个例预报中,模式预报和实况在空间上都自动具有有物理意义的自相关空间结构,如某一种天气系统并不是随机的。另外,相似度的选取有一定的任意性。
全球中期集合预报系统的再预报资料库已在美国国家环境预报中心的业务预报中投入使用[77],但因受计算机资源的限制(另外,一般也认为再预报资料对短期预报的效果可能没有像对中期预报的效果那么明显和必需),还没有在区域短期集合预报模式上开展。由NCEP“天气预报中心”(Weather Prediction Center,WPC)主持,在2012年开展的“大气河流”(Atmospheric River)试验中对“再预报相似集合预报法”和“多模式集合法”进行了对比试验,试验证明再预报相似集合预报法对于中期暴雨预报(3~6天,>75mm/24h)效果较佳,明显优于基于多模式的中期TIGGE①TIGGE (the THORPEX Interactive Grand Global Ensemble) : THORPEX(The Observing System Research and Predictability Experiment)是世界气象组织(WMO)世界天气研究计划(WWRP)中的一个研究项目: http://www.wmo.int/pages/prog/arep/wwrp/new/thorpex_new.html集合预报(由美国国家环境预报中心20个成员GEFS、加拿大气象中心20个成员CMCE和欧洲中期气象预报中心51个成员ECENS,三个全球模式集合系统合成):在8次同大气河流现象相关、发生在美国西海岸的大暴雨事件中(其中故意选了一次没有达到>75mm/24h标准的“虚假”事件),结果发现对于提前3.5天的预报再预报法有7次优于多模式法,只有在那一次“虚假”事件中因空报(实际上是雨量报得不够大)而变差;对于提前5.5天的预报,再预报法在6次事件中比多模式法有明显改进,1次平手(“虚假”事件),仅1次略差。图3(3.5天预报)和图4(5.5天预报)给出其中2011年1月17日的例子:所有三家单独集合预报系统(GEFS、CMCE和ECENS)以及它们合成的多模式集合预报(ARENS)外加一个3.5天预报时效的7km区域集合预报系统(HMT-ENS)全部漏报了发生于华盛顿州和俄勒冈州西部的6块主要暴雨日雨量超过约75mm的雨量中心区(斜线阴影区),只有加拿大气象中心的集合预报CMCE在5.5天预报中对华盛顿州西北部的一个雨量中心略有反映,但却明显空报了位于俄勒冈州和加利福尼亚州相交处的一大片暴雨中心(图4b);而基于再预报相似的集合预报(Reforecast)在4天(比其他模式预报时效多半天)预报中对此6个暴雨中心都有反映(概率1%~15%,图3e),在6天预报中也对其中5个暴雨中心有反映(图4e),当然它也空报了位于俄州和加州相交处的暴雨中心。试验结果看到再预报相似集合预报法的一个缺陷可能是会出现空报现象,但对于可预报性很低的事件如中期暴雨预报,空报现象在科学上是可以理解和应该预见的;在实践中,对重大灾害性天气漏报造成的危害可能远远大于空报。再预报相似集合法在这个试验中明显优于多模式集合法的原因可能是目前的数值预报模式对于中期暴雨预报水平还不高[78],待以后模式进一步改进,基于集合预报系统的中期暴雨预报水平也会相应提高。但是即使到那个时候,3.1节讨论的预报不确定性问题仍将永远存在,集合预报也因此将永远是预报暴雨的必需途径来处理这预报不确定性的科学事实。
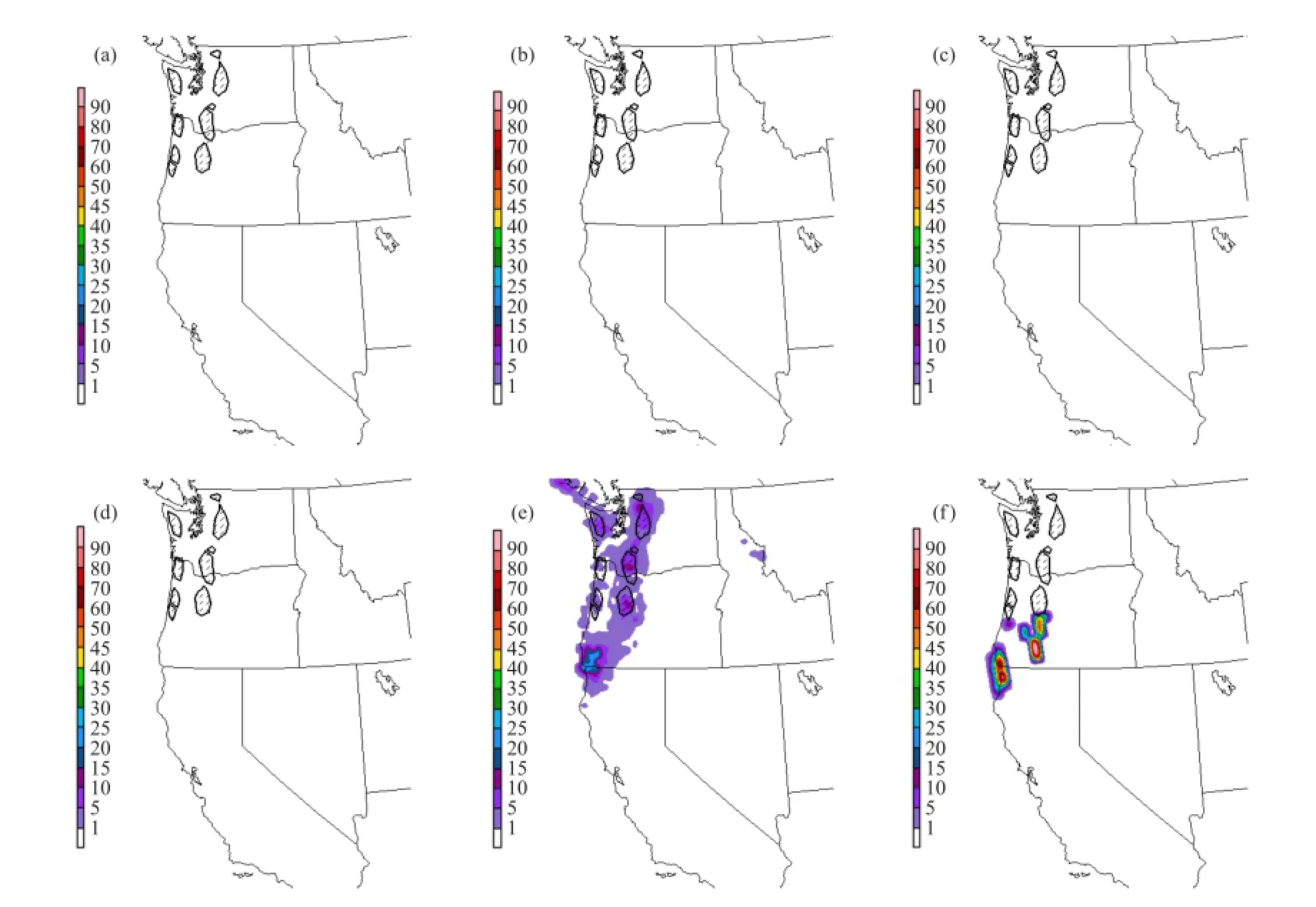
图3 “再预报相似集合预报法”和“多模式集合法”的对比试验(个例:2011年1月16日00z-17日00z美国西海岸大暴雨),实况(斜线阴影区):6块主要暴雨雨量超过75mm/24h的雨量中心区位于华盛顿州和俄勒冈州西部;提前3.5天的“雨量超过75mm/24h”概率预报(颜色):美国国家环境预报中心GEFS(a)、加拿大气象中心CMCE(b)、欧洲中期天气预报中心ECENS(c)、多模式GEFS/CMCE/ECENS合成集合预报ARENS(d)、再预报相似集合预报法Reforecast(提前4天,e)、7km区域集合预报系统HMT-ENS(f)
丑纪范等[79-82]也提出过类似的思想,认为未来的天气事件总可在历史时期找到相似的信息,因此可以利用过去的相似信息作为预测将来之用以弥补数值预报中模式初值信息之不足。当然,再预报相似集合预报法不仅考虑了初值的不足,同时也考虑了物理的不足以及其他各种限制可预报性的因素并且进一步把这些预报不确定性在最后预报产品中定量地表达出来。
3.3 台风路径聚类法
通过对集合预报成员台风路径进行聚类分析来提高台风暴雨的预报服务水平是台湾“中央气象局”应用集合预报的一种方法①洪景山,个人交流。由于台湾岛中央山脉的存在,地形抬升机制对降水的增幅作用明显,因此台风路径的少许差异使气流与山脉的夹角不一样所造成的暴雨降水量相差巨大。所以,他们对集合成员(也包括所有能获得的单一确定预报)以不同的路径,特别是准备对外发布的最佳路径来进行聚类,然后再根据路径(位置)类似的成员(不管该预报的原来预报时效)分类制作不同的暴雨预报以备在不同台风路径(位置)情形下使用。针对受地形强烈影响的台湾地区台风暴雨情形,Fang等[83]进一步提出了用双分辨率的集合预报系统来预报台风暴雨,此法的基本前提是:低分辨率模式的集合预报成员一般都大大地低估暴雨降水量,而因计算机资料的限制用高分辨率模式做集合预报又不能有很多集合成员,但要可靠地用集合预报系统来估计台风的路径和降水的空间分布却需要有足够多的集合成员,因此他们设计了双分辨率的集合预报系统:36km低分辨率的集合预报有32个成员,而4km高分辨率的集合预报仅仅有8个成员。这样用低分辨率的众多集合成员来估计最有可能的台风路径(集合平均)以及用同集合平均路径(位置)相近的成员来估计暴雨分布的空间结构,再用高分辨率集合成员来调整暴雨雨量预报(具体如何调整,请参阅第4节)。类似这些方法,在其他地区特别是山地暴雨的研究和预报应该都适用。
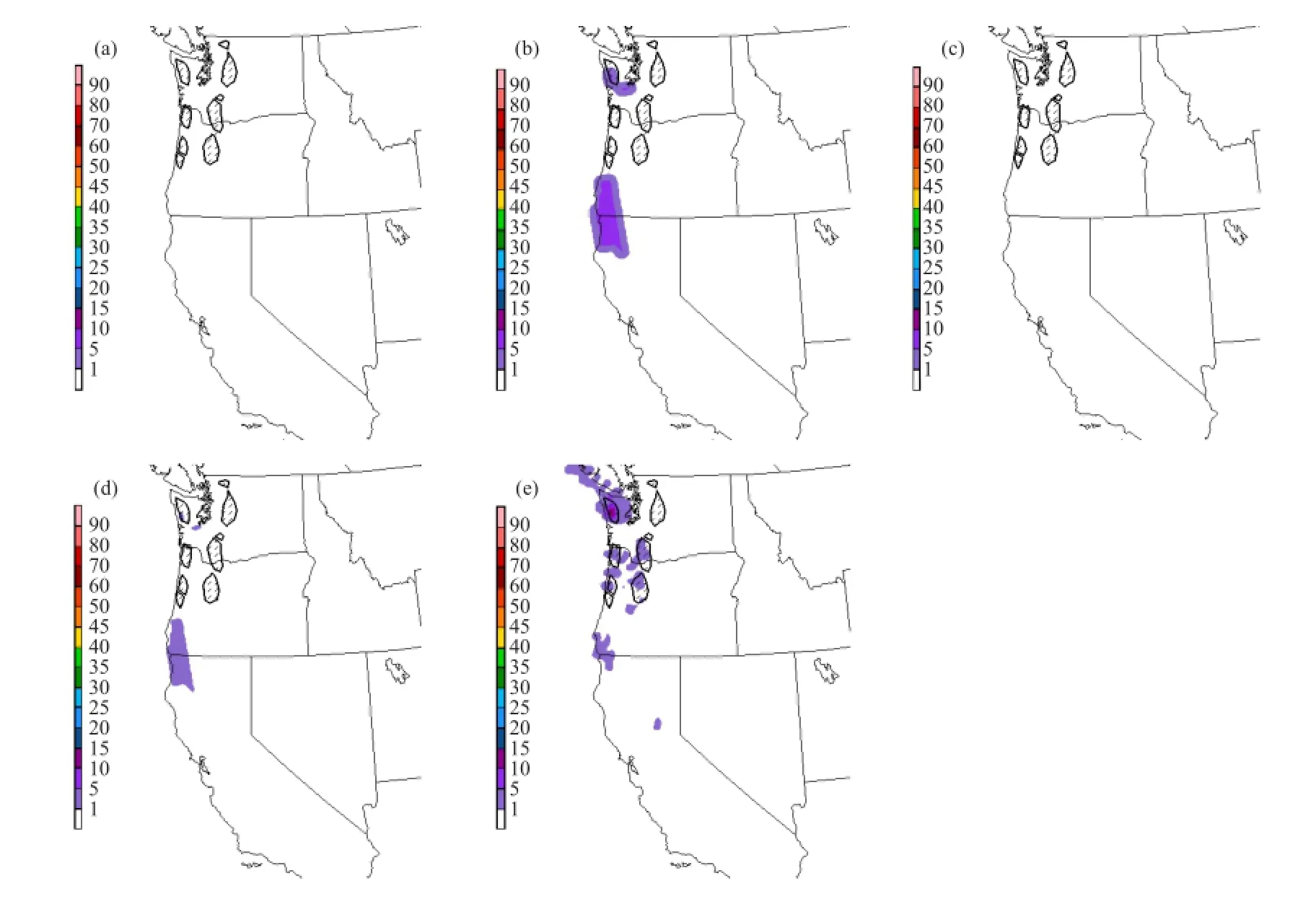
图4 同图3,但是提前5.5天的预报并且没有7km的区域集合预报HMT-ENS
4 用集合预报做暴雨预报的订正
利用集合预报信息,还可以用来订正单一值预报。一般而言,由于集合平均过程的非线性过滤作用把成员中可预报性较低的成分过滤掉而留下各成员共有的信息,因此集合平均预报往往比单个预报更准确(这儿也有平滑造成的虚假贡献。对同一预报而言,一个比较平滑的场比一个具有许多细小结构的场评分要好,因为细小结构很容易报错而在定量评比中不利)。但这一结论往往不完全适用于降水预报,正如Du等[15]的早期研究中指出虽然平均后降水位置可能变得比较准确,但集合平均往往使小降水区扩张过大而大降水区缩减过小,这一问题当集合离散度愈大时(如预报时效愈长和多模式集合)就愈严重。因此简单的集合平均并不适合做降水预报尤其是对很强或很弱两端的降水(最合适的表达应该是用概率)。用集合中值预报来代替集合平均预报可以稍微缓解这一问题但不能彻底解决这一缺陷。Du等[16]提出了一种预估成员相对优劣的方法(称之为“杜—周排序法”)来选取最佳成员或进行加权平均等,方法的原理是:如果模式没有系统性的偏差,集合成员预报应该围绕在真值的周围,有些上有些下、有些左有些右,那么从理论上来说所有集合成员的平均应该是最靠近真值的,所以愈靠近集合平均的成员就应该愈准确。根据这一原理就可用成员与集合平均之间的相对距离来事先对一个集合预报预估其成员的相对优劣(包括最佳和最差成员)并计算出各成员的相对权重系数(用于计算加权集合平均和调整概率密度函数分布)。如果选择最佳的成员作为单一值预报,这不仅可能使预报准确性得以提高,还可使预报保留细小的空间结构而避免了集合平均带来的光滑;坏处是浪费了其他成员提供的有用信息①为了尽量不浪费其他成员的有用信息而又可采用最佳成员,一个折中的办法是先对集合成员进行聚类,然后在每一分类的子集合中选出最佳的成员作为其代表预报。杜—周排序法不同于其他方法的根本之处是它不需要知道每个成员过去(统计)的表现,而只依赖各成员的现时预报本身,是一种随时、随地域和随气流而变的准动力学办法(但对成员排序的计算方法是静态的)。注意:因为排序过程是相对每一预报时效单独进行的,与前后预报时效没有联系,所以即使同一序号的“成员”(如最佳成员)在前后不同预报时效(尤其是当预报时效较长时)很可能对应不同的集合成员,即在时间上没有连续性,时间上不连续性问题在实际应用中(如用来驱动一个扩散模式或图像放映显示)可能会带来不便。为了保持时间上的连续性,可以尝试一种更具内在联系和动力
意义的方法,就是在模式积分过程中在保持合理的离散度前提下不断让成员向集合平均位置靠拢(nudging members toward ensemble mean),当然具体怎么做需要实际试验;另外,对排序结果进行一些简单合理的调整也能解决这一时间不连续性问题(在集合成员聚类法中就用这种办法使某一类的相似预报解保持时间上的连续性)。Du等[16]应用了大气的一些基本状态变量(风、温、压、湿)而并没有对降水进行研究。上面的讨论看到降水的平均预报并不理想,因此把杜—周排序法直接应用到降水预报场或间接地应用到同降水密切相关的其他变量上而不是降水场本身,是否更有效果需进一步的研究。他们还利用排序法得到的每个成员不同权重对加权集合平均同简单(等权重)集合平均进行比较,发现:(1)当集合成员数愈少(多),加权平均效果愈显著(不显著);(2)当一个集合中成员间的表现相差较大(小)时,加权平均效果愈好(差);(3)一般来说,加权平均较简单平均的改进程度可能有限(<10%),特别当集合成员数足够大时,加权平均可能同简单平均相差无几,因此不能期望过高,而要明显提高集合平均水平,必须要有独立的新信息,如加入一个不同的模式。利用集合成员不同的权重也可调整预报概率分布,这可在以后的研究中试验。
为了彻底解决“集合平均使小降水区过大而大降水区过小”这一缺点,Ebert[70,84]提出了“概率或频率匹配法”来订正集合平均降水预报,原理是保证集合平均预报在不同量级降水出现的频率保持同平均前的原始集合预报出现的频率一致,即使小降水出现频数不增多,大降水出现的频数不减少(图5)。最后的预报由两部分合成:降水的空间分布来自较准确的集合平均,而降水量出现的频率则来自较准确的原始集合各成员预报,具体步骤如图5所示。首先,根据所有格点的降水预报值,分別统计出集合平均预报和原始集合预报(包括所有集合成员)在各降水量级出现的频率分布;然后,比较两者的分布,利用多项式拟合技术求得不同雨量的订正系数(比率),并逐点应用到集合平均预报雨量上,把集合平均预报各降水量级的频率分布调整到原始集合预报的分布(实施的技术方案可参阅文献[85]①顺便指出,如果把一个降水预报的降水量出现频率同观测降水频率相比较,则此法就可应用到降水预报的偏差订正中。李俊等[85]的试验表明此法对预报降水量和降水区面积偏差订正都有很好的效果,但却没有能力来订正预报降水的位置误差)。结果表明,这一方法对于消除虚假的小降水区和增幅雨量被低估的大降水区,尤其是暴雨效果非常好[84-85]。
概率匹配法能提高预报准确性是因为它综合了两种不同预报的优势:即集合平均预报在降水位置上较准确,而原始集合成员在降水量级或各量级降水出现的频率分布比较准确,因此把两者结合起来就得到一个较好的预报;反之,如果没有了这两种优势,那么综合后的预报就不会理想。譬如,受到地形强烈影响的台湾地区台风暴雨就出现这种情形:一方面,因为台风路径的集合离散度在登陆前后往往很大,而受台湾中央山脉的影响使不同台风路径所产生的暴雨雨量相差悬殊,因此简单地包括所有集合成员所产生的平均预报降水位置并不佳;另一方面,原始集合成员的降水量级也或因模式分辨率不够而偏小或因强烈的地形作用而系统性地偏大,因此原始集合预报提供的雨量出现频率分布也不理想。这时,简单地应用概率匹配法所产生的集合平均预报效果并不好。针对这种特殊情况,Fang等[83]通过运行一对双分辨率的集合预报系统(“低分辨率大集合预报”和“高分辨率小集合预报”,见3.3节),在应用概率匹配集合平均法之前先对降水分布位置和降水量进行调整和订正并取得较好效果。具体步骤如下:(1)从低精度原始大集合预报中导出每隔3h的集合平均台风位置,即路径(因为成员多,认为较准确;试验表明台风路径预报对模式分辨率并不是很敏感);(2)对每一固定的平均台风位置,从低精度原始大集合预报中选出所有同这平均台风位置相近的成员(不管原预报时效)重新组成一个新集合(称为低精度新集合),并用这低精度新集合产生相对该台风位置的简单集合平均降水预报(因为成员多,认为其降水的空间分布较合
理);(3)类似地,对应每一低精度新集合成员的台风位置,从高精度原始小集合中挑选出所有同它们位置相近的所有预报(不管原预报时效)也重新组成一个新集合(称为高精度新集合),并从这高精度新集合导出相对某一平均台风位置的简单集合平均降水(鉴于成员较少,其降水空间分布位置需做调整);(4)根据低精度新集合的平均降水,调整高精度新集合平均降水的空间位置分布来期望得到较好的降水位置预报;(5)对高精度新集合每一成员的降水量进行偏差订正得到较好的降水量级发生频率的估计(认为降水量级总体来说是合理的,但部分受地形影响而常被高估的降水需要偏差订正);(6)对降水空间分布被调整过的高精度新集合平均降水与每一个进行过偏差订正的高精度新集合成员应用概率匹配法产生一个新的合成集合(称为高精度新合成集合);(7)最后,从这高精度新合成集合可以产生降水的简单集合平均或概率匹配集合平均以及概率预报等,他们发现经过这样处理的新合成集合,其概率匹配平均降水和简单平均降水的预报技巧差不多(说明前期这些位置调整和降水量偏差订正是有效的),并且都明显优于原来单纯的低精度新集合和单纯的高精度新集合预报。

图5 “概率或频率匹配集合平均法”示意图:用原始集合成员的频率分布(实线)来订正简单集合平均降水预报的频率分布(虚线):下调小降水的频率、上调强降水的频率
“集合动力因子”法是高守亭[86]提出的利用集合概念来诊断和定性描述暴雨落区的一种方法。暴雨是热力和动力过程相互作用的产物,许多描述热力和动力场的物理因子,如广义湿位温、水汽通量散度、对流涡度矢量垂直分量及质量垂直螺旋度等都应该在暴雨区有明显反映。但考虑到在不同类型暴雨过程中,这些物理因子的反映可能有差异,所以仅仅用某一物理因子来描述暴雨落区并不可靠;而利用多个因子(集合)共同给出的综合结果则会比较稳定可靠。这种方法对于诊断和定性描述暴雨落区,如台风暴雨和四川低涡暴雨确实有很好的对应关系[87-88]。科学的价值在于预测未来,下面从预报的角度来分析一下此法的优缺点和可能的潜力。首先,此法并不是一种独立的预报方法而是数值模式的直接输出结果(如同常见的对流有效位能、气块抬升指数、涡度、散度等诊断量一样),所以其结果好坏依赖于模式的质量;第二,此法只能定性地指出暴雨可能范围或强降水落区等,而并不能定量地预报雨量;第三,为了更好地区别应用这些因子,需要仔细分析哪些物理因子是果(暴雨本身的反映),哪些物理因子是因(造成暴雨)以及它们超前反映(提前暴雨)的时间长短,如它只是暴雨本身的反映,那么它可用来描述暴雨过程,但其预报的功能就有限,而那些造成暴雨的物理因子其预报的价值可能会更大,所以需要一个描述这些物理因子的清单;第四,鉴于目前的数值预报模式已能直接预报暴雨,并且不管在落区还是雨量上已有相当的能力,所以在暴雨落区预报上来定量地比较集合动力因子法是否优于当前业务模式的直接预报是一项首先应该做的调查[89];最后,如果并不明显优于数值暴雨预报,此法是否可以用作订正模式预报之用?譬如目前高分辨率的显式云物理模式常常有许多虚假的小区域风暴降水或漏报一些局地性的强降水,那么此法能否预先指出模式空报、漏报之处或用来帮助校准暴雨中心的位置等,此法用于订正模式暴雨预报是一项有实际意义的,应该做进一步研究的工作。顺便指出,集合动力因子法只是利用了集合的概念而并不是第2节中所讨论的真正意义上的集合预报。
5 应用集合预报研究天气系统发展机理和指导目标观测
集合预报成员的离散度不但可以定量描述预报的不确定度以增加预报信息来提高气象服务质量,而且还可分析天气系统为何发展与不发展的热力和动力原因,进一步利用集合敏感性[90-91]等工具还可帮助预报员了解为什么某一天气系统不好预报的上游原因,并可指导下一步的目标观测[92-93],以改进下一时刻数值模式的初值质量来提高对该天气系统后续预报的可预报性[14]。另一个应用集合预报离散度信息来改进模式初值的途经是通过集合预报系统与资料同化系统的直接耦合,这已在第2.3节讨论过,在此不再重复。
作者[17]利用中国气象局武汉暴雨研究所的区域集合预报系统[21,26,94],对常造成长江、黄河中下游地区大暴雨的主要天气系统西南涡进行了集合分析,通过分析“东移”和“滞留”两组集合成员的模式初值扰动结构,看到东移和不东移的西南涡在热力场和动力场结构上的系统性差异,这些有利于西南涡东移的特征结构和以前他人通过观测分析、数值试验等其他手段所揭示的特征是一致的。这说明集合预报资料确实可以被用来正确地了解一个天气系统发展与否的机理。这种直接利用集合预报成员的不同表现来研究天气系统的机理给我们开拓了一个崭新的研究方法(可称之为“即时研究”,real-time research),因为它不同于传统的“观测研究”(需要有包含众多相似个例①但这些个例间只是大致相似而已,它们所处的大尺度环流背景其实还是有很大的差别,但这对集合各成员来说却并不是问题(即具有完全一致的大尺度环流背景)的特殊观测资料)
和“数值模拟研究”(需要专门设计和进行初值或物理的敏感性试验等),它不需要事先专门的试验设计而只要利用每天可获得的现成的业务集合数值预报资料就可即时对你感兴趣的个例分析为什么有些成员报得“好”,而另外一些成员报得“不好”的可能因素,这对广大业务预报人员来说是一种唾手可得的方法。更具深远意义的是,我们的研究表明借用仅仅基于相关系数的简单“集合敏感性”工具[90](而不一定需要复杂的手段,如奇异矢量法)就可以根据集合预报的离散度帮助“目标观测”在上游地区找到有效的“预报误差敏感区”,并通过略微“改进”敏感区内的风场或水汽场的初值就可大大地改进西南涡的短期数值预报。鉴于此,建议应该以针对改进西南涡预报为目的,开展用中尺度区域集合预报结合集合敏感性方法来指导的实际“目标观测”野外试验,来验证实际目标观测对西南涡短期数值预报改进的效果是否同该研究模拟的一样。如是,无疑将对改进东移西南涡造成的暴雨预报有巨大的实际意义并可在实际业务中应用。
在中期数值预报上,为了提高中高纬气旋风暴的可预报性,集合预报用来指导目标观测中应在上游何处进行加密气象观测已是美国气象局业务数值预报的一部分[95-96]。这种中期预报(如美国东海岸冬季的爆发性气旋)的预报误差敏感区常常同上游(如日本上空)急流区的Rossby波包有关[97-98](即下游效应[99])。陶诗言等[100]也发现欧亚上空急流区的Rossby波同中国的高影响天气如华北深槽暴雨或北上台风暴雨等有密切的关系。这种关系在目前的全球中期数值模式预报中已大致可提前1周甚至更长时间被预报出来,但难处是其下游产生的气旋强度和位置却有非常大的不确定性(其实在1~3天的短期预报也是如此)。所以事先有目的地通过目标观测手段对上游敏感区进行加密观测来尽量减少模式初值中对Rossby波包的描述误差从而提高后续中高纬气旋风暴强度和位置预报的准确性是一种主动有效的科学手段。在此新领域,集合预报方法有着其他决定论方法无可比拟的优势。类似地,Zheng等[91]利用全球集合预报资料,通过计算集合敏感性试图提供一个让预报员来了解气旋位置和强度预报不确定性来源的工具。
6 总结和讨论
本文根据作者自己多年的研究和实践经验以及直接接触的一些研究和方法,简要地总结了数值集合预报方法在暴雨研究和预报中的应用,这包括以下几个方面:暴雨集合预报系统、预报方法、预报后处理与订正,以及暴雨天气系统的机理分析与模式初值的改进。
(1)在集合预报系统发展方面,建立高分辨率(1~3km)具有显式云物理的风暴尺度集合预报系统势在必行。从目前结果看,采用基于集合卡尔曼滤波(EnKF)(或集合—变分混合)技术与资料同化系统耦合所产生的初值集合来驱动集合预报效果似乎较佳;但在风暴尺度下现有的初值扰动方法是否适用以及如何改进或创新是一个需要研究的课题,目前的初值扰动主要是针对斜压不稳定的天气尺度系统,如何有效地扰动对流不稳定的中小尺度系统尚需探讨;目前的扰动方法对于短时(<24h)的预报效果似乎也不理想,如其导出的集合预报往往比对应的高精度单一预报差;扰动土壤湿度初值对于改进夏季午后雷阵雨以及近地面气温预报有较好的效果。在模式物理扰动方面,多模式和多物理扰动方法被证实是行之有效的方法,但随机物理过程扰动目前还不成熟,所产生的集合离散度太小(也许SKEB法是个例外),因此需要进一步深入研发新的、较全面有效的随机物理扰动方法,在显式云物理模式中如何引入随机物理过程,是否需要云物理的集合方案或直接扰动云中各种含水量和随机相态过程等,以及认识物理扰动如何同初值扰动相互作用等,这些都需进一步研究。另外,模式地形与实际地形有很大的不同,在暴雨集合预报中应该考虑地形的扰动来模拟由此导致的暴雨误差分布特征。直接用低分辨率的全球集合预报来驱动显式云物理模式的风暴尺度集合预报是否可行还需进一步探讨,特别是对中小尺度对流降水的效果。在有限的计算机资源下,对于一般短期天气预报,在保证一定成员数的情况下(如10个成员),尽量增加模式空间分辨率和应用较完善的物理方案应是提高预报水平的一种较优选择;但对于较长时效的预报如中期和季节的数值预报(可预报性很低),采用较多的集合成员数则可能会比增加模式空间分辨率更重要。在计算机资源不允许的情况下,许多“虚似”的集合预报也可用来有效地定量估计预报的不确定性,文中介绍了时间滞后法、“穷人”集合法、双分辨率混合集合预报法和相邻格点法。
(2)在集合预报方法方面,高影响天气和异常事件的预报是重点。集合异常预报法可明显地提高暴雨特别是异常少见的特大暴雨预报的可靠性;再预报相似集合预报法是动力和统计方法巧妙相结合,在目前模式预报水平还不够好的情况下是对中期暴雨预报水平提高有特殊效果的一种方法;台风路径聚类法
可有效地提高受地形强烈影响的台风暴雨的预报准确性,类似的方法可也用于山地暴雨的预报。
(3)在预报后处理订正方面,对于降水预报要用概率匹配平均来替代简单的集合平均以减少暴雨雨区和雨量的低估,在特殊情形下(如受地形强烈影响的台风暴雨)在应用概率匹配平均法前要对原始集合降水预报进行一些处理;另外,对平均预报和各成员预报还应该进行模式偏差订正。文中还介绍了一种预估集合成员相对优劣的“杜—周排序法”来选取最佳成员或进行加权平均等。“集合动力因子”法用于订正模式暴雨预报可能会有实际意义,应该做进一步研究。除了订正平均值如偏差(反映模式的水平),更要订正集合离散度的分布(反映集合技术的水平),使集合离散度能正确地反映预报的误差(“离散度-预报技巧”关系)和概率预报能可靠地反映预报的真实可信度[14],因为可靠的概率预报是用户决策是否正确的关键[12]。
(4)在研究方法方面,本文介绍了一种直接利用集合预报成员的不同表现来研究天气系统机理的“即时研究”新方法,它对广大业务预报人员来说是一种易得的手段。因此,这对加强业务与科研的互动,加速提高预报水平会有促进作用。
(5)在数值预报总体系统方面,集合预报应该用来指导进行目标观测,通过改进模式初值来提高某些选定的重大天气系统或事件预报的可预报性;为了科学地反映观测和预报的不确定性,集合预报系统还需要与资料同化系统耦合为一个有机的整体。这是数值预报系统(观测—同化—预报—服务)从“单一值、单向”的决定论系统向“多值、交互式”的概率论系统转化所迈出的坚实一步[7]。
通过总结,希望本文能起到如下两个作用:气象业务部门能在日常业务中应用本文介绍的众多行之有效的方法来提高气象预报和服务水平;为今后的研究工作提供一个新的起点、方向和方法,这包括指导现有的一些业务集合预报系统[94,101]今后的进一步完善。虽然讨论了许多方面,但最终目的只有一个,就是向用户提供尽可能详细和全面的气象预报使不同的用户可以充分运用全面的(不是目前这种确定性单一值的、用户无法选择的、不全面的)气象预报信息来选择性地做出最适合自身经济或社会风险承受能力的最佳决策。本文希望能对天气预报从“确定性单一值的不完全预报”向“多选择的包含了不确定性的完全预报”理念转变[10]起到促进作用。
致谢:感谢Thomas Workoff先生帮助绘制图3和图4。
[1]章国材. 防御和减轻气象灾害. 气象, 2006, 32(3): 3-5.
[2]陶诗言, 等. 中国之暴雨. 北京: 科学出版社, 1980.
[3]陈云峰, 高歌. 近20年我国气象灾害损失的初步分析. 气象, 2010, 36(2): 76-80.
[4]张大林. 各种非绝热物理过程在中尺度模式中的作用. 大气科学, 1998, 22(4): 548-561.
[5]Lorenz E N. 混沌的本质 . 刘式达, 刘式适, 严中伟译. 北京: 气象出版社, 1997.
[6]丑纪范. 大气科学中的非线性与复杂性. 北京: 气象出版社, 2002.
[7]杜钧, 陈静. 单一值预报向概率预报转变的基础: 谈谈集合预报及其带来的变革. 气象, 2010, 36(11):1-11.
[8]王东海, 杜钧, 柳崇健. 正确认识和对待天气预报的不确定性. 气象, 2011, 37(4): 385-392.
[9]杜钧, 陈静. 天气预报的公众评价与发布形式的变革. 气象, 2010, 36(1): 1-6.
[10]杜钧, 康志明. 天气预报中不确定性问题的调查分析. 气象科技进展, 2014, 4(1): 58-67.
[11]US National Research Council. Completing the Forecast: Characterizing and Communicating Uncertainty for Better Decision Using Weather and Climate Forecasts. Washington D C:The National Academy Press, 2006.
[12]杜钧, 邓国. 单一值预报向概率预报转变的价值: 谈谈概率预报的检验和应用. 气象, 2010, 36(12): 10-18.
[13]杜钧. 集合预报的现状和前景. 应用气象学报, 2002, 13(1): 16-28.
[14]Du J, Yu R C, Cui C G, et al. Using a mesoscale ensemble to predict forecast error and perform targeted observation. Acta Oceanologica Sinica, 2014, 33(1): 83-91.
[15]Du J, Mullen S L, Sanders F. Short-range ensemble forecasting of quantitative precipitation. Mon Wea Rev, 1997, 125: 2427-2459.
[16]Du J, Zhou B B. A dynamical performance-ranking method for predicting individual ensemble member’s performance and its application to ensemble averaging. Mon Wea Rev, 2011, 129(10): 3284-3303.
[17]Li J, Du J, Zhang D L, et al. Ensemble-based analysis and sensitivity of mesoscale forecasts of a vortex over southwest China. Q J R Meteorol Soc, 2014, 140: 766-782.
[18]Zhang F, Weng Y, Kuo Y H, et al. Predicting typhoon Morakot’s catastrophic rainfall with a convection-permitting mesoscale ensemble system. Weather and Forecasting, 2010, 25: 1816-1825.
[19]Stensrud D J, Brooks H E, Du J, et al. Using ensembles for shortrange forecasting. Mon Wea Rev, 1999, 127: 433-446.
[20]Yuan H, Mullen S L, Gao X, et al. Verification of probabilistic quantitative precipitation forecasts over the southwest United States during winter 2002/03 by the RSM ensemble system. Mon Wea Rev, 2005, 133: 279-294.
[21]李俊, 杜钧, 王明欢, 等. 中尺度暴雨集合预报系统研发中的初值扰动试验. 高原气象, 2009, 28(6): 1365-1375.
[22]陈静, 薛纪善, 颜宏. 一种新型的中尺度暴雨集合预报初值扰动方法研究. 大气科学, 2005, 29(5): 717-726.
[23]Toth Z, Kalnay E. Ensemble forecasting at NMC: The generation of perturbations. Bul Amer Meteor Soc, 1993, 74: 2317-2330.
[24]Toth Z, Kalnay E. Ensemble forecasting at NCEP and the breeding method. Mon Wea Rev, 1997, 125: 3297-3319.
[25]Johnson A, Wang X G, Xue M, et al. Multiscale characteristics and evolution of perturbations for warm season convection-allowing precipitation forecast: Dependence on background flow and method of perturbation. Mon Wea Rev, 2014, 142(3): 1053-1073.
[26]李俊, 杜钧, 王明欢, 等. AREM模式两种初值扰动方案的集合降水预报试验及检验.热带气象学报, 2010, 26(6): 217-228.
[27]Du J, Gayno G, Mitchell K E, et al. Sensitivity study of T2m and precipitation forecasts to soil moisture initial condition using NCEP WRF ensemble system. 22nd Conf on Weather Analysis and Forecasting/18th Conf on Numerical Weather Prediction, 2007, Park City, UT. American Meteor Soc.
[28] Aligo E A, Gallus Jr W A, Segal M. Summer rainfall forecast spread in an ensemble initialized with different soil moisture
analyses. Weather and Forecasting, 2007, 22: 2, 299-314.
[29]Sutton C, Hamill T M, Warner T T. Will perturbing soil moisture improve warm-season ensemble forecasts? A proof of concept. Mon Wea Rev, 2006, 134: 3174-3189.
[30]Clark A J, Kain J S, Stensrud D J, et al. Probabilistic precipitation forecast skill as a function of ensemble size and spatial scale in a convection-allowing ensemble. Mon Wea Rev, 2011, 139: 1410-1418.
[31]Richardson D S. Measures of skill and value of ensemble prediction systems, their interrelationship and the effect of ensemble size. Quart J Roy Meteor Soc, 2001, 127: 2473-2489.
[32] Clark A J, Gallus Jr W A, Xue M, et al. A comparison of precipitation forecast skill between small convection-permitting and large convection-parameterizing ensembles. Wea and Forecasting, 2009, 24: 1121-1140.
[33]Clark A J, Gallus Jr W A, Xue M, et al. Convection-allowing and convection-parameterizing ensemble forecasts of a mesoscale convective vortex and associated severe weather. Wea Forecasting, 2010, 25: 1052-1081.
[34]Ma J H, Zhu Y J, Wobus R, et al. An effective configuration of ensemble size and horizontal resolution for the NCEP GEFS. Adv Atmos Sci, 2012, 29(4): 782-794.
[35] Aligo E A, Gallus Jr W A, Segal M. On the impact of WRF model vertical grid resolution on Midwest summer rainfall forecasts. Weather and Forecasting, 2009, 24: 2, 575-594.
[36]Brooks H E, Tracton M S, Stensrud D J, et al. Short- range ensemble forecasting: Report from a workshop, 25-27 July 1994. Bull Amer Meteorol Soc, 1995, 74: 2317-2330.
[37]Mullen S L, Du J, Sanders F. The Dependence of ensemble dispersion on analysis–forecast systems: Implications to shortrange ensemble forecasting of precipitation. Mon Wea Rev, 1999, 127: 1674-1686.
[38]Du J, Tracton M S. Implementation of a real-time short-range ensemble forecasting system at NCEP: An update. 9th Conference on Mesoscale Processes, 2001, Ft Lauderdale, Florida. Amer Meteor Soc, 355-356. http://www.emc.ncep.noaa.gov/mmb/ SREF/reference.html
[39]Du J, DiMego G, Tracton M S, et al. NCEP short-range ensemble forecasting (SREF) system: multi-IC, multi-model and multiphysics approach. Research Activities in Atmospheric and Oceanic Modelling (edited by J. Cote), Report 33, CAS/JSC Working Group Numerical Experimentation (WGNE), WMO/TD, 2003, No. 1161, 5.09-5.10. http://www.emc.ncep.noaa.gov/mmb/SREF/ reference.html
[40]Zhou B B, Du J. Fog prediction from a multimodel mesoscale ensemble prediction system. Wea and Forecasting, 2010, 25: 303-322.
[41]吴政谦, 徐海明, 王东海, 等. 中尺度多模式超级集合预报对2010年6月19—20日中国南方大暴雨过程的分析. 热带气象学报, 2012(5): 653-663.
[42]Duan Y H, Gong J D, Du J, et al. An overview of the Beijing 2008 Olympics Research and Development Project (B08RDP). Bull Amer Meteor Soc, 2012, 93: 381-403.
[43]Du J, et al. The NOAA/NWS/NCEP Short Range Ensemble Forecast (SREF) system: Evaluation of an initial condition vs multiple model physics ensemble approach. 16thConf on Numerical Weather Prediction/20th Conf on Weather Analysis and Forecasting, Seattle, WA. Amer Meteor Soc, 2004. http://ams. confex.com/ams/pdfpapers/71107.pdf
[44]Kong F Y, et al. Preliminary analysis on the real-time storm-scale ensemble forecasts produced as a part of the NOAA Hazardous Weather Testbed 2007 Spring Experiment. 22nd Conf on Weather Analysis and Forecasting/18th Conf on Numerical Weather Prediction, Park City, UT. Amer Meteor Soc, 2007. http://ams. confex.com/ams/pdfpapers/124667.pdf
[45]Gilmour I, Smith L A, Buizza R. Linear Regime Duration: Is 24 Hours a Long Time in Synoptic Weather Forecasting? J Atmos Sci, 2001, 58: 3525-3539.
[46] Clark A J, Gallus Jr W A, Chen T C. Contributions of mixed physics versus perturbed initial/lateral boundary conditions to ensemble-based precipitation forecast skill. Monthly Weather Review, 2008, 136: 6, 2140-2156.
[47]Stensrud D J, Bao J W, Warner T T. Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems. Mon Wea Rev, 2000, 128: 2077-2107.
[48]Buizza R, Palmer T. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Quart J Roy Meteor Soc., 1999, 125: 2887-2908.
[49]谭燕, 陈德辉. 基于非静力模式物理扰动的中尺度集合预报试验. 应用气象学报, 2007, 18(3): 396-406.
[50]Teixeira J, Reynolds C. Stochastic nature of physical parameterizations in ensemble prediction: A stochastic convection approach. Mon Wea Rev, 2008, 136: 483-496.
[51]Li X, Charron M, Spacek L, et al. A regional ensemble prediction system based on moist targeted singular vectors and stochastic parameter perturbations. Mon Wea Rev, 2008, 136: 443-462.
[52]Berner J, Shutts G J, Leutbecher M, et al. a spectral stochastic kinetic energy backscatter scheme and its impact on flowdependent predictability in the ECMWF ensemble prediction system. J Atmos Sci, 2009, 66: 603-626.
[53]Charron M, Pellerin G, Spacek L, et al. Toward random sampling of model error in the Canadian ensemble prediction system. Mon Wea Rev, 2010, 138: 1877-1901.
[54]Berner J, Ha S Y, Hacker J P, et al. Model uncertainty in a mesoscale ensemble prediction system: Stochastic versus multiphysics representations. Mon Wea Rev, 2011, 139: 1972-1995. [55]Bouttier F, Vié B, Nuissier O, et al. Impact of stochastic physics in a convection-permitting ensemble. Mon Wea Rev, 2012, 140: 11, 3706-3721.
[56]李俊, 杜钧, 刘羽. 北京“7.21”特大暴雨不同集合预报方案的对比试验.气象学报,2014,待发表.
[57]Jankov I, Gallus Jr W A, Segal M, et al. The impact of different WRF model physical parameterizations and their interactions on warm season MCS rainfall. Wea Forecasting, 2005, 20: 1048-1060.
[58]Jankov I, Schultz P J, Anderson C J, et al. The impact of di ff erent physical parameterizations and their interactions on cold season QPF in the American river basin. Journal of Hydrometeorology , 2007, 8(5): 1141-1151.
[59]Jankov I, Gallus Jr W A, Segal M, et al. Influence of initial conditions on the WRF-ARW model QPF response to physical parameterization changes. Weather and Forecasting, 2007, 22(3): 501-519.
[60]Du J. Impact of model error and imperfect initial condition perturbations on ensemble-based probabilistic forecasts: Unpredictable spots. 17th Conference on Numerical Weather Prediction/21st Conference on Weather Analysis and Forecasting, Washington DC, Aug 1-5, 2005, Amer Meteor Soc, 2005. http:// www.emc.ncep.noaa.gov/mmb/SREF/reference.html
[61] LeonciniG, Plant R S, Gray S L, et al. Ensemble forecasts of a flood-producing storm: Comparison of the influence of modelstate perturbations and parameter modi fi cations. Quarterly Journal of the Royal Meteorological Society, 2013, 139 (670): 198-211.
[62]Zhang D L, Lin Y, Zhao P, et al. The Beijing extreme rainfall of 21 July 2012: “Right results” but for wrong reasons. Geophys Res Lett, 2013, 40: 1426-1431.
[63] Houtekamer P L, Mitchell H L. Data assimilation using an ensemble Kalman filter technique. Mon Wea Rev, 1998, 126: 796-811.
[64]Houtekamer P L, Mitchell H L. A sequential ensemble Kalman fi lter for atmospheric data assimilation. Mon Wea Rev, 2001, 129: 123-137.
[65]Anderson J L. An ensemble adjustment Kalman filter for data assimilation. Mon Wea Rev, 2001, 129: 2884-2903.
[66] Evensen G. The ensemble Kalman fi lter: Theoretical formulation and practical implementation. Ocean Dyn, 2003, 53: 343-367.
[67]Du J, Tracton M S. Impact of lateral boundary conditions on regional-model ensemble predicion. In: Ritchie H. Research
Activities in Atmospheric and Oceanic Modelling. Report 28, CAS/JSC Working Group Numerical Experimentation (WGNE), WMO/TD-No. 942, 6.7-6.8, 1999.
[68]Marsigli C A, Montani A, Paccagnella T. Provision of boundary conditions to convection-permitting ensemble: Comparison of two di ff erent approaches. Nonlinear Processes in Geophysics, 2014, 21: 393-403.
[69]Ho ff man R N, Kalney E. Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A, 1983, 35A(2): 100-118.
[70] Ebert E E. Ability of a poor man’s ensemble to predict the probability and distribution of precipitation. Mon Wea Rev, 2001, 129: 2461-2479.
[71]Krishnamurti T N, Kishtawal C M, LaRow T, et al. Improved weather and seasonal climate forecasts from multimodel superensemble. Science, 1999, 285(5433): 1548-1550.
[72]Du J. Hybrid ensemble prediction system: A new ensembling approach. Symposium on the 50th Anniversary of Operational Numerical Weather Prediction, University of Maryland, College Park, Maryland, June 14-17, 2004. Amer Meteor Soc, http://www. emc.ncep.noaa.gov/mmb/SREF/reference.html
[73]Schwartz C S, et al. Toward improved convection-allowing ensembles: Model physics sensitivities and optimizing probabilistic guidance with small ensemble membership. Wea Forecasting, 2010, 25: 263-280.
[74]杜钧, Grumm R H, 邓国. 预报异常极端高影响天气的“集合异常预报法”: 以北京2012.7.21特大暴雨为例. 大气科学, 2014, 38(4): 685-699.
[75]Hamill T M, Whitaker J S, Mullen S L. Reforecasts: An important dataset for improving weather predictions. Bull Amer Meteor Soc, 2006, 87: 33-46.
[76]Hamill T M, Whitaker J S. Probabilistic quantitative precipitation forecasts based on reforecast analogs: Theory and application. Mon Wea Rev, 2006, 134: 3209-3229.
[77]Hamill T M, Bates G T, Whitaker J S, et al. NOAA's secondgeneration global medium-range ensemble reforecast dataset. Bull Amer Meteor Soc, 2013, 94: 1553-1565.
[78]Qian W H, Li J, Shan X L. Application of synoptic-scale anomalous winds predicted by medium-range weather forecast models on the regional heavy rainfall in China in 2010. Science China: Earth Sciences, 2013, doi: 10.1007/s11430-013-4586-5.
[79]丑纪范. 数值天气预报的创新之路——从初值问题到反问题. 气象学报, 2007, 65(5): 673-682.
[80]任宏利, 丑纪范. 统计-动力相结合的相似误差订正法. 气象学报, 2005, 63(6): 988-993.
[81]龚建东, 丑纪范. 论过去资料在数值天气预报中使用的理论和方法. 高原气象, 1999, 18(3): 392-399.
[82]邱崇践, 丑纪范. 天气预报的相似-动力方法. 大气科学, 1989, 13(1): 20-28.
[83]Fang X Q, Kuo Y H. Improving ensemble-based quantitative precipitation forecast for topography-enhanced typhoon heavy rainfall over Taiwan with a modified probability-matching technique. Mon Wea Rev, 2013, 141: 3908-3932.
[84]Ebert E E. Probability-matched ensemble mean. 2001.http:// www.cawcr.gov.au/sta ff/eee/etrap/probmatch.html
[85]李俊, 杜钧, 陈超君. 降水偏差订正的频率(或面积)匹配方法介绍和分析. 气象, 2014, 40(5): 580-588.
[86]高守亭. 大气中尺度运动的动力学基础及预报方法. 北京: 气象出版社, 2007.
[87]王成鑫, 高守亭, 梁莉, 等. 动力因子对地形影响下的四川暴雨落区的诊断分析. 大气科学, 2013, 37(5): 1099-1110.
[88]许娈, 何金海, 高守亭, 等. 集合动力因子对登陆台风“莫拉克”(0908)暴雨落区的诊断与预报研究. 大气科学, 2013, 37(1): 23-35.
[89]冉令坤, 齐彦斌, 郝寿昌. “7·21”暴雨过程动力因子分析和预报研究. 大气科学, 2014, 38(1): 83-100.
[90]Torn R D, Hakim G J. Ensemble-based sensitivity analysis. Mon Wea Rev, 2008, 136, 663-677.
[91]Zheng M H, Chang E K M, Colle B A. Ensemble sensitivity tools for assessing extratropical cyclone intensity and track predictability. Wea and Forecasting, 2013, 28(5): 1133-1156.
[92]Emanuel K, Langland R. FASTEX adaptive observations workshop. Bull Amer Meteor Soc, 1998, 79: 1915-1919.
[93]Langland R H. Issues in targeted observing. Quart J Roy Meteor Soc, 2005, 131: 3409-3425.
[94]李俊, 王明欢, 公颖, 等. AREM短期集合预报系统及其降水预报检验. 暴雨灾害, 2010, 29(1): 30-37.
[95] Toth Z, Szunyogh I, Majumdar S, et al.Targeted observations at NCEP: Toward an operational implementation. 4th Sym Integrated Obs Sys, Amer Meteo Soc, 2000.
[96]Szunyogh I, Toth Z, Morss R C, et al. The effect of targeted dropsonde observations during the 1999 Winter Storm Reconnaissance Program. Mon Wea Rev, 2000, 128: 3520-3537.
[97]Chang E K M, Yu D B. Characteristics of wave packets in the upper troposphere. Part I: Northern Hemisphere winter. J Atmos Sci, 1999, 56: 1708-1728.
[98]Chang E K M. Characteristics of wave packets in the upper troposphere. Part II: Seasonal and hemispheric variations. J Atmos Sci, 1999, 56: 1729-1747.
[99]Yeh T C. On energy dispersion in the atmosphere. J Atmos Sci, 1949, 6: 1-16.
[100]陶诗言, 卫捷, 梁丰,等. Rossby波的下游效应引发我国高影响天气的分析. 气象, 2010, 36(7): 81-93.
[101]邓国, 龚建东, 邓莲堂, 等. 国家级区域集合预报系统研发和性能检验. 应用气象学报, 2010, 21(5): 513-523.
Application of Ensemble Methodology to Heavy-Rain Research and Prediction
Du Jun1, Li Jun2
(1 National Centers for Environmental Prediction (NCEP), National Oceanic and Atmospheric Administration (NOAA), USA 2 Wuhan Institute of Heavy Rain, China Meteorological Administration, Wuhan 430074)
Inability in correctly predicting heavy rain events is primarily due to two reasons: lack of full understanding its physical mechanism and negligence of its predictability limit. How to deal with its predictability limit is the focus of this review paper, which is especially important to enhance the value of numerical weather prediction products to better serve end-users. Based mainly on authors' own or directly involved researches and experiences, many applications of ensemble methodology to heavy rain research and prediction are brief l y overviewed. Specif i cally speaking, the following four general areas are discussed: (1) ensemble prediction system including initial condition and model/physics perturbations, optimal ensemble size, model resolution, data assimilation, and various "virtual" ensembles; (2) forecast methods including ensemble anomaly forecasting, reforecasting analog ensemble, and storm track clustering; (3) forecast post-processing and calibration including ensemble mean, performance ranking and best member, weighted ensemble mean, probability-matched ensemble mean, and ensemble of dynamic factors; and (4) weather system analysis and model initial condition improvement including perturbation difference analysis, ensemble sensitivity, and targeted observation. It is expected that this review will inspire actions from both operation and research communities: many proven-to-be effective methods described in this paper could be adopted in routine weather forecasting practice by operational meteorologists to improve their forecast and service; research community could have a new starting point with new ideas and a clearer direction for future science and technology development including the improvement of current existing operational ensemble prediction systems in years to come.
heavy rain, ensemble forecasting, forecast calibration, weather diagnosis, targeted observation, data assimilation
10.3969/j.issn.2095-1973.2014.05.001
2013年10月18日;
2014年1月6日
杜钧(1962—),Email: Jundu_noaa@yahoo.com
资助信息:国家自然科学基金(41275107)