Adaptive Robust Waveform Selection for Unknown Target Detection in Clutter

Lu-Lu Wang, Hong-Qiang Wang, Yu-Liang Qin, and Yong-Qiang Cheng

Adaptive Robust Waveform Selection for Unknown Target Detection in Clutter

Lu-Lu Wang, Hong-Qiang Wang, Yu-Liang Qin, and Yong-Qiang Cheng

—A basic assumption of most recently proposed waveform design algorithms is that the target impulse response is a known deterministic function or a stochastic process with a known power spectral density (PSD). However, it is well-known that a target impulse response is neither easily nor accurately obtained; besides it changes sharply with attitude angles. Both of the aforementioned cases complicate the waveform design process. In this paper, an adaptive robust waveform selection method for unknown target detection in clutter is proposed. The target impulse response is considered to be unknown but belongs to a known uncertainty set. An adaptive waveform library is devised by using a signal-to-clutter-plus-noise ratio (SCNR)-based optimal waveform design method. By applying the minimax robust waveform selection method, the optimal robust waveform is selected to ensure the lowest performance bound of the unknown target detection in clutter. Results show that the adaptive waveform library outperforms the predefined linear frequency modulation (LFM) waveform library on the SCNR bound.

Index Terms—Adaptive waveform library, clutter, minimax robust selection, target detection.

1. Introduction

In active sensor systems, the transmitted waveform plays a key role in improving system performance. More importantly, the electromagnetic environment is very complex. Not only may the target of interest have a complex movement, but also the disturbance may be nonstationary. Therefore, to maintain a stable optimal performance, the transmitted waveform should change adaptively with the changing environment.

In an optimal waveform design for target detection, the maximization of signal-to-interference-plus-noise ratio (SINR), which is related to the probability of detection, was usually the criterion described in [1] to [4]. The optimal waveform selection is essentially similar to the waveform design, which selects a waveform from a defined waveform library according to a given criterion[5]-[7]. In the literature on waveform optimization, a basic assumption is that the target impulse response is known or a stochastic process with a known power spectral density (PSD). However, in target detection problems, it is unknown whether a target exists or not. Further, a practical target impulse response is neither easily nor accurately obtained and it changes sharply with the attitude angles, which makes the assumption invalid. In [8], the uncertainty of target aspect was considered and modeled as a normal distribution, so the maximization of the SINR is aspect-averaged. Joint optimization of the transmission waveform and the receiving filters for extended target detection with imprecise prior knowledge of the target impulse response was investigated in [9], where a minimax approach was utilized. Also in [10], a minimax approach was used to design the optimal waveform for multiple-input multiple-output (MIMO) radars under unknown target scattering matrices. It has also been noticed that the precise characterization of the target PSD is rare in practice. Therefore, Yang et al.[11]assumed that the PSD lies in an uncertainty class of spectra limited between the known upper and lower bounds, which markedly relaxes the required priori knowledge of a target, and a minimax robust waveform design method was proposed.

Previous work has been performed to analyze the SINR loss of the optimal waveform when the target impulse response is inaccurate[12]. In this paper, the target impulse response is assumed to be unknown but belongs to a known uncertainty set. In contrast to the existing literature, an adaptive waveform library is designed taking account of the environment. Then the minimax method is utilized to select the robust waveform from the library. The proposed adaptive robust waveform selection method integrates the adaptive signal-to-clutter-plus-noise ratio (SCNR)-basedwaveform design algorithm and the minimax robust signal processing technique. This paper proposes an adaptive waveform library design method that has several advantages, for example, the waveform library is adaptively designed according to the environment and if the optimal waveform of the target impulse response is the selected robust waveform, the selected waveform is the optimal one for the specific target.

2. SCNR-Based Waveform Design

In this section, the SCNR-based waveform design method for target detection with a known target impulse response is introduced. We adopt the most widely used signal model (shown in Fig. 1) and make a brief review of this procedure[4]. Letbe a known complex-valued baseband target impulse response of finite durationhT and its Fourier transform bebe the complex-valued receiver filter impulse response andbe a complex-valued, zero-mean channel noise process with PSDwhich is non-zero over the entire waveform bandwidth. A complex-valued, zero-mean Gaussian random process denoted by ()c t represents the clutter and is characterized by the PSD. The complex-valued baseband transmit waveform iswith finite-energy, duration T, and the Fourier transform

The SCNR at the output of the receive filter at time0t can achieve its maximum value[4]:

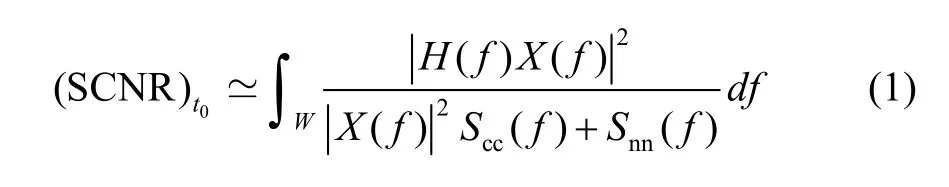
if and only if the matched filter is of the form

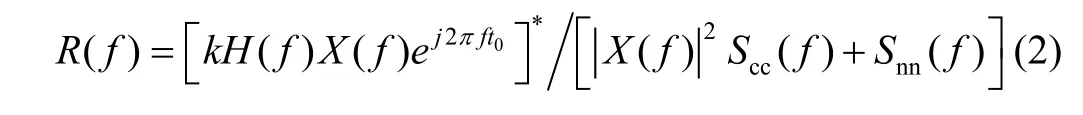
where k is an arbitrary constant, and ∗ denotes complex conjugate. The transmitted signal is assumed to be essentially limited to the bandwidth W, and the waveform energy constraints can be written as

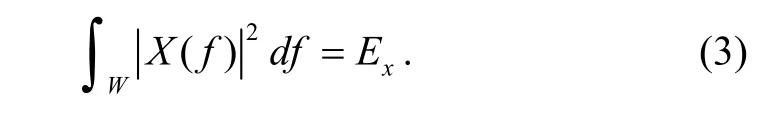
By using the Lagrangian multiplier technique, the optimal waveform which maximizes SCNR under the energy constraint is

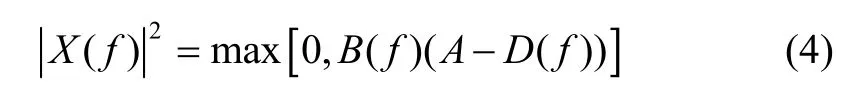
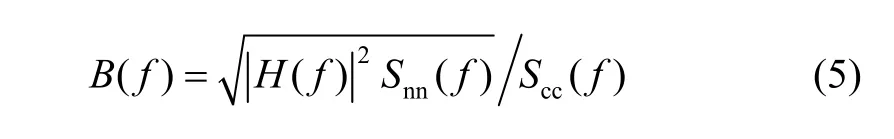
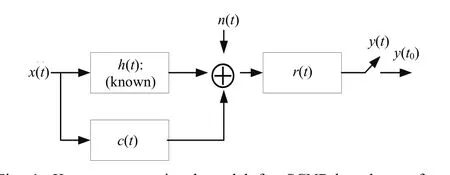
Fig. 1. Known target signal model for SCNR-based waveform design.

and

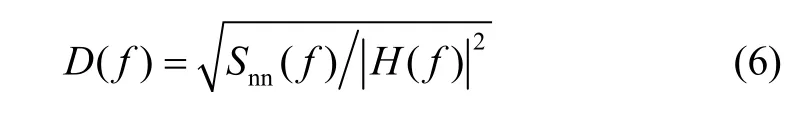
respectively, and A is a constant determined by the energy constraint

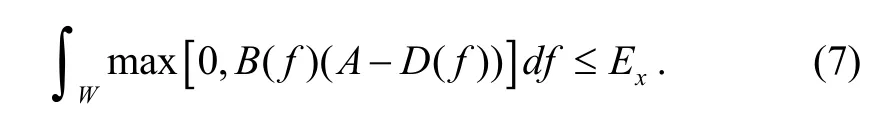
For a given Ex, once A is calculated according to (7), the optimal waveform as well as the maximized SCNR is found by substituting (5) and (6) into (4). This is called water filling in most of the waveform design methods, which is a terminology first used in the information theory[13].

If the prior knowledge of the target impulse response is known, we can easily design the optimal transmit-receiver pair to obtain the maximum SCNR. In this case, the best detection performance of the specific target will be obtained. However, in practice we never know whether the target exists or not, not to mention the target impulse response. Therefore, the above maximum SCNR in (4) is seldom obtained, and the optimal waveform for unknown target detection should be investigated.

3. Unknown Target Detection in Clutter

Suppose that the target impulse response is unknown, but we have the prior knowledge that the target impulse response belongs to a known setwhich contains N types of target impulse responses. This assumption is reasonable as we can limit the overall targets we are going to detect, for example, certain types of trucks, tanks, and ships. Or we can regard the N target impulse responses as the target impulse response for a certain target with N different attitude angles. We are going to detect whether the specific target exist or not but have no idea of its attitude angle. Therefore, the target impulse response is unknown but is one of the elements in the set T. The clutter is modeled as a complex-valued, zero-mean Gaussian random process, with a given PSDwhere λ is a parameter used to model the changing environment. Channel noise is modeled as a complex-valued, zero-mean Gaussian random process with a flat PSDThe transmitted signal isselected from a waveform librarywhere M is the total number of transmitted waveform types. The design of the waveform library is an important problem. The optimal waveform is selected from Ψ to detect the target where the target impulse response is unknown but pertains to the known set T.

The signal model is similar to that in Fig. 1, except that the target impulse response isis the transmitted waveform in set Ψ. ()c t denotes the clutter with PSDis known but will change to represent the changing environment. Then SCNR can be represented by

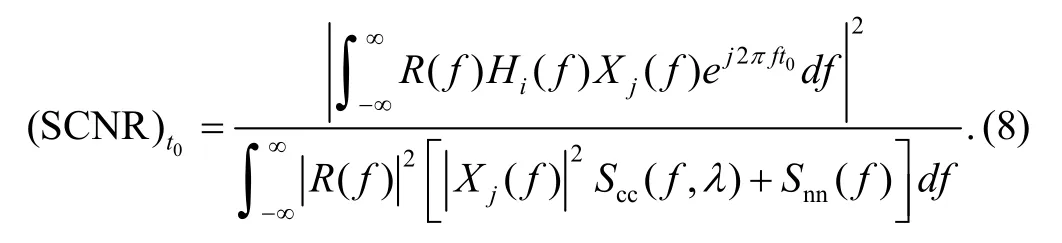
As the prior knowledge of the target impulse response is unknown, the receiver filter is of the form:

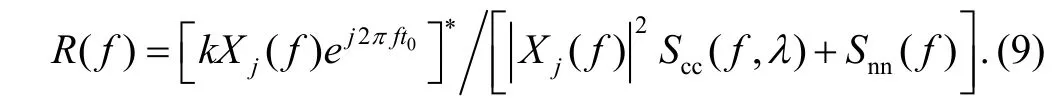
Applying the same assumption that the transmitted signal is essentially limited to the bandwidth W, the SCNR is

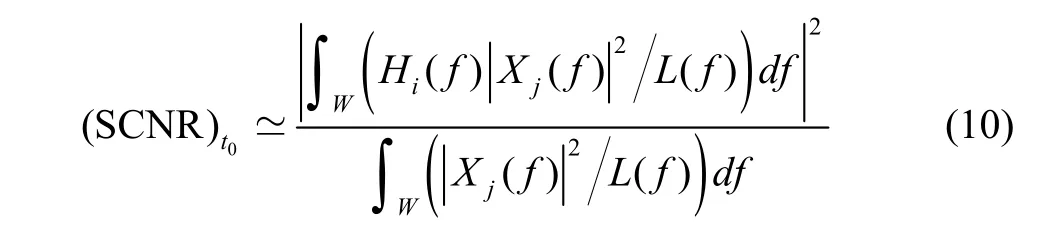
where

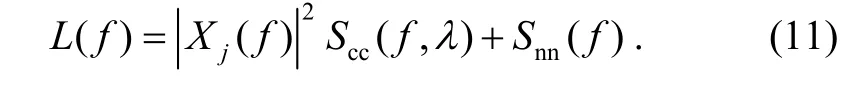
The SCNR expressed in (10) is used to calculate the actual SCNR at the output of the receiver. For an unknown target detection waveform selection, SCNR is also used as the criterion, but should be modified.

4. Adaptive Robust Waveform Selection

It is explicit that the SCNR in (10) is a function of the selected waveform spectrum Xj(f) and target frequency response Hi(f ). As the target frequency response is unknown, we use the minimax robust waveform design method to optimize the worst-case performance, which is a well accepted engineering approach[11],[14]. The optimal waveform should satisfy

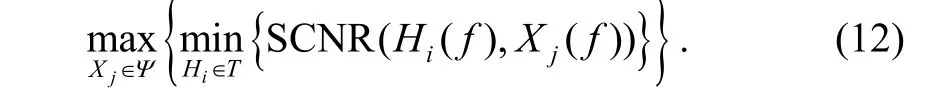
To solve this optimization problem, according to the minimax robust signal processing theory in [15], we need to findthat satisfies

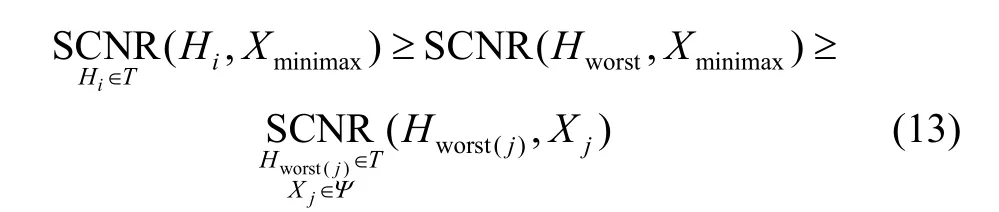
Next, we investigate the problem of how to devise the waveform library. In this paper, the waveform library is adaptively designed, which is dependent on the target set and the environment, including the clutter PSD and noise PSD. An easy and effective way of waveform library design is the ensemble of all the optimal waveform for the target impulse responses in set T under the condition that the target impulse response is known. Therefore, the adaptive waveform library contains N types of waveformswhereis the optimal waveform for the target impulse responseis designed according to (4) under the energy constraint in (3). Obviously, once the target impulse response set T is known, the waveform library is adaptively designed which depends on the environment. This adaptive waveform library along with the minimax selection method has the following advantages: firstly, the lowest performance bound is guaranteed owing to the minimax selection; secondly, if the target present is just the best target impulse response (i.e., Xjis the robust waveform while Hjis the target frequency response), the output SCNR is the largest of all waveforms. Therefore, by guaranteeing the lowest bound and maximizing the largest value, the adaptive waveform library is expected to have good performance.

5. Simulation Results

By using the proposed adaptive robust waveform selection method, we can adaptively design the waveform library and select the minimax robust waveform. Suppose that the uncertainty target impulse response set T contains four types of target impulse responses, i.e.,. Clutter PSD is assumed to be Gaussian with fixed standard derivation, but the mean value can be changed to illustrate the changing environment. The noise is additive white Gaussian noise (AWGN). The target-to-noise ratio (TNR) is defined as the target energy to the area under the noise PSD curve. The clutter-to-noise ratio (CNR) is strictly the area ratio under the PSDs curve. The TNR and CNR are set to 0 dB. Fig. 2 depicts the frequency responses of the four types of targets, the clutter PSD with the mean of 30 Hz, and the noise PSD. The adaptive waveform library is shown in Fig. 3 (a), in whichis the amplitude response of the optimal waveform for the targetunder the energy constraint ofby using the SCNR-based waveform design method. All the waveforms in the adaptive waveform library have the characteristic that they allocate small energy into the frequency band where the clutter power is strong, meanwhile, they concentrate their energy into the frequency band where the target energy is strong.

For comparison, another fixed waveform library of linear frequency modulation (LFM)signals (shown in Fig. 3 (b)) is designed. We denote these waveforms asThey are predesigned and fixed, with the same energy ofWe apply the minimax robust waveform selection method for the two waveform libraries and compare their performance.

Applying the minimax robust waveform selection methods described in Section 4 to the adaptive waveform library when the mean value of the clutter PSD is assumed to be 30 Hz, we obtain the result that the least favourable target frequency response isthe minimax robust optimal waveform selection isand the SCNR bound is 13.36 dB. This means that if we use the robust waveformto detect targets, no matter which target appears, the SCNR obtained is at least 13.36 dB, which is the performance bound of the detection problem. The results are shown in Fig. 4. The least favourable target frequency response has a similar frequency band to that of the clutter PSD. Therefore, the SCNR using the waveformreaches its lowest value if the targetis present, becausehas a spectral notch at the frequency band of the clutter PSD, which affects the energy of the target echo. However, it is the largest bound compared with those by using other waveforms.

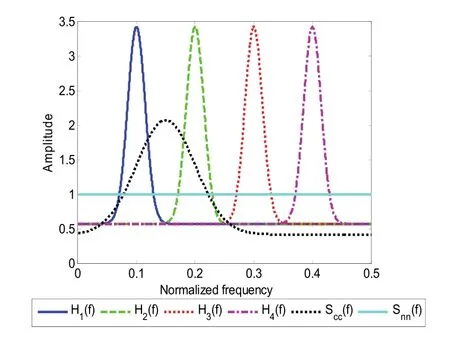
Fig. 2. Target frequency responses, clutter PSD, and noise PSD.

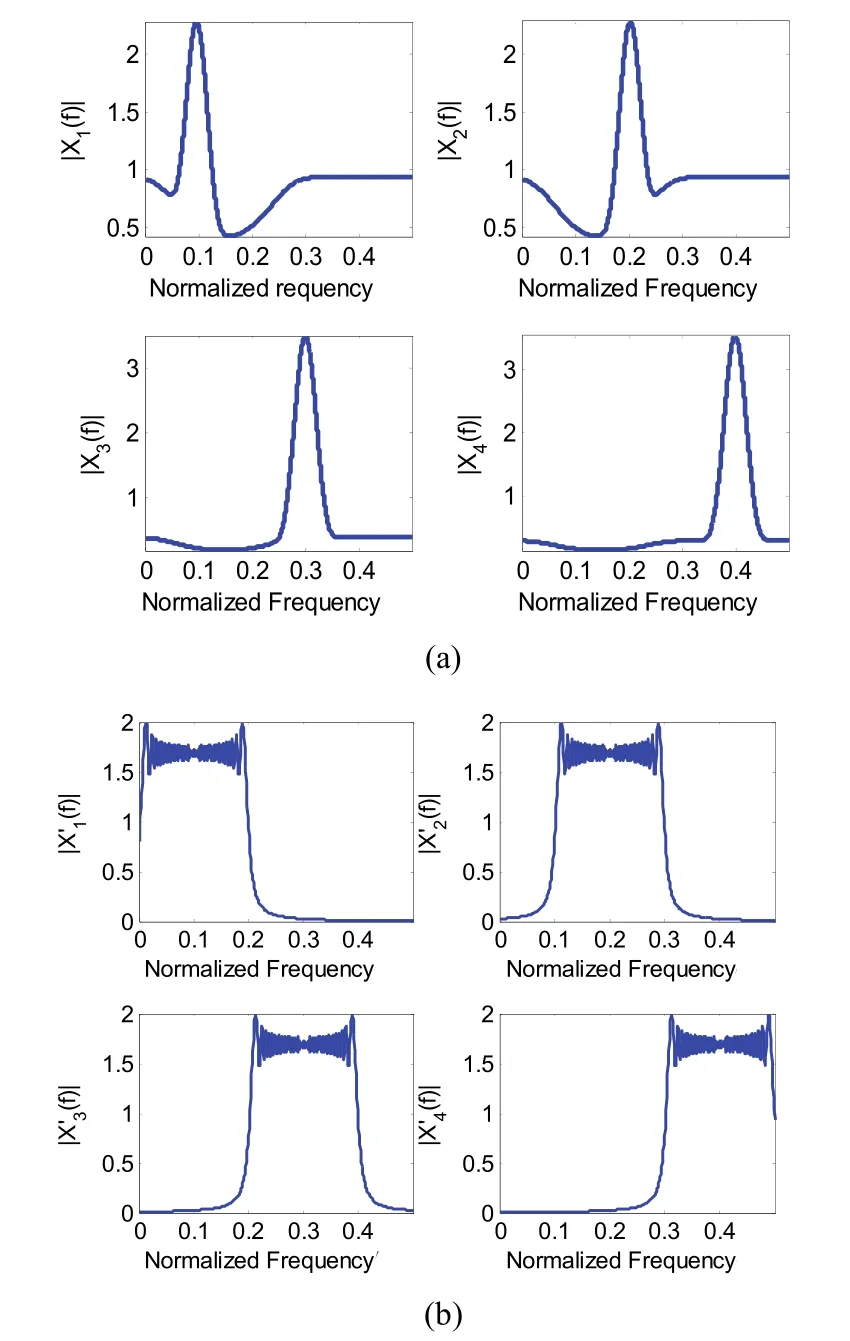
Fig. 3. Two waveform libraries: (a) adaptive waveform library and (b) predefined LFM waveform library.

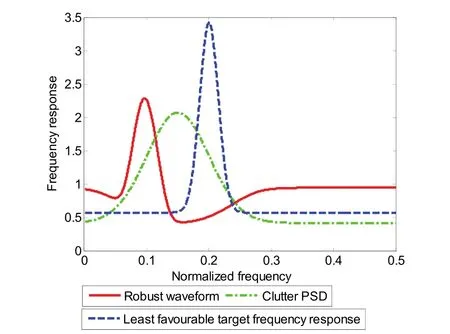
Fig. 4. Simulation results for the adaptive waveform library.

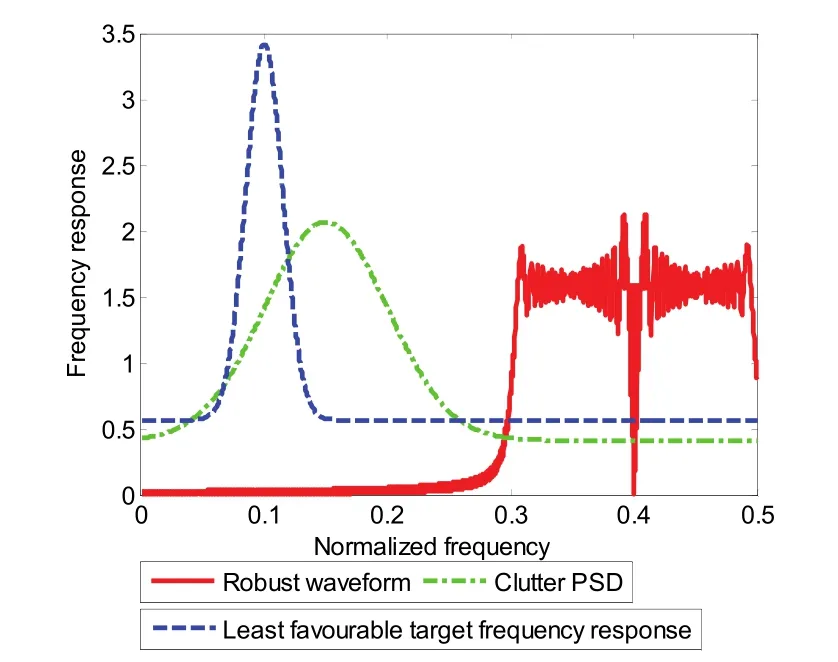
Fig. 5. Simulation results for the predefined LFM waveform library.

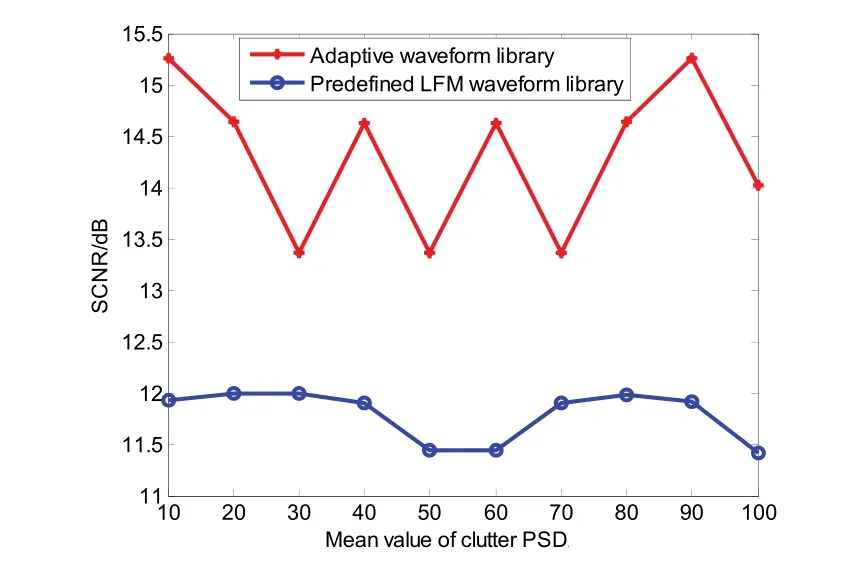
Fig. 6. SCNR bound with changing environment.

For the predefined waveform library in Fig. 3 (b), we also apply the minimax robust waveform selection method. As shown in Fig. 5, the least favourable target frequency response is1()H f, the minimax robust optimal waveform selection is4()X f′ , and the minimax SCNR bound is 11.99 dB. Among all the four waveforms in the predefined LFM waveform library,4()X f′ is the optimal robust waveform, which guarantees the minimum value of SCNR to be no smaller than the SCNR bound no matter which target exists, and this SCNR bound is the largest one compared with those using the other three waveforms. The smallest SCNR value occurs when the least favourable target frequency responseis present. It is manifested thatandshare the similar frequency band, which leads to a low SCNR.

Fig. 6 shows the SCNR bound obtained by using the minimax robust waveform selection method for the adaptive waveform library and the predefined LFM waveform library when the mean value of clutter PSD is changing from 10 Hz to 100 Hz, with a step of 10 Hz. It is evident that the SCNR bound for adaptive robust waveform selection is improved. When the environment (the mean value of clutter PSD) is changing, the SCNR obtained by applying the minimax robust waveform selection method for the adaptively designed waveform library is always larger than the SCNR obtained by the same method for the predefined LFM waveform library. Notice that this adaptive waveform library is designed on-line with the information of the real-time environment, thus it will be more time consuming than the predefined LFM waveform library. However, the calculation method for each waveform in the adaptive waveform library is the same; therefore, parallel methods can be utilized to obtain each waveform simultaneously.

6. Conclusions

In this paper, the target impulse response is assumed to be unknown but belongs to a known uncertainty set, which relaxes the required prior knowledge. An adaptive waveform library is designed by using the SCNR-based waveform design method. Then the minimax robust selection method is used to guarantee the worst-case performance. This ensures that, if the optimal waveform of the target impulse response is the selected robust waveform, then the selected waveform is the optimal one for the specific target. Therefore, the best performance for the existing target detection is obtained. Simulation results show that this adaptive robust waveform selection method is easy to realize and has a superior performance bound than merely selecting a robust waveform from a predefined LFM waveform library. This method can be utilized to improve the target detection performance in the absence of information on the target impulse response. However, this paper only proposes one method of adaptive waveform library design. Future work will be on the investigation of waveform library design methods with the potential to substantially affect the performance bound.

[1] M. R. Bell, “Information theory and radar waveform design,”IEEE Trans. on Information Theory, vol. 39, no. 5, pp. 1578-1597, 1993.

[2] M. R. Bell, “Information theory and radar: Mutual information and the design and analysis of radar waveforms and systems,” Ph.D. dissertation, California Institute of Technology, Pasadena, 1988.

[3] S. U. Pillai, H. S. Oh, D. C. Youla, and J. R. Guerci,“Optimum transmit-receiver design in the presence of signal-dependent interference and channel noise,” IEEE Trans. on Information Theory, vol. 46, no. 2, pp. 577-584, 2000.

[4] R. A. Romero, J. Bae, and N. A. Goodman, “Theory and application of SNR and mutual information matched illumination waveforms,” IEEE Trans. on Aerospace and Electronic Systems, vol. 47, no. 2, pp. 912-927, 2011.

[5] H. Wang, H. Xia, Y. Cheng, and L. Wang, “Adaptive waveform selection for target tracking based on MPDA,”Systems Engineering and Electronics, vol. 33, no. 11, pp. 2389-2392, 2011(in Chinese).

[6] B. F. La Scala, W. L. Moran, and R. J. Evans, “Optimal adaptive waveform selection for target detection,” in Proc. of the Int. Radar Conf., Adelaide, 2003, pp. 492-496.

[7] D. J. Kershaw and R. J. Evans, “Optimal waveform selection for tracking systems,” IEEE Trans. on Information Theory, vol. 40, no. 5, pp. 1536-1550, 1994.

[8] D. A. Garren, M. K. Osborn, A. C. Odom, J. S. Goldstein, S. U. Pillai, and J. R. Guerci, “Optimal transmission pulse shape for detection and identification with uncertain target aspect,”in Proc. of the 2001 Radar Conf., Atlanta, 2001, pp. 123-128.

[9] B. Jiu, H. Liu, D. Feng, and Z, Liu, “Minimax robust transmission waveform and receiving filter design for extended target detection with imprecise prior knowledge,”Signal Processing, vol. 92, no. 1, pp. 210-218, 2012.

[10] E. Grossi, M. Lops, and L. Venturino, “Min-max waveform design for MIMO radars under unknown correlation of the target scattering,” Signal Processing, vol. 92, no. 6, pp. 1550-1558, 2012.

[11] Y. Yang and R. S. Blum, “Minimax robust MIMO radar waveform design,” IEEE Journal of Selected Topics in Signal Processing, vol. 1, no. 1, pp. 147-155, 2007.

[12] L. Wang, H. Wang, Y. Qin, and Y. Cheng, “Analysis of SINR loss for waveform design of known-target in signal-dependent interference,” in Proc. of 2012 Int. Waveform Diversity and Design Conf., Hawaii, 2012, pp. 260-265.

[13] T. M. Cover, and J. A. Thomas, Elements of Information Theory, 2nd ed. New York: Wiley, 2006.

[14] E. Grossi, M. Lops, and L. Venturino, “Robust waveform design for MIMO radars,” IEEE Trans. on Signal Processing, vol. 59, no. 7, pp. 3262-3271, 2011.

[15] S. A. Kassam, and H. V. Poor, “Robust techniques for signal processing: A survey,” Proc. of the IEEE, vol. 73, no. 3, pp. 433-481, 1985.

Lu-Lu Wangwas born in Henan, China in 1988. She received the B.S. degree in electrical engineering from National University of Defense Technology (NUDT), Changsha in 2009. She is currently pursuing her Ph.D. degree with the School of Electronic Science and Engineering, NUDT. Her research interests include statistical signal processing and adaptive radar waveform design.

Hong-Qiang Wangwas born in Shanxi, China in 1970. He received his Ph.D. degree from NUDT in 2002. He is currently a professor with the School of Electronic Science and Engineering, NUDT. His research interests are automatic target recognition, radar imaging, and target tracking.

Yu-Liang Qinwas born in Shandong, China in 1980. He received his Ph.D. degree from NUDT in 2008. He is currently an associate professor with the School of Electronic Science and Engineering, NUDT. His research interests include signal processing in precise guidance.

Yong-Qiang Chengwas born in Hebei, China in 1982. He received his M.S. and Ph.D. degrees from NUDT in 2007 and 2012, respectively. He is a lecturer with the School of Electronic Science and Engineering, NUDT. His research interests include information geometry and statistical signal processing.

Manuscript received February 21, 2013; revised April 16, 2013. This work was supported by the National Natural Science Foundation of China under Grant No. 61171133, the Natural Science Fund for Distinguished Young Scholars of Hunan Province under Grant No. 11JJ1010, and the Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20124307110013.

L.-L. Wang is with the School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China (Corresponding author e-mail: lulu.wang@ucl.ac.uk).

H.-Q. Wang, Y.-L. Qin, and Y.-Q. Cheng are with the School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China (e-mail: oliverwhq@tom.com; yuliangqin@gmail.com; nudtyqcheng@gmail.com).

Color versions of one or more of the figures in this paper are available online at http://www.intl-jest.com.

Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.02.018