具有时滞和HollingⅢ型功能反应的三种群捕食模型的全局渐近稳定性

官金兰，房少梅

具有时滞和HollingⅢ型功能反应的三种群捕食模型的全局渐近稳定性

官金兰1，房少梅2

（1.广东农工商职业技术学院基础部，广东广州510507；2.华南农业大学理学院，广东广州510642）

研究具有时滞和HollingⅢ型功能反应的一个捕食者两个食饵的三种群捕食系统，通过构造Lyapunov函数，给出该系统全局渐近稳定的充要条件，最后用Matlab软件对所得的理论结果进行数值仿真．

时滞；HollingⅢ型功能反应；Lyapunov函数；全局渐近稳定；数值仿真

捕食者—食饵系统是生态学中描述种群动力学的一类非常重要的模型，而带有功能性反应函数的系统能更确切地描述实际的生态捕食情况，这方面已有一些很好的研究工作［1-5］.如文献［1］研究了HollingⅡ型功能反应函数对一个捕食者两个食饵的捕食系统的影响.由于HollingⅡ型功能反应函数是线性的，它只能描述类似藻类细胞动物和无脊椎动物这样的简单捕食系统，还要对系统的很多因素进行忽略，才能用线性函数来进行描述.为了能准确的描述实际生态捕食系统，文献［4］引入HollingⅢ型功能反应函数：ø(x)=ax2/ (a2+b2)，这是一个二次函数，它比HollingⅡ型功能反应函数能更好地描述实际的生态捕食系统，描述的捕食系统范围也比较大，包括了脊椎动物在内的捕食系统.

在一个捕食者两个食饵的捕食系统中，由于两个食饵躲避捕食者的捕捉能力不一样，所以每个食饵对捕食者的HollingⅢ型功能反应函数是不同的，与此同时，在生态系统中，时滞能更好地描述实际情况.

因此本文在一个捕食者两个食饵的3种群Volterra型捕食模型［1］:

的研究基础上，建立如下具有时滞和HollingⅢ型功能反应的一个捕食者两个食饵的3种群捕食模型:其中xi(t)(i=1,2)分别表示两食饵的种群密度，x3(t)表示捕食者种群的密度．τ1,τ2分别表示两食饵种群x1(t),x2(t)负反馈引起的时滞，τ3为捕食者种群从幼年到成年的成熟期，而且捕食者种群只有到了成年后才具有捕食能力．ri,aij(i,j=1,2,3),α,β都为正常数，τ=max{τ1,τ2,τ3}．xi(t)(i=1,2,3)都是定义在区间［-τ,+∞)上的连续可微函数．本文主要研究系统（1）的正平衡点的全局稳定性．通过构造Lyapunov函数，证明得到该系统全局渐近稳定的充要条件，最后用Matlab软件对所得的理论结果进行数值仿真．

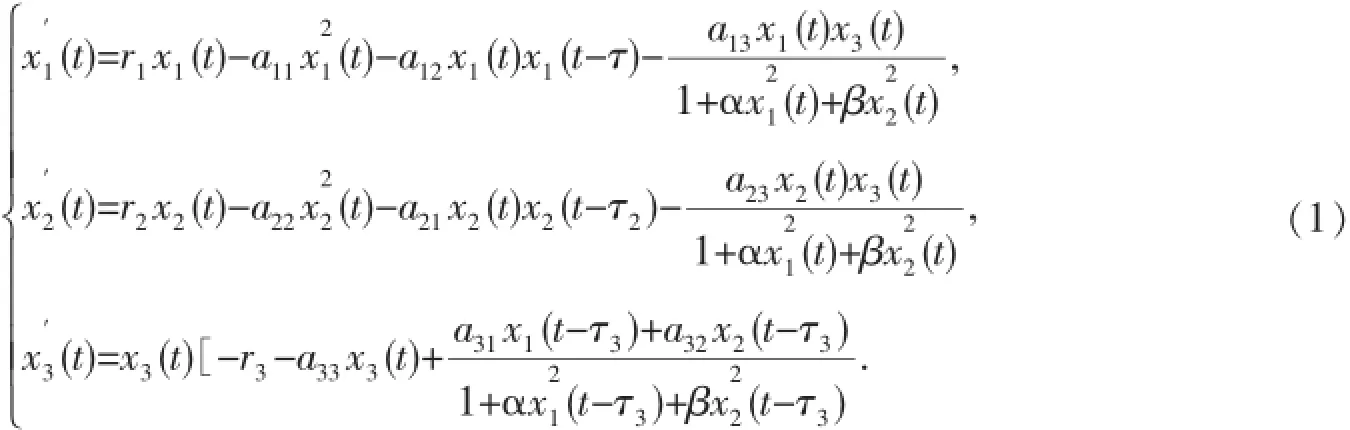
1 预备知识

假设系统（1）满足下列条件：

则存在T>0,对所有τ>T有：

其中，

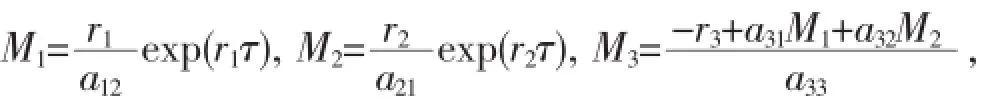
由于系统（1）的3个种群的密度xi(t)(i=1,2,3)相互之间具有循环的相同类型的影响，因此本文约定集合⊂R+×R+×R+，其中={x∈R3|xi≥0,i=1,2,3}．

定义1函数V(N)称为是连续时间生态模型：

（1）V(N*)=0,V(N)>0，当N≠N*时，其中N*为生态模型（2）的正平衡点；

（2）V(N)=k，对每一个正值K是一个闭的超曲面，且V(N)→∞，当N→0或VN→∞时［6］.

定义2对连续生态模型（2），如果存在上述定义的正定且无限大的V函数，使得V(N(t))<0，则称生态模型（2）的正平衡点N=N*是全局稳定的［6］．

2 主要结果

引理1（解的存在性）系统（1）至少存在唯一满足以下初始条件：

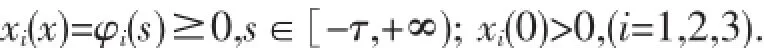
的解，这里φi(s)(i=1,2,3)均在区间［-τ,+∞)上连续可微．证系统(1)可以写成如下的一个初值问题：

其中

则其对应的雅可比矩阵：

引理2如果系统（1）的初值恒大于零，则系统（1）的解一定为正解.

证设x(t)=(x1(t),x2(t),x3(t))是系统（1）的任意一组解，代入系统（1），由假设(H1),(H2),(H3)，m1,m2,m3,M1,M2, M3均大于零，且有：

然后在［0,t］上积分，有：

当t=0时，C1=C2=x1(0),C3=C4=x2(0),C5=C6=x3(0)，所以x1(t),x2(t),x3(t)均大于零．所以引理2成立．

定理1系统（1）存在正平衡点x*=(x1*(t),x2*(t),x3*(t))，且x*全局渐近稳定的充要条件是(H1),(H2),(H3)条件成立，且满足：

证设x(t)=(x1(t),x2(t),x3(t))是系统（1）的任意一组正解，根据(H1),(H2),(H3)和引理1，存在正的常数mi(i=1,2,3)，使对所有的t≥T，有：

构造Lyapunov函数［6］如下：

则V(t)沿着系统（1）的任意正解的右导数为：

令：

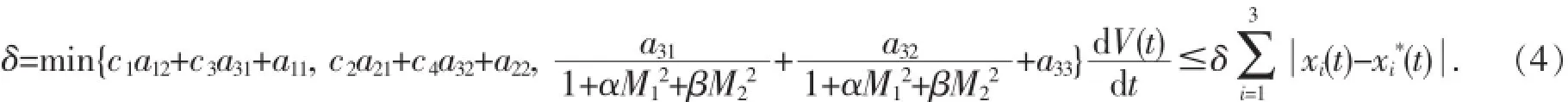
对（4）在［T,t］上积分，则有：(i=1,2,3)及其导数在［T,+∞］上有界，

所以系统（1）的任意正解是稳定的且是全局渐近稳定的．

3 数值仿真

利用Matlab求解微分方程（1）的数值解，设置方程的系数为：r1=2,a11=1,a12=2,a13=0.5,r2=2,a21=1,a22= 0.2,a23=0.1,r3=1,a31=0.5,a32=0.5,a33=0.2,α=0.5,β=0.5编写Matlab程序运行，可以得到如图1所示的密度分布图及相图．

从图1中可以看出，经过一定的时间后，3个种群都达到平衡，x1(t),x2(t),x3(t)分别在x1(t)=0.812 2,x2(t)= 0.083 5,x3(t)=0.465 7处达到平衡．

图1 三种群的密度分布图和相图

4 结论

生态种群之间在满足一定的条件下，它们相互依存的数量变化最终都将趋于稳定，达到现实生活中的生态平衡．但影响种群达到平衡的因素很多，既有自然的因素，如环境的容纳量和资源的数量有限等；也有人为的因素，如人类对环境的破坏会对种群的平衡产生很大的影响．所以，接下来的工作，就是要对系统（1）进行改进，把环境和人为的因素加以考虑，使之更符合实际的生态系统．

［1］程惠东,藏秀红,张伟伟.具有HollingII类型功能反应的3种群捕食时滞模型［J］.数学的实践与认识，2008，38(13)：130-133.

［2］王稳地.带时滞的生态模型的渐近性态［J］.生物数学学报,1997，11(5):1-7.

［3］徐瑞,陈兰荪.具有时滞和基于比率的三种群捕食系统的持久性与全局渐近稳定性［J］.系统科学与数学,2001，21(4):204-212.

［4］陈兰荪．数学生态学模型与研究方法［M］．北京：科学出版社出版,1988.

［5］Wangersky P J,Cuningham W J.On time lage in equations of growth［J］.Proc Acad Sci USA,1956,4(2):6992-7002.

［6］陈菊芳,杨霞．生态系统中Lyapunov函数的构造［J］．生物数学学报，1996，11(3)：12-23.

［7］钟益林，彭乐群，刘炳文．常微分方程及其Maple,MATLAB求解［J］．北京：清华大学出版社，2007．

On the three population predator-prey model with time delay and HollingⅢ-type functional response

GUAN Jin-lan1,FANG Shao-mei2
(1.Department of Basic Courses，Guangdong Agricultural Industry Business College，Guangzhou 510507，Guangdong,China；2.College ofScience,South China AgriculturalUniversity,Guangzhou 510642,Guangdong,China)

This paper studies the three population Predator-prey model with time delay and HollingⅢ-type functional response.By constructing Lyapunov function,it provides the sufficient condition for global asymptotic stability,and ituses Matlab software to simulate the theory result.

HollingⅢ-type functional response;time delay;Lyapunov function;global asymptotic stability; numerical simulation

O175.2

A

1007-5348（2014）04-0005-05

（责任编辑：邵晓军）

2013-12-22

国家自然科学基金项目（11271141）.

官金兰（1982-），女，广东韶关人，广东农工商职业技术学院基础部讲师，博士，主要从事生物数学模型与可视化方面的研究.