Prediction-based Manufacturing Center Self-adaptive Demand Side Energy Optimization in Cyber Physical Systems
2014-03-01SUNXinyaoWANGXueWUJiangweiandLIUYouda
SUN Xinyao, WANG Xue, WU Jiangwei, and LIU Youda
State Key Laboratory of Precision Measurement Technology and Instrument, Tsinghua University,Beijing 100084, China
1 Introduction
CPS(cyber physical systems) has recently emerged as a technology which has the potential to bring great changes to the power industry throughout the world. Combining cyber technologies capable of sensing, communicating,computing and controlling with physical energy systems,CPS could make future industrial power systems more flexible, efficient, sustainable, reliable and secure. The achievement of these capabilities will require the installation of smart meters, intelligent sensors and actuators, double sided energy user and provider communication and control networks as well as adaptive system models and data processing methods to deal with the big data generated by industrial systems[1].
Cyber physical systems have four fundamental characteristics. First, CPS uses extensively deployed distributed sensor networks to perform the ubiquitous sensing and collecting of real time information to monitor the complex physical systems dynamics. Second, the computing and analysis of the collected data is carried out on the embedded computing devices and important knowledge extracted through data mining and processing in real time. Third, CPS depends heavily on double sided communication networks to transmit data between sensors,computational devices, and actuators. Finally, the CPS can be manipulated and controlled to meet predetermined requirements by integrating the sensing, computing and communication technologies.
This paper interprets CPS as a future type of industrial power system and recognizes the manufacturing center as a subsystem of the CPS. The main focus of this paper is to propose a more optimal method for controlling the CPS while scheduling the operation of the manufacturing center.
CPS now has the capability, by using real time sensing and automatic controlling, to solve the problem of energy optimization of demand side electric networks. This capability is referred to as demand side management(DSM)[2]. DSM is a hot research spot in industrial power systems. It has significant implications for environmental issues, transmission and distribution deficiencies, and peak load problems. In the general energy optimization process,the DSM system collects and processes information from the demand side industrial power systems(such as the manufacturing center) and informs the central controller about optimized load profiles and available shifting or load reducing possibilities for each of the next day time slots[3].The goal of DSM is to obtain the best trade-off between demand side service quality and energy consumption or peak load demand. Compared with traditional power systems, CPS has the capability to measure and control larger numbers of variables in real time. Consequently, CPS can enhance the efficiency of demand side energy optimization.
The system dynamics or real time status of electric devices in the CPS can be measured by the advanced metering infrastructure(AMI) sensing system. The sensing layer of the AMI deploys a tremendous number of smart sensors and smart meters to capture and process in a distributed and collaborative manner the information needed for load control and energy management. The AMI has a two way communication capability which can transmit data using such advanced communication technologies as power-line carrier communications and wireless communication networks. The AMI, furthermore,provides the basic information and platform for implementing demand side energy optimization in CPS.
There has been a great increase recently in research into energy-saving strategies and energy optimization methods in industrial power systems. Sun proposed an instantaneous power-balancing optimization energy management method to enhance the economic performance of a novel parallel series hybrid electric bus[4]. Tong developed an information fusion based numerical control machining progress monitoring scheme which could obtain in real time the production status of work in process[5]. He proposed a systematic methodology that incorporates energy consumption and environmental impact considerations into the production operations and provide opportunities for reducing energy consumption in the machining process[6].Xu designed an energy regulation based variable-speed electrohydraulic drive system and a three-layer back propagation neural network to deduce the energy state[7].
Researchers in recent years have proposed the use of several demand side management methods. Most of the techniques remain in the system strategies level. They are not suitable for real world power systems that have complicated dynamics and large numbers of distributed devices[3]. Many DSM methods have been proposed which utilize linear/dynamic programming[8–9]. These methods are not adequate, however, for systems composed of different physical components types which require differing computation patterns. Direct load control(DLC) is a common method used to control load management for specific types of electrical utilities, such as air conditioning systems to improve the reliability and operating costs of demand side industrial power systems[10]. Intelligent computing (e.g., fuzzy systems) have proven to be a reliable way for DLC to optimize customer satisfaction and energy savings as long as some experience parameters and rules are appropriately selected[11]. In the future, customers will demand discrete industrial power systems for specific functions. They will have different requirements for decentralized and diversified control over their energy consumption. Traditional centralized DLC programs which provide uniform control systems will be incapable of meeting this challenge.
The particle swarm optimization method(PSO) uses an intelligent iterative algorithm to optimize the solution to a problem by testing and improving each candidate solution sequentially in a manner that can be likened to the behavior of a flock of birds[12]. PSO has been adopted to solve a wide range of optimization problems. Recently, several attempts have been made to enhance PSO performance[13]. The co-evolutionary particle swarm optimization method(CPSO), inspired by the results it has been able to achieve in analyzing co-evolving populations, has demonstrated the potential to improve PSO algorithm results. In CPSO,multiple swarms are introduced to optimize solution vectors[14]. Compared with PSO, CPSO has performed better in solution quality and robustness, but it may still be trapped in suboptimal solution iterations.
In power systems, real time demand needs to be matched to power availability (i.e., the energy user’s needs have to be anticipated in advance). Therefore, load forecasting,particularly short-term demand side load forecasting(STLF),is a capability which is required to resolve the DSM issue.Various methods—including the regression model, time series approaches, neural networks, expert systems and support vector machines—have been proposed[15–19]. The performance of these methods, however, might have been constrained by such factors as the nonlinear relevance between load and exogenous factors, the subjective influence of the model’s designers, insufficient input training data, the over-fitting of the problem caused by irrelevant training data, etc. The sparse Bayesian learning(SBL) is a novel probability and kernel based algorithm which can obtain accurate predictions while using significantly fewer basis functions than SVM and at the same time present various advantages[20]. The SBL prediction framework provides an encouraging approach for predicting probabilistic distributions of nonlinear and non-stationary processes.
This paper presents a prediction-based manufacturing center self-adaptive energy optimization method for demand side management in CPS. The presentation of the proposed new method is organized as follows. Section 2 introduces a componential weighted short-term load forecasting method for predicting electric load levels on a 24-hour basis for a specific industrial location in China. To improve prediction accuracy, an empirical mode decomposition approach is introduced to conduct a componential analysis of the electric load. Section 3 presents a dynamic pricing strategy based on the short-term load forecasting results and optimization problem formulation. Then, in section 4, a CPSO demand side energy optimization algorithm is presented as a CPS subsystem to minimize total energy costs and to guarantee manufacturing center service quality. Section 5 presents the real world load prediction and energy optimization experiment results. Section 6 presents the conclusions.
2 Componential Weighted STLF for CPS
The CPS’s short-term load forecasting(STLF) system can provide such prior knowledge as the next 24-hour load profile and the anticipated peak load required for demand side management. The DSM system can implement the necessary actions based on the load prediction results. The electric load possesses a complex of features at different frequencies. The application of componential analysis of the electrical load has been proven useful and could improve the prediction accuracy of STLF[18]. In this section,we apply a componential probabilistic short-term load forecasting method.
2.1 Componential analysis of electrical load
Empirical mode decomposition(EMD) is a data-driven signal analysis tool which can be adapted for use in non-stationary systems and nonlinear processes. EMD has been implemented to generate the load curve’s intrinsic mode functions(IMFs), and each IMF contains a different frequency component of the load signal. The steps in EMD can be described as follows[21]:
(1) Discern the local maximum and minimum values of input signal s (t).
(2) Perform the cubic spline interpolation to obtain the envelopes eM(t) and em(t) , respectively.
(5) If the local extrema number of c1(t) equals to or differs from the number of zero crossings by one, AND the average of c1(t) is reasonably zero, then c1(t) is an IMF,and if not, repeat the formal steps on c1(t) .
(6) Calculate the residual error,
2.2 Probabilistic load forecasting
We implement Sparse Bayesian learning(SBL) to give a probabilistic load forecasting result. In a general regression problem, the target value tncan be expressed by the input vector xnand an additive noisen:
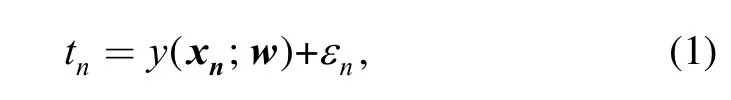
According to the kernel-based prediction method,
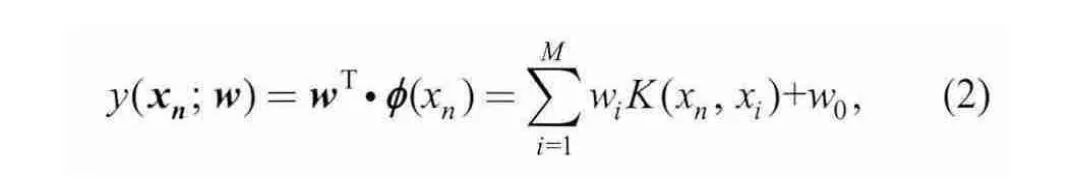
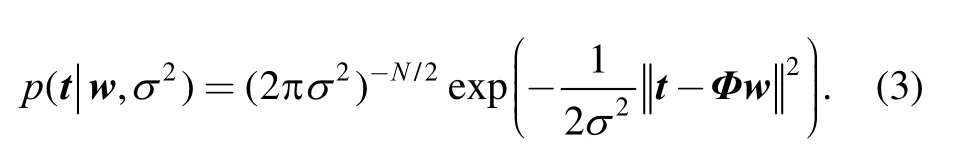
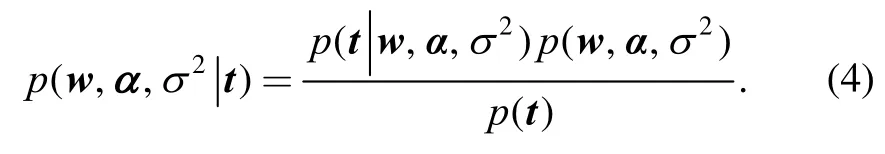
To reduce computation complexity, the posterior distribution of α and2is approximated by Dirac distributionwithMPandthe maximum likelihood estimations forand2, respectively. With the estimated model parameters and a newly produced input datum *x, the distribution of the target*t is calculated by
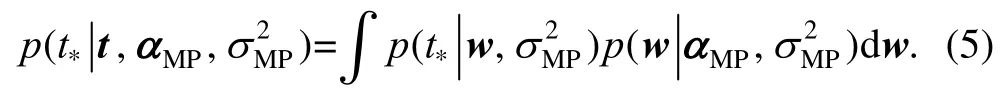
The calculation result shows that y*belongs to a normal distribution, with
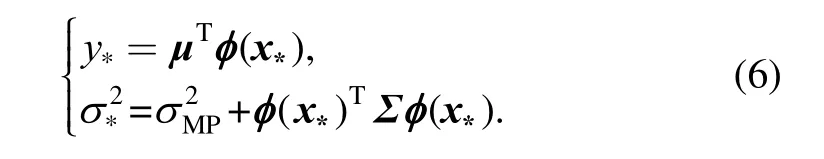
In order to explore the correlation between the training data and to prune the irrelevant input vectors to reduce the training complexity and obtain an optimal forecasting model, we use a Mahalanobis distance based weighting scheme to select a more related input dataset for load forecasting. At this point, we introduce the Gaussian kernel function which can be defined as
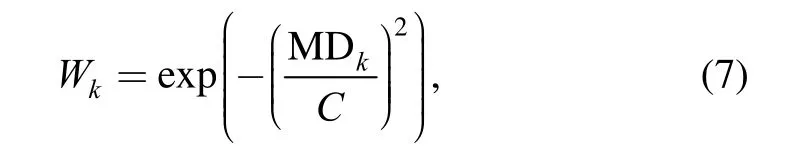
where C is the weight parameter and MDkis defined as the Mahalanobis distance. Based on the correlation between variables, the Mahalanobis distance can identify and analyze the different patterns of the variables. Thus, the problem of scale and correlation inherent in the Euclidean distance is no longer an issue. Given a query input and history data input, the Mahalanobis distance is given by
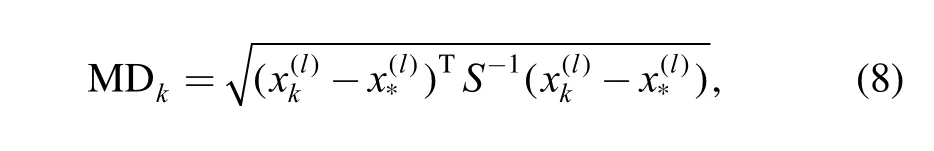
with S the inverse covariance matrix, l the component index of input vectors. Input vectors with higher similarity will be chosen for the training input.
3 Energy Optimization Model
Demand side management(DSM) is used to reduce power consumption/energy cost, while supplying the energy users demand at the same time. We consider a CPS consisting of a single energy provider and several energy consumption devices. In the proposed energy optimization model, the energy provider announces the price of electricity in advance based on the load prediction results.
Suppose the time cycle for the operation of the energy subscribers is divided into K time slots. For each time slot k ∈K , the energy consumed by the users is lk. To design a energy cost model, some assumptions need to be made[22]:
Assumption 1: The energy cost will increase with the addition of energy usage. For every k ∈K ,
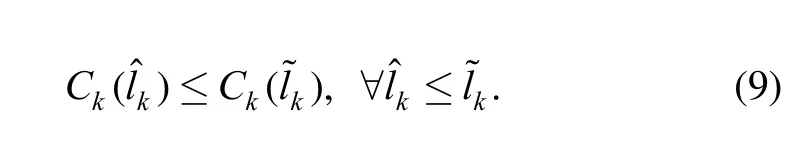
Assumption 2: The energy cost function is strictly convex. Forand
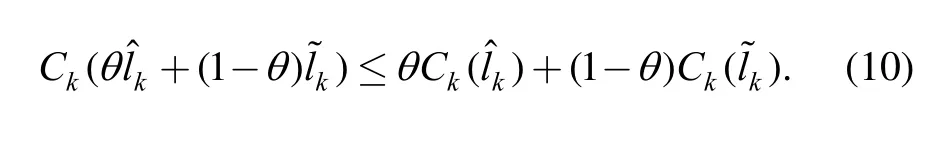
Based on these two assumption, we implement quadratic functions as the energy cost model[22], then calculate the dynamic electricity price as
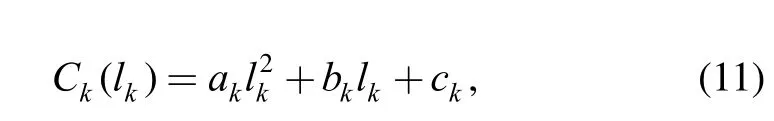
We assume that each CPS energy consuming unit behaves independently, and the energy demand profile of each unit varies according to different parameters, such as time of day, type of the work mode, etc. In this paper, we model the response of the energy consuming units to the dynamic electricity price by implementing the utility function[17]. The utility function reflects the level of satisfaction obtained by the unit. To coincide with the decreasing marginal benefit, we have designed the following utility function:
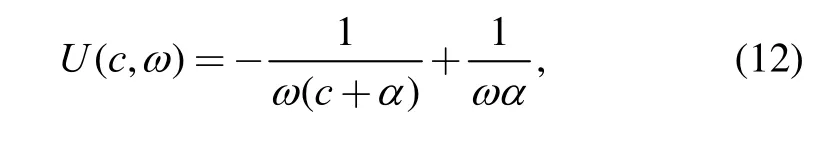
To evaluate the rationality of the user’s energy usage,both the utility function and the cost function should be considered. Thus we introduce the so-called “welfare function” in Ref. [22]:
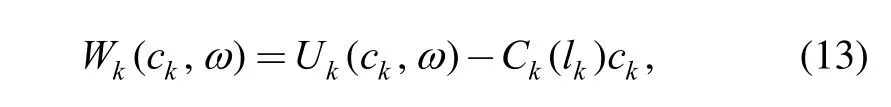
where k ∈ K is a certain time slot,is the utility level of the demand side at that time slotis the energy cost based on the load prediction result, lk,is the energy consumption at that time slot k. In a demand side energy optimization scheme, the user tries to maximize its welfare. In this paper, we introduce the co-evolutionary particle swarm optimization method(CPSO) to deal with this problem.
4 Co-evolutionary Particle Swarm Energy Optimization
Based on the problem optimization formulation in section 3, the aim of the manufacturing center’s DSM is to maximize the welfare function of the system, which is a multi-parameter optimization problem. In this paper, we introduce the co-evolutionary particle swarm optimization method to deal directly with this optimization problem,which can be depicted as
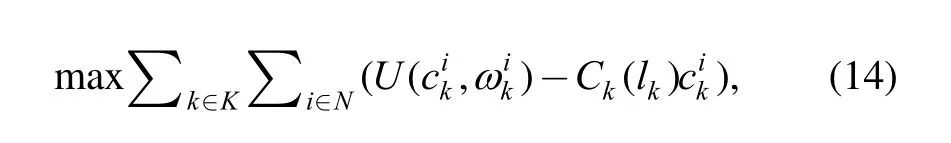
where N denotes the set of all users. We suppose that the energy consumption profile of each unit is inherently fixed while the activation time and operation duration of the units remains to be optimized.
PSO is a swarm-intelligence based optimization technique[23]. In PSO, each particle denotes a potential solution which then flies through the search space to find the optimal solution. Consider a swarm with nsparticles.Letanddenote the local best position and current position of ith particle respectively. The global best position is denoted as pg. Then each particle updates its current velocityiv and positioncip towardlp andcp as follows:
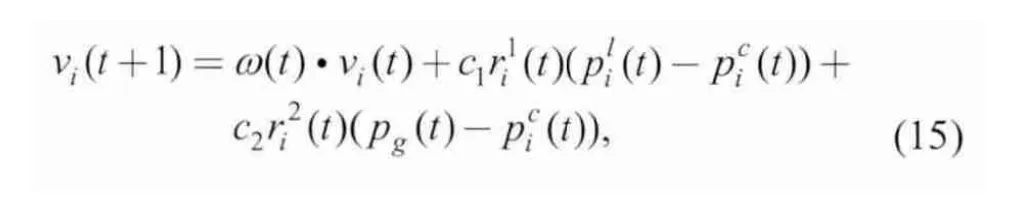
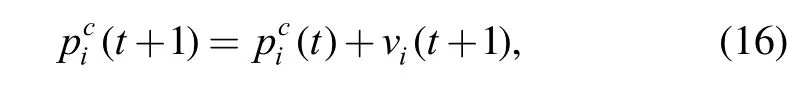
where1c and c2are the acceleration constants,andare random independent variables in the range[0, 1], the inertia weight(t) is used to balance global and local search.

where M is the predefined number of maximum iterations.Then pgandare updated as follows:
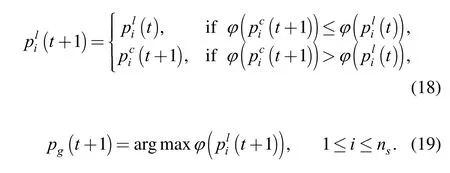
In energy optimization, the load schedule vectoris considered as a particle, where N is the number of energy consuming devices,anddenote the activation time and operation duration of device j, respectively. Normally,the objective function is computed using all the components in the schedule vector, which means that the improvement in some components may overrule a potentially good value for some other components. Unlike standard PSO, in co-evolutionary PSO(CPSO)[23], the search space is partitioned into lower dimensional subspaces by splitting the solution vectors. Then, the optimization of CPSO is implemented with the collaboration ofmn swarms, where each swarm attempts to optimize only the position of one electrical device. Then the global best particles of all the mn swarms are concatenated to form a context vector as required by the objective function. To calculate the fitness of the particles in ith swarm, the other 2 N −2 components in the context vector are kept constant with the values set to the global best particles of the other n−1 swarms. As a result, a significant increase in solution diversity is achieved.
5 Experiment
In this section, we present the experiment results and evaluate the performance of the proposed CPS demand side energy optimization method. Here, a modern machining center possessing dozens of high energy consumption NC machines is recognized as a CPS subsystem. Demand side energy optimization is put into practice for this subsystem. A typical feature of CPS is the implementation of embedded processing devices to monitor and control the physical systems. In this paper, we introduce a distributed advanced metering infrastructure sensing system to monitor the real time working status and energy consumption of each NC machine. In the designed AMI sensing system, the electric energy measuring is executed by smart meters which comply with the standard of DL/T 645–2007. In the system, the data is transfered through a two-way wireless multi-hop communication network using the ZigBee protocol. Information generated by the system’s operating dynamics is collected and transfered to the host while the optimization instructions are fed back to the devices based on the DSM’s strategy. There is a single energy provider for the manufacturing center, and the electric price depends on the predicted electrical demand for the area in which the center is located. Thus, in this CPS subsystem, the end users are enabled by the sensing and control technologies to modify their utilization in a responsive manner which is adaptive to the local energy price dyanmics. The DSM goal is to keep the utilization of the machining system at a relatively high level while reducing the total energy costs.
In the DSM system, the dynamic electric price is one of the key variables for determining energy optimization. In this papaer, we define the energy price as a quadratic function of the predicted electric load based on Eq. (11).We propose a short-term load forecasting scheme to predict the next 24-hour electric demand in a certain region in China, which contains residential, commercial and industrial electrical users. The manufacturing center’s energy costs are submitted to the region’s dynamic energy prices. The forecast procedure is described as follows:
再整合之后,首先是喜剧类型片与爱情类型片,这类喜剧片和爱情片都是以大团圆结局为结尾的影片,作为喜剧片来说,除了剧情和表演幽默有趣,引人发笑之外,其结尾一般会归结为心想事成,万事如意。比如冯小刚导演的《甲方乙方》,它开启了中国贺岁片先河。印象最深的是那个老板,大鱼大肉吃惯了,想去农村呆几天,结果全村的鸡都被他吃了,看到葛优回来了像看见菩萨一样。现在想想,也是,在安逸的生活里呆习惯了,去恶劣的地方真的没法适应。人吧,有些磨难固然是好,体验体验也没啥,但如果真处在那种环境,还是想办法脱离苦海吧,争取向上爬。
(1) Collect the training data for the forecasting model,including historical load, temperature, air humidity, holiday information, etc.
(2) Evaluate the training data using the Mahalanobis distance based Gaussian kernel function. Prune the input data vectors with smaller weight.
(3) Decompose the selected training data into higher and lower frequency components using EMD.
(4) Separate SBL forecasting models can be trained by the two frequency channels, and the forecasting results can become the output as the joint distribution.
The historical data from January 2011 to March 2013 in the selected region in China is collected. It contains the hourly load, dry bulb temperature and dew point, etc. We use the data from January 2011 to February 2013 as the training data and the data from March 1st 2013 to March 31st 2013 to test the forecasting model. Fig. 1 shows the 24-hour load forecasting results of the proposed componential weighted sparse Bayesian learning model.The forecasting date is Mach 3rd, 2013.
One of the advantage of the SBL forecasting method is the availability of the probability distribution of the forecasting results. Fig. 1 shows that the actual electrical load has been embraced by the forecasted ±3region,which means that the forecasting method is quite robust.
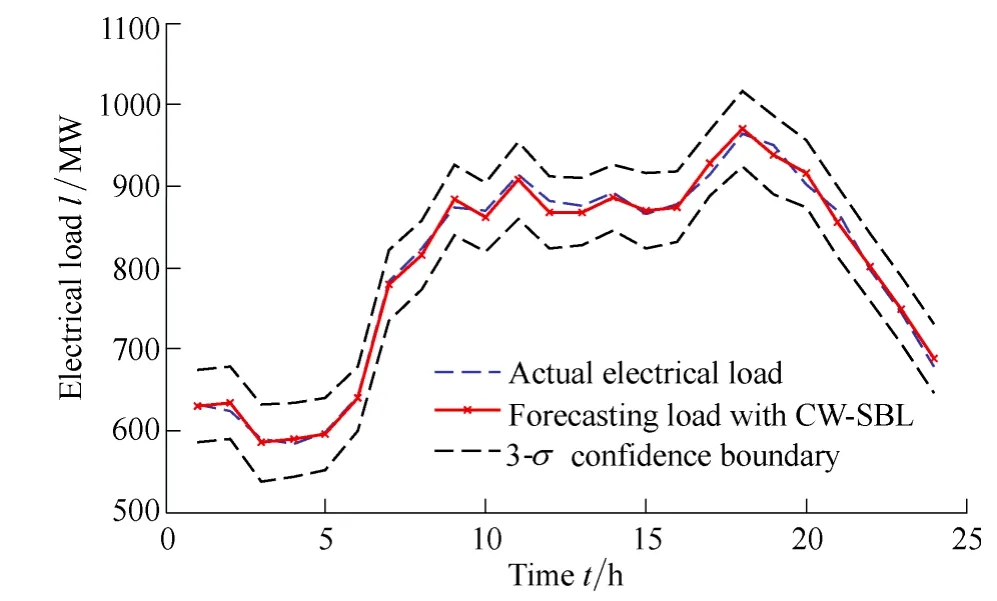
Fig. 1. 24-hour load forecasting result of March 3rd, 2013
We continuously forecasted the 24-hour electrical load for 1 month, from March 1st to March 31st, 2013. To inspect the improvement in the CW-SBL, we compared the original SBL model(SBL) and the SBL with Mahalanobis distance based Gaussian weighting(W-SBL). Then we evaluated the three forecasting models with mean absolute error(MAE), mean absolute percentage error(MAPE),normalized mean square error(NMSE), and relative error percentage(REP). The results are shown in Table 1. Where we can see that the CW-SBL has the highest prediction accuracy compared to the W-SBL model and the original SBL model. The forecast error has been significantly reduced.

Table 1. Evaluation of different forecasting models
The example in Fig. 2 shows that when the peak load is anticipated, the electricity price is reasonably higher (such as from 18:00 to 20:00) while the price is relatively lower at midnight when fewer electrical devices are active.
In section 3, we pointed out that the parameterof the utility function could be changed due to the type of energy users or time of day. Fig. 3. gives the different utility energy user functions. We assume that under the condition of consuming the same energy, the utility value increases the most during work hours (from 8:00 to 18:00), while in the evening (from 18:00 to 24:00), it takes second place,and midnight (from 00:00 to 6:00) takes the last place. So we use the utility function at=0.4 for the work hours,utility function at=0.8 and=1 (depends on the working statues of the NC machine) for the evening and midnight respectively. In view of the random event during the manufacturing process, we assume thatfollows a normal distribution.
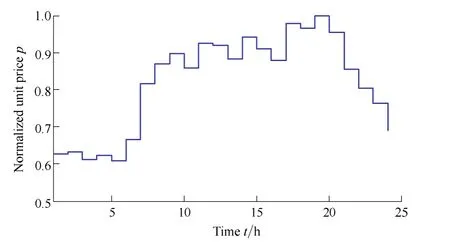
Fig. 2. Dynamic electricity price of Mar 3rd, 2013
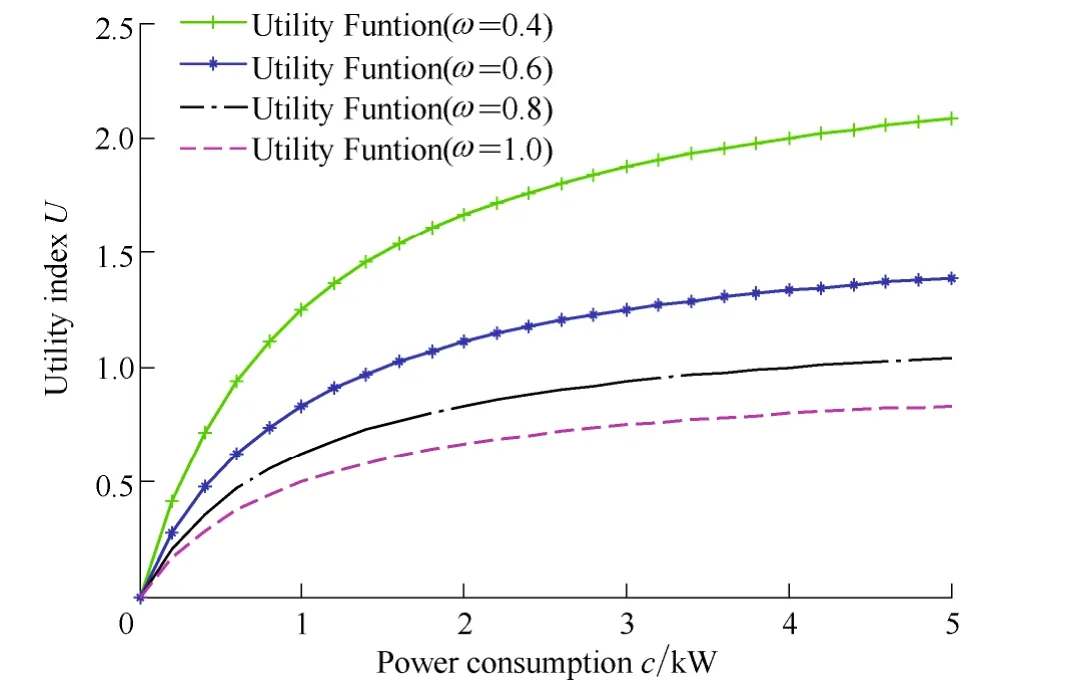
Fig. 3. Different utility functions for energy users ( =1 )
The demand side energy optimization scheme is carried out for the machining center, which possesses 10 DMG CTX310 NC machines. We envision a situation where each NC machine has two operating styles. The power consumption profile for each operating style is given in Fig. 4.
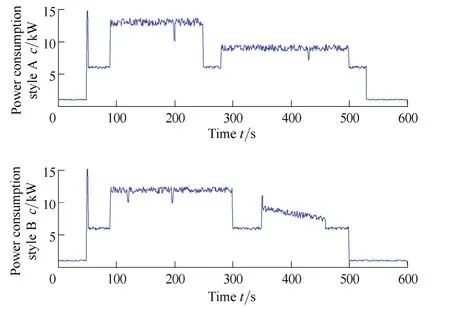
Fig. 4. Power consumption profile of different operation style
Here we can simplify the profile by filtering the high frequency disturbance. Then the operation energy consumption is recognized as an addition of square wave and triangular wave, which may reduce the computational complexity. For each NC machine in the center, we consider thatfollows a normal distribution in order to reflect the random statues of the devices.
Both the PSO and the CPSO algorithms are used to optimize the manufacturing center’s demand side energy usage with the goal of maximizing the system’s aggregate welfare function. The optimization results are given in Fig.5 and Fig. 6.
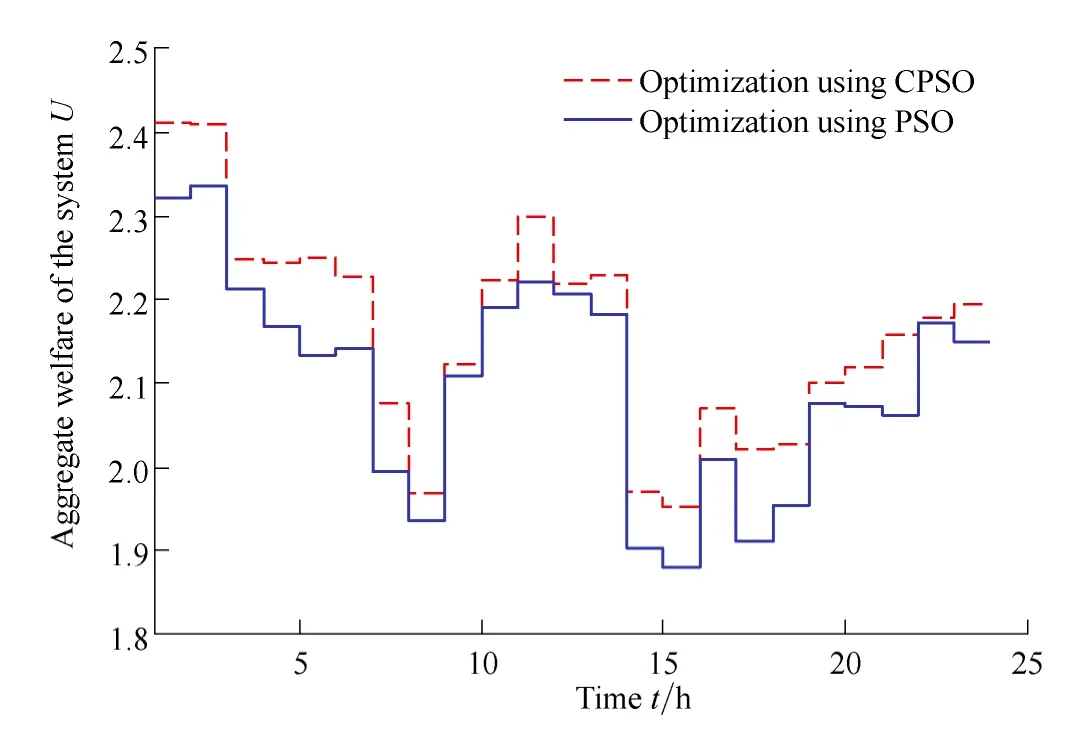
Fig. 5. Aggregate utility of the system on March 3rd, 2013
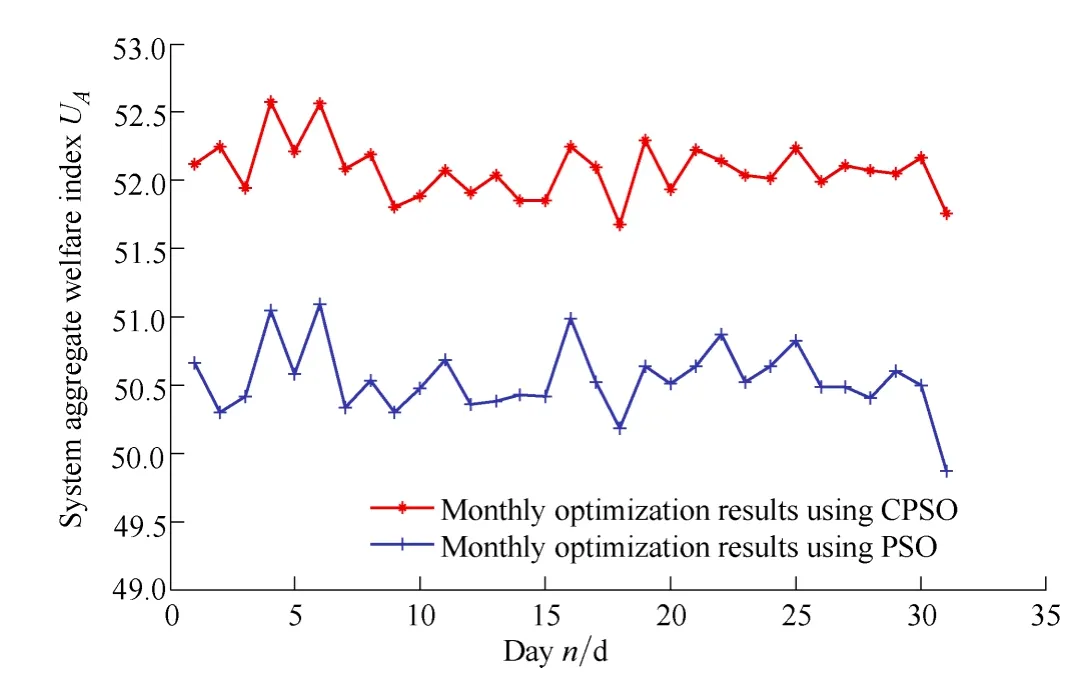
Fig. 6. Aggregate welfare of a month(March, 2013)
Fig. 5 gives the 24-hour optimization results, which shows that during the peak load period from 8:00 to 10:00 or 15:00 to 19:00, the system’s welfare value is at its lowest level of the day because of the high electricity prices. In contrast, during the period from 9:00 to 14:00 has a relatively higher welfare value owing to its lower dynamic price and relatively higher utility value. The welfare value reaches its peak around midnight, which can be attributed mainly to the lower electricity price. Fig. 6 shows the monthly optimization results. We can see that, compared to PSO, CPSO can improve the average welfare value by 4%,while both methods are robust in time span and can be self-adaptive to dynamic price and user demand.
6 Conclusions
(1) The proposed componential weighted sparse Bayesian learning could predict the short term electrical load effectively and robustly. Compared with traditional sparse Bayesian learning forecasting method, the proposed method could enhance the accuracy by about 4.3% (REP).
(2) A manufacturing center is recognized as a subsystem of the cyber physical systems. The employing of the load prediction-based pricing strategy for the CPS could introduce cost control demand into the control strategies.
(3) The energy utility and welfare function are used as the optimization objective of the manufacturing center.Both PSO and CPSO based methods are developed to minimize the total energy cost while guaranteeing the service quality of the cyber physical systems. Experiment results show that the CPSO method could raise the benefit of optimization by 5%.
[1] ILIC M D, LE X, KHAN U A, et al. Modeling of future cyber-physical energy systems for distributed sensing and control[J].IEEE Transactions on Systems, Man and Cybernetics-Part A:Systems and Humans, 2010, 40(4): 825–838.
[2] MACANA C A, QUIJANO N, MOJICA-NAVA E. A survey on cyber physical energy systems and their applications on smart grids[C]//IEEE PES Conference on Innovative Smart Grid Technologies, Medellin, Colombia, October 19–21, 2011: 1–7.
[3] LOGENTHIRAN T, SRINIVASAN D, TAN Zongshun. Demand side management in smart grid using heuristic optimization[J].IEEE Transactions on Smart Grid, 2012, 3(3): 1244–1252.
[4] SUN Dongye, LIN Xinyou, QIN Datong, et al. Power-balancing instantaneous optimization energy management for a novel series-parallel hybrid electric bus[J]. Chinese Journal of Mechanical Engineering, 2012, 25(6): 1161–1170.
[5] TONG Liang, YAN Ping, LIU Fei. Monitoring computer numerical control machining progress based on information fusion[J]. Chinese Journal of Mechanical Engineering, 2011, 24(6): 1074–1082.
[6] HE Yan, LIU Fei. Methods for integrating energy consumption and environmental impact considerations into the production operation of machining processes[J]. Chinese Journal of Mechanical Engineering, 2010, 23(4): 428–435.
[7] XU Ming, JIN Bo, YU Yaxin, et al. Using artificial neural networks for energy regulation based variable-speed electrohydraulic drive[J].Chinese Journal of Mechanical Engineering, 2010, 23(3): 327–335.
[8] KAH-HOE N, SHEBLE G B. Direct load control: a profit-based load management using linear programming[J]. IEEE Transactions on Power Systems, 1998, 13(2): 688–694.
[9] HSU Y Y, SU C C. Dispatch of direct load control using dynamic programming[J]. IEEE Transactions on Power Systems, 1991, 6(3):1056–1061.
[10] WU Qiuwei, WANG Peng, GOEL L. Direct load control(DLC)considering nodal interrupted energy assessment rate(NIEAR) in restructured power systems[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1449–1456.
[11] BHATTACHARYYA K, CROW M L. A fuzzy logic based approach to direct load control[J]. IEEE Transactions on Power Systems,1996, 11(2): 708–714.
[12] VAN DEN BERGH F, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 225–239.
[13] WANG Xue, WANG Sheng, MA Junjie. An improved co-evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment[J]. Sensors, 2007, 7(3):354–370.
[14] HUANG C M, HUANG C J, WANG M L. A particle swarm optimization to identifying the ARMAX model for short-term load forecasting[J]. IEEE Transactions on Power Systems, 2005, 20(2):1126–1133.
[15] LIN C J, CHEN C H, LIN C T. A hybrid of cooperative particle swarm optimization and cultural algorithm for neural fuzzy networks and its prediction applications[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews,2009, 39(1): 55–68.
[16] ZHANG Yun, ZHOU Quan, SUN Caixin, et al. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment[J]. IEEE Transactions on Power Systems, 2008,23(3): 853–858.
[17] MATTEO D F, YAO Xin. Short-term load forecasting with neural network ensembles: a comparative study[J]. IEEE Computational Intelligence Magazine, 2011, 6(3): 47–56.
[18] CHEN Ying, LUH P B, CHE G, et al. Short-term load forecasting:similar day-based wavelet neural networks[J]. IEEE Transactions on Power Systems, 2010, 25(1): 322–330.
[19] KHOSRAVI A, NAHAVANDI S, CREIGHTON D, et al. Interval type-2 fuzzy logic systems for load forecasting: a comparative study[J]. IEEE Transactions on Power Systems, 2012, 27(3):1274–1282.
[20] TIPPING M E. Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001(1):211–244.
[21] HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London-Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995.
[22] SAMADI P, MOHSENIAN R A H, SCHOBER R, et al. Optimal real-time pricing algorithm based on utility maximization for smart grid[C]//2010 1st IEEE International Conference on Smart Grid Communications, Gaithersburg, USA, October 4–6, 2010: 415–420.
[23] WANG Xue, WANG Sheng. Hierarchical deployment optimization for wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2011, 10(7): 1028–1041.
猜你喜欢
杂志排行
Chinese Journal of Mechanical Engineering的其它文章
- Theoretical Analysis and Experimental Verification on Valve-less Piezoelectric Pump with Hemisphere-segment Bluff-body
- Carbody Structural Lightweighting Based on Implicit Parameterized Model
- Effectiveness of a Passive-active Vibration Isolation System with Actuator Constraints
- Numerical Simulation and Analysis of Power Consumption and Metzner-Otto Constant for Impeller of 6PBT
- Proceeding of Human Exoskeleton Technology and Discussions on Future Research
- A Novel Estimating Method for Steering Efficiency of the Driver with Electromyography Signals
