Analysis of the Flow Rate Characteristics of Valveless Piezoelectric Pump with Fractal-like Y-shape Branching Tubes

HUANG Jun, ZHANG JianHui, , WANG ShouYin, and LIU WeiDong

1 State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

2 Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

1 Introduction

In recent years, with advancement of manufacturing and processing technology, especially in micro electronic mechanical system (MEMS), information technology (IT)industry has been developing rapidly and integration of various types of chips has also been greatly improved.However, highly integrated chips inevitably bring with problem of heat accumulation, which has seriously affected the efficiency of the chip. At the same time, the conventional solution of forced-air convection heat transfer is trending to its limit. To improve the efficiency of the chips, new heat dissipation methods have become a research focus for those highly integrated chips[1–5].

Microchannel heat sink with high heat transfer coefficients and simple manufacturing has been extensively investigated due to its wide application prospective in electronic cooling. TUCKERMAN, et al[6], carried out pioneering work for the first proposed microchannel cooling technology in 1981. PENG, et al[7], performed experimental investigations on the convective heat transfer and flow characteristics of water in microchannel structures with small rectangular channels in 1996. Based on constructal theory, BEJAN, et al[8], firstly proposed the tree network to be used for electronic cooling in 1997. PENCE[9]proposed a fractal-like branching flow network to improve the thermal efficiency and temperature uniformity of the heat sink in 2000. CHEN, et al[10], studied fractal tree like microchannel networks in 2002. They found that the fractal tree like microchannel network can improve convective heat transfer and hydrodynamic performance of the heat sink compared with the conventional parallel microchannel network. XU, et al[11], analyzed the heat conduction through symmetric fractal tree-like branching networks and obtained the expression of thermal conductivity in the networks in 2006. Meanwhile, they analyzed the relationship between the effective thermal conductivity and the geometric structures of the networks. However, so as for the cooling system, the microchannel still need a separate micropump as an external power source, which makes the system difficult to miniaturization, and also affects its reliability.

One new type microchannel cooling system with the characteristic of simple structure and high reliability,combinating power source and microchannel effectively,needs to be designed to overcome above shortcomings.According to the preliminary studies and valve-less piezoelectric pump with Y-shape tubes invented by ZHANG, et al[12–13], the valve-less piezoelectric pump with fractal-like Y-shape branching tubes (VPPFYT) will be proposed. Fractal-like Y-shape branching tube (FYBT) is a no-moving-part (NMP) valve among the valve-less piezoelectric pump, meanwhile pump body and power source can be integrated on the chip.

Size of fractal dimension reveals complexity of geometry.Hence, fractal theory will be used to discuss flow resistance characteristics of FYBTs with different hydraulic diameter ratios, and analyze relationships between flow rate of VPPFYT and fractal dimensions of diameter distribution of the tubes in this study.

This paper will firstly propose valveless piezoelectric pump with fractal-like Y-shape branching tubes. It is designed based on actuating mechanism, considering the integration of fractal-like branching tube in microchannel heat sinks, and pump body also. Then, expressions of flow resistance of the tube along merging and dividing flows are established respectively, by which the relationships between flow resistance of FYBT and pump flow rate are analyzed. Meanwhile, finite element method is employed to analyze the FYBTs with different fractal dimensions of diameter distribution. The relationships between pressure drop and flow rate along merging and dividing flows are obtained. Finally, experimental study is done, the feasibility of the VPPFYT is validated, and variations of pump flow rate influenced by fractal dimension of diameter distribution and electrical parameter are obtained.

2 Structure of the Fractal-like Y-shape Branching Tube and Pump

Fig. 1 shows the structure of the fractal-like Y-shape branching tube. According to structure of fractal-like branching and based on the Y-shape tube, the fractal-like Y-shape branching tube is designed. To generate this tube,0th level mother duct is divided into 2 daughter branches at 1th level. The branches at the ends of the newly formed ducts may be continued until the required FYBT at the specified branching level is obtained. The width of the 0th level mother duct is w0, the length is l0, then wkis the width at the kth branching level, and lkis the length at the kth branching level. Each bifurcation angle is 2α, and the depth of the whole tube is h.

When the flow happens in the FYBT, the flow resistance of merging flow is unequal to that of dividing flow.Therefore, a pair of fractal-like Y-shape branching tubes as NMP valve is installed on each side of pump chamber,which constructs the valveless piezoelectric pump with fractal-like Y-shape branching tubes, as shown in Fig. 2.This pump is mainly composed of a piezoelectric vibrator,a pump chamber and a pair of fractal-like Y-shape branching tubes headed in the same direction.

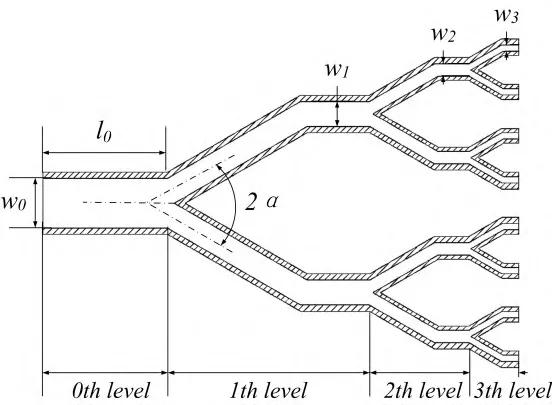
Fig. 1. Fractal-like Y-shape branching tube

Fig. 2. Valveless piezoelectric pump with fractal-like Y-shape branching tubes

Fig. 3 is a schematic diagram of VPPFYT achieving heat dissipation. The substrate with the fractal-like Y-shape branching microchannels is bonded to the chip, on which cover plate is packaged. Piezoelectric thin film and electrode are formed by method of sputter deposition on the surface of cover plate, which assemble a piezoelectric vibrator. The piezoelectric vibrator loaded by an alternating voltage will vibrate upwards and downwards causing the coolant movement. As the result of the difference flow resistances between the merging and dividing flows, the coolant flows from inlet of pump towards the outlet in macro continuously. Meanwhile, fractal-like Y-shape branching tubes have the characteristics of high heat transfer efficiency and better temperature uniformity, which can transfer the heat of chip with the coolant movement.Therefore, by integrating the cooling microchannel and power source, this pump greatly reduces the volume of the whole cooling system.

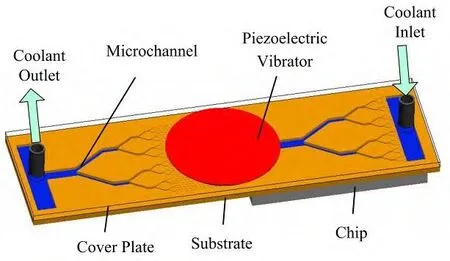
Fig. 3. Valveless piezoelectric pump with fractal-like Y-shape branching tubes on chip

3 Theoretical Analysis for the Flow Resistance and Pump Rate

3.1 Flow resistance of fractal-like Y-shape branching tube

Fig. 1 shows that, wkand lkrepresent the width and length of the kth level duct, respectively. And kth level mother duct is divided into 2kdaughter branches at (k+1)th level. Two scale factors are defined to describe the geometric structure of branching network.

where l0and d0are the length and hydraulic diameter of the initial (0th level) mother duct, respectively. lmand dmare the length and hydraulic diameter of the terminal (mth level)daughter duct, respectively. According to the fractal characteristics of the structure[14],

where Dland Ddis the fractal dimensions of length and diameter distribution of the fractal-like Y-shape branching network, respectively. For the structure of two bifurcations,n=2. Eq. (5) can be presented as follows:

Due to characteristics of difference resistances between merging and dividing flows, fractal-like Y-shape branching tube is exploited as a NMP of valveless piezoelectric pump.

When fluid dividing through tube, the pressure drop along the duct at the kth branching level is given by

where vkis the velocity in the kth branching level duct,and c is a constant, which depends on fluid properties and cross sectional shape of the duct.

The local pressure loss, caused by fluid dividing through tube from (k−1)th level to kth level , can be indicated as:

where ξ is the local resistance coefficient when fluid dividing through tube. The bifurcation angles of Y-shape tubes in every level are 2α, thus the local resistance coefficient of every bifurcation is equal.

From the law of mass conservation,

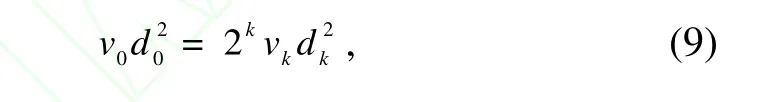
Thus, when the fluid flows along dividing direction, the total pressure drop of the whole tube can be expressed as:

From Eqs. (6) and (10),

The total flow resistance of the fractal-like Y-shape branching tube, when fluid dividing through the tube, is

Similarly, when the fluid flows along merging direction,the pressure drop along the duct at the kth branching level is given by

The local pressure loss, caused by fluid merging through tube from kth level to (k−1)th level, is expressed as:

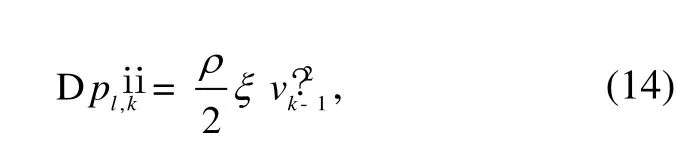
where ξ¢ is the local resistance coefficient when fluid merging through the tube.

Thus, when the fluid flows along merging direction, the total pressure drop of the whole tube is obtained:

The total flow resistance of the fractal-like Y-shape branching tube, when fluid merges through the tube, is

3.2 Flow rate analysis

Micropump efficiency is evaluated for two limit loading conditions: maximum pressure head at zero flow rate and maximum flow rate at zero pressure head. When piezoelectric pump exports maximum flow rate, pressure drops in two NMP valves are equal[15], as shown in Fig. 4.

The algebraic sum of flow rates, either flow into or out off the pump chamber through FYBT, is equal to the amount of fluid in pump chamber. So,

Fig. 4. Flowing scheme of the valveless piezoelectric micropump with fractal-like Y-shape branching tube

The maximum flow rate of the piezoelectric pump can be expressed as

From Eqs. (12) and (16),

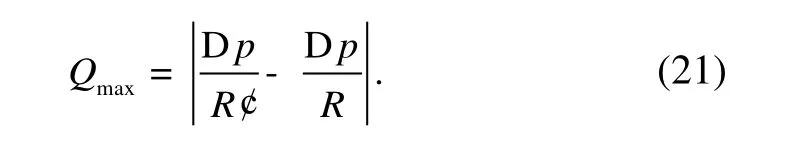
When piezoelectric vibrator is driven under a certain frequency, the maximum flow rate of the pump depends on branching levels, fractal dimensions of length and diameter distribution and the local resistance coefficient of the tube.So,

This nonlinear flow resistance in Eqs. (12) and (16),caused by local pressure loss, does not only depend on the local resistance coefficient and the fractal dimensions of diameter distribution of the tube, but also relate to the flow rate. Therefore, the study utilized the finite element method to analyze the relationship between the flow rate and the pressure drop in the FYBT with different fractal dimensions of diameter distribution is conducted, so that critical standard of effectiveness can be judged.

4 Simulation Analysis

In this research, the software CFX is employed to perform the finite element analysis. The model of fractal-like Y-shape branching tube is established, and the duct width of each level is obtained, as shown in Table 1.

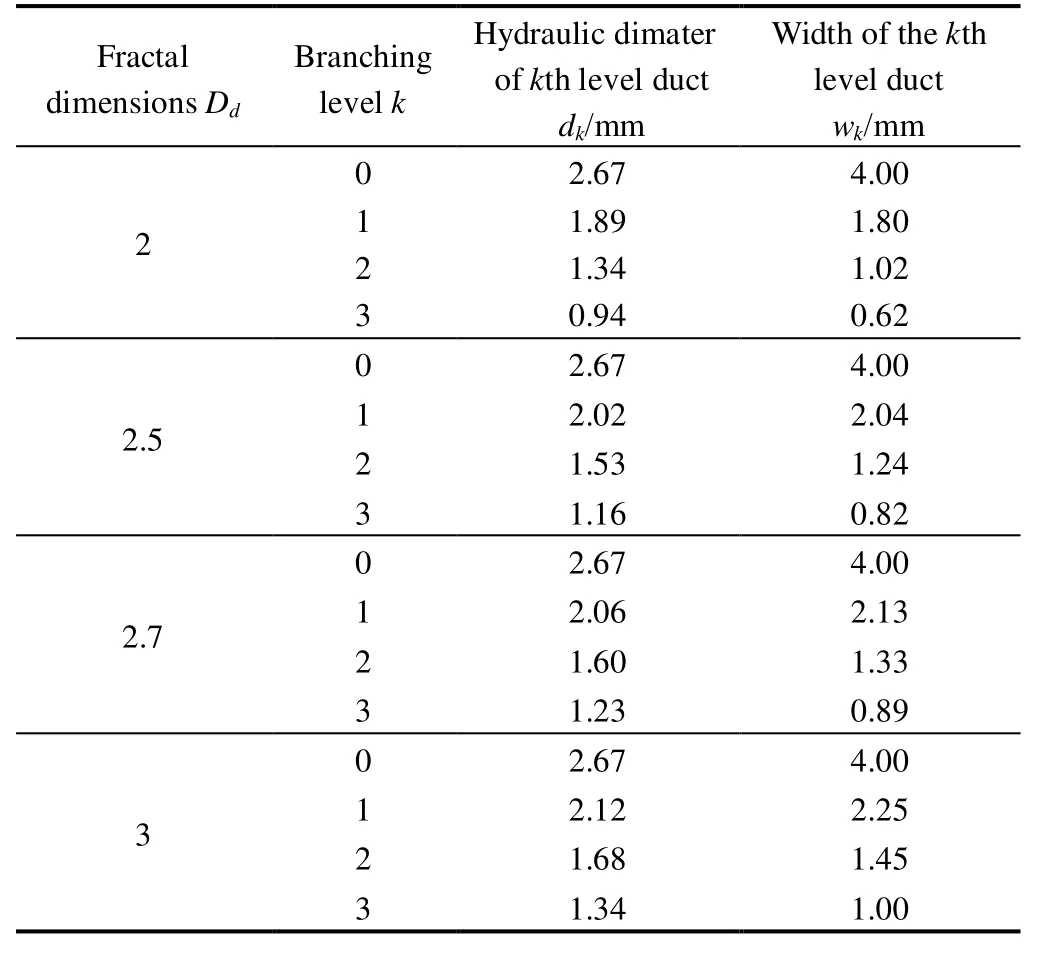
Table 1. Duct widths of each level with different fractal dimensions of diameter distribution

The model of fractal-like Y-shape branching tube is imported into finite element software, and its flow field is simulated with water as the working fluid. Due to the micro amplitude of vibration of piezoelectric vibrator, the flow is assumed to be laminar in this research. No-slip boundary conditions are applied at the FYBT surfaces. The overall pressure drop across the tube is defined as D p = pin- pout,where pinand poutare the inlet and outlet pressures,respectively. The reference pressure (atmosphere pressure)as the outlet pressure is loaded the outlet planes[16].

The relationship between pressure drop and flow rate in the tube when flow is merging and dividing can be obtained respectively. Fig. 5 is velocity and pressure contour pattern of the tube along merging and dividing flows, when Dd=2,D p=20 Pa.

Fig. 5. Velocity and pressure contour patterns of the fractal-like Y-shape branching tube, when

Fig. 6 and Fig. 7 show the relationship curves between pressure drop and flow rate of the FYBT along merging and dividing flows respectively.

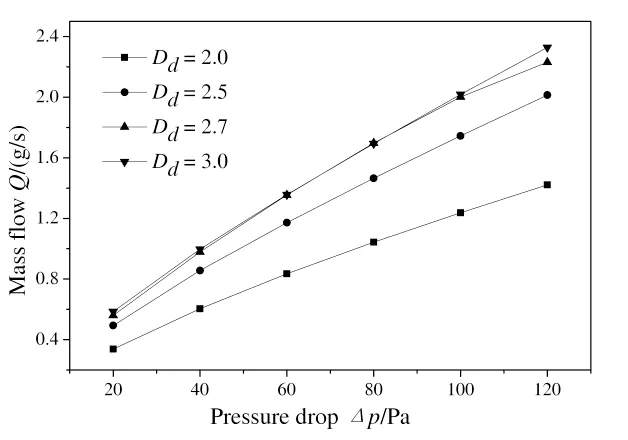
Fig. 6. Curves between pressure drop and mass flow of the tube along dividing flow

Fig. 7. Curves between pressure drop and mass flow of the tube along merging flow

Simulation results show that, with pressure drop increase,export flow rate of tubes with different fractal dimensions of diameter distribution increases gradually. When pressure drop is fixed, with fractal dimensions of diameter distribution increase, export flow rate of tubes increase as well. Meanwhile, export flow rate of each tube is unequal for merging and dividing flows. According to Eq. 20, when difference of flow rate along merging and dividing flows becomes larger, the flow rate of the VPPFYT increases.

5 Experimental Study

Four VPPFYTs with different fractal dimensions of diameter distribution are fabricated, as shown in Fig. 8. The geometrical parameters of each tube are the same with Table 1.

Fig. 9 represents a picture of flow measurement for the valveless piezoelectric pump with fractal-like Y-shape branching tubes. The piezoelectric pump is driven by an alternating sine-wave input. The input signal within 100 V peak to peak (VP-P) is controlled by a function generator[17].The liquid in the piezoelectric pump is deionized water.Through measuring the mass flow rate of VPPFYT in unit time by changing driving frequency of the piezoelectric vibrator, we can obtain the experimental results of volume flow rate with changing frequency under 100 VP-P. The results about the flow rate versus driving frequency are shown in Fig. 10.

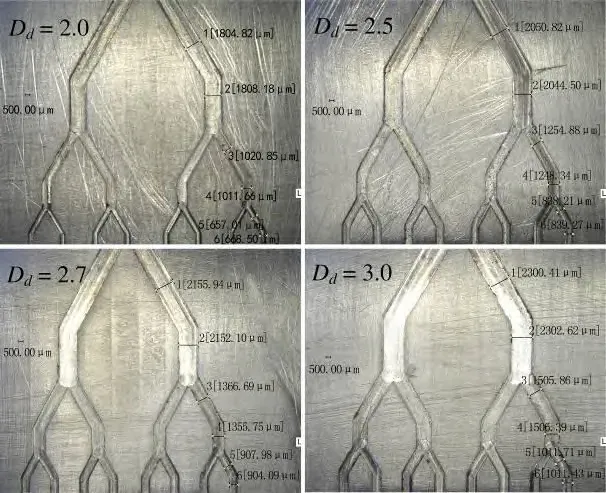
Fig. 8. Tubes with different fractal dimensions of diameter distribution

Fig. 9. Schematic diagram of flow rate experiment

The results show that the experimental result is in keeping with the result of simulation. With fractal dimensions of diameter distribution increases, the difference of flow resistance of FYBT along merging and dividing direction increase, which brings a larger flow rate of the pump. When Dd=3, the maximum flow rate of the valveless pump is 29.16 mL/min under 13 Hz.

When the driving frequency is 13 Hz, we can obtain the curves of flow rate versus voltage of the pump with changing driving voltage of the piezoelectric vibrator as shown in Fig. 11. This figure demonstrates that flow rate of pump increase as driving voltage enhances. When Dd=3,the maximum flow rate of the valveless pump is 55.92 mL/min under 200 VP-P(13 Hz).

Fig. 11. Curves between the flow rate and the driving voltage

The experiments show the effectiveness of valveless piezoelectric pump with fractal-like Y-shape branching tubes, which prove that fractal-like Y-shape branching tube has different flow resistances in merging and dividing directions.

6 Conclusions

(1) The relationship between structure and flow resistance of fractal-like Y-shape branching tube is analyzed based on the fractal theory. Meanwhile, the flow rate characteristics of valveless piezoelectric pump with fractal-like Y-shape branching tubes are analyzed. When piezoelectric vibrator is driven under a certain frequency,the maximum flow rate of the pump depends on branching levels, fractal dimensions of length and diameter distribution and the local resistance coefficient of the tube.

(2) The finite element software is employed to simulate the flow filed of fractal-like Y-shape branching tube. And the relationships between pressure drop and flow rate of FYBT with different fractal dimensions of diameter distribution are obtained.

(3) The valveless piezoelectric pumps with different fractal dimensions of diameter distribution are designed and fabricated. The relationships between the driving frequency and the flow rates, as well as the relationships between the driving voltage and the flow rates are experimentally investigated. The experimental results show that, with fractal dimension of diameter distribution increases, the flow rate of the pump increases. When Dd=3,the maximum flow rate of the valveless pump is 29.16 mL/min under 100 VP-P(13 Hz) power supply.

[1] SINGHAL V, GARIMELLA S V, RAMAN A. Microscale pumping technologies for microchannel cooling systems[J]. Applied Mechanics Reviews, 2004, 57(3): 191–221.

[2] MA H K, CHEN B R, GAO J J, et al. Development of an OAPCP-Micropump Liquid Cooling System in a Laptop[J].International Communications in Heat and Mass Transfer, 2009,36(3): 225–232.

[3] XIAO Qinghua, CHEN Lingen, SUN Fengrui. Constructal entransy dissipation rate and flow-resistance minimizations for cooling channels[J]. Sci. China Tech. Sci., 2010, 53(9): 2458–2468.

[4] CHI Yong, TANG Yong, CHEN Jinchang, et al. Miniaturized capillary pumped loop heat controlling system and it’s manufacturing technique[J]. Chinese Journal of Mechanical Engineering, 2007, 43(12): 166–170. (in Chinese)

[5] LI Yong, HE Ting, ZENG Zhixin. Analysis of collapse in flattening a micro-grooved heat pipe by lateral compression[J]. Chinese Journal of Mechanical Engineering, 2012, 25(6): 1210–1217.

[6] TUCKERMAN D B, PEASE R F W. High-performance heat sinking for VLSI[J]. IEEE Electron Device Letters, 1981, 2(5): 126–129.

[7] PENG Xiaofeng, PETERSON G P. Convective heat transfer and flow friction for water flow in microchannel structures[J]. Int. J.Heat Mass Transfer, 1996, 39(12): 2599–2608.

[8] BEJAN A, ERRERA M R. Deterministic tree networks for fluid flow: geometry for minimal flow resistance between a volume and one point[J]. Fractals, 1997, 5(4): 685–695.

[9] PENCE D V. Improved thermal efficiency and temperature uniformity using fractal-like branching channel networks[C]//Proceedings of the International Conference on Heat Transfer and Transport Phenomena in Micro Scale. Banff, Canada,2000: 142–148.

[10] CHEN Yongping, CHENG Ping. Heat transfer and pressure drop in fractal tree-like microchannel nets[J]. Int. J. Heat Mass Transfer,2002, 45(13): 2643–2648.

[11] XU Peng, YU Boming, YUN Meijuan, et al. Heat conduction in fractal tree-like branched networks[J]. Int. J. Heat Mass Transf.,2006, 49(19–20): 3746–3751.

[12] ZHANG Jianhui, LI Yili, XIA Qixiao. Analysis of the pump volume flow rate and tube property of the piezoelectric valveless pump with Y-shape tubes[J]. Chinese Journal of Mechanical Engineering, 2007,43(11): 136–141. (in Chinese)

[13] ZHANG Jianhui, LU Jizhuang, XIA Qixiao, et al. Application of valve-less piezoelectric pump with Y-shape tubes for transporting cells and macromolecule[J]. Chinese Journal of Mechanical Engineering, 2008, 44(9): 92–99. (in Chinese)

[14] MANDELBROT B B. The fractal geometry of nature[M]. New York,W. H. Freeman and Company, 1982.

[15] IZZO I, ACCOTO D, MENCIASSI A, et al. Modeling and experimental validation of a piezoelectric micropump with novel no-moving-part valves[J]. Sens. Actuators A, 2007, 133(1): 128–140.

[16] XIA Qixiao, ZHANG Jianhui, LEI Hong, et al. Analysis on flow field of the valveless piezoelectric pump with two inlets and one outlet and a rotating unsymmetrical slopes element[J]. Chinese Journal of Mechanical Engineering, 2012, 25(3): 474–483.

[17] WANG Baowei, CHU Xiangcheng, LI Enzhu, et al. Simulations and analysis of a piezoelectric micropump[J]. Ultrasonics, 2006, 44:643–646.