基于概率理论的折线形滑坡锚固结构受力

徐鸿彪，叶尚其，刘汉香

（1.四川省交通运输厅公路规划勘察设计研究院，成都 610041；2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610051）

1 前言

岩土锚固技术作为一种支护技术，具有深层加固、随机补强等特点［1]，结合预应力技术时还具有主动加固的性能，近年来在滑坡治理中被广泛的运用。传统斜坡锚固技术多用于岩质边坡预加固或岩质滑坡治理上。由于常规锚头多为孤立的点状，对岩土体产生较大的冲切力，在松散岩土体中易形成锚固失效。近年来，随着锚固结构在这一类斜坡中的作用机理研究逐渐深入［2]，针对锚头对松散岩土体的冲切破坏问题，提出采用地梁、格框替代传统的点状锚头，具有显著的可行性［3－6]。这些研究工作大力促进了锚固结构在滑坡治理中的应用。

在设计锚固结构时，对于直线形滑坡（滑面为规则的直线），有现行的方法［7]及规范［8]可以直接利用。对于近年来更为常见的折线形滑坡（滑面呈不规则线形），目前工程上仍主要采用试算法进行，即先计算锚固结构的最大抗力，其次对坡面进行锚固系统的布置，再计算当锚固力分别作用于与锚杆、锚索相交滑面所在滑块及锚头所在滑块时的稳定性系数，当二者之间的低值小于规范要求的安全系数时，需调整锚固结构或锚固系统的布置后重新设计。这种方法带有主观随意性，且不符合先计算外力再行结构设计这一基本的结构设计方法流程。当滑面极不规则时，会使设计工作量大大增加。不少学者针对折线形滑坡的锚固设计方法，尝试从不同的角度进行了改进。刘才华［9]等以拟设置锚索的主下滑段为研究对象，虽还是以传递系数法为基础，但并不要求边坡在各加固段条块的剩余下滑力为0，而只需加固段最后一条块的剩余下滑力不超过阻滑力即可。由此在保证边坡稳定性满足要求的条件下，得到了预应力锚索布置间距与其设计荷载的关系，且不需要进行反复验算。蒋楚生［10]等则利用 Morgenster n－Price法，对已施加锚固力的滑坡体各滑块三个平衡公式进行迭代计算，直至满足滑体稳定性系数小于安全系数。

本文从锚固结构的受力计算方法出发，在分析了直线形滑坡锚固体系与滑面倾角关系的基础上，从概率学的角度出发，引入折线形滑坡锚固结构的最大概然入射线、期望角两个概念，避免了试算法中需要尝试代入不同段滑面的倾角进行多次运算才能满足稳定性要求的繁复工作，将折线形滑坡锚固结构受力计算转变为直线形滑坡锚固结构受力计算，并建立应用该方法进行折线形滑坡锚固力计算的一般流程，以期为折线形滑坡的锚固力计算提供一定参考。

2 直线形滑坡锚固体受力计算方法

假定有一处采用锚固体系处治的直线形滑坡，锚固体系全部布设于滑面所对应的坡面锚固范围1内，如图1所示。

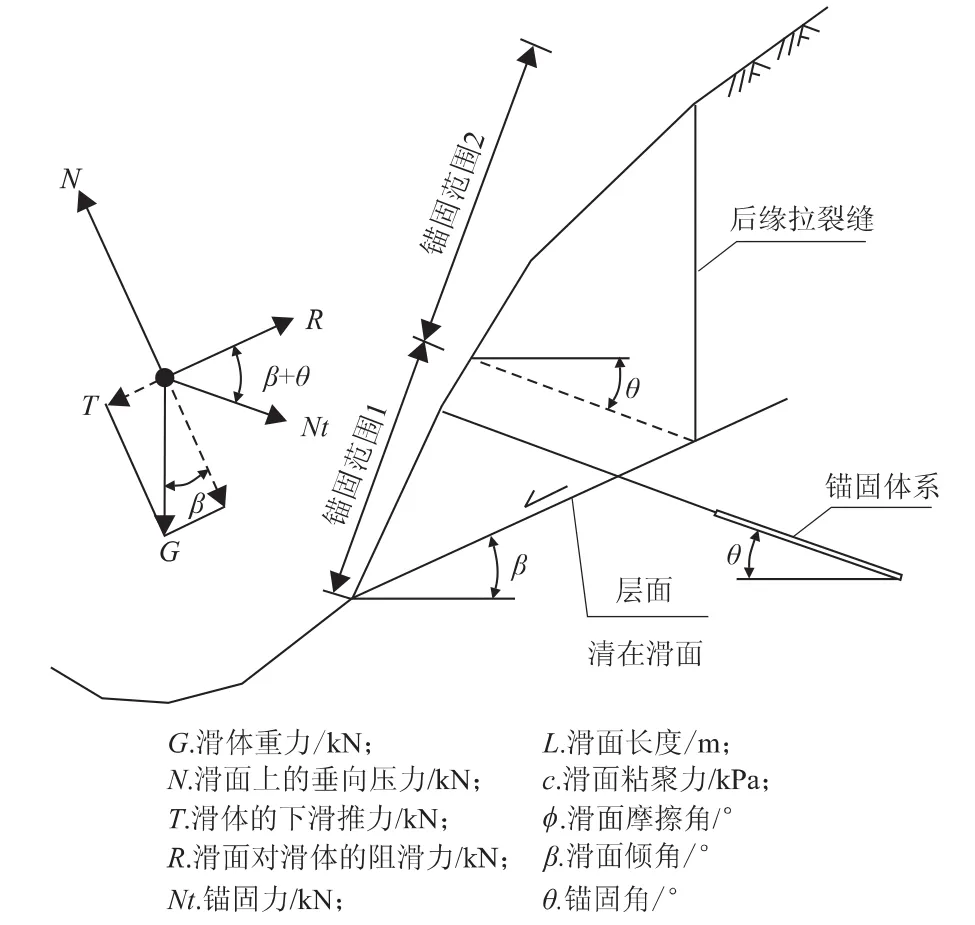
图1 直线形滑坡锚固系统计算简图Fig.1 Calculation of anchoring force of the landslide with straight－line surfaces

为了避免出现群锚效应，工程中同一工点的锚固单体往往采用同一锚固角θ以及规则的间距进行布置。由于直线形滑面的倾角β固定，各锚固单体的锚固力在平行于滑面和垂直于滑面上的分解系数完全相同，故可用一处锚固单体代替锚固体系进行受力计算，如上图1示。可以计算得出滑体下滑推力T为：

而滑体与锚固结构作用于滑面上的垂向压力为：

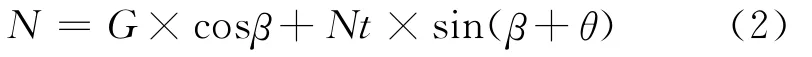
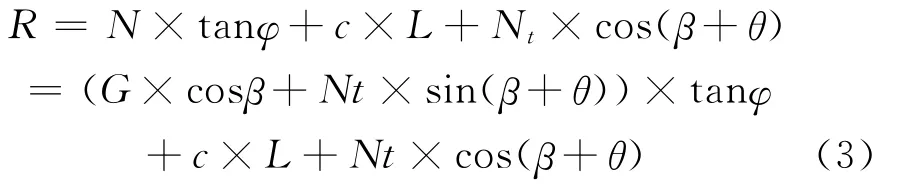
施加锚固力后，要求滑坡体的稳定性系数达到安全系数Ks。故有：

将式（1）、式（3）代入式（4），可得稳定性系数等于安全系数这一临界状态下的锚固力Nt为：

上述Nt为每延米滑体稳定性系数为Ks时，所需锚固系统提供的锚固力。根据滑坡横向上锚固单体的间距B，以及地层、锚固材料等资料所确定的锚固单体极限抗拔力Pa（也可采用现场抗拔试验获得），即可计算得出在坡面锚固范围1内所需布置的锚固单体根数n：

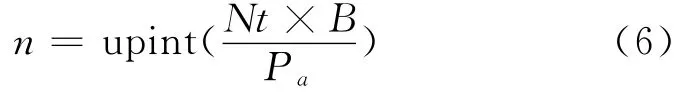
上式中的upint函数代表向上取整，例如：当自变量值为3.1根时，取4根。

在完成n值的计算后，根据Nt／n，即可计算得实际布置时每处锚固单体的设计锚固力。

以上计算流程建立在一个假定上，即整个锚固体系均布置在锚固范围1内；一旦锚固体系中有一个锚固单体进入锚固范围2时，虽然其锚固角仍为θ，但与该锚固单体相交的滑面倾角值已非直线形滑面倾角β，锚固单体与滑面之间的夹角发生了变化，导致锚固力的分解无定式。即，锚固力的确定依赖于锚固角θ与滑面倾角β的关系。

[2]许全兴：《〈实践论〉和〈矛盾论〉对马克思主义哲学中国化的启示》，《中国社会科学》2013年第12期。

3 基于概率理论的折线形滑坡锚固力计算方法

从前面对直线形滑坡的受力分析计算过程可见，该法无法直接运用于滑面倾角无固定值的折线形滑坡。对于这类滑坡中的锚固结构受力分析，工程中往往采用试算的方法，逐渐调整锚固范围内锚固单体的布置位置，利用与单体相交的某段滑面代表整个滑面，复核其稳定性直至达到略大于安全系数这一要求。这一方法具有随意性，将造成计算工作量的大量增加。此外，在进行锚固设计时，锚固范围内的所有滑面都可能与锚固单体相交，当单体大部分落于其中的某一滑面时，用该滑面的倾角代替整个滑面的倾角是合适的。然而一旦出现滑面变化较大、长度大致相等的情况，这一方法的适用性将大大地降低。

3.1 折线形滑坡锚固系统的期望角

从概率学的角度来看，当设计人员于锚固范围内的坡面上随机地布置一道锚固单体时，它必然会入射至锚固范围所对应的滑面区段上。对于工程上常见的折线形滑坡，由于滑面有限，倾角固定，当在锚固范围内随机布置锚固单体时，其入射至锚固范围内某个滑面这一事件可以视为随机事件，与锚固单体相交滑面的倾角值β则为离散型随机变量。该随机变量的所有可能取值为锚固范围所对应的各分段滑面的倾角值。对于这一随机变量，其数学期望代表了在坡面布置一道锚固单体时最有可能与之相交的滑面倾角值。该角度值可以最大程度地代表在一定的锚固范围内，锚固体系以θ角入射进滑面时与之相交的滑面倾角值，可称锚固范围一定且锚固角为θ时的滑面期望角，记作E（β）。对于滑面倾角为β的直线形滑坡，该随机变量取值为β时的概率为100%，即在锚固范围内任何部位布置一道锚固单体，它必然会入射至倾角值为β的滑面上，故期望角就为β；而对于折线形滑坡，其期望角数值则与坡面锚固范围、锚固角、滑面倾角及长度等因素有关，需进行概率分析才能获得。

折线形滑坡锚固系统期望角的提出，能够规避锚固力是作用于与锚固单体相交的滑面对应滑块还是作用于锚头对应滑块这一问题。其次，该角度值代表了滑面的综合倾角值，可利用该角度值按直线形滑坡进行折线形锚固力的计算。因此，当以该角度值配合试算法进行锚固系统的设计时，将大大地减小计算工作量。

3.2 期望角的计算方法

假定有一处锚固系统处治的折线形滑坡，锚固系统仍按等间距等锚固角进行布置，如图2所示。

图2 折线形滑坡的锚固系统计算简Fig.2 Calculation of anchoring force of the landslide with irregular－line surface

以该滑坡的坡面锚固范围顶部为起点，绘制一条与锚固入射线相垂直的辅助线，该辅助线止点位于从坡面锚固范围底点引出的锚固入射线交点上，如图2所示。由于这一辅助线与坡面锚固范围相对应，并与锚固入射线相垂直，故布置在坡面锚固范围的所有锚固单体必将全部入射到这一辅助线上，其上某一点处锚固单体的入射概率相比其它方向的直线都要大，且由于坡面锚固系统的等间距布置，锚固体入射到该辅助线上每一点的概率均相同，即该辅助线具有锚固单体全部入射、入射概率最大、概率分布函数为常数这三个特点。据这一特点，可将该辅助线称为锚固角为θ时锚固系统的最大概然入射线。

现将折线形滑坡各分段滑面向锚固系统最大概然入射线作投影，第i条滑面在最大概然入射线上的投影长Lti为：

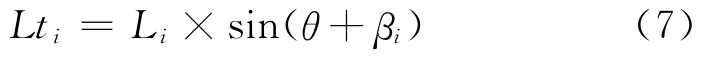
应注意，上式中的Li为锚固范围内第i段滑面的长度，它与锚固范围相对应，在首尾两处并不一定等于滑面长。

因锚固单体在最大概然入射线上某一点的入射概率为常数，故在坡面上布置一道锚固体，其入射到Lti这一范围上的概率pi为：

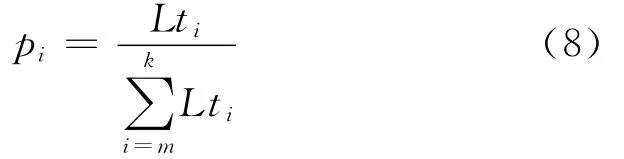
式中，m代表从上往下第一条在最大概然入射线上有投影的滑面编号，k代表从上往下最后一条在最大概然入射线上有投影的滑面编号。当锚固体以θ为锚固角时，它只能落在从上往下第m～第k条滑面间，其余滑面均不可能出现入射的情况；另，式（8）中分母代表的是最大概然入射线的长度。

由于Lti与Li之间为一一对应的关系，锚固单体入射到某一滑面Li上的概率也为pi。因此，锚固单体入射至某一倾角的滑面这一随机变量β的所有可能取值与该取值的概率如下表1所示。

表1 与锚固单体相交的滑面倾角概率分布表Table 1 Probability distribution of sliding surface's inclination－angle intersected with the anchoring bolt

故，一处锚固单体从边坡坡面锚固范围内，以θ角入射到折线形滑坡时，其期望角E（β）为：

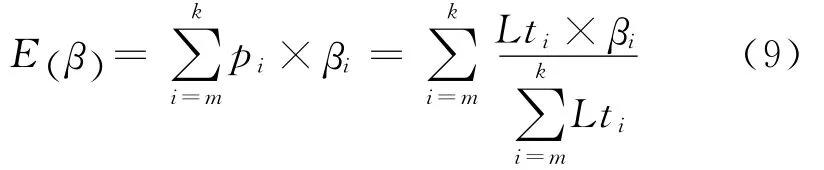
3.3 折线形滑坡的锚固结构设计流程

综合前面所述，基于概率论的折线形滑坡锚固系统设计流程如图3所示。从图中可以看出，本文所采用的方法与工程上常用的试算法相比，唯一的区别在于：本方法用考虑了锚固范围、锚固角、滑面倾角及长度等因素在内的期望角代替整个折线形滑面的倾角，而试算法则用某个滑面的倾角代替整个滑面的倾角。显然，前者不仅取值上更合理，而且可以避免试算法中，可能因反复调整参与计算的滑面倾角所造成的繁重工作量。

图3 锚固体的设计流程图Fig.3 Flow chart of anchoring design based on

经多个实例的计算验证（由于文章篇幅有限，下文将只列举一个实例进行验证），利用上述流程来代替折线形滑坡中的滑面倾角所确定的锚固力及锚固单体根数，能够在1～2次的计算循环下完成全部计算。

4 工程应用实例

某高速公路互通BK0＋030～BK0＋250段穿越斜坡地貌。地质调查表明，该处坡面岩体裸露，且发育有逆断层F1与路线斜交，上盘出露钙质泥岩、泥岩、泥灰岩，下盘为泥灰岩。受断层影响，岩体呈碎裂状，后期虽有一定程度的固结，但抗风化能力差。路线以路堑形式通过，设计坡高约46 m。施工图设计时采用框架锚杆配合绿化予以加固。

路堑边坡于2009年开挖成型，因坡面植被防护滞后，导致岩体反复受水浸泡软化，于2011年雨季期间出现数次垮塌。经多次采用锚杆、锚索等措施进行处理，效果仍不佳。2011年11月，＋090～＋115段边坡在雨后再次出现了滑塌，坡面出现了3～5 m深的凹槽，滑塌体风化程度极高，大部分手可捏碎。

经现场调查及论证后，最终的方案为采用混凝土嵌补配合框架梁锚索的方式对其进行处治。根据勘察资料及锚索成孔资料，获得了边坡深部潜在的折线形滑面。经计算，利用嵌补体恢复至原设计坡比后，其下滑推力将达1 665 k N／m。采用15°的锚固角进行锚索系统的设计。

采用本文推荐方法，计算得到潜在滑面的期望角为46°，设计锚固力为1 581.5 k N／m。按3 m纵向间距布置预应力锚索系统，根据地层情况及拟采用的锚索型号，确定单根锚索锚固力为650 k N，计算所需锚索根数为7.3根，实际需布置8根。在断面上可按4 m间距布置（顶部两道4φs15.2 mm锚索在滑塌前已施作，在滑塌过程中有扰动，无法作为工程永久处治措施），单根锚索的设计锚固力为593 k N／道，典型断面布置图如图4所示。按该设计锚固力核算得边坡稳定性系数为1.28，略大于边坡安全系数1.25，无需调整锚固角。经锚固段结构计算，需采用6φs15.2 mm锚索，其锚固段长度为10 m，锚固体直径为130 mm。

若采用目前工程上常用的试算法计算锚固力，由于该滑坡坡面锚固范围所对应的滑面（如虚线所示）共有四段，从上往下倾角值分别为59°、50°、39°及23°，这些滑面倾角值即为试算法中的所有β可能取值。经试算，最好的情况是，所有设计的锚索正好入射进位于50°的滑面上（据概率分析结果，这一事件概率仅为37.4%），而这一倾角正好也最接近期望角46°。为了与采用期望角的计算方法相比，仍按3 m纵向间距布置，计算锚索根数仍为8根，单根锚索分配的实际设计锚固力则为617 k N／束，大于采用期望角计算得到的实际设计锚固力，造成预应力的浪费。因此，对比这两种方法可以发现，利用期望角计算折线形滑坡的锚固力及锚固布置情况，可减少计算工作量并获得较优结果。

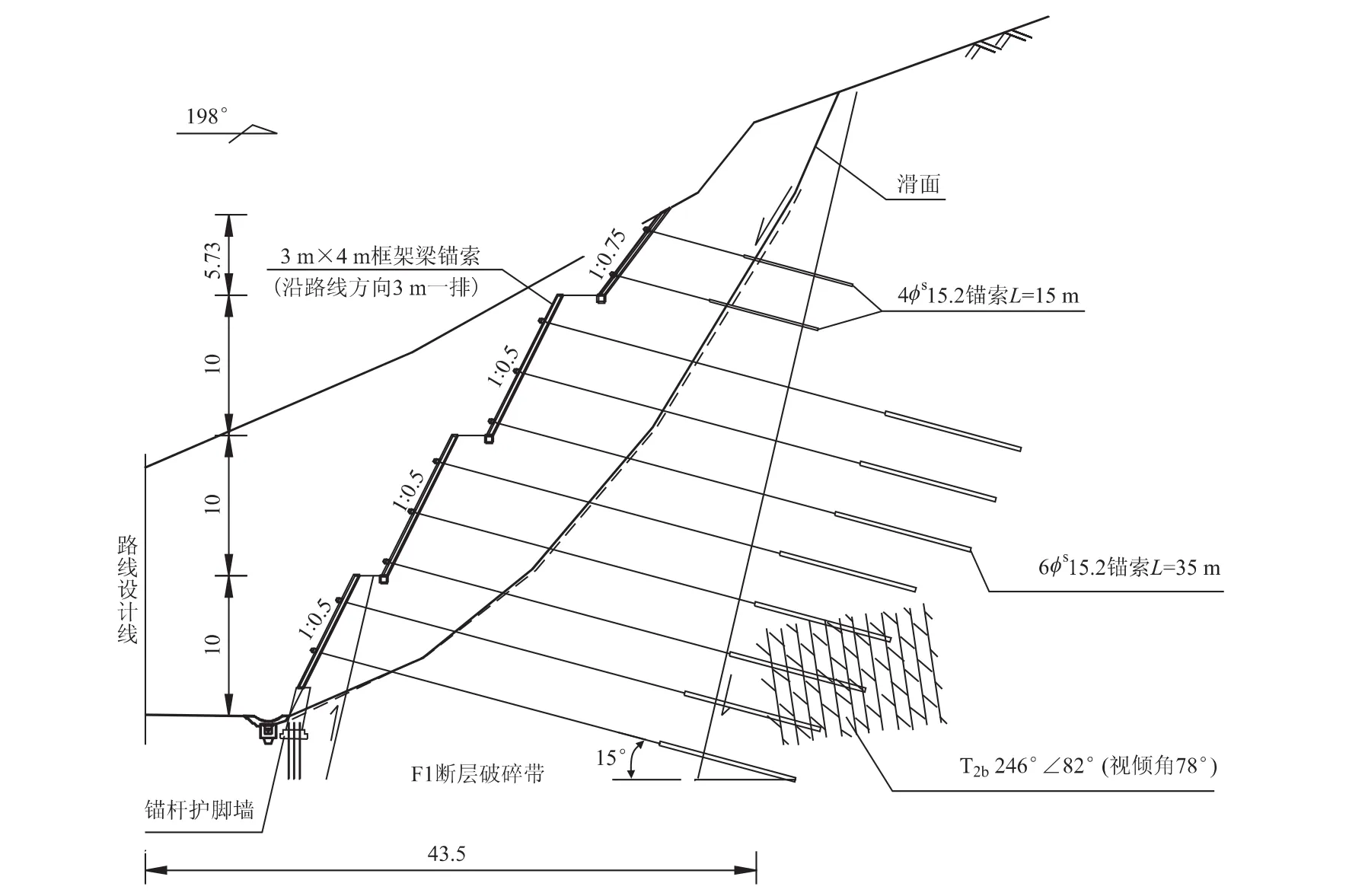
图4 边坡处治设计典型横断面图Fig.4 Typical cross－sectional view of slope treatment

该工点已于2012年2～3月完成施工，在经历了2012年、2013年两个雨季后，该处边坡稳定状态较好，无变形、滑塌等迹象，表明应用以上方法计算得出的锚索加固系统取得了良好的加固效果。

5 结论

在应用锚索或锚杆对折线形滑坡进行加固时，由于滑面不规则，使得锚固力的计算及最后确定锚固体的分布形式和数量这一系列工作，都比直线形滑坡复杂得多。与工程上常采用的试算法相比较，针对参与锚固结构受力计算的滑面倾角取值这一步骤，本文从锚固单体入射进某一折线形滑坡各滑面存在一定概率这一观点出发，引入了折线形滑坡锚固结构的最大概然入射线和期望角两个概念，用考虑了锚固范围、锚固角、滑面倾角及长度等因素在内的期望角代替整个折线形滑面的倾角，最终将折线形滑坡锚固受力计算转变为直线形滑坡锚固结构受力计算，大大地简化了折线形滑坡的锚固结构受力计算的流程。工程应用实例证明，该方法不仅可以减少锚固系统的设计工作量，而且可以降低锚固体材料的浪费。

［1]李海光，等.新型支挡结构设计与工程实例（第二版）［M].北京：人民交通出版社，2004：319.

［2]蒋忠信.预应力锚索加固松散体滑坡的机理与实例［J].铁道工程学报，1999，（1）：72－77.

［3]梁瑶，周德培，赵刚.预应力锚索框架梁支护结构的设计［J].岩石力学与工程学报，2006，25（2）：318－322.

［4]任红卓，郭文静.边坡地梁锚索加固中的锚固角设计［J].水利与建筑工程学报，2010，8（2）：159－161.

［5]李建国.预锚格构体系中不同锚固角的仿真分析［J].西部探矿工程，2008，20（8）：39－42.

［6]杨雪莲，周永江，等.框架预应力锚索在滑坡加固中的现场试验研究［J].西南公路，2011，（2）：75－78.

［7]郑颖人，陈祖煜，等.边坡与滑坡工程治理（第二版）［M].北京：人民交通出版社，2012：481－483.

［8]重庆市建设委员会.建筑边坡工程技术规范（GB50330－2002）［S].北京：中国建筑工业出版社，2002.

［9]刘才华，陈从新，冯夏庭.土质边坡预应力锚索设计方法探讨［J].岩土力学，2006，27（8）：1349－1352.

［10]蒋楚生，周德培.非圆弧形滑面中满足平衡条件的预应力锚索设计拉力的确定方法［J].铁道学报，2006，28（5）：125－128.