三维数值模拟在地下工程围岩二次应力－形变场研究中的应用

张莹，朱俊秋，张红

（1.中铁二院工程集团有限责任公司，成都 610031；2.中国轻工业成都设计工程有限公司，成都 610000；3.中国地质调查局成都地质调查中心，成都 610081）

1 引言

地下工程在开挖之前处于初始应力平衡状态，开挖后由于临空面的出现，给了岩体变形和位移的空间，从而导致围岩的变形甚至破坏，以及变形破坏过程中围岩应力的重分布，即二次应力－形变场的形成。围岩的二次应力状态较之初始应力状态有了很大的调整，是分析开挖后围岩稳定性的关键，但由于其复杂性，因此难于准确把握［7]。

本文以西南地区在建的某水电站地下洞室群为例，介绍三维数值模拟方法在这一问题研究中的操作过程及取得的成果，可以为类似问题的研究提供一定参考。

2 三维数值模拟方法介绍

研究地下工程开挖问题常用的数值模拟方法有有限元法、有限差分法、快速应力边界法、离散元法、DDA法等。相对于其他几种方法而言，有限元法和有限差分法及快速应力边界法（S－B法）是目前公认的三种解决地下工程问题的最有效、通用的方法。本次研究采用快速应力边界法及有限差分法这两种方法。

快速应力边界法（S－B法）［8]：该方法由李仲奎、戴荣等人提出，经过工程实践证明，该方法对深埋地下工程初始应力场的拟合具有较好的效果。其基本思路为：在初始地应力场的生成过程中，数值模型不设置速度边界条件，只是在模型的边界上根据应力场的分布情况施加恒定的应力边界条件。这一应力边界条件作为模型最外层单元的受力条件转化成节点力作用在模型最外层单元的节点上，由于边界条件保持恒定，即最外层单元边界上的节点力标尺不变，因此就相当于给模型添加了构造应力边界条件，然后通过迭代计算，表面的应力分布逐渐向模型内部扩散，直至达到平衡。这时生成的初始应力场可以认为是构造应力场和自重应力场的叠加场。

有限差分法［9]：属于连续介质数值分析方法。其特点是直接求解基本方程和相应定解条件的近似解。一个问题的有限差分法求解步骤是：把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地用代数方程组来代替，即有限差分方程组，求解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。利用有限差分法来模拟围岩的二次应力－形变场可以取得较好的效果。

3 数值模拟过程

初始应力场是地下工程开挖后发生变形和破坏的根本作用力［10]，直接影响围岩二次应力－形变场。因此要想获得较为准确的围岩二次应力－形变场，除开根据实际的开挖情况及支护情况进行开挖及支护的模拟外，首先要模拟出较为准确的初始应力场。

3.1 初始应力场模拟过程及成果

对于深埋地下工程，目前较常用的初始应力场模拟方法为快速应力边界法，其模拟及求解步骤为：

（1）选择和建立三维数值计算模型。包括计算域的选择和计算坐标系及计算网格的划分。

（2）岩体特征及主要结构面的模拟。模拟时应考虑不同的地层岩性、不同的围岩类别、控制性结构面，并根据所选择的计算模型对该模型所涉及到的岩体及结构面参数依据同类工程经验进行取值。

（3）施加模型的边界及约束条件。快速应力边界法的原理及思路是计算过程中模型不设置任何约束条件，仅在模型表面根据地应力的实际分布情况施加应力边界。因此选择快速应力边界法来模拟初始应力场时，只需设置应力边界。

（4）进行数值计算，并根据计算结果不断的调整应力边界，直到计算应力场与实测应力场在应力量值和应力方位都达到最大的拟合为止。

本次研究进行模拟时，采用的模型是摩尔－库伦模型（Mohr－Coulomb Model），前期的建模及网格划分工作在ANSYS有限元程序中进行，然后导入FLAC3D有限差分程序中进行初始应力场求解。本次初始应力场拟合在应力量值（图1）和应力方位（图2）两方面都取得了较好的效果。

由图可见虽然局部测点处某一个或两个主应力拟合效果不是很理想，但从平均相对误差的角度来看，由于其可以从一定程度上反映出应力场总体的特征，因此可以认为计算应力场和实测应力场的量值在总体上拟合效果还是较理想的，其中最大、最小主应力的拟合效果最佳，中间主应力次之。

由上图可知，所获得的初始应力方位与实际情况也非常吻合。为后续地下洞室群开挖围岩稳定性分析提供了较好的初始条件。通过上述拟合获得了初始应力场的分布特征（图3）。

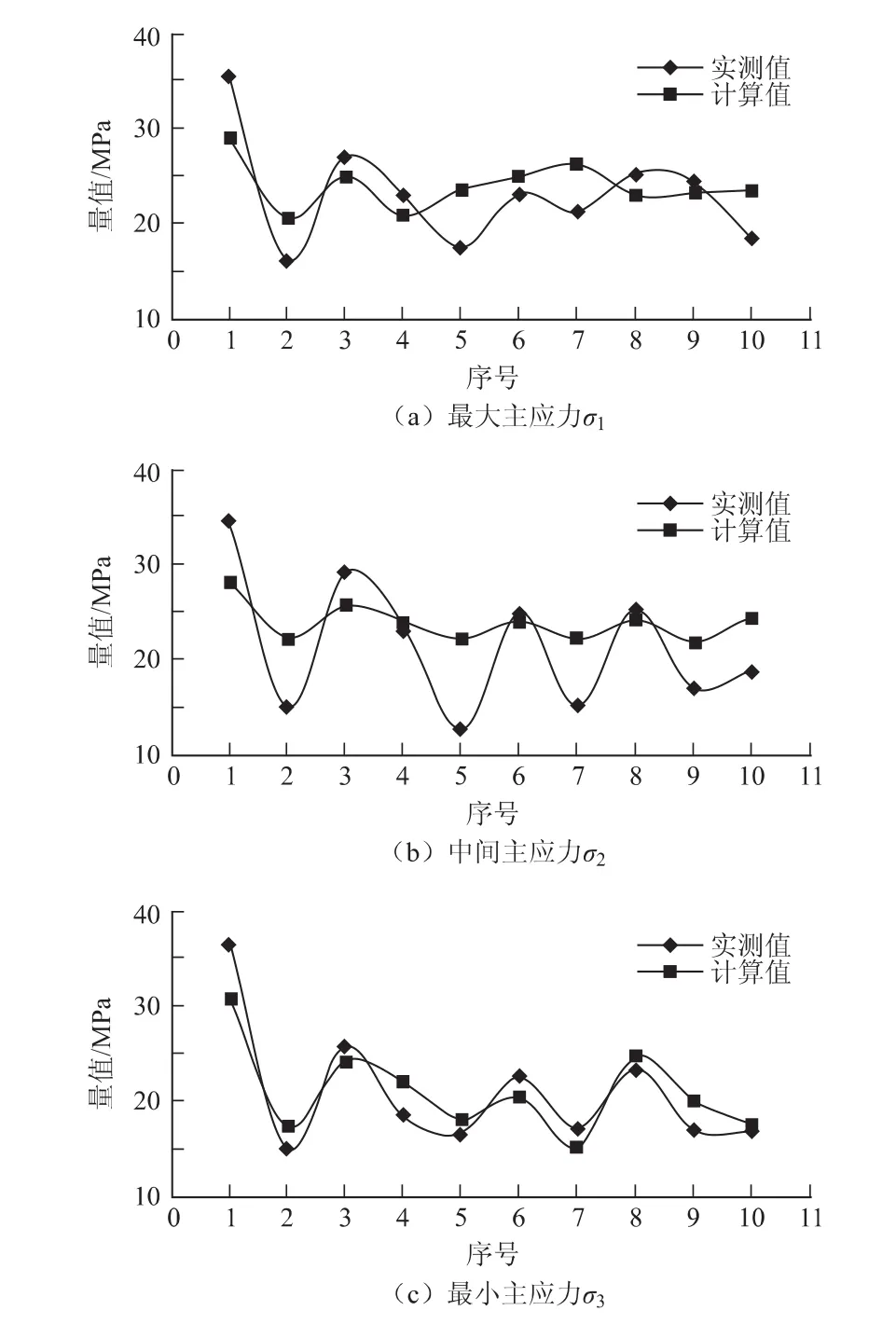
图1 初始地应力量值拟合效果图Fig.1 Fitting effect of initial geo－stress values

从该图中可以获得初始应力场的量值范围及各主应力随空间的变化规律，以及应力集中的部位等有用的数据。

3.2 围岩二次应力－形变场模拟过程及成果

了解二次应力场的分布规律，对分析围岩变形破坏成因机理具有重要意义。在前述所获得的初始应力场的基础上，按照施工中所采用的开挖顺序，模拟开挖，并及时支护，获得开挖支护情况下的围岩二次应力场和位移场。

模拟及求解的过程可按以下步骤进行。

（1）初始应力场求解。

（2）模型节点位移全部清零，施加速度边界条件。

（3）采用空单元模拟开挖。

（4）编写支护措施的命令流文件，通过“call”命令导入程序中，完成支护的模拟。

（5）求解，直至收敛。

（6）查看结果。

以上步骤均在FLAC3 D程序中进行，开挖的顺序可在建立计算模型时在ANSYS程序中利用“工作平面”功能对地下工程进行剖分（图4），形成各开挖层，在FLAC3D中进入到上述步骤（3）时再一层一层开挖，这样可以达到按实际开挖顺序及情况进行开挖的效果。此外，在进行上述步骤（4）时，应尽可能的和现场实际的支护情况（如：支护形式、支护部位、各支护措施采用的参数等）想吻合，以求获得最近真实的二次应力－形变场。

通过上述过程可获得地下工程开挖至各个阶段的围岩二次应力－形变场，然后利用Tecplot程序从FLAC3D中调取，如图5、图6。

图5和图6仅为某一断面的形变信息及应力信息，完成上述模拟过程之后还可以调取地下工程各个部位的应力及形变信息，即获得了整个地下工程的二次应力－形变场，这些信息的获得有助于分析围岩的变形破坏问题。

4 结语

地下工程开挖后的围岩变形破坏问题是直接影响地下工程建设的关键问题，正确认识开挖后的围岩二次应力－形变场对解决这一问题有至关重要的作用，通过三维数值模拟来获得围岩的二次应力－形变场可以起到很好的效果。

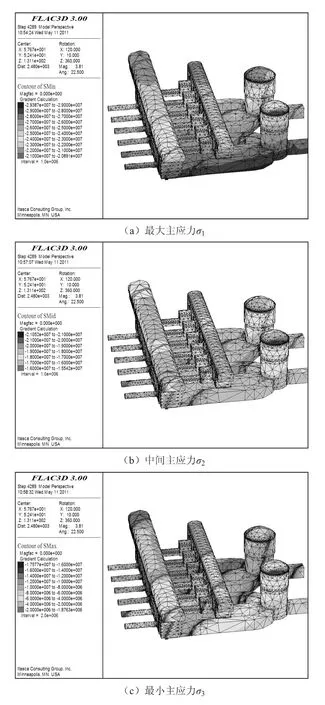
图3 地下洞室群岩体初始地应力分布规律Fig.3 Distribution r ule of rock initial geo－stress

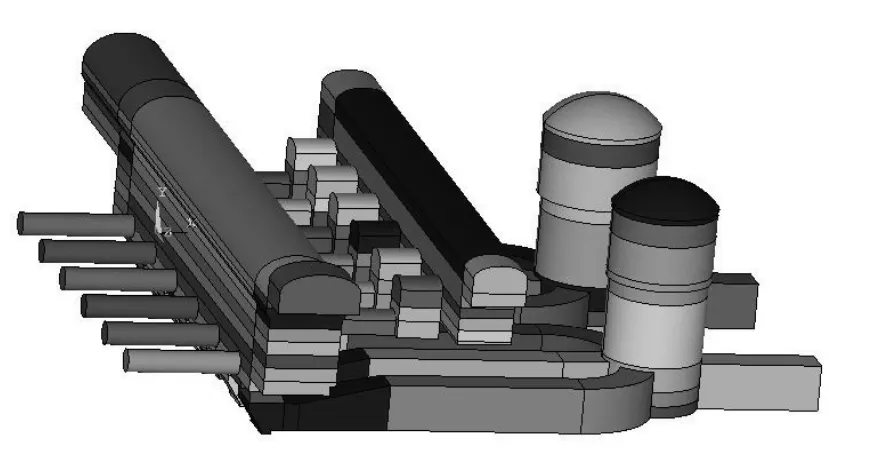
图4 洞室群分层开挖有限元模型Fig.4 Finite element model of the stratified excavation

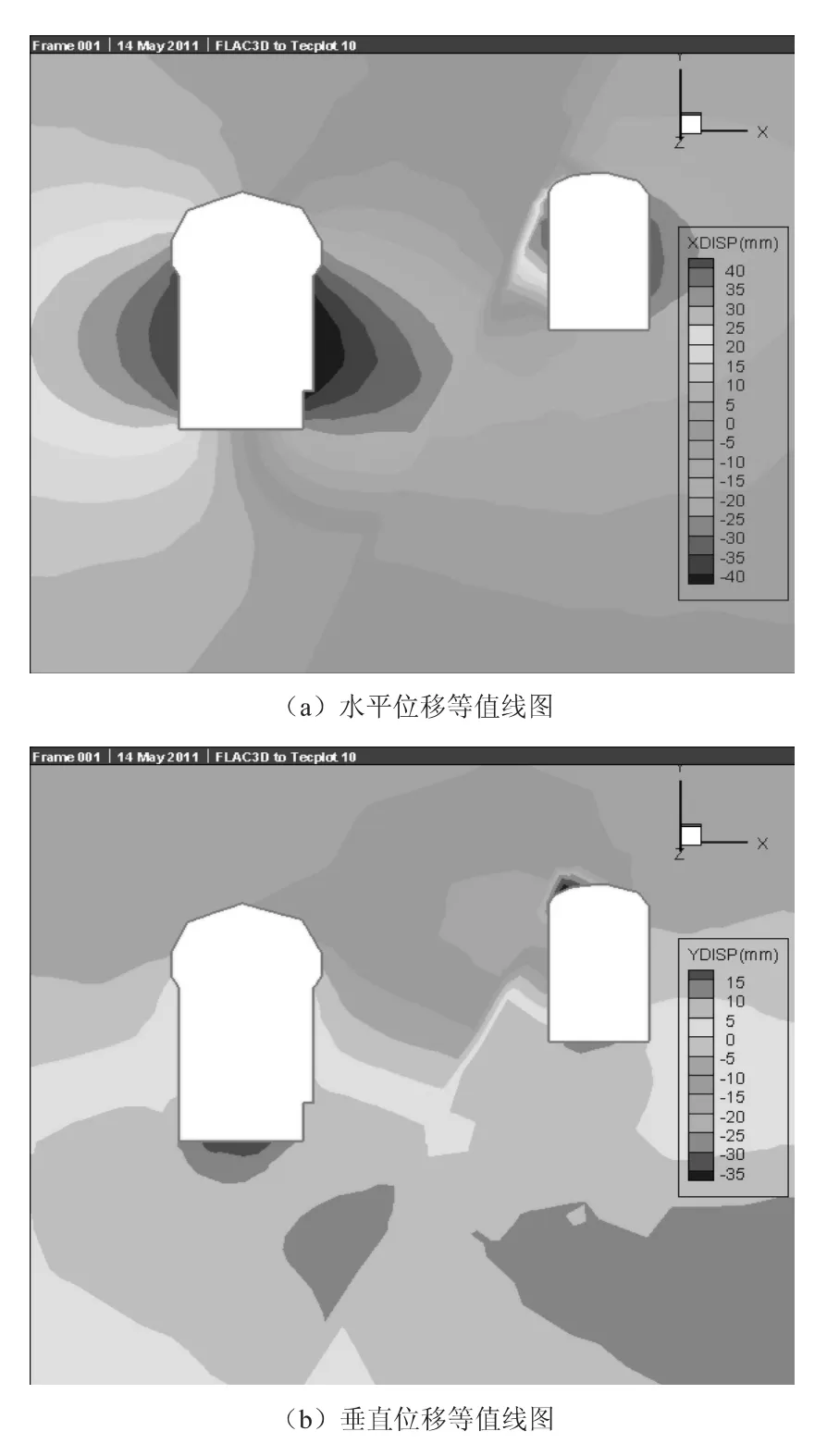
图5 开挖结束后某断面位移等值线图Fig.5 Contour map for the displacement of a section

本研究介绍了三维数值模拟方法在研究围岩二次应力－形变场中的模拟过程及取得的成果，可以为这一问题及同类似问题的研究提供一定参考，具有一定指导意义。

［1]王思敬，等.地下工程岩体稳定分析［M].北京：科学出版社，1984.

［2]李华晔.地下洞室围岩稳定性分析［M].北京：中国水利水电出版社，1999.

［3]张倬元，王士天，王兰生，等.工程地质分析原理［M].北京：地质出版社，2008.

［4]李仲奎，周钟，汤学峰，等.锦屏一级水电站地下厂房洞室群稳定性分析与思考［J].岩石力学与工程学报，2009，28（11）：2167－2175.

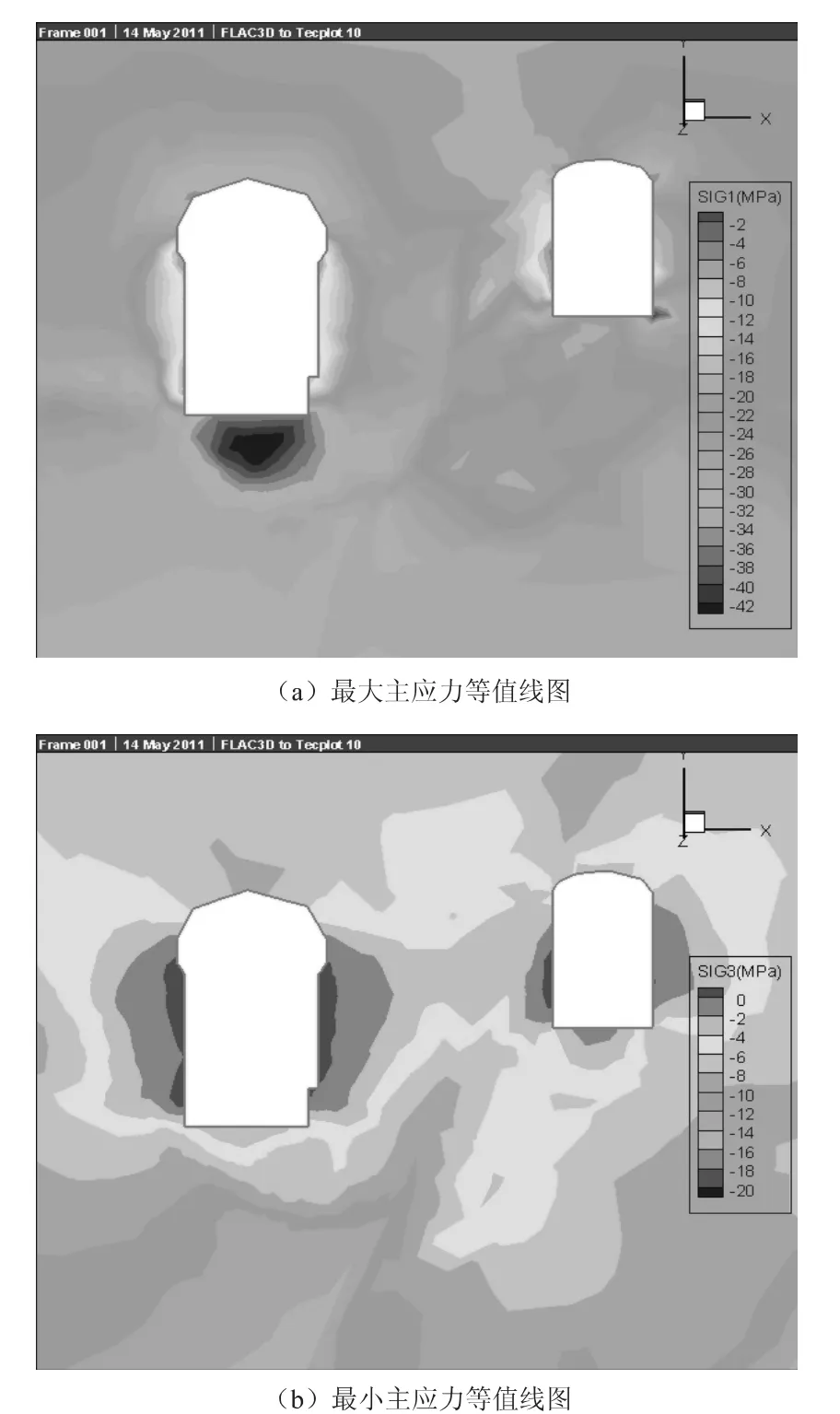
图6 开挖结束后某断面主应力等值线图Fig.6 Contour map for principal geo－stress at a section after excavation

［5]黄润秋，黄达，段绍辉，等.锦屏Ⅰ级水电站地下厂房施工期围岩变形开裂特征及地质力学机制研究［J].岩石力学与工程学报，2011，30（1）：23－35.

［6]杨述仁，周文铎.地下水电站厂房设计［M].北京：水利电力出版社，1993.

［7]张莹.锦屏一级水电站地下厂房围岩变形破坏特征及地质力学机制研究［成都理工大学硕士论文]［D].成都：成都理工大学，2011.5.

［8]陈育民，徐鼎平.FLAC／FLAC3D基础与工程实例［M].北京：中国水利水电出版社，2009.1.

［9]M S Diederichs，P K Kaiser.Tensile strength and abut ment relaxation as fail urecontrol mechanisms in under ground excavations［J].Inter national Journal of Rock Mechanics and Mining sciences，1999，12（36）：69－96.

［10]杨林德，等.岩土工程问题的反演理论与工程实践［M].北京：科学出版社，1995.4.