四足机器人砂砾地面对角行走控制方法

程 品，罗 欣，顾瀚戈

（华中科技大学数字制造装备与技术国家重点实验室，湖北 武汉 430074）

四足机器人砂砾地面对角行走控制方法

程 品，罗 欣，顾瀚戈

（华中科技大学数字制造装备与技术国家重点实验室，湖北 武汉 430074）

为解决四足机器人在砂砾地面上对角行走容易失稳的问题，提高机器人对松软和凹凸不平地面的适应性，在位置控制的基础上提出了一种机身姿态角的调整策略，并在机器人对角行走的过程中采取了一种变阻抗参数的阻抗控制方法。最后在实际的砂砾地面进行了四足机器人对角行走实验，实验结果证明这种控制方法和调整策略对于四足机器人对角行走在砂砾地面上具有较好的控制效果。

四足机器人；对角行走；阻抗控制；砂砾地面

四足动物的对角行走步态是指对角腿同相运动的行进模式，即每次一组对角腿处于着地状态，另外一组对角腿处于摆动状态，两组交替运动，实现身体的行进。相对于每次抬起一条单腿的行走步态来说，对角行走步态的行进速度更快，是四足动物实现快速行走的基本步态，也是四足机器人实现快速运动的期望形式。但是由于在对角步态行进时，机器人的机体总是处于动态平衡状态，因此，同一组处于摆动相的腿在着地时必须保证同时“踩实”，才能进行另一组对角腿的切换，否则将会引起机身姿态角发生大幅度变化，从而造成机器人失稳。传统的步态控制方法主要是位置控制，即控制腿的末端按照既定的轨迹规划运动，但是并不能保证腿的末端“踩实”，尤其是在地面刚度低，地形凹凸不平的砂砾地面上进行对角行走时，情况更甚，因此要实现四足机器人在砂砾地面上的稳定行进，必须考虑机器人与外界环境交互的作用力，采用阻抗控制是解决这一问题的必由选择。

阻抗控制是通过控制力和位置之间的动态关系来实现柔顺功能，这样的动态关系类似于电路中的阻抗概念，因此而得名。阻抗控制把力偏差信号加至位置伺服环，以实现力和位置的混合控制，这样很好解决了单纯位置控制方法未考虑与外界环境作用力的问题。

阻抗控制作为机器人柔顺控制的一种基本方法，在工业机器人领域已得到较为广泛的研究与应用。Hogan在1985年提出利用Norton等效网络概念，把外部环境等效为导纳，而将机器人等效为阻抗，这样有效地将机器人的位置与末端作用力联系在一起[1～2]。Ikeura则提出变阻抗参数控制方法，通过选择最优的环境交互参数调整机器人的阻抗参数来满足不同任务的需求[3]。Buchli提出一种增强学习的算法来实现变阻抗控制[4]，阻抗控制目前也逐渐应用在双足机器人[5]、四足机器人[6～7]、六足机器人[8]身上，具有较好的控制效果。

本文在机器人腿末端位置控制的基础上，采用变阻抗参数的阻抗控制方法，能够有效调整四足机器人机身姿态角，实现了四足机器人在砂砾路面上稳定的对角行走，大大提高了机器人对砂砾路面的适应性。

1 四足机器人对角行走的位置控制

1.1 单腿的末端轨迹规划与位置控制

四足机器人在对角行走过程中，每条腿在着地相和摆动相之间来回进行切换。着地相是指单腿足端开始着地到再次抬腿离地期间腿的连续相位变化过程，摆动相则是从抬腿时足端离地开始到迈腿后落地期间腿的相位变化过程。

单腿的末端轨迹规划主要是针对摆动相而进行设计的，处于摆动相的腿的运动可以看成是由水平方向（X方向）和竖直方向（Z方向）运动合成而来。为保证运动的连续性和足端运动起止时刻的速度、加速度为0，X方向和Z方向都需要满足位移连续、速度连续和加速度连续等6个约束条件，X方向和Z方向的位移均为五次曲线时才可以满足规划需求。设定最大抬腿高度为H0，迈腿距离为S0，运动周期为Ts。

于是有：

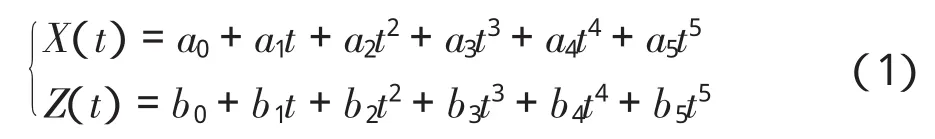
本文只针对基本行走步态的轨迹规划，这样X方向和Z方向的约束条件分别为：

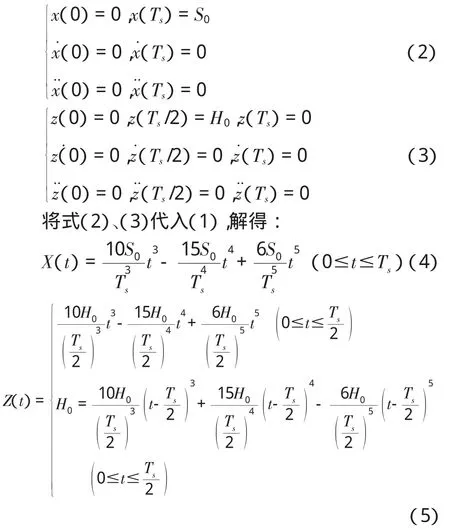
当单腿运动规划好末端轨迹后，通过逆运动学模型可以求解出当前各个驱动器应该达到的位移量，结合传感器测量出的当前实际运动位移，通过增量式PID控制算法来进行伺服控制，算法框图如图1所示。

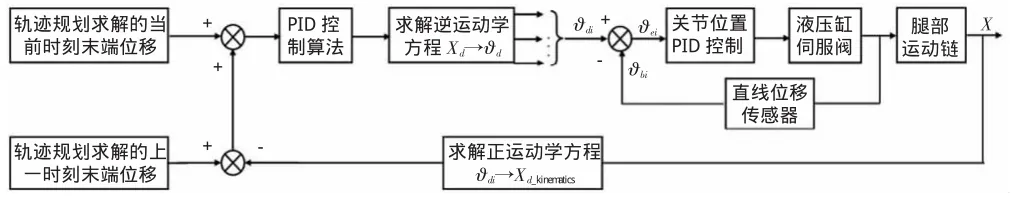
图1 位置控制算法框图

1.2 对角行走中的姿态控制

四足机器人在对角行走过程中，其机身姿态角，包括偏航角 αy、俯仰角 αp、横滚角 αr，进行实时控制，使其保持在一定范围内。机身姿态角的调节是通过机器人处于着地相的腿来进行调节的。

如图2所示，若机器人在对角行走的过程中偏航角αy出现偏差，则处于着地相的两条腿相对于机身坐标系向外侧移来产生一个与αy角相反的力矩来调整这一偏差。在本文中，每一个步态周期对偏航角进行一次纠正。

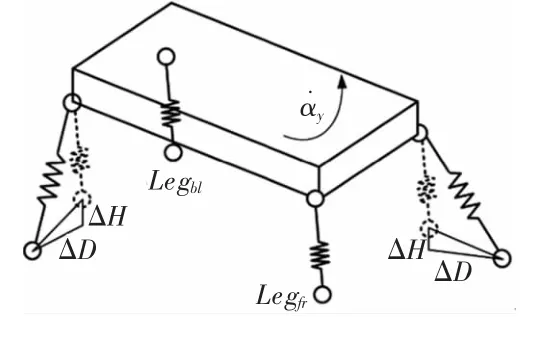
图2 偏航角调整示意图

偏航角的位置补偿量通过PD控制器计算给出，即

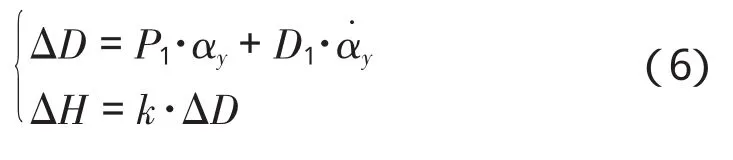
其中，

αy为偏航角；

α觶y为角速率；

P1、D1为控制器比例和微分系数；

△D、△H为姿态补偿量。

四足机器人在对角行走过程中，横滚角αr控制不当极有可能导致机器人倾翻，而横滚角的控制依然是由处于着地相的这组对角腿来进行调整的，如图3所示。

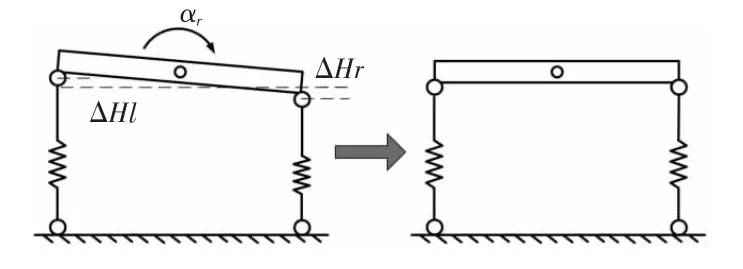
图3 横滚角调整示意图

横滚角的位置补偿量通过PD控制器计算给出:

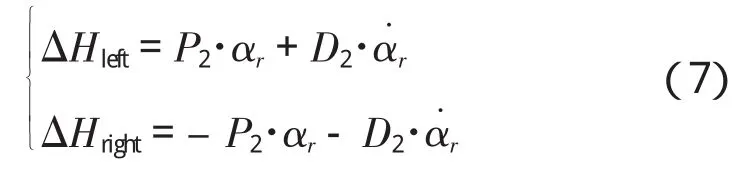
其中，

αr为横滚角；

α觶r为角速率；

P2、D2为控制器比例和微分系数；

△Hleft、△Hright为姿态补偿量。

与偏航角控制不同，横滚角的控制在机器人的一个步态周期内是实时控制的，每次的补偿量叠加到相应的着地腿的期望轨迹中，从而实现机身姿态横滚角的实时稳定控制。

2 四足机器人对角行走的阻抗控制

2.1 基于位置的阻抗控制

如图4所示为四足机器人等效阻抗模型图，可以将机器人每条腿等效成质量、阻尼和弹簧，这样每条腿可以看做是一个简化的线性二阶系统。

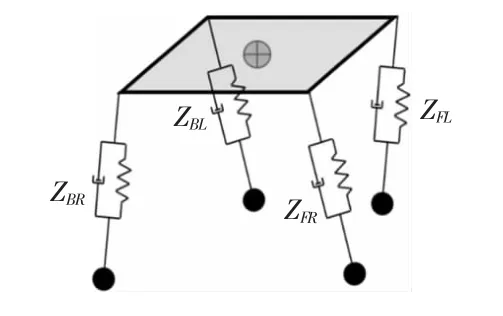
图4 等效阻抗模型

由于对角行走过程中机器人腿部所受外界环境的作用力主要是竖直方向，本文只考虑竖直方向的阻抗控制，将传感器的竖直方向的力fz作为阻抗控制器的输入。阻抗控制器可以用以下方程来进行表达：

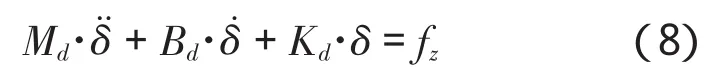
其中，

Md为质量矩阵参数；

Bd为阻尼矩阵参数；

Kd为刚度矩阵参数；

δ为阻抗控制器输出参数-位置补偿量；

δ觶 为速度项；

δ咬 为加速度项。

如图5所示为基于位置的阻抗控制算法框架图，算法由位置控制内环和阻抗控制外环组成，阻抗控制器输出的位置补偿量叠加到期望的末端轨迹上，输入到内环的位置控制器，从而实现机器人由目标阻抗参数确定的目标动力学特性。

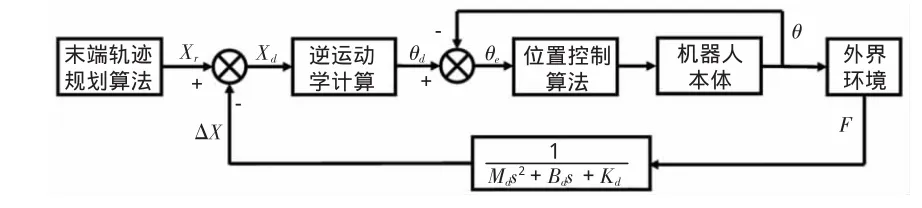
图5 基于位置的阻抗控制框图

2.2 变阻抗参数控制方法

当四足机器人对角步态行进在不平路面中时，考虑到地面的复杂多变性，可以将着地相和摆动相进一步细化为几种不同的有限状态，如图6所示为一组对角腿在对角行走一个周期内4种状态切换图。

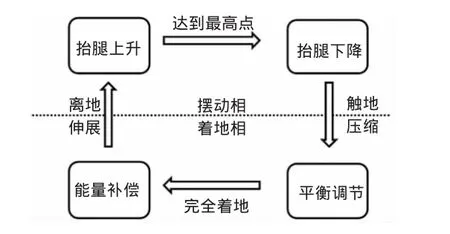
图6 腿部运动状态切换图

机器人一组对角腿处于摆动相时，与外界环境没有作用力，其控制方式为位置控制，末端跟踪预先规划的轨迹，与此同时，另外一组对角腿则处于着地相，其控制方式主要为基于位置的阻抗控制。平衡调节状态主要是通过控制方法使刚触地的腿调整对应的阻抗参数和位置来保证机身姿态角的稳定，能量补偿状态主要是通过调整着地腿的刚度，补偿机器人腿部与环境相互作用所损失的能量。着地相的这两种状态对于控制机器人稳定对角行走具有非常重要的作用。

当机器人对角腿处于不同的状态下，考虑使用不同的阻抗参数，来实现整个运动过程中的柔顺性，由公式（8）得，

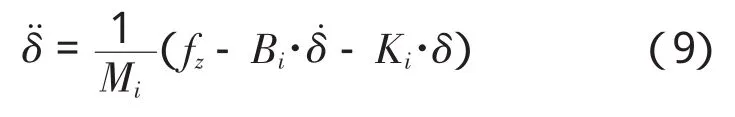
其中，Mi、Bi、Ki为机器人处于第 i个状态下的阻抗控制参数。

机器人在对角行走过程中，可以设定一组默认的阻抗参数[8]，当机器人处于其他状态时其阻抗参数刚度项都是在默认参数上添加一个系数与之相乘。默认的阻抗参数可以由下面的公式给出：

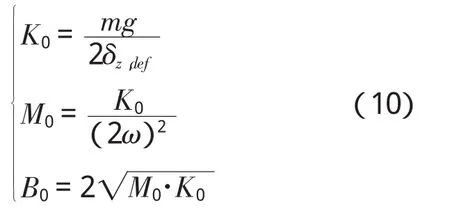
其中，δz，def为机器人在平地上稳定对角行走时，着地腿接触地面在Z方向的阻抗输出值，可以由实验进行确定，m为机器人的总质量，而腿的支撑相的频率为机器人对角行走频率ω的2倍，由此可以得到质量参数和刚度参数。阻尼参数被设置为临界阻尼比，减小二阶系统的超调量，阻尼比过小会造成腿部等效的二阶系统振荡，过大系统能量很容易被消耗掉[9]。

当机器人出现如图7所示情况，即其中一条腿提前着地而与其一对处于摆动相的腿还在空中，着地腿由于位置没到会继续下降，地面反作用力会对机身造成一定倾斜，这时必须改变着地腿的阻抗参数，否则机器人会失稳。

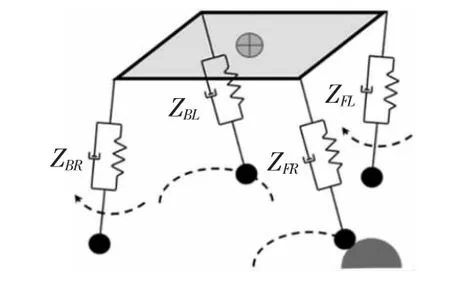
图7 凸起地形引起不同时着地

调整提前着地腿的阻抗参数如下：

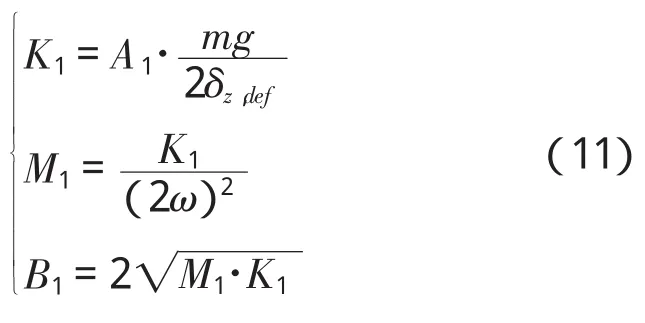
其中，A1小于1，减小提前着地腿的刚度和阻尼，保证机器人机身姿态不出现较大变化。

当机器人出现如图8所示情况，即其中一条腿已着地，位置控制已经到位，但由于地形凹陷的原因，另一条腿仍悬空，这时如果进行对角腿状态的切换的话，机器人腿由于未“踩实”，肯定会出现失稳现象。

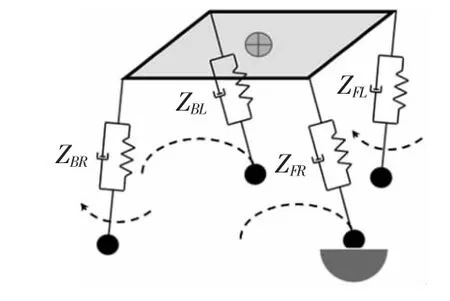
图8 凹陷地形引起不同时着地

机器人腿部由于仍处于悬空状态，腿部三维力传感器未检测到与地面作用力，这时机器人悬空腿应继续下降，同时调节其他三条着地腿的阻抗参数如下：

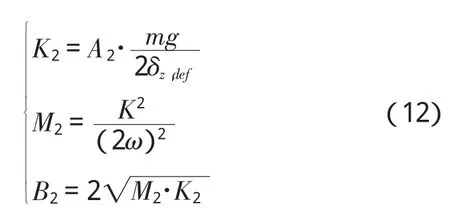
其中，A2小于1，减小腿部刚度和阻尼，机身高度相对于地面会下降，同时悬空腿下探通过力传感器检测到“踩实”后，即可进行对角腿的切换。

当对角腿处于着地相的平衡调节状态，主要进行调节机器人机身姿态角，使其保持一个稳定的范围内。前文提到的通过相应的位置补偿量，可以结合阻抗控制方法达到更好的效果，调整处于着地相的对角腿的刚度如下：

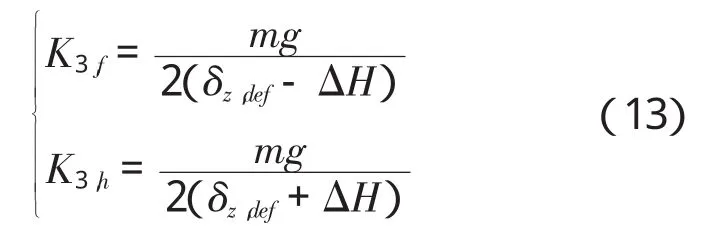
其中，△H为前文姿态控制中PD控制器计算得到的姿态补偿量。

当对角腿处于着地相的能量补偿阶段时，调整对角腿的刚度如下：

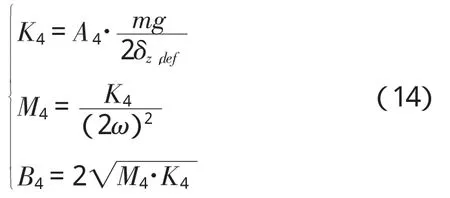
其中，A4大于1，增大腿的刚度是为了更好的储能，为机器人下一个对角行走周期补充损耗的能量。

3 四足机器人对角行走实验

3.1 实验平台MBBOT

如图9所示为液压驱动的四足机器人MBBOT的实物图。MBBOT主要由机体框架部分和四条相同的腿单元组成。机体框架部分搭载了全套的液压驱动和发动机动力系统设备，此外机体上还搭载了中央控制单元和惯性测量单元，机体连接四条腿组成完整的机器人实验平台。机器人前后腿结构相似，每条腿包括4个节段和4个主动自由度。4个主动自由度为横摆关节、髋关节、膝关节、踝关节，每个主动自由度均由一体化液压伺服驱动单元驱动。一体化液压伺服单元将液压缸和伺服阀集成在一起，并将一维力传感器和直线位移传感器集成在单元中，用于液压缸位置和力信息的反馈与控制。另外四条腿的足端也分别装有三维力传感器，用于检测腿与外界环境作用力的大小，作为阻抗控制器的控制输入。其整机性能及结构参数如表1所示。

图9 四足机器人MBBOT实物

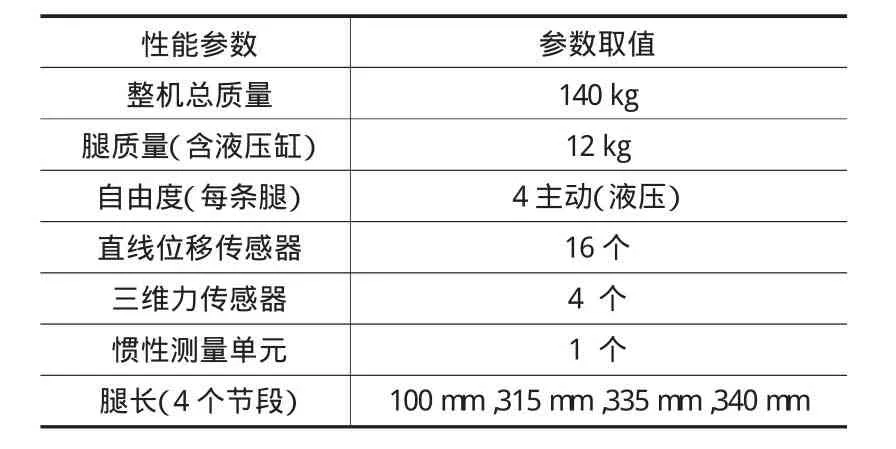
表1 四足机器人MBBOT性能及结构参数

3.2 室外砂砾地面实验

为了验证基于位置的变阻抗参数的阻抗控制方法在砂砾路面中的应用情况，将MBBOT放置在具有沙子和砾石的道路上进行对角行走实验。MBBOT从沙子地的一端硬土地上出发，依次经过沙子地和砾石地，到达砾石地的另一端硬土地上。当机器人行走在不同地形过渡阶段时，上位机给予机器人相应的指令，机器人进行相应的位置控制参数的调整；当进入同一地形时根据机器人所处的不同状态进行相应的阻抗参数调整。图10展示了MBBOT机器人对角行走实验场景，图11则显示了在实验过程中机器人机身姿态角的变化情况。

图10 对角行走实验场景图

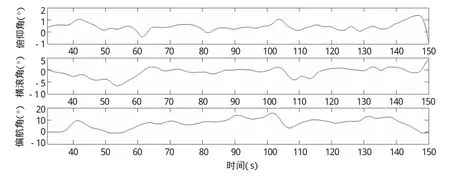
图11 机身姿态角变化曲线图

由图11可以看出，机器人行进53 s时，横滚角(roll)出现较大偏差，姿态角控制算法能够很好地抑制这种偏差，并恢复机身的稳定性。俯仰角(pith)在整个运动过程处于正常范围内波动，而偏航角(yaw)在运动过程中开始出现较大偏差，而最后通过变阻抗参数控制算法和姿态角调整策略，最终趋于稳定。

4 结束语

本文在位置控制的基础上提出了一种机器人机身姿态角调整策略，并针对四足机器人对角行走过程中不同状态采取变阻抗参数的阻抗控制，解决了机器人在砂砾这种松软以及凹凸不平地面上容易出现失稳的问题，通过实验证明了这种控制方法的有效性。

但是基于位置控制的算法对于机器人快速行走是有局限的，目前机器人用这种方法行走速度还是比较慢，未来工作应该考虑加上高速行走控制策略，比如基于弹簧倒立摆模型的足式机器人动平衡控制。目前机器人的控制只是考虑其运动学模型，未来工作应该加上其动力学模型，考虑关节的力矩控制以及关节力位混合控制等方法。

[1]Hogan N.Impedance control:An approach tomanipulation:Part I-Theory[J].Journal of Dynamic Systems,Measurement,and Control，1985，107(1):1-7.

[2]Hogan N.Impedance control:An approach tomanipulation:Part II-Implementation[J].Journal of Dynamic Systems,Measurement,and Control，1985，107(1):8-16.

[3]Ikeura,R.and H.Inooka.Variable impedance controlofa robot for cooperation with a human[C].Proceedings of IEEE International Conference on Robotics and Automation，Nagoya，May，1995（3）:3097-3102.

[4]Buchli J,Stulp F,Theodorou E,et al.Learning variable impedance control[J].The International JournalofRobotics Research，2011，30(7):820-833.

[5]Park JH.Impedance control for biped robot locomotion[J].IEEE Transactionson Roboticsand Automation，2001，17(6):870-882.

[6]Park J,Park JH.Impedance control ofquadruped robotand its impedance characteristicmodulation for trotting on irregular terrain[C].IEEE/RSJInternational Conference on IntelligentRobots and Systems(IROS)，Portugal，October，2012，175-180.

[7]FocchiM,Boaventura T,SeminiC,etal.Torque-control based compliantactuation ofa quadruped robot[C].12th IEEE InternationalWorkshop on Advanced Motion Control(AMC)，Sarajevo，March，2012，1-6.

[8]Huang Q.Softly stable walk using phased compliance control with virtual force formulti-legged walking robot[C].Proceedings of the IEEE International conference on Climbing and Walking Robots,Nagoya,September，2010，1-18.

[9]师汉民.机械振动系统—分析[M].武汉:华中科技大学出版社，2001.

ControlMethod ofQuadruped Robot Troton GravelGround

CHENGPin，LUOXin，GUHan-ge
(State Key Laboratory ofDigitalManufacturing Equipmentand Technology，Wuhan 430074，China)

Tomeet the demand ofquadruped robot trotting on the gravelground stability,improve the adaptability of the robot to the soft and uneven terrain.The adjustment strategy of attitude angles is proposed based on the position control,and take a variable impedance parameters of impedance controlmethod in the robot trotting process.Finally,the experiment of the robot trotting on the actual gravel ground is accomplished,experimental results show that this controlmethod and adjustmentstrategy for quadruped robot trotting on the gravelground hasgood controleffect.

quadruped robot；trot；impedance control；gravelground

TP242

A

1672-545X（2014）04-0008-05

2014-01-03

国家自然科学基金面上项目（编号：61175907）；高等学校博士学科点专项科研基金（编号：20130142110081）；国家自然科学基金创新研究群体科学基金（编号：51121002）资助。

程 品(1987—)，男，湖北黄冈人，华中科技大学在读硕士研究生，研究领域为机器人控制系统设计，机器人运动控制方法。