基于AHP-FIE的城市立交桥梁施工方法优化

2014-02-28黄海东

重庆交通大学学报(自然科学版) 2014年6期

黄海东，刘涛

(重庆交通大学土木建筑学院，重庆 400074)

随着国民经济的快速发展，工程技术的不断进步，近年来我国大中城市修建了许多快捷、方便、舒适的“城市绿色通道”——城市立交。由于其复杂性与特殊性，施工方法的优化选择面临一个重大的难题，仅凭经验和定性分析已不适应工程决策发展的需要，难以找到最优的方法。因此，应采用科学合理、系统全面的综合评价方法，作出定性分析与定量分析，以尽可能准确地选择最佳的桥梁施工方法。笔者运用了AHP-FIE综合评价体系对城市立交桥梁施工方法的综合评价进行阐述，解决了城市立交工程建设难题，降低施工风险，避免安全事故，使项目以“最低的损失，最大的效益”顺利完成。

1 AHP-FIE综合评价框架

层次分析法(Analytic Hierarchy Process，AHP)是美国运筹学家匹茨堡大学教授萨迪1970年应用于网络系统理论和多目标综合评价的方法，提出的一种层次权重决策分析方法[1]。模糊综合评判法(Fuzzy Integrated Evaluation)是一种以模糊数学为基础的综合评价方法。这种方法根据模糊数学中的隶属度理论，将定性分析转化为定量分析，对受到多种因素制约的事物做出一个总体的分析评价[2]。

AHP-FIE综合评价法是在层次分析法和模糊综合评判法基础上的一种扩展形式，其综合了以上两种方法的优点。首先，根据层次分析法的基本思想，将一个多目标的复杂决策问题作为一个系统，同时把目标分解为多个影响因素(指标)的阶梯层次，并且计算各个指标的权重值；然后，运用基于模糊数学中隶属度理论的模糊综合评价法，处理一些非确定性、模糊的问题，通过把定性分析转化为定量分析，清晰、直观地做出一个总体的评价。

1.1 AHP-FIE综合评价法的要素及流程图

评判的方案集T：T={方案T1，方案T2，…，方案Tm}={T1，T2，…，Tm}

评判的指标集U：U={指标U1，指标U2，…，指标Um}={U1，U2，…，Um}

指标的权重集W：W=w1，w2，…，wn

AHP-FIE综合评价法流程图见图1。

图1 AHP-FIE综合评价体系的流程Fig.1 Flowchart of AHP-FIE comprehensive evaluation system

1.2 计算指标的权重

利用层次分析法，并且引入“1-9标度法”[3](见表1)，通过问卷调查、专家评审等方式，确定各比较指标之间的相互重要性关系，得到判断矩阵A=(aij)n×n的相应元素的值，其中i，j=1，2，3，…，n(见表2)。

表1 1-9标度值及其含义Table 1 1-9 scaling value and meaning

表2 指标相对重要性的判断矩阵ATable 2 Index of relative importance of judgment matrix A

层次分析法采用重要性权值作为元素排序的评价指标，重要性权值是一种相对度量数，其值介于0～1之间，其数值越大，表示该元素越重要。笔者采用特征向量法中的方根法，计算判断矩阵A的特征值和特征向量，具体步骤如下。

1)计算判断矩阵A的每一行元素连乘积的n次方根mi

(1)

2)归一化向量

(2)

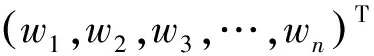
3)计算判断矩阵A的最大特征向值

(3)

4)一致性检验

为保证应用层次分析法得到的结论合理，需要对构造的判断矩阵进行—致性检验。其检验步骤如下。

①计算一致性指标

(4)

式中：CI值为度量判断矩阵偏离一致性的指标。当CI=0时，表明判断矩阵具有完全一致性；CI值越大，表明判断矩阵偏离完全一致性的程度越大；CI值越小，表明判断矩阵的一致性越好。

②计算一致性比例

(5)

式中：RI为平均随机一致性指标，查表3可得。

表3 平均随机一致性指标RI取值Table 3 Average random consistency index RI value

当CR=CI/RI<0.1，表示该判断矩阵具有满意的一致性，否则需要对判断矩阵的元素值进行修正。

1.3 计算每个目标方案的单指标优度值

表4 0.1～0.9标度值及其含义Table 4 0.1～0.9 scaling value and meaning

(6)

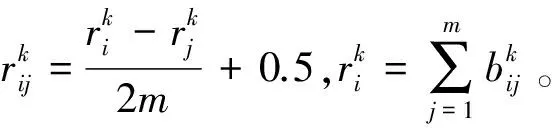
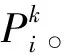
(7)

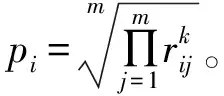
1.4 计算多指标下各目标方案的评价值

利用每个目标方案在单一指标评判下的优度值P及各指标的权重W，求取各目标方案的评价值：

(8)

根据Ki值大小，确定各目标方案的总体优势的排序，按分值最大最优原则选取。

2 工程实际应用

2.1 工程概况

黄桷湾立交是重庆市主城区最大、最复杂、功能最强大的立体交叉工程；该主线桥采用梁高2.5 m的预应力混凝土箱梁，由于箱梁截面采用斜腹板箱梁，箱梁外形比较美观；桥墩较高，除交界墩外，一般采用墩梁固接形式；下部结构采用钢管混凝土组合柱这种特殊结构形式的圆形墩。主线桥分左、右幅，左幅跨径布置：(30+35+40+35+40+50+40+35+33+40+40+35)m，全长为465 m；右幅跨径布置：(32.286+40+40+35+40+50+37+33+43+43+30+27.814)m，全长为466.6 m；单幅桥桥面宽9.50 m。该主线和地面之间高差比较大，桥墩较高，平均墩高约30 m。

2.2 主线桥上部结构施工方案

为了减少在施工期间对内环高速行车干扰，避免交通组织问题，对于主线桥，由于墩高，跨径大且变化较大，线形顺直，初步选择移动模架、贝雷梁门型支架和架桥机3种施工方法[6]，结合其经济性、风险性、施工工艺、适用性和工期共5种指标进行对比分析与综合评判，最终得出最适用、最合理的施工目标方案。因此，确定黄桷湾立交主线上部结构施工方法的AHP-FIE综合评价要素及模型，如图2，即：

T={移动模架T1, 贝雷梁门型支架T2,架桥机T3} ={T1,T2,T3}

U=经济性U1, 风险性U2,施工工艺U3,适用性U4,工期U5=U1,U2,U3,U4,U5

图2 黄桷湾立交主线上部结构施工的目标集和指标集Fig.2 Target and indicator set of Huangjuewan interchange mainline superstructure construction

2.3 基于AHP-FIE的施工方法进行优选

2.3.1 计算各指标的权重

1)构建层次结构模型

黄桷湾立交主线施工方法的评判指标主要由经济性、风险性、施工工艺、适用性和工期共5个方面组成，如图3。

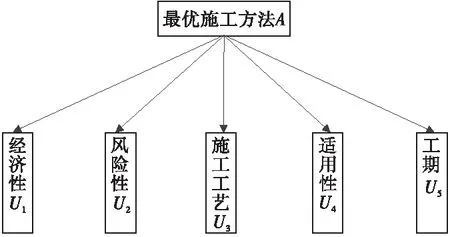
图3 层次分析模型Fig.3 AHP model

2)建立判断矩阵及计算权重

通过问卷调查、专家评审方式，确定各比较指标之间的相互重要性关系，得到判断矩阵A=(aij)n×n的相应元素的值，其中n=5，见表5。

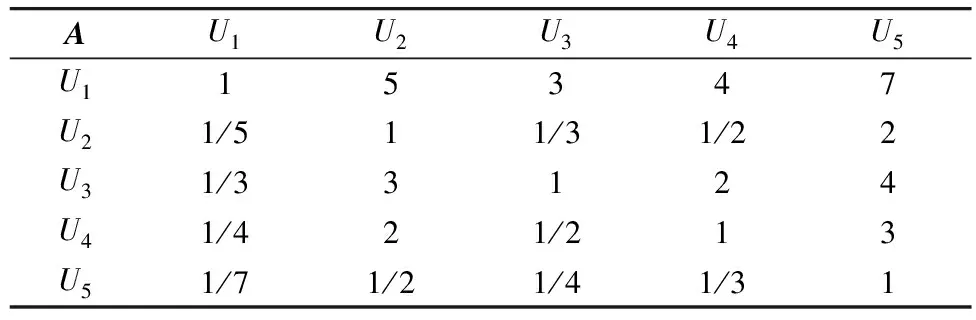
表5 判断矩阵ATable 5 Judgment matrix A

①计算判断矩阵A的每行元素连乘积的n次方根mi

mi=(3.347 0,0.581 8,1.515 7,0.944 1,0.358 9)T

②归一化处理，得各指标的相对权重值

W=(0.496 0,0.086 2,0.224 6,0.139 9,0.053 2)T

③计算判断矩阵A的最大特征向值

3)判断矩阵的一致性检验

①计算一致性指标

②计算一致性比例

CR=CI/RI=0.017 3<0.1，满足一致性检验。

2.3.2 计算每种施工方法的单指标优度值

现分别从评判指标的5个方面对移动模架、贝雷梁门型支架和架桥机3种施工方法进行分析、对比，得到各目标优度比较模糊矩阵B；经过一系列转化、运算，从而得到各目标方案的优度值集。

MSS移动模架施工[7]是使用支撑于桥墩的不着地移动式的支架和装配式的模板进行连续逐孔现浇施工。其特点是使用方便，施工速度快，安全可靠，机械化程度高，节省劳动力，减轻现场工人的劳动强度，少占施工场地，不会受桥下各种因素影响，能周期循环施工，同时还适用于20～50 m跨径的弯、坡、斜桥的施工，其适用性好。但是，移动模架一次性投资较大，拼装与拆除都很复杂，大体积，高吨位，高作业面，任务艰巨，施工风险高，同时由于主线桥与内环高速路呈斜交，移动模架支撑系统与移动模架系统呈斜交状态，且受中央分隔带的限制，造成移动模架支撑实施困难，灵活性较差。

贝雷梁门型支架现浇法是在现有浇筑桥墩和施工临时墩上搭设贝雷梁支撑体系，并完成箱梁混凝土的浇筑。该法施工中支架虽为临时结构，但施工中需承受梁的大部分恒载，因此必须有足够的强度和刚度。其特点是梁的整体性好，施工平稳、可靠，不需要大型起吊设备，允许桥跨下通行，但需要大量施工支架和处理临时墩的地基基础，由于立交主线平均墩高23.9 m，临时墩稳定性风险高，同时也对高支墩采取防撞措施。

架桥机安装法[7]，即在孔跨内安装导梁，是以此作为支撑梁来架设梁体。其特点是既不受架设孔跨的桥高度的影响，又不受梁下条件的影响，对交通及环境适应性好，作业安全性强，可利用已完成的桥梁来运送相关材料、设备及节段，自动化程度高，改善劳动条件，提高劳动效率，架设速度快，同时梁段预制与桩基、桥墩施工同时进行，节省了大量时间，工期短。但是，需要在主线桥端头修建大型预制场地，对环境破坏性大，架桥机投资大，高吨位、高作业面，风险性高。

1)在经济性指标下，求解各目标的优度值

合理确定和有效控制具体桥梁施工工艺情况下的工程造价是桥梁施工的经济性评价的基本内容，桥梁施工工艺的经济性评价，也是控制整个桥梁建设总造价非常重要的一环，是施工方法优选的重要性评价指标。根据施工造价的人工费、材料费和机械使用费，现对3种施工方法进行施工费用分析，见表6。

表6 3种施工方法经济性比较Table 6 Economic comparison of three construction methods /万元

根据以上分析，贝雷梁门型支架施工造价最低，工料机费用合计2 669.70万元；移动模架施工造价最高，工料机费用合计2 825.22万元；架桥机施工费用处于两者之间；即T2稍微优于T3，T2明显优于T1，T3稍微优于T1。在指标U1下，求解各目标的优度值过程如下。

①在指标U1下，得到各目标优度比较模糊矩阵

②将上式化成模糊一致矩阵

③计算目标Ti在指标U1下的优度值

2)在风险性指标下，求解各目标的优度值

风险性指标主要考虑施工设备出现风险事态的概率和损失，根据风险事态的等级来判断施工设备风险性大小。施工设备事故的可能性评估指标主要基于施工设备坍塌和失稳等。现对3种施工方法(T1，T2，T3)相应的施工设备发生施工事故的可能性评估指标体系进行取值打分，并且根据分值确定事故可能性等级，列出事故损失估计，根据风险矩阵法确定风险事态的等级[8]，见表7～表11。

表7 移动模架施工事故可能性评估指标体系Table 7 Accident possibility evaluation index system in mobile formwork construction

(续表7)

序号评估指标分类分值得分3节段尺寸节段长度35m以上(不含)或节段宽度15m以上(不含)1～3节段长度35m以下(含)或节段宽度15m以下(含)0～124气候环境条件极端气候事件多发区域(强风、强暴雨雪等)3～6气候环境条件一般，可能影响施工安全，但不显著1～3气候条件良好，基本不影响施工安全0～115设计与制作采用专业设计验证方案或相关合格且可靠产品0～1采用经验设计方案1～31合计p8

表8 支架现浇法施工事故可能性评估指标体系Table 8 Accident possibility evaluation index system in support cast-in-place construction

表9 架桥机施工事故可能性评估指标体系Table 9 Accident possibility evaluation index system in bridge erector construction

表10 3种施工方法的事故损失评价Table 10 Accident damage assessment of 3 construction methods

表11 3种施工方法风险评价Table 11 Risk Assessment of 3 construction methods

根据以上分析，因风险等级越小，则目标越优，得T3与T1稍微优于T2，而T1与T3等优。在指标U2下，求解各目标的优度值过程如下。

①在指标U2下，得到各目标优度比较模糊矩阵

②将上式化成模糊一致矩阵

③计算目标Ti在指标U2下的优度值

3)在施工工艺指标下，求解各目标的优度值

施工工艺指标主要包括施工技术的成熟度、施工单位对该施工方法的操作熟悉度和施工工艺的复杂性3个方面；贝雷梁门型支架浇筑是城市立交桥施工的常用方法之一，施工单位对该施工工艺具有良好的掌握性与操作性，经验丰富；架桥机安装法与移动模架浇筑法都是利用大型施工设备，其安装与拆除过程复杂，质量与精度较难控制，且移动模架吨位更大、现场浇筑大体积混凝土，施工工艺要求更高。

根据以上分析，在施工工艺指标U3条件下，T2稍微优于T3，T3稍微优于T1，T2明显优于T1；求解各目标的优度值过程如下。

①在指标U3下，得到各目标优度比较模糊矩阵

②将上式化成模糊一致矩阵

③计算目标Ti在指标U3下的优度值

4)在适用性指标下，求解各目标的优度值

适用性指标主要是对复杂环境的适用性(如生态环保、施工条件、桥下通行等)，由于主线桥与内环高速路呈斜交，移动模架支撑系统与移动模架系统呈斜交状态，且受中央分隔带的限制，造成移动模架支撑实施困难，灵活性较差，同时不会受桥下各种因素影响，对环境影响较小；贝雷梁门型支架现浇法通过架设临时墩，允许桥跨下车辆通行，但对桥下视野和安全有影响；架桥机安装法需要在主线桥桥头修建大型预制场地，对环境破坏性大，同时不受架设孔跨的桥高度的影响，又不受梁下条件的影响，对交通及环境适应性好。

根据以上综合分析，在适用性指标U4下，T3稍微优于T2，T2稍微优于T1，T3明显优于T1；求解各目标的优度值过程如下。

①在指标U4下，得到各目标优度比较模糊矩阵

②将上式化成模糊一致矩阵

③计算目标Ti在指标U4下的优度值

5)在工期指标下，求解各目标的优度值

移动模架施工和贝雷梁门型支架浇筑是严格按照施工工序，一步一步进行，箱梁现场浇筑需要在桥墩浇筑完成后，支架和移动模架架设好后，且完成预压才进行施工，且支架搭设比移动模架用时多，工期较长；而架桥机安装法的主梁浇筑与其他工序(如桩基、桥墩施工等)平行作业，互不影响，同时架桥机架梁速度快，节约了大量时间，因此架桥机安装法施工工期最短。

根据以上分析，在工期指标U5下，T3稍微优于T1，T1稍微优于T2，T3明显优于T2；求解各目标的优度值过程如下。

①在指标U5下，得到各目标优度比较模糊矩阵

②将上式化成模糊一致矩阵

③计算目标Ti在指标U5下的优度值

2.3.3 计算多指标下各目标方案的评价值