多类型异构无线网络连通性研究*

郭敬元，杨 涛，冯 辉，胡 波

（复旦大学电子工程系 上海200433）

1 引言

随着网络中越来越灵活的接入需求的发展，不同类型的用户终端之间的交互变得越来越频繁，网络也越来越多地体现出异构和动态的特性。异构性体现在网络中用户节点类型和分布的不同；动态性体现在自组织网络可以靠节点之间的通信组织相连网络，而不需要中心节点进行协调。典型的例子是认知无线电技术，主用户和次用户之间通过机会频谱共享进行交互。近年来，连续渗流理论[1]的发展和在全局网络行为方面的应用得到了重视。对于同构的自组织网络的连通性已有很多研究[2～6]，但对于异构网络，只有零星的文献有所研究，其中Ren W等人[7]定义了连通区域的概念，并推导出以节点密度、干扰范围和传输范围形式给出的连通性充分和必要条件，首创了将机会频谱的占有和释放与布尔渗流模型中的连通分量和空分量进行耦合求解。而对于次用户之间的合作对连通性的影响，Chon W[8]将异构网络建模为多个自组织网络，得到噪声受限和干扰受限普通衰落信道条件下的平均度和度分布，并以此为基础分析了合作渗流。参考文献[9]引入了认知无线电图模型，并考虑可用信道的个数和活动的主用户，由此得出在满足次用户网络渗流前提下的主用户临界密度。Wang P等[10]考虑到动态连接对连通性的影响，证明如果次用户密度大于一个临界值，则网络在任意时刻都可以保持连通，即使网络一直经历动态变化；还证明即使在任意时刻整个次用户网络是不连通的，也有可能存在一条时延通路使得某个次用户以概率1发送信息到目的地，而这一时延与发送端到接收端的欧式距离呈渐进线性关系。

网络连通性的研究，分为有限范围和无限范围，本文研究后者。从渗流角度研究无线多跳网络的连通性，主要特点是连通性取决于某个参数，渗流模型的分量可能有两种情况：所有连通分量全部有限；存在一条无限长的连通分量。后者被定义为无限网络的连通。

网络连通性研究的目标就是要找到使得网络能够连通的条件，参见如下连通性的定义：如果网络中存在一条无限长的连通分量，则称网络是连通的。所谓无限长的连通分量，指图中无限长的由节点连接而成的一个分簇，只要存在无限长连通分量的概率不为0，就认为网络是连通的。

网络渗流的概念是从物理学领域发展出来的，指的是从无连通分量到出现连通分量的相变过程，即物质在外部参数（如温度、压力等）的连续变化之下，从一种相忽然变成另一种相，最常见的是冰变成水。将网络渗流应用到信息科学领域，通过随机几何图实现。随机几何图描述了点和边的关系，点和边的分布以及边和边的连接方式决定了一个随机几何图的性质，点的分布服从某个特定的点过程。点过程是从概率空间到某空间E上的点度量空间的映射Φ，点度量是局部有限的，且只取整数值，表示如下：

其中，δXi是狄拉克测度，Xi是随机变量，在E上取值，是d维欧几里德空间,d≥1。连续渗流领域普遍采用的模型是泊松点过程分布的点，当且仅当它们之间的距离不超过r时，这两点相连，记为G（X，r）。虽然泊松分布过程被广泛用作分析随机网络连通性，但并不总是符合实际情况，簇分布被证明更加接近城市热点地区的实际情况[11,12]，不过此类分布的连通性仍然未知。常规的异构网络分析主要侧重于两类异构用户，即主用户和次用户之间的交互行为，但实际上次用户也是由多种类型的终端构成的，如具有不同传输范围的终端。本文通过对单类型节点和多类型用户节点组成的异构网络的分析，推导网络的连通性与各参数之间的影响。

2 网络模型与应用

目前主要从两个角度进行网络连通性研究，分别是泊松布尔模型和随机连接模型。布尔模型中，点的分布随机，每个点的覆盖范围随机（连续渗流中采用固定大小圆盘模型），任意节点可以和自己覆盖范围内的所有节点连接；随机连接模型中，点的分布随机，但每个点并不是跟自己圆形覆盖范围内的节点连接，而是由一个随机连接函数决定与某一个节点进行连接。

从布尔模型和随机连接模型两个角度分别分析异构网络的连通性，其中布尔模型又分为单类型节点异构网络和多类型节点异构网络。对于每种模型，都有一个对应的实际应用网络进行举例分析，如移动自组织（Ad Hoc）网络、认知无线电。

2.1 布尔模型

2.1.1 单类型节点异构网络

Ad Hoc网络的连通性受到广泛关注。Ad Hoc网络是一种多跳的临时性自治系统，原型是美国早在1968年建立的ALOHA网络。作为一种分布式网络，Ad Hoc网络是一种自治、多跳网络，整个网络没有固定的基础设施，能够在不能利用或者不便利用现有网络基础设施（如基站、AP）的情况下，提供终端之间的相互通信。由于终端的发射功率和无线覆盖范围有限，距离较远的两个终端如果要进行通信就必须借助于其他节点进行分组转发，这样节点之间构成了一种无线多跳网络。

简单地用泊松分布分析Ad Hoc网络过为理想化，因为假定所有用户节点平均分布在有限区域中不太符合实际情况。实际的用户节点分布经常是在某些热点地区稠密，在其他非热点地区稀疏，从而可引出簇分布，即用户节点有向各个中心节点靠拢的趋向。分析单类型用户时，用簇分布中的一种——Thomas分布模拟真实用户节点分布。

当次用户只有一种类型（即所有次用户传输范围相同）且分簇分散在各处时，研究临界点与其他簇分布参数的关系。采用Thomas点过程作为簇分布的模型，图1(a)为一个Thomas过程在单位方格中的示例。在Thomas过程中，节点分为两类：一类是簇头节点，即中心节点，如图1(a)中的“”点，服从泊松分布，均匀密度为λ；另一类是围绕在各个中心节点周围的普通节点，如图1(a)中的黑色圆点，服从高斯分布，均值为μ，协方差矩阵为σ=diag(σx,σy)，图1(a)中的圆圈是以中心节点为圆心、某个固定的σ=σx=σy为半径所做的圆。所有普通节点都可作为发送端和接收端，传输范围均为r。

直观来说，当节点分布从泊松分布扩展到Thomas分布时，渗流产生将变得更加困难。原因在于随着进一步的聚簇，越来越多的内部节点的连接效应会递减，直到逐步发展到全局连通性主要由每个簇的边缘节点决定。一旦这些边缘节点可以连接相邻的簇的边缘节点，这两个簇就可以连通。从这种思路出发，引用平均场估计 （mean field approximation）理论推导传输半径的临界值。平均场估计理论被用来分析多体物理系统中的交互行为，用均值代替所有交互，将多体问题有效地简化为单体问题。建模时将所有周边信息视为一个统一的变量，并将所有的残余节点视为确定性的平均场，本质即统计均值。

对于Thomas过程而言，可以把簇的内部和外部的节点等效为一个半径确定但未知的圆，使得这些节点等效于这个圆上某些均匀分布的点（如图1(b)所示）。根据参考文献[13]，可以先得到圆内点的距离分布以及圆上点的平均距离（即圆上点的个数）。假设两个簇的等效圆上各有3个均匀分布的节点，为了研究这两个簇之间的随机连通性，假定左边的簇O1固定，让右边的簇O2以簇头为中心，沿某方向转动。当总存在至少一个节点在弧de上时，则总存在一个节点c可以连接到O2的边缘节点，以使两个簇连通，途经节点{a，b，c，d，e}。

2.1.2 多类型节点异构网络

单一类型的簇分布的用户节点并不能反映其他一些重要的实际场景，应当引入混合类型的用户节点。例如在认知无线电中，有主用户和次用户两类，而次用户本身也可能有多种类型。考虑到理论分析的可行性，构建以下泊松分布的认知无线电模型。

无限的二维欧式空间中，泊松分布的次用户网络叠加在泊松分布的主用户网络上。这与同构网络有着显著的区别，即多类次用户节点之间通信链路的存在与否不仅取决于它们之间的距离，还跟周围主用户的特征（荷载、拓扑、干扰容限）和收发行为有关。

假设主用户发射端以密度为λp的二维泊松点过程分布，对每个主用户发射端来说，它的接收端均匀分布在传输距离为Rp的范围内。假定所有主用户发射端的发射功率相同，信号经过相同的路径损耗，则主用户接收端也以密度为λp的二维泊松点过程分布且与发射端点过程相关，主用户对周围次用户的干扰范围是RI。

次用户叠加在主用户之上，也服从泊松分布，分为两类（T1与T2），具有混合密度λs，即T1次用户密度为pλs，T2次用户密度为（1-p）λs，传输范围分别是rp1、rp2，干扰范围分别是rI1、rI2。以参考文献[7]中的模型为参考，并拓展到两类次用户的情况，构建次用户之间的双向连接，如图2所示。

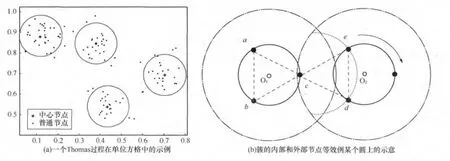
图1 Thomas过程

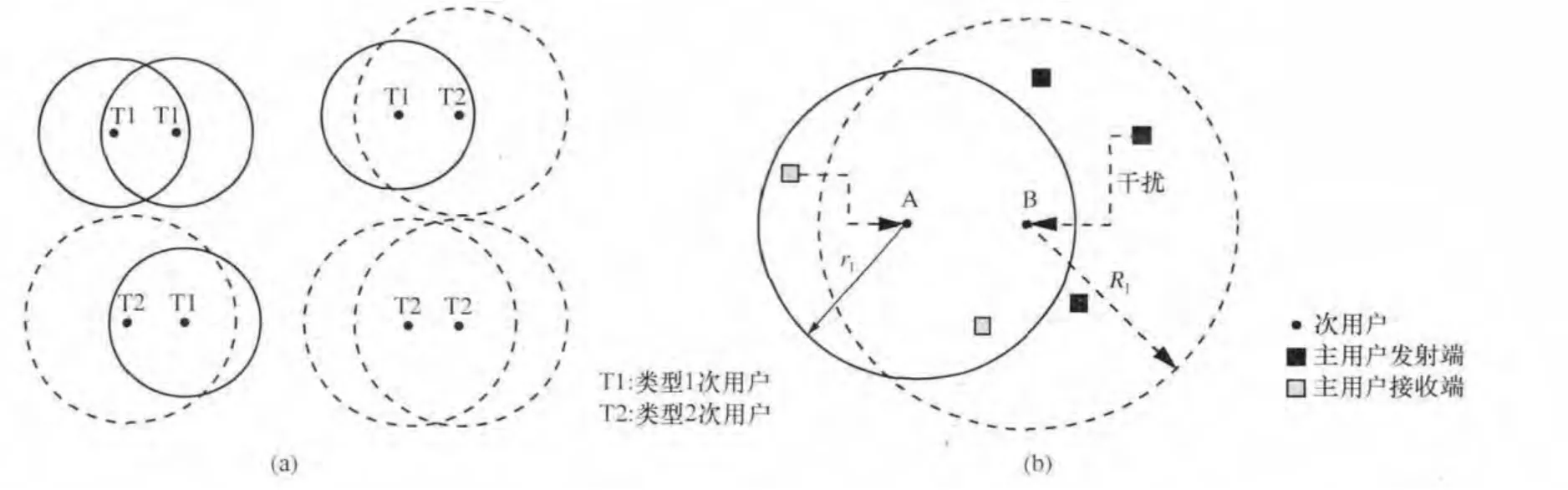
图2主用户与次用户示意

图2 (a)中，次用户A到次用户B的通信链路可分为4种情况：T1→T1、T1→T2、T2→T1、T2→T2。图2(b)为T1→T2放大后的详细情况。为了解决网络连通性的问题，构建随机场多类型分支（MBPR）过程，从理论上推导分布参数对网络连通性的影响。可以想象，从某个用户节点S1开始，把与之相连的用户节点组成的连通分量“提起来”变成一棵以S1为根的树（如图3所示），这样无限长连通分量的存在性就等价于这棵树（分支过程）能否无限生长下去。问题的本质就是，随机场如何决定树的每一代的复制分布。如前所述，用户的不同类型指的是不同的传输半径，从而MBPR可以被归结为具有不同传输半径的用户能否通过合作使得这棵树无限延伸，由此引出两类次用户连通的必要条件。当有更多类型的次用户时，可以方便地从两类次用户进行拓展。

图3 多类型分支过程

定理 以上定义的混合次用户网络能够发生渗流的必要条件是：

证明 基本思路是构建一个MBPR，每个节点都分别对应一个类型t∈T={1，2}，每个节点都可以“生出”任意类型的子节点，即任意次用户都可以和满足以下条件的T1和T2次用户进行通信。

·条件1：它们之间的距离至多为max{rp1，rp2}；

·条件2：它们之间存在双向机会频谱，即次用户A的rI1或rI2范围内无主用户接收端，RI范围内无主用户发射端，见图2(b)。

对于每个节点来说，如果它属于类型t，则有一个与它关联的随机向量ζt={ζt1，ζt2}，其中ζtj是一个随机变量，表示由第t类节点产生第j类节点的个数。把它的期望记为mij，则一阶矩量矩阵可由A构建。根据参考文献[16]的定理，MBPR在ρ=1、ρ<1、ρ>1时分别为临界、次临界和超临界状态，其中ρ是矩阵A的谱半径，即A的最大正特征值。

在上述分支过程中，矩阵A的4个元素可以用与参考文献[7]类似的方法求得，式(4)给出m12元素的求解，其他3个元素可采用类似方法求得。

图4 SI2（r，θ，Rp，t，rI1，rI2）为阴影部分

2.2 随机连接模型

用圆盘模型进行理论分析较为方便，但在实际应用场景中，由于功率限制与通信干扰及能量消耗等因素，用户节点并不可能跟通信范围内的所有节点都建立连接，而只能跟通信范围内的某些节点建立连接。此场景可抽象为由随机连接函数决定节点间连接的随机连接模型。先介绍不考虑用户节点间距离的Erd仵s-Rényi（ER）模型，再扩展增加距离约束。

在图模型中，ER模型指在每一对节点中，都以相同的概率p存在一条边。近年来，Achilioptas过程因为能够提前或推迟渗流相变的发生而受到很多关注。在2000年的一个会议中，Achlioptas D提出，从一个没有边的图出发，每一步从所有可能的边中找到两条独立的边e1和e2，再根据“乘积规则”[15]选择两条边的一条进行连接。而“乘积规则”，就是通过选择边的两点所在分量的度的乘积大的一条，选择对应的边。问题在于：乘积规则会对产生的边的大小有何变化？对图的渗流有什么影响？这里给出一个仿真来展示ER模型和乘积规则对于Thomas过程临界行为的影响。

如图5(a)所示，横坐标为次数，即每次根据乘积规则添加一条边，纵坐标为最大连通分量的大小。可以看到，乘积规则会一开始推迟相变的发生，最大连通分量一直保持较小的增长，直到到达临界点，最大连通分量迅速增大到90%以上，产生爆炸效应，从ER模型的一阶相变变为二阶相变，这种选择方法产生所谓的“爆炸渗流”现象。

更进一步考虑爆炸渗流，一种方法是增加距离约束，即让两个用户节点之间的连通概率与距离有关。一般连通性会随着距离的增大而减少，而是否连通取决于两个节点在实际网络中的真实距离，这样乘积规则就可以修改为增加距离参数，即选择以下值：

这被称为“最小引力规则”，用来衡量距离对最大连通分量出现的影响。其中，d是一个可调参数，衡量距离对乘积规则的影响，M1与M2表示第一条边的两个节点所对应的连接分量的大小，R12表示这两个点的距离，M3与M4表示第二条边的两个节点所对应的连接分量的大小，R34表示这两个点的距离。引入距离对爆炸渗流的影响如图5(b)所示，其中粗线表示ER模型，其他7条曲线分别是d从1～7时的乘积规则模型，随着d的增大，爆炸特性逐渐减少。可以推测存在某种标度，当d趋于无穷大时，爆炸渗流趋于ER模型。

3 仿真试验与分析

使用蒙特卡洛仿真验证第2.1节中二维Thomas过程的临界连接现象，目的是研究何时以及在哪里会发生渗流、不同参数之间的交互如何影响相变的发生。通过有限尺度的标定，首先设置初始值，在单位方格内以Thomas分布确定点的位置。保持3个参数不变而改变另一个参数，得到如图5所示的观察结果，其中，纵坐标是最大连通分量所占总节点个数的比例，横坐标是对应的改变参数。

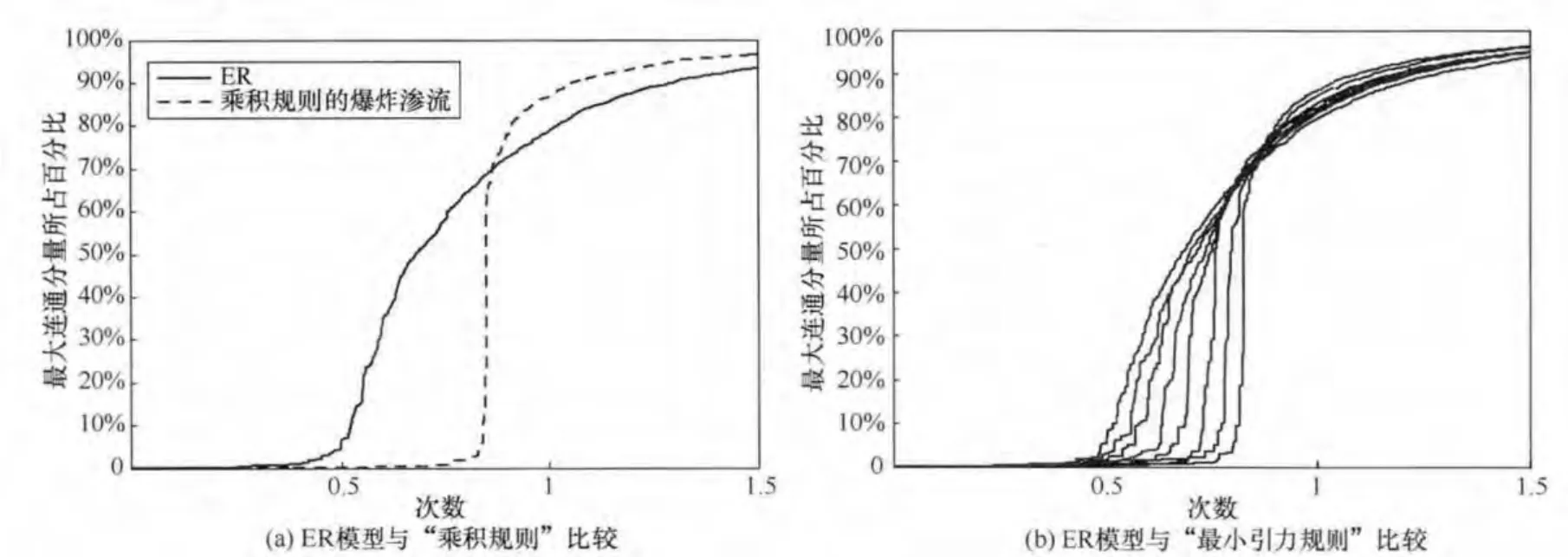
图5 两种爆炸渗流模型相变比较

图6(a)是通信范围r对连通性的影响。显然，如果不要求全连通，则可以显著地减小r。聚簇参数σ对最大连通分量的影响较微小，因为较小的σ会加速最大连通分量的出现。图6(b)是μ对连通性的影响，可以看出，增大μ对于增强网络连通性的效率不高，原因是这只是增大了簇头节点周围的平均节点数目，如果没有增大λ，连通性很难通过只扩大每个簇的节点数而提高。图6(c)是λ对连通性的影响，因为增大λ不仅会增加簇头点数，而且还有附带的周围节点，密度参数λ对整个网络连通性的影响最大。图6(d）是σ对连通性的影响，这个参数的影响比其他几个参数更复杂些，随着σ的增大，最大连通分量的大小先增后减。

寻找临界值rc、λc较为困难，可以从工程应用角度拟合得到rc的近似值。拟合的一种方法是对图6(b)曲线中的μ进行微分，寻找最大的斜率点r作为临界值rc并与每个μ对应，从而得到二阶对数多项式拟合。

4 结束语

从渗流角度研究了自组织异构通信网络的连通性问题，分别从布尔模型和随机模型的角度出发，对单类型用户网络和多类型用户网络在不同场景下进行建模，从理论推导和仿真的角度分析了认知无线电系统中次用户网络的连通性。上述研究对多类型异构网络的部署与设计具有一定的指导意义。

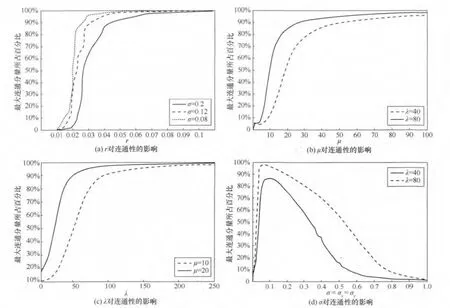
图6 各参数对最大连通分量的影响

1 Meester R,Roy R.Continuum percolation.Cambridge University,1996

2 Cheng Y C,Robertazzi T G.Critical connectivity phenomena in multi-hop radio models.IEEE Transactions on Communications,1989,37(7)

3 Dousse O,Baccelli F,Thiran P.Impact of interferences on connectivity of Ad Hoc networks.ACM/IEEE Transactions on Networking,2009,13(2):425～436

4 Dousse O,Franceschetti M,Macris N,et al.Percolation in the signal to interference ratio graph.Journals on Appl Prob,2006(43):552～562

5 Kong Z,Yeh E.Connectivity,percolation,and information dissemination in large-scale wireless networks with dynamic links.IEEE Transactions on Information Theory,2009(1)

6 Vaze R.Percolation and connectivity on the signal to interference ratio graph.Proceedings of the IEEE Conference on Computer Communications(INFOCOM 2012),Orlando,Florida,USA,March 2012

7 Ren W,Zhao Q,Swami A.Connectivity of heterogeneous wireless networks.IEEE Transactions on Information Theory,2011,57(7):4315～4332

8 Ao W C,Chen K C.Cognitive radio-enabled network-based cooperation:from a connectivity perspective.IEEE Journal on Selected Areas in Communications,2012,30(10):1969～1982

9 Lu D,Huang X,Li P,et al.Connectivity of large-scale cognitive radio Ad Hoc networks.IEEE INFOCOM,2012(1)

10 Wang P,Akyildiz I F,Al-Dhelaan A M.Percolation theory based connectivity and latency analysis of cognitive radio Ad Hoc networks.Wireless Networks,2011(17):659～669

11 Li D,Gross J.Robust clustering of Ad Hoc cognitive radio networks under opportunistic spectrum access.Proceedings of IEEE International Conference on Communication,Kyoto,Japan,Jun 2011

12 Liu S S,Lazos L,Krunz M.Cluster-based control channel allocation in opportunistic cognitive radio networks.IEEE Transactions on Mobile Computing,2012,11(10):1436～1449

13 Srinivasa S,Hartin M.Distance distributions in finite uniformly random networks:theory and applications.IEEE Transactions on Vehicular Technology,2010,59(2):940～948

14 Erdos P,Renyi A.On the evolution of random graphs.Publ Math Inst Hungary Acad Sci,1960(5):17～61

15 Achlioptas D,Souza R M D,Spencer J.Explosive percolation in random networks.Science,2009(323)

16 Serra M C.A Multi-Type Branching Processes Approach to the Evolutionary Dynamics of Escape,2007