基于用户相关数据的乘用车试验场变速强化试验方法*

门玉琢，于海波，郭 平，董立甲，韩 愈，张元勤

(1.长春工程学院机电工程学院，长春 130012； 2.中国第一汽车股份有限公司技术中心，长春 130011)

前言

汽车耐久性试验是考核和验证其可靠性的一种重要手段，由于在普通路面上做行驶试验直至薄弱环节失效，一般要行驶几万甚至十几万km。为缩短可靠性试验时间，试验场试验条件变得越来越苛刻，这主要通过建造更恶劣的试验道路和加快行驶车速来实现[1-2]。在20世纪50年代，人们认识到试验场的试验条件过于苛刻并不合理，因为它会引起一些在用户实际使用中不会出现的失效模式而造成误导。现代汽车设计必须以市场为导向，设计寿命“过长”或“不足”的产品通常是不经济且缺乏市场竞争力的，所以无论在汽车设计、开发或试验阶段都应当考虑用户的实际使用要求[3-4]。动力传动系作为汽车的一个重要总成，其可靠性对行车安全至关重要，制订科学、合理的符合用户使用条件的可靠性试验规范且能对试验结果进行科学评价，是整个汽车行业面临的一个重要课题。

1 试验方法机理

计算用户实际使用环境中动力传动系各级转矩对应的疲劳损伤，在试验场变速强化路重现的等价损伤通常可在较短的时间内完成，因此可达到传动系强化试验的目的，其相关性研究方法见图1。

1.1 实际用户数据调查

研究用户使用情况与试验场变速强化路试验之间的相关性，制订科学、可信的变速强化试验方法，须在全国范围内调查与本次试验车型相关的车辆用户使用信息[5]。对用户和潜在用户使用情况进行调查、访问，内容主要包括用户使用的路面类型比例、行驶车速、交通状况、车辆负荷情况、行驶道路种类、各种道路的行驶里程、驾驶习惯和各种典型道路所在地区等内容，调查结果如图2所示。

将用户调查数据作为参数变量，输入90%用户模型进行计算，对计算结果进行Monte-Carlo仿真模拟获得用户目标里程疲劳损伤。

1.2 90%用户累积损伤模型

对于用户使用的4种典型路面(城市路面、高速公路、郊区路面、一般公路)和试验场变速强化路，传动系的疲劳损伤服从Weibull分布[6]，其分布函数为

(1)

式中：F(t)为累积分布函数；t为传动系损伤；β为尺度参数；m为形状参数。

Weibull分布参数可利用最小二乘法估计，将式(1)改写为

(2)

Y=mX+b

(3)

其中：b=-mlnβ。

因此，Weibull分布模型参数的最小二乘法估计结果为

(4)

根据Weibull分布概率纸的直线方程与实际用户调查数据(行驶路面比例和载质量)，对于用户使用的典型路面，失效概率为90%的用户动力传动系疲劳损伤计算模型为

(5)

式中：Wai为载质量调整因数；fci、fei、fti和fgi分别为用户调查城市路面、高速公路、郊区路面和一般公路的百分比；Dc、De、Dt和Dg分别为城市路面、高速公路、郊区路面和一般公路的90%用户疲劳损伤；Di为第i个90%用户总疲劳损伤；n为用户调查样本总数。

1.3 目标用户的Monte-Carlo仿真

针对要求解的90%用户目标总疲劳损伤，建立一个正态分布统计模型，使所求的解恰好是该概率统计模型的数学期望[7-8]。利用式(5)计算的90%用户路面的总损伤服从正态分布，可建立正态分布的随机抽样模型进行模拟。由RAND(·)函数产生两组均匀分布于(0，1)上的独立随机数r1和r2，并做如下变换：

(6)

其逆变换为

(7)

可导出y1、y2的联合分布密度函数为

(8)

显然，概率密度分布函数y1与y2相互独立，且均服从标准正态分布，即yi～N(0,1)。对任意均值为μ、方差为σ2的正态分布随机变量xi可通过以下变换得到：

(9)

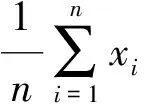
(10)

式中α为显著性水平。

因此，Monte-Carlo仿真误差为

(11)

对于给定的显著性水平α，tα可通过查标准正态分布函数数值表求得，所以Monte-Carlo仿真误差由方差和抽样次数决定。

利用式(9)变换抽样法产生服从正态分布的随机样本，仿真抽样求出90%用户目标损伤。模拟计算次数越多，统计量的平均值越接近真实值。

2 变速强化试验方法

变速强化试验实际上就是换挡强化试验，主要在3种工况下进行：(1)连续升降挡，以5挡变速器为例，即按1、2、3、4、5挡的顺序升挡，然后再按5、4、3、2、1的顺序降挡；(2)奇数升降挡，对于5挡变速器，即按1、3、5挡的顺序升挡，再按5、3、1挡的顺序降挡；(3)偶数升降挡，对于5挡变速器，即按2、4挡的顺序升挡，再按4、2挡的顺序降挡。

2.1 传动轴转矩测量

传动轴作为动力传动系的主要部件，其输出转矩是可靠性试验中重要的测试参数，本文中应用J1型单通道非接触式转矩传感器测量转矩，如图3和图4所示。

2.2 数据分析与处理

将传动轴转矩对转速进行分级计数，转化成不同转矩、转速下的转动次数或转数分布矩阵。利用传动轴转矩分级计数矩阵，可计算每种路面和每个文件的各级转矩对应的传动轴疲劳损伤，见图5和图6；3种工况的损伤计算结果见表1。

2.3 Weibull分布参数估计

为了在Weibull分布模型中描绘其分布曲线，可应用中位秩公式计算传动系损伤的概率估计值。

试验工况单次循环里程/km循环次数单次循环累积损伤单位里程损伤工况1518282685×10-90518×10-9工况2373322805×10-90752×10-9工况3861821675×10-90194×10-9

(12)

式中：n为样本容量；i为样本排列序次。

根据传动轴转矩产生的疲劳损伤排序和估算概率，应用最小二乘法估计的Weibull参数值见表2。利用Weibull概率纸拟合的直线方程，计算所有调查用户的每种路面90%用户疲劳损伤见表3。

表2 Weibull参数的最小二乘法估计结果

表3 90%用户和变速强化路损伤计算结果

结合用户调查路面比例，利用式(5)90%用户损伤模型计算每个用户的损伤，Monte-Carlo仿真模拟90%用户目标损伤为1.178×10-6，仿真抽样次数为10 000次，取置信度为95%以保证Monte-Carlo仿真算法的抽样精度，此时仿真误差为0.78%。

2.4 变速强化系数

强化系数是变速强化路的可靠性试验和用户实际使用情况相比较而言的，车辆的动力传动系损伤在规定的条件下且疲劳损伤相等时，用户普通路面与变速强化路可靠性试验的行驶里程之比，即

(13)

式中：K为强化系数；d为90%用户目标行驶里程；R为变速强化路一个试验循环总里程；Ea为90%用户目标里程损伤；Eb为变速强化路一个试验循环的里程损伤。

以50 000km定义为用户目标行驶里程，由式(13)求得的变速强化路传动系的强化系数为19.2。计算变速强化路传动轴转矩疲劳损伤，对于3种试验工况，考虑到转矩单次循环累积损伤、单位里程损伤和整个试验周期，变速强化路3种试验工况单个循环行驶里程为66km，共计600个循环(总试验里程为39 600km)，传动系产生的疲劳损伤等效于用户实际使用760 000km。

3 结论

基于传动轴转矩疲劳损伤等效原理，建立了90%用户传动系损伤计算模型，对传动轴转矩及其对应转速采取分级计数处理，利用最小二乘法估计出Weibull分布参数。结合实际用户调查数据，应用Monte-Carlo仿真方法获得90%用户的总损伤。通过对变速强化路和用户数据相关性分析，获得相对于用户路面的强化系数和传动系等效寿命里程，为评价和考核传动系可靠性提供了新的试验方法。

[1] 门玉琢,于海波,韩愈.用户相关汽车动力传动系可靠性试验新方法[J].振动与冲击,2013,32(11):25-29.

[2] Bannantine J A, Comer J J, Handrock J L. Fundamentals of Metal Fatigue Analysis[M]. New Jersey: Prentice Hall, Englewood Cliffs,2004:182-184.

[3] 门玉琢,李显生,于海波.与用户相关的汽车可靠性试验新方法[J].机械工程学报,2008,44(2):225-226.

[4] Campean F. Vehicle Foresight Customer Correlation of Engine Components Tests Using Life Prediction Modeling[C]// SAE 2002 World Congress. Michigan: Society of Automotive Engineers,2002:110-112.

[5] Muddiman M W, Moore G R. Structural Correlation of Automotive Proving Ground to China Customer Field Usage[R]. USA: UltiTech Corporation,2003.

[6] 洪延姬,李俊美,王志魁,等.寿命服从威布尔分布产品相关失效数值分析[J].装备指挥技术学院学报,2002,13(5):33-34.

[7] 吴飞.产生随机数的几种方法及其应用[J].数值计算与计算机应用,2006(1):49-50.

[8] 袁贵星,王平.蒙特卡洛模拟及其在公差设计中的应用[J].天津科技大学学报,2008,22(3):62-63.