基于雷达测距的车辆识别与跟踪方法*

周俊静，段建民，杨光祖

(北京工业大学电子信息与控制工程学院，北京 100124)

前言

实时准确地检测前方车辆的速度、位置等信息是汽车防碰撞预警和自适应巡航控制等汽车辅助驾驶系统实现的前提。由于道路行驶的复杂性，车辆检测和跟踪算法的鲁棒性显然是衡量系统性能的重要指标。

本文中介绍一种基于激光雷达的前方车辆检测和跟踪算法，该算法将作为多传感器融合智能车辆环境感知系统的重要组成部分。

文献[1]中通过提取车辆目标的直线和直角特征来识别车辆，从而克服了目标形状变化的干扰。但该算法采用固定距离阈值的方法进行聚类，在聚类过程中会丢失远处入射角较小的目标上的点，不仅影响到特征提取的准确性，而且在后续的目标跟踪过程中会产生较大的测量误差。文献[2]中提出了一种用于激光雷达数据的自适应改变距离阈值的聚类方法，该方法可根据扫描点与传感器的远近自动调整距离阈值，但对目标与传感器的相对方位变化不敏感。

多目标跟踪的关键问题是目标间的关联。目标关联的方法包括两大类：确定性方法和概率统计方法[3]。文献[4]中采用确定性方法进行运动目标的关联，所提出的跟踪算法能够处理遮挡和漏检的问题，文中假定被跟踪目标的数目是确定的，从而不能处理新目标出现和目标消失的情况。

概率统计目标关联的方法主要针对采集到的环境信息中包含大量杂波和目标的机动性大的情况，具有代表性的方法包括联合概率数据关联(joint probability data association, JPDA)和多假设跟踪(multiple hypothesis tracking, MHT)[2]。JPDA须计算被跟踪的目标和当前帧中真实目标的测量值和虚假目标之间的联合概率，计算量非常大，且同样假定被跟踪的目标数目是确定的。文献[5]中提出了MHT方法，它能够处理新目标出现和目标消失的情况，但要保存连续几帧数据中每一个目标所有可能的关联，因此计算量和内存开销都非常大。

本文中采用基于距离的方法对雷达数据进行聚类，在文献[2]中提出的自适应距离阈值聚类方法的基础上，增加对目标和传感器的相对方位判断，距离阈值不仅与扫描点和传感器的距离有关，还与目标和传感器的相对方位有关，提高了聚类的准确性。

考虑到道路上行驶的车辆机动性较小，激光雷达的扫描频率可达每秒几十帧，在此期间车辆的位移变化微小，本文中采用确定性方法进行目标关联，代价函数的主要约束条件为目标的位置，同时考虑目标的大小、形状和长宽比，并用实际数据对模型进行了论证。

1 车辆识别

1.1 数据的预处理

本文中采用LMS291型激光雷达作为传感器，其主要参数见表1。它以线扫描方式来测量距离，每次扫描采集得到的数据包以极坐标形式表示为R={(rn,φn)|n=0,…,NR}，之后再转换为笛卡尔坐标。以大地平面为坐标系，车辆行驶的方向为y方向，与车辆行驶方向垂直，并指向右面的方向为x方向。

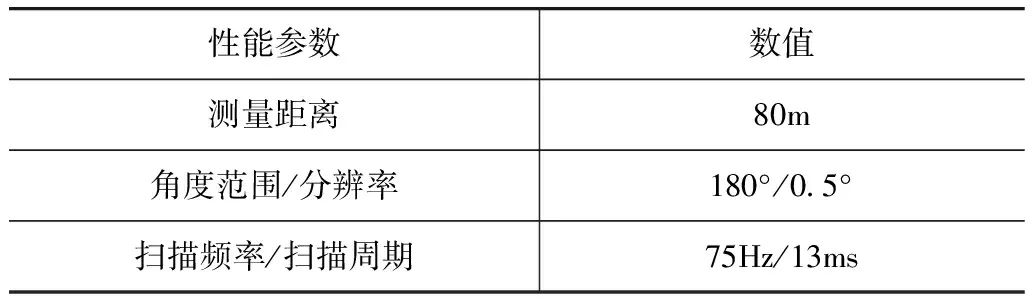
表1 LMS291激光雷达的主要性能参数

在实际检测中，一般可以扫描到车辆的一个或两个侧面，图1示出激光雷达所采集的深度信息。这里的“深度信息”指的就是雷达传感器至目标的距离。由图可见，与本车的距离较远的聚类3，其内部数据点间的实际间距明显比近处的聚类1和聚类2内部数据点间的间距大。另外，当扫描到车辆的两个面时，与扫描射线接近垂直的面上的点比较密集，但对于与扫描射线方向大致相同的侧面，由于入射角较小，所采集到的点比较稀疏，加上轮胎所在位置的反射率较低，通常这个面上的扫描点稀疏且不连续。

根据车载雷达系统的以上特点，本文中采用基于距离的聚类算法，距离阈值可以根据障碍物与传感器的距离远近和相对方位自动调整。算法的基本思想为：如果顺序采集到的两个数据点间的距离‖pn-pn-1‖大于一定的阈值Dmax，则认为这两个点是不连续的。由于随障碍物与传感器的距离增大，连续扫描到数据点间的距离也会增大，而车辆侧面的扫描点，即使与传感器的距离较近，相邻两点间的距离也比较大，因此阈值Dmax应该随障碍物距离的改变而改变。文献[5]中提出了一种自适应的改变阈值Dmax的方法，计算式为

(1)

式中：rn-1为pn-1点的深度值；σr为激光雷达的测量误差；Δφ为激光雷达的角度分辨率；λ为阈值因数，它决定了最大距离阈值的大小。λ的值一般通过经验得到。

如果对所有的数据点都采用相同的λ，目标车辆侧面上的点很可能和正面上的点不归到同一个聚类中。因此，在聚类过程中，首先计算连续两点的相对位置，对于处于车辆正面(与激光射线接近垂直的面)上的连续两点取较大的λ值，计算得到较小的距离阈值，处于车辆侧面(与激光射线接近平行的面)上的连续点则取较小的λ值，计算得到较大的距离阈值。

聚类完成后，对目标进行初步的分类，对于内部距离较小的目标，直接归类为非车辆目标。由于只是粗略估计聚类内部距离，因此计算聚类起点和终点之间的距离，假设起点为pni，终点为pne，则两点之间的距离为

(2)

1.2 特征提取和车辆识别

考虑到检测的目标为车辆，而激光雷达扫描到的车辆目标一般为一条直线或夹角接近直角的L形折线，本文中采用端点迭代拟合(iterative end point fitting, IEPF)算法[6-7]结合最小二乘法直接对聚类进行直线或折线拟合。该方法的特点是，可以根据聚类内部点的分布情况，将一个聚类分成一个或多个子集，对每个子集分别进行直线拟合。每个聚类内可以拟合出一条直线或一条折线。因此该算法可以准确地拟合出车辆的形状，特别是当激光雷达扫描到车辆的两个侧面时。

在每个聚类内部实施直线拟合算法，其一可以提高实时性，即不用在整幅图像内实施IEPF算法和直线拟合，其二可以避免将不同的聚类连在一起。

IEPF算法分两步：首先，将一个聚类内的扫描点分成几个部分，每个部分都可以拟合出一条直线；其次，对第1步中分出的每一个部分进行直线拟合，本文中采用最小二乘法拟合直线。

在聚类内部拟合出直线后，提取每个聚类的特征向量。特征向量包括目标的位置和几何特征，具体包含5个变量：(1)目标的位置 由于雷达数据的不完整性，很难准确估计目标的质心，本文中位置的参考点为，当扫描到目标车辆的一个面时，取直线的中点，当扫描到车辆的两个面时，取两个面的角点；(2)目标包含的线段数目，一般为1条或2条；(3)目标的形状 只包含一条线段的目标，计算直线与x轴的夹角，如果为车辆目标，夹角较小；包含两条线段的目标，计算两条线段的夹角，如果为车辆目标，夹角应接近90°；(4)目标的大小 对于具有一条直线的目标，计算直线的长度，对于具有一条L形折线的目标，计算最小包围矩形的面积；(5)目标的长宽比 当聚类内有两条直线时，计算两条直线的长度比。

根据提取到的特征向量，利用多特征融合的方法逐步对目标进行确认。确认过程如图2所示。图3为采用本文中聚类算法和采用固定距离阈值聚类算法的车辆识别结果的对比。图中的圆圈为聚类的起点和终点，两个圆圈之间的点为一个聚类，矩形框表示识别出的车辆目标。图3(a)与图3(b)为一组对比，图3(a)中采用可变距离阈值的聚类算法，能够准确地识别出扫描环境中的车辆。图3(b)中采用固定距离阈值的聚类算法，距离阈值取0.6m，只能识别出部分车辆目标，车辆目标1侧面上的点在聚类的过程中丢失，导致未能识别出该目标。目标2和目标7都被分割成了两个聚类，造成未能识别出目标2，而识别出的目标7为实际目标的一部分，这样在计算目标位置时会存在较大的误差，势必对目标跟踪造成不利影响。文献[1]中同样存在将同一目标分割成几个部分，而不能识别的情况。目标8～目标10与本车距离较远，因此扫描点间的距离较大，距离阈值取0.6m时不能聚类，也就未能识别。图3(c)与图3(d)为一组对比，图3(d)中距离阈值取1.5m，虽然能够比较准确地将车辆侧面上的点进行聚类，但由于距离阈值较大，距离较近的目标6和目标7被合并为一个目标。

2 目标车辆的跟踪

由于激光雷达的扫描频率较高，同一目标在连续两帧数据中位置变化很小，假设目标作匀速运动且过程噪声为高斯白噪声，对识别出的车辆目标利用线性卡尔曼滤波器进行跟踪。

对车辆行驶环境中的多个车辆目标进行跟踪，需要为每个目标建立一个卡尔曼跟踪器。对当前帧数据进行目标识别后，用识别出的目标更新对应的卡尔曼跟踪器。使用错误的目标更新卡尔曼跟踪器会产生错误的状态估计，造成跟踪失败。因此，在当前帧数据中的目标和卡尔曼跟踪器之间建立正确的关联是多目标跟踪的关键问题。一旦目标关联的问题解决，多目标跟踪也就变成了利用关联到的目标更新多个卡尔曼跟踪器的问题。

2.1 对单个目标的跟踪

利用线性卡尔曼滤波器对目标状态进行估计，目标车辆的状态向量xk包括目标在x方向和y方向的位置和速度，测量向量zk为目标在x方向和y方向的位置，分别为

xk={x0kvxky0kvyk}T

(3)

zk={x0ky0k}T

(4)

运动模型的转换矩阵A为

(5)

式中Δt为传感器采集一帧数据所用的时间。

测量矩阵H为

(6)

过程噪声的协方差矩阵Q为

(7)

式中σp为所加过程噪声。

测量噪声的协方差矩阵为

(8)

式中σm为所加测量噪声的大小。

过程噪声协方差Q和测量噪声协方差R的确定是建立运动模型中的难点。可以通过事先测量一些比较稳定的目标，求出测量误差，得到测量噪声协方差R。但很难对要进行估计的过程进行测量，过程噪声协方差Q一般不容易直接得出。须充分考虑估计的过程中可能产生的误差，使估计过程不会因给定的误差过小而失败。但当考虑的误差过大时，有可能估计的过程本身就不准确。二者在初步确定后，均须根据程序运行后的情况进行离线调整，以使跟踪系统达到最好的性能。

图4为对一辆与本车相向行驶的车辆跟踪的结果。可以看出，有较少的时刻没有检测到被跟踪的目标车辆，在这种情况下，卡尔曼滤波器仍以当前的状态对其进行预测，保持了在遮挡、漏检情况下跟踪的连贯性。图4(b)中y方向的距离在第5～7s之间出现了很大的噪声干扰，卡尔曼滤波大大降低了噪声干扰。

2.2 目标关联

本文中采用确定性方法进行多目标间的关联，以1.2节中提取的目标特征作为约束条件，计算当前帧中检测出的新目标和被跟踪目标的代价函数[3]，根据代价函数的值确定新目标和被跟踪目标间的对应关系。

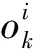
V(i,j)=α×p(i,j)+β×n(i,j)+γ×s(i,j)+κ×r(i,j)

(9)

式中：p、n、s、r分别为1.2节中提取的目标的位置、形状、大小和长宽比；α、β、γ、κ为4个特征的权重值，α+β+γ+κ=1，在对车辆目标的跟踪中，目标位置是最重要的特征，因此权重取值最大，设为0.5～0.7之间。

(10)

(11)

(12)

(13)

2.3 跟踪器的建立和删除

周围环境是不断变化的，出现在检测范围内的目标数目也是变化的。当识别出新的车辆目标时，跟踪算法应能够及时为其建立新的跟踪器，当被跟踪的某个目标消失在检测范围内时，跟踪算法应能够删除对应的跟踪器。这是衡量跟踪算法性能的重要指标。

当传感器开始扫描，或在环境感知的过程中出现新目标时，先将该目标记为新目标，为防止虚警，如果在下一帧数据中仍然出现，才为其建立跟踪器。

在跟踪的过程中，如果某个跟踪器没有与当前帧中的目标产生关联，认为该目标暂时丢失。目标丢失可能是由于遮挡或漏检，也可能是由于目标确实在检测范围内消失。因此，当跟踪器在连续10帧数据中都没有关联到目标时，才认为目标确实消失，将跟踪器删除。如果没有关联到目标的帧数小于10，则继续保留该跟踪器，以跟踪器位置的预测值作为测量值，更新并预测目标的状态，在下一帧数据中继续与识别出来的车辆目标进行关联。

3 实验论证

为验证本文中所述的车辆识别和跟踪算法的有效性，以智能车辆BJUT-IV配备SICK LMS291激光雷达为实验平台，在北京工业大学校内道路上进行数据采集。采用激光雷达采集周围环境的深度信息。采用配备4G内存，酷睿i3处理器的笔记本电脑对数据进行处理，每帧数据的平均处理时间约为20ms。目标识别实验显示，在较理想的状况下，能够准确地识别车辆，但本车的振动、车辆之间的遮挡都会造成目标漏检。当本车靠边行驶时，路边出现类似矩形的障碍物会造成错检。

图5为对前方两个车辆目标连续跟踪的结果，其中图5(a)为第87帧的跟踪结果，图5(b)为第130帧的跟踪结果，由于篇幅限制，省略了中间的跟踪结果。图中，细线框为对目标识别的结果，粗线框为跟踪算法对目标车辆在当前帧中位置的估计值，图左上角显示了所采集到的数据帧数，图5(c)为利用摄像头同步拍摄的场景。图6为对某一车辆目标的跟踪过程。由图6(a)可见，在第282帧，识别出的车辆目标被跟踪。由图6(b)可见，在283～285帧中，由于本车经过减速带产生较大的震动，没有检测到目标，但仍然保留了跟踪器并继续预测。由图6(c)可见，在286帧重新检测到目标，恢复正常的跟踪状态。

4 结论

提出了一种基于深度信息的车辆识别和跟踪算法，可以准确地识别道路上的车辆目标，并对数量不

确定的多目标进行跟踪。采用基于距离的方法对深度信息进行聚类，距离阈值可随目标与本车的远近和相对方位变化而改变，提高了聚类分析的准确性，为后续的特征提取奠定了良好的基础。采用IEPF算法在聚类内部直接提取直线或连续的折线，更加符合车辆目标的特点。在此基础上提取目标特征，利用多特征融合的方式识别车辆目标。利用卡尔曼滤波器对每个目标进行跟踪。多目标间的关联通过计算代价函数实现，代价函数以目标的位置为主要约束条件，计算量小，关联结果准确。

[1] 甘志梅,王春香,杨明.基于激光雷达的车辆跟踪与识别方法[J].上海交通大学学报,2009,43(6):923-926.

[2] Borges G, Aldon M. Line Extraction in 2D Range Images for Mobile Robotics[J]. Journal of Intelligent and Robotic Systems,2004,40:267-297.

[3] Yilmaz A, Javed O, Shah M. Object Tracking:A Survey[J]. ACM Computing Surveys,2006,38(4).

[4] Veenman C, Reinders M, Backer E. Resolving Motion Correspondence for Densely Moving Points[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(1):54-72.

[5] Reid D. An Algorithm for Tracking Multiple Targets[J]. IEEE Transactions on Automatic Control,1979,24(6):843-854.

[6] Ramer U. An Iterative Procedure for the Polygonal Approximation of Plane Curves[J]. Computer Graphics and Image Processing,1972,1(3):244-256.

[7] Douglas D, Peucker T. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer,1973,10(2):112-122.