机电复合传动最优功率分配策略研究*

张东好,韩立金,2,项昌乐,2,王伟达,2

(1.北京理工大学机械与车辆学院,北京 100081； 2.车辆传动重点实验室,北京 100081)

前言

机电复合传动通过电力和机械两路功率流来传递动力，不仅能大幅提高车辆的动力性和燃油经济性，还可以满足大功率用电设备的电能需求，特别适用于重型车辆[1]。功率分配策略是指根据驱动功率需求和用电功率需求，合理地分配电力传动和机械传动的功率，从而提高车辆的动力性和燃油经济性等。可见，功率分配策略是机电复合传动的核心技术，其控制效果直接决定了整车的综合性能。

目前的功率分配策略主要有两大类：基于规则的方法和基于优化的方法[2-3]。前者通过制定规则库来得到各部件的工作状态[4-6]，计算量小，实时性较好，但控制效果较差；后者通过求解优化模型得到各部件的工作状态[7-8]，能够得到最优或近似最优的控制效果，但计算量非常大，无法应用于实时的控制过程。为此，可以借助计算机仿真平台，基于优化的方法得到最优控制轨线，再利用仿真结果指导实时控制规则的制定，并为控制参数的优化提供依据。

本文中基于上述思想，研究了机电复合传动的最优功率分配策略。首先，分析了机电复合传动的多功率流特性，建立了其功率平衡方程；其次，基于上述功率平衡方程提出了最优功率分配策略，并建立了多目标优化模型；然后，提出了动态预测方法，并利用动态规划算法求解了优化模型；最后，对仿真结果进行了分析，验证了最优功率分配策略的有效性和使用价值。

1 机电复合传动特性分析

图1为机电复合传动结构示意图。其中，功率耦合机构由若干行星排和操纵元件组成，用于实现机械功率的分流和汇流。功率分配单元由若干电力电子元件组成，用于实现电力功率的分流和汇流。

可见，机电复合传动是一种多流传动方式。由于多路功率流的存在，在功率需求给定的条件下发动机可以运行在不同的状态，这就带来了最优控制的问题。此外，电机状态的变化也会引起发动机状态的改变，必须同时调节发动机和两个电机，从而带来了协调控制的问题。由于驱动功率和用电功率需求是实时变化的，不同的功率需求下发动机和两个电机的最佳状态也不同，必须根据行驶工况和用电工况实时计算发动机和电机的最优控制指令，并对它们进行动态协调。

功率耦合机构的功率平衡关系为

(1)

式中：Pe、PA、PB分别为发动机、电机A和电机B的功率；ηec、ηAc、ηBc分别为各元件到功率耦合机构的传动效率；Pd为驱动功率，即机电复合传动系统的输出功率；ηcd为功率耦合机构到驱动轮的传动效率；sgn为符号函数。

式(1)中假设电机处于电动状态时其功率为正值，则发电状态下功率为负值，此时功率流的方向发生了改变，因此对其传动效率采用符号函数。同理，由于正常驱动时Pd为正值，则制动能量回收过程Pd为负值，此时功率流的方向发生变化，故对其传动效率也采用符号函数。

车辆的驱动功率需求由两部分组成，一部分用于克服行驶阻力，另一部分用于车辆的加速。车辆驱动功率需求的计算公式为

(2)

式中：Pf为阻力功率；Pm为惯性功率；f为滚动阻力系数；m为车辆总质量；g为重力加速度；v为车速；Cd为风阻系数；A为迎风面积；ρ为空气密度。

可见，式(2)中考虑了整车的动态过程，可用于各种行驶工况。此外，如果给出车辆的行驶工况，利用式(2)就可得到其驱动功率需求。

功率分配单元的功率平衡关系为

(3)

式中：Pb为电池组的功率，充电状态为正值；Pc为用电功率需求，由用电工况得到；ηA、ηB为电机的效率，即机械功率和电功率的转化效率。

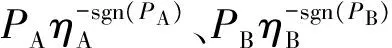
式(3)中假设电池组充电时功率为正值，利用内阻模型可以得到其功率为

(4)

式中：Voc为开路电压；Rb为内阻；Ib为电流。

电池组的荷电状态(SOC)可由下式计算得到：

(5)

式中：t为时间；S为电池组的SOC；Cb为电池组的容量；S0为初始时刻的SOC。

可见，电池组的SOC是时间的函数，不能仅由当前的状态变量计算得到，必须给出电池组在任意时刻的功率Pb(t)。为确定电池组实时的SOC，须进行动态预测，后文中将具体介绍。

2 最优功率分配策略

机械功率平衡方程式(1)和电力功率平衡方程式(3)体现了驱动功率和用电功率需求与各元件功率间的关系。本文中采用基于优化的功率分配策略，即根据上述功率需求最优地分配各元件功率，以实现最佳的综合性能。

最优功率分配策略的基本原则为

(1) 任意时刻的驱动功率需求和用电功率需求得到最大程度的满足；(2)各元件必须在其工作范围内，且满足其自身的动态响应特性；(3)循环工况结束时动力电池组的荷电状态(SOC)恢复到其初始状态；(4)在满足上述原则的前提下，实现机电复合传动系统的综合性能最佳。

可见，最优功率分配策略的核心在于优化模型的建立和求解。其流程图如图2所示，具体步骤如下：首先，根据用电工况、行驶工况和各元件状态计算用电功率需求、驱动功率需求和实时的功率能力，代入电力功率平衡方程和机械功率平衡方程得到各元件的工作范围；然后，选择优化变量并在其约束范围内进行搜索，进而计算各状态变量，并判断是否满足约束条件；最后，计算所有可行状态下机电复合传动系统的综合性能，并找出性能最优的状态集合，从而得到各元件的最优控制命令。

2.1 多元优化目标

机电复合传动系统的功率分配策略不仅影响车辆的动力性、燃油经济性和排放性能，还会影响系统的传动效率、发电能力和电池组的使用寿命等。机电复合传动的最优功率分配是一个多目标优化问题，须综合考虑多方面的性能指标以建立多元优化目标如下。

(1) 发电能力 本文中的重型车辆用电机来实现转向功能，而车辆转向直接决定其安全性，所以须实时满足转向电机的用电功率需求。本文中以用电功率需求和实际发电功率的差值最小为优化目标。

(2) 驱动能力 由于重型车辆对动力性的要求较高，本文中在满足发电能力的前提下，优先考虑驱动能力。以驱动功率需求和实际驱动功率的差值最小为优化目标。在同时满足了发电能力和驱动能力后，再考虑电池组的寿命和车辆的燃油经济性。

(3) 电池组寿命 重型车辆对电池组功率等级的要求较高，而当前的技术条件下电池组的成本非常高，因此，须尽量提高电池组的使用寿命。以电池组SOC的维持为优化目标，在发动机能够满足功率需求的条件下，尽量减少电池组的充放电。

(4) 燃油经济性 机电复合传动是一种多自由度系统，在满足前面各项性能的前提下，还可以对发动机的工作点进行优化，从而提高车辆的燃油经济性。本文中采用全局优化算法，选择整个循环工况的燃油消耗量最少为优化目标。

(5) 其他性能 发动机的排放性能、传动系统的综合效率等也可作为优化目标。上文中在对发动机的工作点进行优化的同时，也会相应改善其排放性能，并提高系统的综合效率，这里不再单独考虑。

本文中采用数值计算方法，把优化目标写成离散的形式：

(6)

式中：k为多步决策的阶段变量；N为决策总数；x(k)为第k步时各元件的初始状态集合，包括发动机的转速ne(k)、转矩Te(k)，电机A的转速nA(k)、转矩TA(k)，电机B的转速nB(k)、转矩TB(k)及动力电池组的荷电状态S(k)；u(k)为第k步的决策变量，该决策是指决定下一时刻各元件的状态，则有u(k)=x(k+1)。

对于多元化的优化目标，通常采用加权的方法进行处理。由于重型车辆对发电能力和驱动能力要求非常高，为了满足这两方面的性能，须牺牲车辆的燃油经济性和电池组的使用寿命。因此，可以认为发电能力和驱动能力的加权系数为无穷大，此时燃油经济性和电池组的使用寿命可以忽略；只有当实际的发电功率和驱动功率完全等于功率需求的条件下，才对车辆的燃油经济性和电池组的使用寿命进行优化，此时发电能力和驱动能力可以看成是约束条件。

综上所述，根据功率能力与功率需求的对应关系，可把性能函数L写成分段的形式：

(1) 动力性优化

L=α|Pc0(k)-Pc(k)|+|Pd0(k)-Pd(k)|

(7)

式中：Pc0(k)、Pd0(k)分别为第k步的用电功率需求和驱动功率需求；Pc(k)、Pd(k)分别为第k步的实际发电功率和实际驱动功率；α为权重系数，α>1表示优先满足用电功率需求。

式(7)中忽略了车辆的燃油经济性和电池组的使用寿命，仅考虑发电能力和驱动能力，两者可以看成是综合性的动力性指标。

(2) 经济性优化

L=mf(k)+β[S(k)-S0]2

(8)

式中：mf(k)为第k步的燃油消耗量；β为惩罚系数，β越大表示对SOC的变化越敏感。

式(8)中不包含发电能力和驱动能力，这是因为实际的发电功率和驱动功率完全等于其功率需求，即其差值为零，因此可以省略。仅考虑车辆的燃油经济性和电池组的使用寿命，两者可以看成是综合性的经济性指标。

2.2 选取优化变量

本文中的最优决策是指根据各元件在任意时刻的初始状态，确定其下一时刻的工作状态，从而获得最佳的综合性能。因此，决策变量本身也是一种状态变量。而机电复合传动系统中各元件的工作状态存在一定的联系，只须给定个别元件的工作状态就可确定其他元件的状态，因此，只须选择部分状态变量作为决策变量进行优化计算，称之为优化变量。

由于优化目标采用了分段的形式，为了便于计算，根据优化目标的变化选择不同的优化变量。如果进行动力性优化，则选择两个电机的转矩为优化变量；如果进行经济性优化，则选择发动机的转速转矩为优化变量。

2.3 约束条件处理

根据最优功率分配策略的基本原则可知，任意时刻各元件都必须在其工作范围内，则有

ne_min≤ne≤ne_max，Te_min(ne)≤Te≤Te_max(ne)；

nA_min≤nA≤nA_max，TA_min(nA)≤TA≤TA_max(nA)；

nB_min≤nB≤nB_max，TB_min(nB)≤TB≤TB_max(nB)；

Smin≤S≤Smax，Pb_min≤Pb≤Pb_max。

由于发动机具有一定的动态响应特性，其工作状态不能阶跃变化，而是需要一个响应时间。图3为发动机的调速特性实验曲线。可见，发动机在调速过程中存在一定的超调和延迟。这里为了简化计算，用升速变化率k+和降速变化率k-来限制发动机转速的动态变化。

表1为发动机调速过程中的动态响应时间和转速变化率，相关数据由图3中的调速特性实验曲线得到。对上述实验数据进行线性拟合，从而得到发动机在不同转速下的升速变化率k+和降速变化率k-，如图4所示。

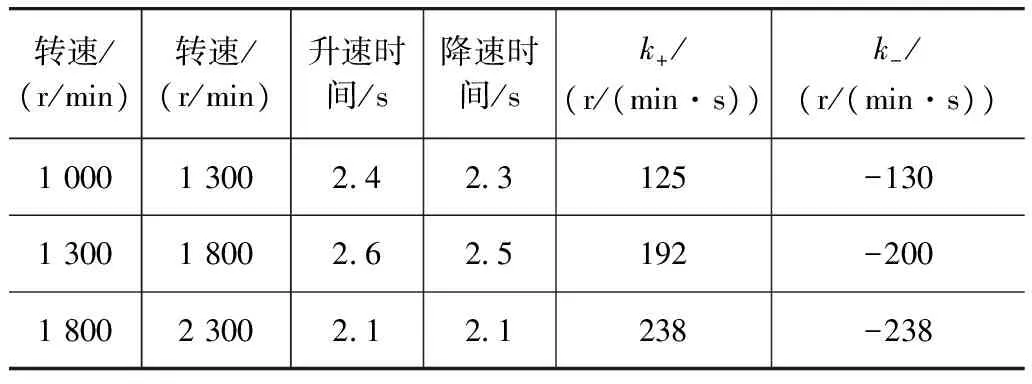
表1 发动机动态响应时间

图4示出了发动机的升速变化率和降速变化率，这两条曲线限制了发动机的转速范围。发动机的转速约束可表示为

ne(k)+Δt·k-≤ne(k+1)≤ne(k)+Δt·k+

式中Δt为仿真步长。

同理，可以对电机的动态响应特性进行类似处理。但是，电机的响应时间为毫秒级，而本文的仿真步长为秒级，可以认为电机的工作状态瞬间达到目标值，即无须限制其动态变化率。

3 动态规划算法

3.1 求解算法

机电复合传动的最优功率分配属于非线性系统在时变约束条件下的多目标优化问题，目前主要有数学规划、进化算法和网络分析等求解方法。由于动态规划特别适用于解决多步骤决策问题，而且能够得到全局最优的控制效果，可以作为其他优化算法的基准[9-10]，因此本文中选择动态规划算法求解上述优化模型。

利用最优性原理，可把式(6)改写为

J(k)=min{L[x(k),u(k),k]+J(k+1)}

(9)

式中J(k)为第k步的优化目标。

利用式(9)可把复杂的多段最优决策问题简化成单一段的最优决策问题，从而大大减小计算量。动态规划算法采用反向递推方法，即从最后一段逐步向前进行优化计算。在进行每一段的最优决策时，不能孤立地只考虑这一段的最优，而是要考虑从这一段开始直到最终的全局最优。针对本文的多目标优化模型，动态规划算法的计算过程如图5所示。

首先，进行最后一段的决策。由于各元件具有唯一的终端状态，则第N步的各节点具有相同的决策，即u(N,i)=x(N+1)。根据第N步的终端状态x(N+1)，判断各初始状态x(N,i)是否满足约束条件，淘汰不可行的节点，并根据初始状态和终端状态计算各可行节点的性能函数L(i)=mf+β[S-S0]2。由于决策变量是唯一的，则各节点的优化目标等于其性能函数。

然后，依次从后向前进行各段决策。以第k步为例进行说明。根据这段的初始状态x(k,i)，找出所有可行的终端状态x(k+1,j)，并判断其是否满足功率需求；对于满足功率需求的决策，性能函数L(i,j)=mf+β[S-S0]2；如果所有决策都不满足功率需求，则性能函数L(i,j)=α|Pc0-Pc|+|Pd0-Pd|，再利用式(9)就可找出最优决策和优化目标。由于式(9)不仅包含了该段的性能函数，还包含了下一段的优化目标，因此能够实现从该段开始直到最终状态的全局最优决策。

最后，进行第1段的决策。由于各元件具有唯一的初始状态，则第1段具有唯一的最优决策。这样就可以根据第1个时间节点各元件的工作状态得到第2个时间节点各元件的最佳状态(唯一状态集合)，再从前向后依次得到每个时间节点各元件的最佳状态。通过把每个时间节点下各元件的工作状态连接起来，就可以得到整个仿真时间(循环工况)内各元件的最优轨线。

3.2 动态预测

上文介绍了多目标优化模型的求解算法。然而，在利用动态规划算法寻找最优轨线之前，必须已知各段决策的初始状态和终端状态，即必须提前获得每个时间节点下所有可能的状态集合。由于发动机和两个电机的工作状态可以由当前的优化变量计算得到，通过对优化变量进行实时搜索就可以得到其状态集合。但是，电池组的SOC是时间的函数，不能仅由当前的优化变量计算得到，它还依赖于前面各阶段的决策。而动态规划采用反向递推方法，在进行每一阶段决策时前面各阶段的决策都是未知的。为了解决这一问题，可以根据上一时刻电池组所有可能的工作状态对其当前的SOC进行预测。

对式(5)的两侧求导，可以得到电池组SOC的微分表达形式为

(10)

式中G(t)为SOC的增量函数。

利用梯形公式，把微分方程(10)表示成离散的形式：

(11)

式(11)是电池组SOC的动态预测方程。根据上一时刻的状态变量和当前的优化变量，利用式(11)就可以得到当前的SOC值。由于该方法可以依次对相邻时刻的SOC进行预测，因此称之为动态预测方法。

由图5可知，1个节点可能对应着多个初始状态，所以该节点的SOC值并不唯一，而是对应着1个约束范围。只要后续的决策满足了该约束范围，就说明该决策可以实现；如果后续的决策超出了该约束范围，则说明该决策无法实现。这样就可以把动态预测和动态规划结合起来，首先通过动态预测方法(正向计算)得到各元件的可行轨线，再通过动态规划方法(反向计算)得到其最优轨线。

3.3 仿真验证

现在对多目标优化模型及其求解算法进行仿真验证，根据给出的行驶工况和用电工况，可利用MATLAB编程得到各元件的最优控制轨线。

图6为本文中采用的行驶工况，它结合了常见的NEDC、EUDC和HWFET等多种循环工况，是一种综合行驶工况。其中，前350s代表了紧急加速和制动工况，后650s代表了任意车速段的匀速工况和各车速段间的加减速工况。

图7为上述行驶工况对应的驱动功率需求，由式(2)计算得到。可见，匀速和缓加速工况下驱动功率主要用于克服行驶阻力，紧急加速工况下驱动功率主要用于克服加速阻力，紧急制动工况下驱动功率为负值，从而实现再生制动。

图8为本文中采用的用电工况。其中，用电功率需求主要包括两部分：一部分来自辅助电机等用电设备，其功率需求是确定值；另一部分来自转向电机等用电设备，其功率需求是随机值。可见，用电功率需求是有限范围内的随机变量。

图9为各元件的最优控制轨线。可见，各元件均在其工作范围内，且其状态的变化比较平稳，这就保证了各元件的动态响应能够实时跟踪其参考轨线，使实际的控制过程具有可行性。

图10为功率需求的跟踪情况。可见，用电功率需求和实际供电功率曲线完全重合，这就在控制算法上保证了发电性能要求。而受到发动机动态响应的限制，部分工况下实际驱动功率未能与驱动功率需求完全重合，但是能够实现非常好的跟踪效果，从而保证了车辆的动力性能。

图11为各元件的功率分配曲线。由于电池组的功率等级较低，由发动机来满足整车的功率需求，而电池组用于补偿发动机的动态响应特性及实现制动能量回收。两个电机主要用于配合发动机实现其工作点的调节，其功率差值用于给用电设备供电并实现电池组SOC的维持。可见，上述功率分配曲线可以用于指导实时功率分配策略的制定，并且为控制参数的优化提供依据。

3.4 实时应用

对于任意给定的行驶工况和用电工况，利用动态预测和动态规划相结合的优化算法，总可以得到发动机和两个电机的最优控制轨线。但是，在实际的控制过程中，行驶工况和用电工况都是未知的。为了解决该问题，可以根据车辆当前的工作状态，估计其未来一段时间内的驱动功率需求和用电功率需求，并在这段时间内进行优化计算。此外，为了提高实时控制算法的计算效率，还可以在离线运算数据的基础上进行多维插值，即根据当前的车速、发动机转速、用电功率需求和驱动功率需求4个输入量插值得到发动机和两个电机的最优控制命令。

这里控制发动机的转速和两个电机的转矩，其最优控制命令为

(12)

(13)

(14)

表2为不同优化算法的运算次数和实时性对比。其中，假设有10个时间节点，每个节点对应10个状态，每个状态运算10次，而局部优化时选择2个节点。可见，穷举搜索算法的计算量最大，实时性非常差；全局动态规划算法的效率大幅提升，但是计算量仍然非常大；局部动态规划算法的计算效率进一步提升，但是仍然难以满足实时控制的要求。而多维插值算法能够极大地减少运算次数，具有非常好的实时性。

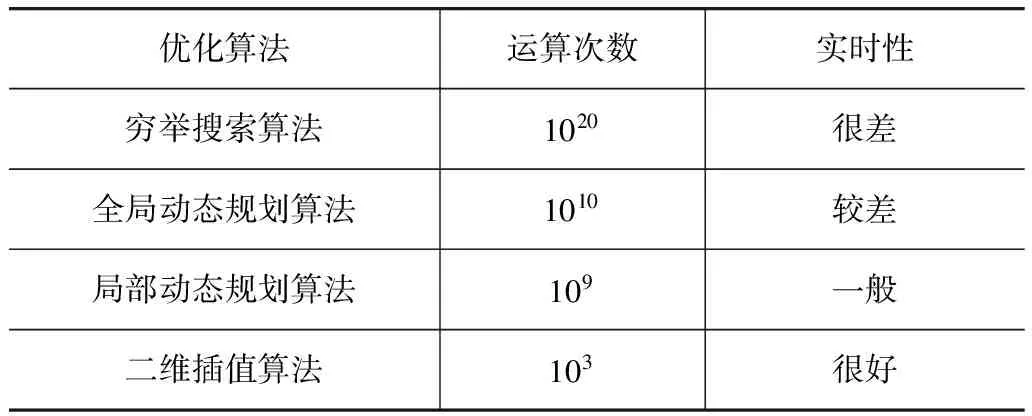
表2 算法的实时性对比分析

4 结论

(1) 基于机电复合传动的多功率流传动特性，建立了机械功率平衡方程和电力功率平衡方程，并给出了动态功率需求的求解方法，为功率分配策略的制定奠定了基础。

(2) 提出了机电复合传动的最优功率分配策略，并建立了多目标优化模型。基于重型车辆的动力性、经济性和用电特性，建立了多元化的优化目标，提取了自适应的优化变量，并对非线性时变的约束条件进行了处理。

(3) 针对本文中的多目标优化模型，提出了动态预测和动态规划相结合的求解算法。基于综合行驶工况和随机用电工况，得到了各元件的最优控制轨线及其功率分配曲线。仿真结果验证了最优功率分配策略的可行性，并为实时功率分配策略的制定和优化提供了依据。

[1] 王伟达,项昌乐,韩立金,等.机电复合传动系统综合控制策略[J].机械工程学报,2011,47(20):152-158.

[2] Salmasi Farzad R. Control Strategies for Hybrid Electric Vehicles:Evolution, Classification, Comparison, and Future Trends[J]. Vehicular Technology, IEEE Transactions on,2007,56(5):2393-2404.

[3] Gurkaynak Y, Khaligh A, Emadi A. State of the Art Power Management Algorithms for Hybrid Electric Vehicles[C]. IEEE Vehicle Power and Propulsion Conference,2009:388-394.

[4] 王伟达,项昌乐,韩立金,等.基于电池SOC保持的混联式混合动力车辆能量管理策略的研究[J].汽车工程,2011,33(5):373-377.

[5] Jalil N, Kheir N A, Salman M. A Rule-based Energy Management Strategy for a Series Hybrid Vehicle[C]. American Control Conference,1997:689-693.

[6] Ganji B, Kouzani Z, Khayyam H. Look-ahead Intelligent Energy Management of a Parallel Hybrid Electric Vehicle[C]. Fuzzy Systems(FUZZ),2011 IEEE International Conference on,2011:2335-2341.

[7] Zanasi R, Grossi F. Modeling and Control of Power-split Hybrid Electric Vehicles[C]. Vehicle Power and Propulsion Conference (VPPC),2010 IEEE,2010:1-6.

[8] Opila D F, Aswani D, McGee R, et al. Incorporating Drivability Metrics into Optimal Energy Management Strategies for Hybrid Vehicles[C]. Decision and Control,2008. CDC 2008. 47th IEEE Conference on,2008:4382-4389.

[9] Liu Jinming, Peng Huei. Control Optimization for a Power-split Hybrid Vehicle[C]. American Control Conference,2006:466-471.

[10] Wang Wei, Liu Xinhui. Optimization and Simulation of Energy Management Strategy for a Parallel-series HEV[C]. International Conference on Computer Application and System Modeling,2010:488-492.