四边手性蜂窝动态压溃行为的数值模拟＊

卢子兴，李 康

（北京航空航天大学固体力学研究所，北京100191）

与普通多孔材料相比，拉胀多孔材料具有更高的冲击阻抗、抗剪能力、抗凹能力和能量吸收能力，在航空航天领域中有着广泛的应用前景，如用作结构防护材料和夹层板芯层材料等［1－5］。在现有材料的基础上，寻找能量吸收效率更高的材料，并对现有的吸能材料和结构进行优化设计和改进，已经成为当今力学界和材料学界的一个研究热点［6－8］。早在1996 年，D.Prall等［9］就对二维的六边形手性蜂窝（hexachiral）的面内力学行为进行了理论分析和实验研究。后来，A.Alderson等［10］对具有手性构型的一系列蜂窝在面内准静态压缩下的力学行为进行了实验研究，给出了压缩应变为1%或2%时的应力应变关系曲线，得到了面内弹性模量和泊松比，并进行了有限元模拟与实验的对比。最近，A.Spadoni等［11］采用微极连续介质模型来描述拉胀手性蜂窝，试图消除由泊松比为－1引起的本构关系的不确定性。F.Dos Reis等［12借助渐进均匀化方法对5种二维周期性拉胀蜂窝进行了分析，得到了模量和泊松比的封闭解，认为导致负泊松比的2种主要机制是内凹机制和旋转机制。目前，仍有一些新型拉胀拓扑结构在不断涌现［5，13－14］，寻找更高负泊松比的蜂窝拓扑结构已成为该领域的主题之一。拉胀蜂窝是一种新型多孔材料。要在结构上广泛使用拉胀蜂窝，首先需要对其力学性能有充分的研究和认识。当前的研究工作主要集中于发现新的拉胀蜂窝拓扑结构和预测其准静态力学性能及解释负泊松比变形机制上，然而，实际应用中对其用作夹层结构或能量吸收构件材料时，遭受外来物冲击的动态行为尚缺乏了解，因此，对于拉胀蜂窝结构在冲击载荷作用下的动力学性能展开研究就显得尤为必要，而目前对此还未见报到。

本文中，采用数值模拟方法，对四边手性蜂窝在不同冲击速度下的变形模式和能量吸收等动力学响应特性展开研究，以确定这种蜂窝在不同冲击速度下的变形模式和能量吸收性能，并同普通六边形蜂窝的冲击行为进行对比，以期为进一步研究三维拉胀泡沫材料的动态冲击行为奠定基础。

1 模型的建立

1.1 手性蜂窝的几何结构

四边手性蜂窝（tetrachiral）是具有四边手性构型的拉胀蜂窝结构材料。图1给出了四边手性蜂窝的几何结构参数，其中，l、r、δ 分别为支柱的长度、圆形节点的半径及壁厚，支柱和圆形节点的壁厚相同。所 有 算 例 中 取l ＝20 mm，δ ＝1.5 mm，r＝5mm。

1.2 有限元模型

采用ANSYS／LS－DYNA 显式动力分析有限元软件对手性蜂窝面内冲击特性进行数值分析。计算中，基体材料选用金属铝，假定为理想弹塑性材料，材料参数分别为：弹性模量Es＝69GPa，屈服应力σys＝76MPa，密 度ρs ＝2 700 kg／m3，泊 松 比νs＝0.3。胞壁选用SHELL163壳单元，壳单元的平均长度为2mm，支柱单元数为10，圆形节点单元数为16。采用全积分Belytschko－Tasy 壳单元算法，为了收敛性需要，沿厚度方向定义5个积分点。另外，蜂窝模型采用单面自动接触算法进行计算，刚性板表面与蜂窝试件的外表面采用面－面接触算法，摩擦因数取为0.25。图2为蜂窝材料的有限元模型。

图1 四边手性蜂窝单元Fig.1 Diagram of tetrachiral cell

如图2（a）所示，模型在2 个方向上均采用10 个胞体单元，整个蜂窝模型的长、宽尺寸均取为211.2mm。蜂窝模型放置在上、下2个刚性板中间，计算过程中将下刚性板固定，上刚性板以某一初速度向下冲击蜂窝模型，冲击速度范围取为3.5～140m／s。计算中限制整个蜂窝模型所有节点的面外位移，以保证平面应变状态。

为了与普通六边形蜂窝材料的冲击力学性能进行比较，也为了验证计算模型的有效性，选取D.Ruan等［15］所采用的六边形蜂窝模型（与手性蜂窝相对密度一致）作为对比模型，如图2（b）所示。正六边形蜂窝的边长l′＝2.7mm，壁厚δ′＝0.5mm，水平方向取16个胞体单元，竖直方向取19个胞体单元，整个蜂窝模型的长和宽分别为74.8和78.3mm。需指出，在D.Ruan等［15］的分析中蜂窝模型的底面是固定的，而在本文的分析中蜂窝模型是放置在固定刚性板上的。

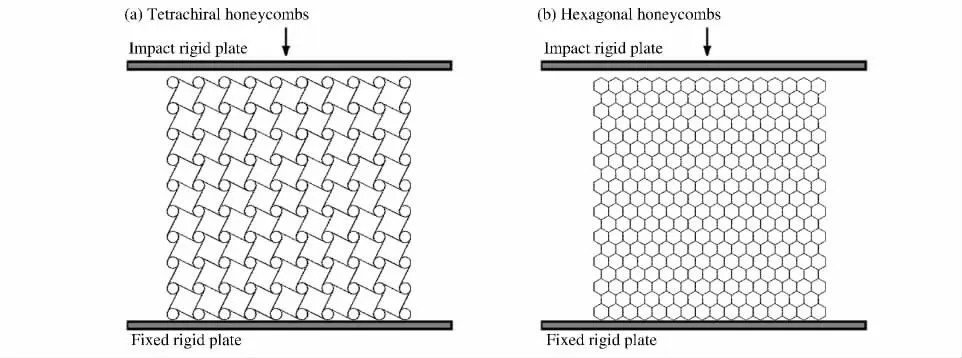
图2 蜂窝材料的有限元模型Fig.2 FE models of honeycombs

2 模拟结果和讨论

2.1 普通六边形蜂窝的变形模式

图3～4给出了不同速度冲击下普通六边形蜂窝（hexagonal）的变形模式，其中的ε 为蜂窝的名义压缩应变，即蜂窝顶面的压缩位移与模型初始高度之比。当刚性板的冲击速度为7.0m／s时，首先在蜂窝模型的中上部形成局部变形带，呈“V”形，这与文献［15］中所展现的变形模式一致；随着压缩的进行，在固定端也形成了不太明显的倒“V”形剪切带，局部变形带的进一步扩展使蜂窝模型被逐渐压溃。当刚性板的冲击速度为70.0m／s时，蜂窝的变形模式发生了显著变化，局部变形集中于冲击端。随着压缩量增加，蜂窝胞元被逐层压溃，局部变形带表现为“I”形，自冲击端至固定端，蜂窝被压缩密实。

图3 冲击速度为7.0m／s时六边形蜂窝的变形模式Fig.3 Deformation modes of hexagonal honeycombs under the impact velocity of 7.0m／s

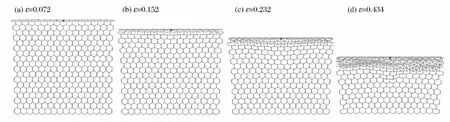
图4 冲击速度为70.0m／s时六边形蜂窝的变形模式Fig.4 Deformation modes of hexagonal honeycombs under the impact velocity of 70.0m／s

综上所述，在低速冲击下，六边形蜂窝压溃变形模式为“V”形坍塌带，而高速冲击时压溃变形模式为“I”形坍塌带，这在D.Ruan等［15］的工作中已有详细说明，仅由于边界条件不同而带来细微的差异，在此不再赘述。

2.2 四边手性蜂窝的变形模式

四边手性蜂窝在面内不同冲击速度下的变形模式与六边形蜂窝的面内动态压溃变形模式有较大的区别，图5～7分别给出了低速、中速和高速冲击下四边手性蜂窝的变形历程。

当冲击速度为3.5m／s时，在刚性板的压缩下，固定端附近竖直方向的斜支柱首先产生弯曲变形，自左向右逐渐传播开来。紧接着冲击端附近的斜支柱也遵循同样的模式产生变形，只不过是自右向左。由此产生了2个较显著的局部剪切变形带。进而，支柱卷绕在圆形节点上，圆形孔壁发生了初步的堆积，两端的局部变形带同时向内部扩展，模型的中部产生了明显的转动。支柱的卷绕与张开正是手性蜂窝产生负泊松比行为的变形机制［9］。由图5（c）可以看到模型在垂直于加载方向上产生了收缩，可形象地称之为“缩颈”现象。此时，圆形节点已充分接触，然后变形开始集中在圆形孔壁上，随着圆形孔壁的坍塌，模型进一步压溃，材料充分接触，进入到密实化阶段。上述模拟结果表明，手性蜂窝在低速冲击下的变形大致可分为2个阶段，第1阶段为支柱的弯曲卷绕和圆形节点的转动，第2阶段为圆形孔壁的坍塌。在低速冲击下，手性蜂窝的变形模式可归结为“Z”字形模式。

当冲击速度升高到56.0m／s时，固定端的局部变形带的形成已明显滞后于冲击端，惯性效应明显地表现出来。刚性板与蜂窝模型开始接触时，只在冲击端附近产生了局部变形，并且变形不同于低速冲击时的情形，而是以靠近冲击端的圆形孔壁的坍塌为主，伴随着第1排竖直斜支柱的少量弯曲变形。随着加载位移的增加，靠近冲击端一侧的胞体单元进一步坍塌，此时已观察不到模型中部的整体转动，只产生不太明显的“缩颈”。在远离冲击端的位置，变形仍以支柱的弯曲卷绕和圆形节点的转动为主。紧接着模型下部的圆形孔壁开始大量地坍塌，直至整个模型被完全压实。

当冲击速度为140.0m／s时，惯性效应进一步增强，手性蜂窝在该冲击速度下已表现为与普通蜂窝材料一致的典型高速冲击下的“I”字形变形模式。变形直接表现为孔壁的坍塌和折叠，自顶向下，一层一层地向下传播，直至模型的底部。此时，在手性蜂窝中几乎观察不到“缩颈”现象。

综上所述，在高速冲击下，手性蜂窝的变形表现为从冲击端开始的圆形孔壁与支柱的交替压溃，最终表现为“I”字形变形模式；而在中等速度冲击下，变形模式表现为介于低速变形和高速变形模式之间，为兼有两者部分特征的过渡模式。

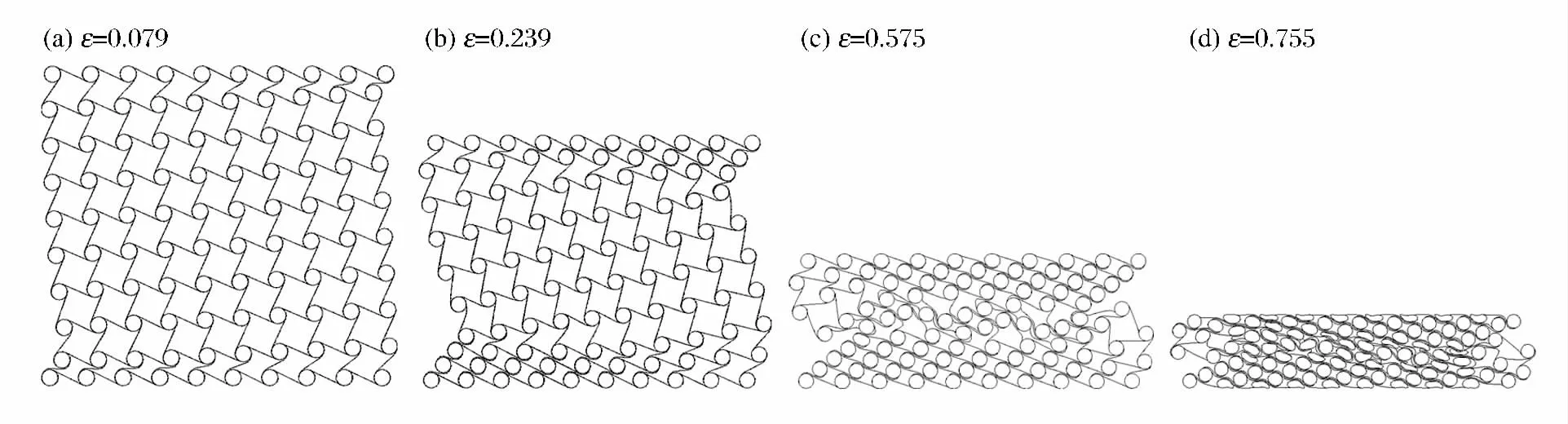
图5 冲击速度为3.5m／s是四边手性蜂窝的变形模式Fig.5 Deformation modes of tetrachiral honeycombs under the impact velocity of 3.5m／s

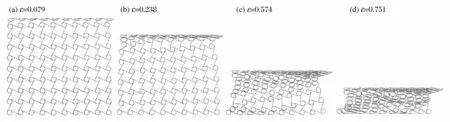
图6 冲击速度为56.0m／s是四边手性蜂窝的变形模式Fig.6 Deformation modes of tetrachiral honeycombs under the impact velocity of 56.0m／s

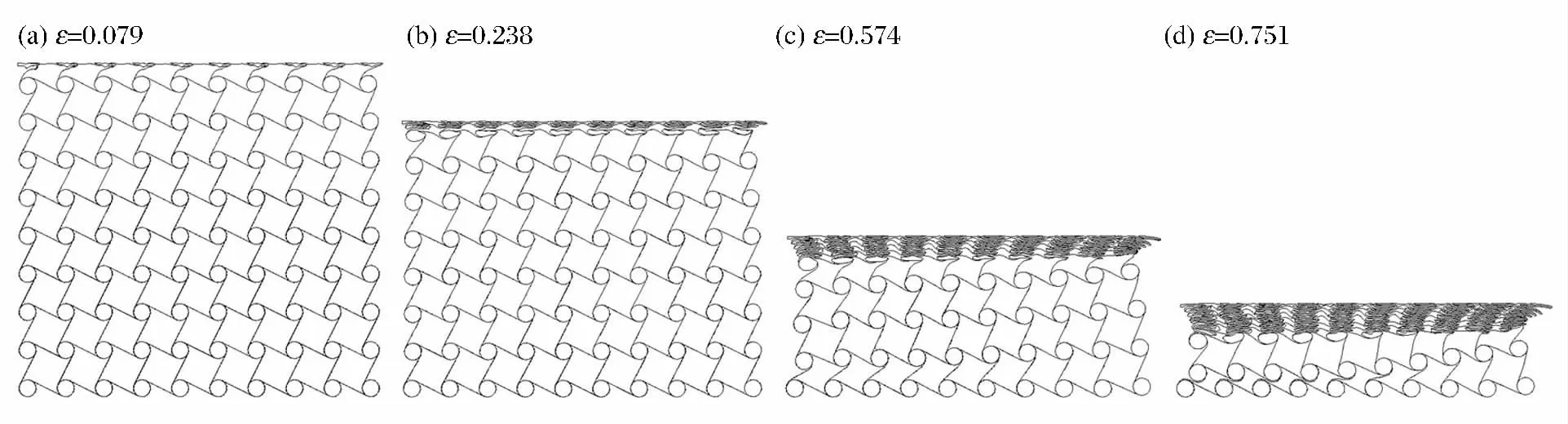
图7 冲击速度为140.0m／s是四边手性蜂窝的变形模式Fig.7 Deformation modes of tetrachiral honeycombs under the impact velocity of 140.0m／s

2.3 不同速度冲击下的动力响应曲线

图8 给出了四边手性蜂窝在不同冲击速度下的压缩反力－位移曲线，图中f 为压缩反力，x 为位移，v 为冲击速度。图8中的曲线揭示了一般多孔材料变形过程中表现出的3个不同阶段［1］。第1阶段为瞬态响应，冲击载荷由零值迅速增加至一个峰值，又突然回落；紧接着是一个较长的坍塌平台区，虽然压缩载荷存在着明显的振荡，但大体上保持不变，平台变形阶段显示了多孔材料压溃时的典型特征，也是能量吸收应用中最关心的变形阶段；随着压缩位移的进一步增加，胞体单元中的孔壁开始接触，变形进入到致密化阶段，到达这个阶段后，压缩位移的微增会导致压缩载荷的陡然上升。

平台区对应的平均冲击载荷可以定义为：

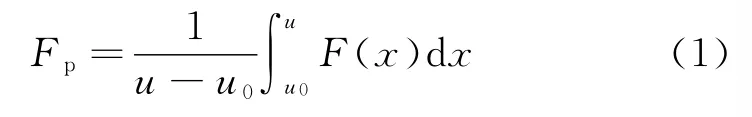
图8 不同速度冲击下四边手性蜂窝结构的压缩反力和压缩位移的变化曲线Fig.8 Dynamic force－displacement curves of tetrachiral honeycombs under different impact velocities

式中：u 为平台阶段蜂窝的顶面位移，u0为冲击载荷达到第1个局部峰值时的位移，F（x）为对应于平台阶段的冲击载荷。通过比较不同冲击速度下手性蜂窝的压缩反力－位移曲线，可以看到，初始冲击载荷峰值、平台区的平均冲击载荷和平台区长度均随着冲击速度的升高而提高。

不同于蜂窝的准静态压缩响应，在冲击过程中，u0通常很小，可近似取为0。这样将蜂窝压缩至某一位移u 时所需要的外力功W（u）可近似为：

该外力功也即冲击过程中冲击刚性板的动能和势能的损失，由蜂窝的变形所吸收，可通过冲击载荷对压缩位移的积分得到。蜂窝吸收的能量E 为：

式中：ud为蜂窝变形进入致密化阶段时所对应的顶面位移。据此可得蜂窝吸收的能量和压缩位移的关系曲线，如图9所示。在整个冲击过程中，蜂窝所吸收的能量大部分由塑性变形耗散掉，部分转化为动能，此外还有一小部分能量通过摩擦阻尼、热能、声能等形式耗散掉。

由式（3）可得单位体积的蜂窝材料压缩到某一应变时所吸收的能量，即：

式中：V 为蜂窝材料的体积。据此可得在相同相对密度但不同冲击速度下单位体积的四边手性蜂窝和正六边形蜂窝吸收的能量与名义压缩应变的关系曲线，如图10所示。

结果表明，对于具有相同相对密度的蜂窝，在蜂窝被压缩到密实化阶段之前，且相对压缩量一致的条件下，不同冲击速度下四边手性蜂窝的能量吸收均低于正六边形蜂窝。

但是，从能量吸收的方式看，手性蜂窝除了胞壁发生塑性变形外，还包含圆形节点的转动。圆形节点的转动能够诱导支柱的弯曲卷绕，使整个蜂窝模型的胞元联动地产生变形，因而能够充分发挥每个胞元的能量吸收作用。可以预见，由圆形节点的旋转产生的转动来吸收一定比例的能量，在手性蜂窝承受中、低速冲击时的能量吸收中具有较大的潜质。通过提高圆形节点的转动动能在手性蜂窝能量吸收中的比例，来提高手性蜂窝的能量吸收能力，是多孔材料能量吸收设计的一个新思路。

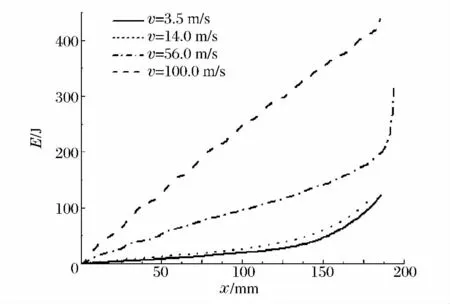
图9 不同速度冲击下四边手性蜂窝结构的能量吸收曲线Fig.9 Energy absorption for tetrachiral honeycombs under different impact velocities

同时，上述计算结果表明，在压缩量一定的情况下，随着冲击速度的提高，所有蜂窝均表现出更强的能量吸收能力。其原因可归结为惯性效应的影响，冲击速度的提高使载荷平台的高度和长度随之增加，同时蜂窝的动能在能量吸收中的比重也显著地增加，蜂窝也就表现出更强的能量吸收能力。

3 结 论

在低速冲击下，四边手性蜂窝的变形大致分为2个阶段：第1阶段为支柱的弯曲卷绕和圆形节点的转动，而第2阶段为圆形孔壁的坍塌，变形模式表现为“Z”字形；在高速冲击下，其变形模式表现为从冲击端开始的圆形孔壁与支柱的交替压溃，这与普通蜂窝的“I”字形变形模式类似；在中等速度冲击下，其变形模式介于低速变形模式和高速变形模式之间，为兼有两者部分特征的过渡模式；在中、低速度冲击时，能够观察到拉胀材料在压缩时特有的“缩颈”现象。随着冲击速度由低到高，局部变形区由固定端逐渐发展到冲击端。此外，计算结果还表明，与六边形蜂窝一样，随着冲击速度的提高，手性蜂窝的能量吸收能力也变强。

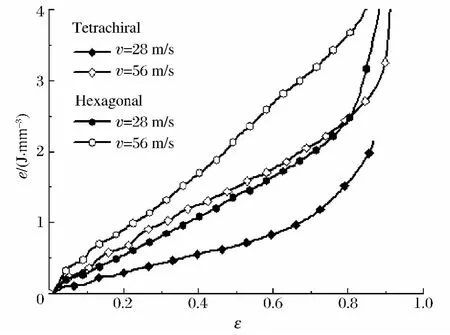
图10 单位体积的四边手性蜂窝结构与正六边形蜂窝的能量吸收能力Fig.10 Energy absorption per unit volume for tetrachiral and hexagonal honeycombs

［1］ Gibson L J，Ashby M F.Cellular solids：Structure and properties［M］.2nd ed.Cambridge：Cambridge University Press，1997.

［2］ Liu Q.Literature review：Materials with negative poisson's ratios and potential applications to aerospace and defence［R］.Victoria，Australia：Defence Science and Technology Organisation，2006.

［3］ Alderson A，Alderson K L.Auxetic materials［J］.Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2007，221：565－575.

［4］ 卢子兴，刘强，杨振宇.拉胀泡沫材料力学性能［J］.宇航材料工艺，2010（1）：7－13.Lu Zi－xing，Liu Qiang，Yang Zhen－yu.Mechanical properties of auxetic foams［J］.Aerospace Materials ＆Technology，2010（1）：7－13.

［5］ Prawoto Y.Seeing auxetic materials from the mechanics point of view：A structural review on the negative Poisson's ratio［J］.Composites Science and Technology，2012，58：140－153.

［6］ 卢子兴，郭宇.金属泡沫材料力学行为的研究概述［J］.北京航空航天大学学报，2003，29（11）：978－983.Lu Zi－xing，Guo Yu.Brief review of studies on the mechanical behavior of metallic foams［J］.Journal of Beijing University of Aeronautics and Astronautics，2003，29（11）：978－983.

［7］ 刘颖，何章权，吴鹤翔，等.分层递变梯度蜂窝材料的面内冲击性能［J］.爆炸与冲击，2011，31（3）：225－231.Liu Ying，He Zhang－quan，Wu He－xiang，et al.In－plane dynamic crushing of functionally layered metal honeycombs［J］.Explosion and Shock Waves，2011，31（3）：225－231.

［8］ Amin A，Hamid N H，Ashkan V.Dynamic crushing and energy absorption of regular，irregular and functionally graded cellular structures［J］.International Journal of Solids and Structures，2011，48（3／4）：506－516.

［9］ Prall D，Lakes R S.Properties of a chiral honeycomb with a Poisson’s ratio of－1［J］.International Journal of Mechanical and Science，1996，39（3）：305－314.

［10］ Alderson A，Alderson K L，Attard D，et al.Elastic constants of 3－，4－and 6－connected chiral and antichiral honeycombs subject to uniaxial in－plane loading［J］.Composites Science and Technology，2010，70（7）：1042－1048.

［11］ Spadoni A，Ruzzene M.Elasto－static micropolar behavior of a chiral auxetic lattice［J］.Journal of the Mechanics and Physics of Solids，2012，60（1）：156－171.

［12］ Dos Reis F，Ganghoffer J F.Equivalent mechanical properties of auxetic lattices from discrete homogenization［J］.Computational Materials Science，2012，51（1）：314－321.

［13］ Dirrenberger J，Forest S，Jeulin D，et al.Homogenization of periodic auxetic materials［J］.Procedia Engineering，2011，10：1847－1852.

［14］ 卢子兴，赵亚斌.一种有负泊松比效应的二维多胞材料力学模型［J］.北京航空航天大学学报，2006，32（5）：594－597.Lu Zi－xing，Zhao Ya－bin.Mechanical model of two－dimensional cellular materials with negative Poisson’s ratio［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（5）：594－597.

［15］ Ruan D，Lu G，Wang B，et al.In－plane dynamic crushing of honeycombs：A finite element study［J］.International Journal of Impact Engineering，2003，28（2）：161－182.