二维热传导方程的紧ADI法

王洁

（台州学院 数学与信息工程学院，浙江 临海 317000）

二维热传导方程的紧ADI法

王洁

（台州学院 数学与信息工程学院，浙江 临海 317000）

对二维热传导方程进行紧交替方向有限差分，该方法在空间方向上具有四阶精度，在时间方向上具有二阶精度.证明了当rx，ry≥1/6时该有限差分解收敛于连续解.数值例子验证了该有限差分法具有高阶精度.

二维热传导方程；紧ADI法；高阶精度；收敛性

1 引言

热传导方程在物理学、生物学中有很重要的作用,已受到广泛关注．工程技术中许多重要问题如微波的热处理、自燃、地下水的传输、扩散物质浓度、电缆的传输等问题都可用热传导方程来描述.

通常用有限差分法求解依赖于时间的热传导方程，如显格式、隐格式及C-R格式.对于高维热传导方程可采用加权差分格式、交替方向显格式、交替方向隐格式（ADI）及局部一维（LOD）法.对于二维热传导方程数值解法出现了许多研究成果,但它们主要进行的是解的存在性与稳定性分析［1］-［4］，很少有收敛性方面的工作.

廖文远等人［5］提出了一种紧交替方向隐式有限差分方法，即在时间方向上用Crank-Nicolson方法近似，在空间方向上用Padé方法逼近．这种方法具有紧的性质，并且在时间方向上具有二阶精度，在空间方向上具有四阶精度．优点是将一个二维问题降为两个一维问题，这将大大降低求解难度．本文利用紧ADI方法对二维热传导方程进行有限差分，并把它写成矩阵的形式,证明了当rx，ry≥1/6时有限差分解收敛于连续解，并给出数值例子验证。

2 紧ADI有限差分格式

考虑如下二维热传导方程：

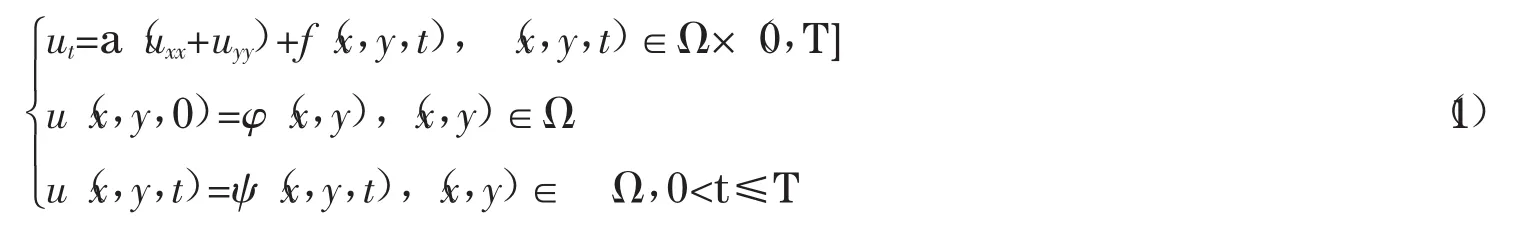
其中Ω=（0，1）×（0，1），u（x，y，t）表示温度，f（x，y，t）为源项，φ和ψ是已知函数，且具有充分的光滑性，a为导温系数或热扩散系数.

将Ω分别在x和y方向上进行分割，步长分别为hx和hy．将（0，T]进行分割，步长为τ．记My=1/hx，My=

1/hy，Mt=T/τ．离散点记作．为方便起见，我们用数对（i，j）表示离散点（xi，yj），记：

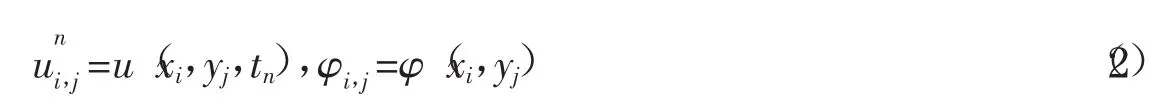
定义标准的中心差商算子：

在时间方向上用Crank-Nicolson格式，在空间方向上用Padé逼近，我们有如下有限差分逼近［5］：

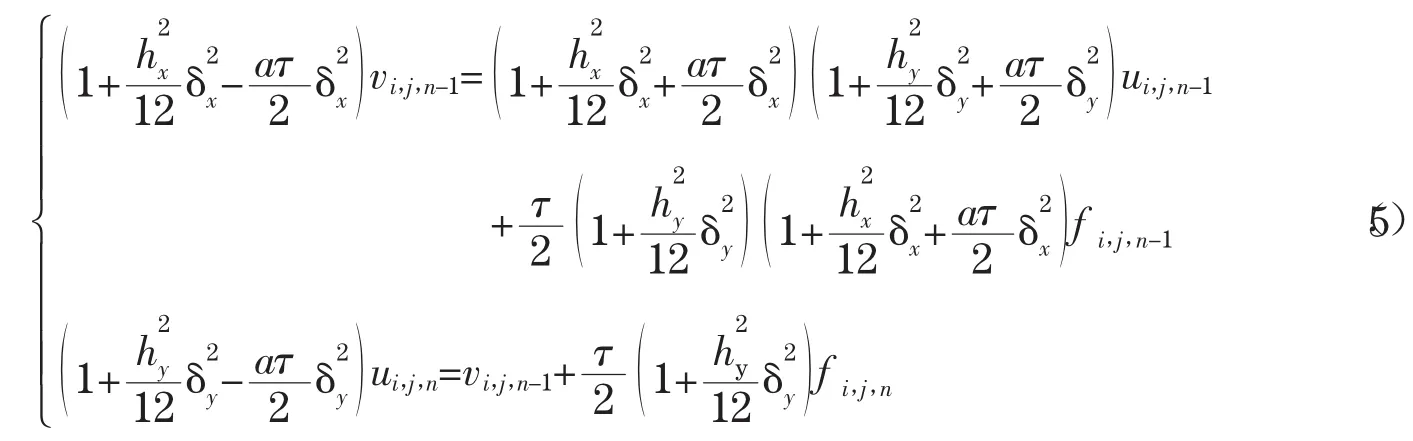
此处，ui，j，n表示在点（xi，yj，tn）处的u逼近．因为（5）左边部分分别只含有三点中心差分算子，所以它将两维问题（4）降低为两个一维问题，故得到一个ADI算法．即第一步是沿x方向利用Thomas算法逐行求解三对角方程，得到vi，j，n-1，然后沿y方向逐列求解三对角方程得到解ui，j，n，由于每步只需求解一组三对角方程，且两个方向交替变换，故通称这类格式为交替方向隐格式.

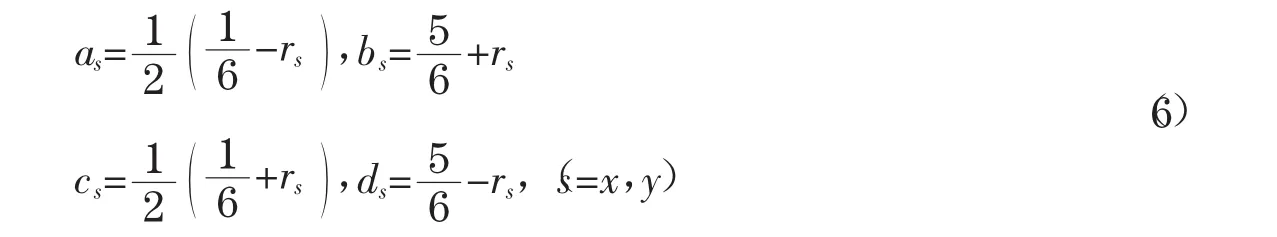
定义如下的列向量：

我们也定义如下（Mx-1）阶的对称三对角矩阵：

和（My-1）阶对称三对角矩阵：

则（5）式可以写成如下矩阵形式：

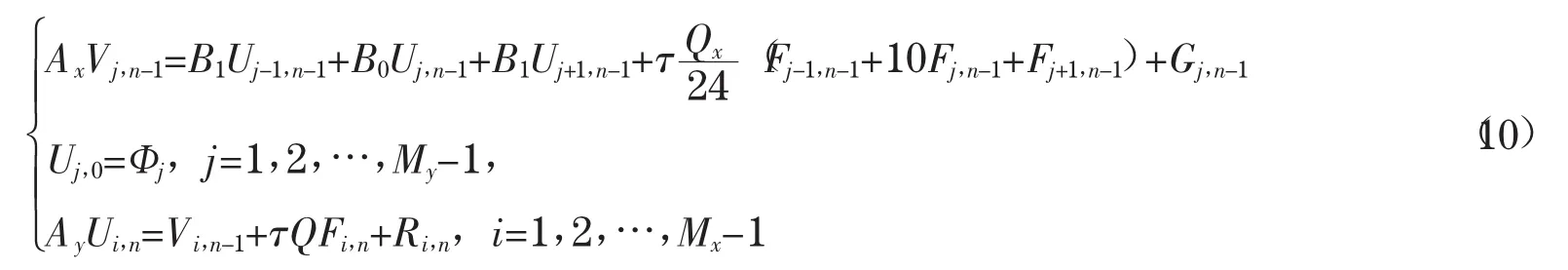
这里对每个n和j，U0=UM，n=0，Gj，n和Ri，n是与边界函数相关的两个向量。

为了将（10）写成更紧凑的形式，定义如下向量：

向量Un和有相同的分量，向量Un是先排x方向，后排y方向，而向量是先排y方向，后排x方向,它们的唯一的区别是分量的次序.

记M=（Mx-1）（My-1），引入以下M阶块矩阵：

于是，（10）可写成

3 收敛性

定理2.1.设Un为方程（1）的精确解，Wn为方程（13）的数值解.当rx，ry≥1/6时，Wn收敛于Un，n=0，1，…，Mt．

这就证明了定理结论．

4 数值例子

下面通过具体数值例子来分析前面格式的收敛性.在0≤x，y≤1内考察精确解为u（x，y，t）=e-2π2tsin （πx）sin（πy）的初边值问题，初始条件由精确解给出.表1给出了当r=1/2时，在（1/2，1/2）点处精确解和紧ADI方法数值解的比较，由此看出，紧ADI方法得到的数值解误差很小，数值解收敛于精确解，收敛阶数是4阶.比［4］中方法得到的误差要小.

表1 r=1/2时的紧ADI法最大误差和收敛阶Tab.1 Maximum error and convergence rate for compact ADI method when r=1/2

［1］叶其孝，李正元.反应扩散引论［M］.北京：科学出版社，1994.

［2］戴嘉尊，邱建贤.微分方程数值解法［M］.南京：东南大学出版社，2002.

［3］张文生.科学计算中的偏微分方程［M］.北京：高等教育出版社，2006.

［4］葛永斌.高维热传导方程的高精度交替方向隐格式［J］.上海理工大学学报,2007,29（1）：56-58.

［5］Wenyuan Liao,Jianping Zhu,and Abdul Q.M.Khaliq.An Efficient High-Order Algorithm for Solving System of Reaction-Diffusion Equations［J］.Numerc Methods Partial Differential Eq,2002,18：340-354.

［6］Yuan-Ming Wang，Jie Wang．A higher-order compact ADI method with monotone iterative procedure for systems of reaction-diffusion equations［J］．Computers and Mathematics with Applications，2011，62：2434-2451．

［7］A.Berman，R.Plemmons，Nonnegative Matrix in the Mathematical Science，Academic Press，New York，1979．

Compact ADI Method for Solving Heat Equation with Two Dimensions

WANG Jie

（School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China）

A high order algorithm is discussed in the paper. This algorithm has the accuracy of four-order in space and two-order in time.The finite difference scheme can be solved by ADI method.The convergence of finite difference solution to the continuous solution is proved when it is between 1/6 and 5/6.A numerical example is shown the high accuracy of the finite difference in the last section.

heat equation with two dimensions;compact ADI method;high order accuracy;convergence

10.13853/j.cnki.issn.1672-3708.2014.03.003

2014-04-17

台州学院青年项目（2013QN09）

王 洁（1982- ），女，浙江仙居人，讲师，硕士，主要从事计算数学研究。