基于MATLAB的圆形线圈磁场强度与线圈个数的线性关系仿真
2014-02-22
(中煤科工集团西安研究院有限公司,陕西西安,710074)
基于MATLAB的圆形线圈磁场强度与线圈个数的线性关系仿真
程 海,宫 浩,陈 坤,王昊星,岳 辉
(中煤科工集团西安研究院有限公司,陕西西安,710074)
MATLAB软件为复杂、抽象物理现象的动态仿真提供了简单、高效的编码环境。文章在利用毕奥——萨伐尔定律推导出圆环电流磁场分布现象的数学模型基础上,运用MATLAB软件对圆形线圈轴线磁场分布进行验证及仿真,得到了圆形线圈轴线磁场强度与线圈个数的线性关系分析结果。
matlab;圆形线圈;磁场分布;磁场叠加
0 前言
毕奥——萨伐尔定律是以实验为基础经过科学抽象而得到的,描述的是电流元在空间任一点产生的磁感应强度。原则上利用毕奥——萨伐尔定律并结合磁感应强度叠加原理,可以计算任意形状的电流所产生的磁场。本文主要讨论圆环电流所产生的磁场分布情况,利用MATLAB软件对不同数量的圆形线圈叠加产所生的磁场进行仿真,最后对结果进行讨论。
1 圆环电流在空间任一点的磁场分布

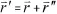
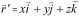
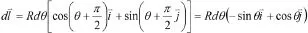
根据圆环电流的电流分布特点,可知在图1中以z轴上某点为圆心、圆面平行于圆环电流的圆周上个点的磁场大小相同,方向表述也应该相同,那么P点的坐标为(x,0,z)的结果页具有就普遍性。因此有:
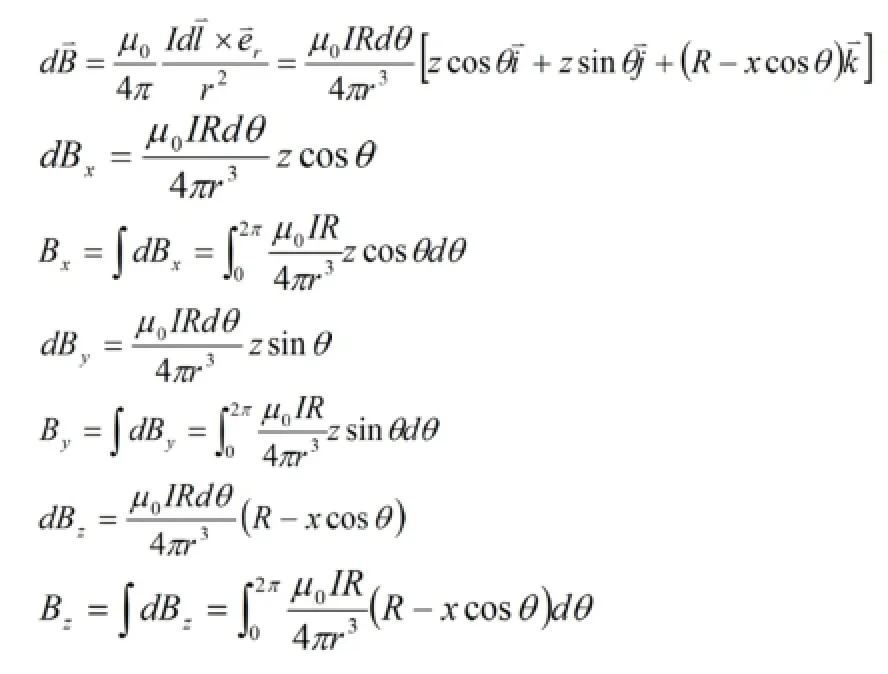
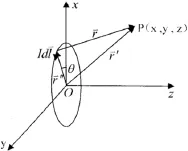
图1 圆环电流磁场分析用图
2 利用MATLAB进行仿真
在利用毕奥——萨伐尔定律对圆环电流磁场进行数学模型分析后,下面利用matlab对不同数量圆形线圈叠加后所产生的磁场情况进行仿真分析。
首先对半径为1 m,线圈个数从1到10依次叠加后产生的磁场进行仿真,仿真标号为Ⅰ,如图2所示,仿真Ⅰ的条件如下:
1)圆形线圈,半径R=1 m;
2)电流I=3 A,理想方波信号输入;
3)磁场强度对比点选取为线圈平面正上方,沿圆心轴线1 m的A点。
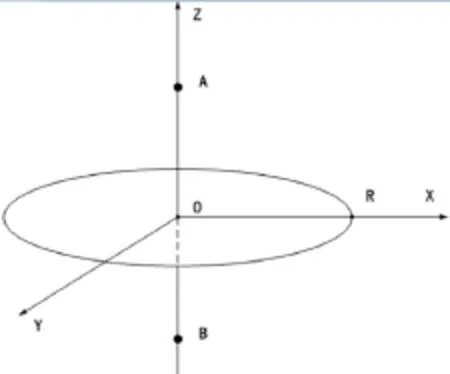
图2 线圈磁场仿真模型
在提出仿真模型和设定完仿真条件后,利用matlab得出仿真Ⅰ的结果如图3:
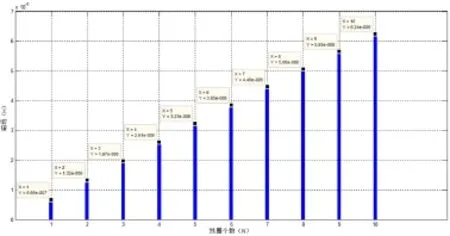
图3 仿真Ⅰ数据结果对比
然后仿真条件不变,选取线圈平面圆心O点进行磁场强度对比,仿真Ⅱ结果如图4:
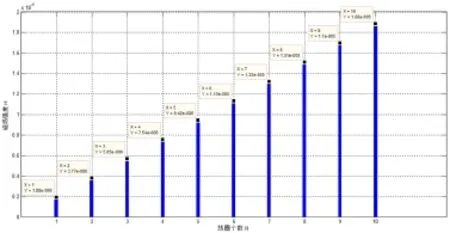
图4 仿真Ⅱ数据结果对比
同样,本次仿真实验中,还选取了和A点对称的B点进行数据对比,即在线圈平面下方,沿圆心轴线1 m的位置,得出仿真Ⅲ的数据对比图如下:
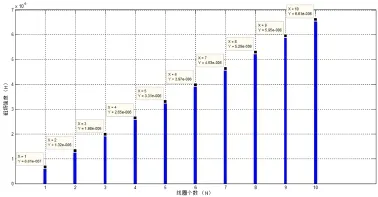
图5 仿真Ⅲ数据结果对比
为了更好的验证线圈个数叠加和磁场强度是否成线性关系,将图2圆心线圈模型的面积扩大一倍,然后选取O点进行磁场强度对比,即仿真条件变为:
1)圆形线圈,半径R=1.414 m;
2)电流I=3 A,理想方波信号输入;
3)磁场强度对比点选取为线圈平面下方,沿圆心轴线1 m的B点。
仿真Ⅳ的结果如图6所示:

图6 仿真Ⅳ数据结果对比
3 仿真结果分析
在得出不同的仿真条件下的数据后,下面对结果进行对比分析。
1)首先对比Ⅰ和Ⅱ,这两个仿真结果是为了验证在距离线圈不同的位置,磁场强度的大小和线圈叠加个数是否成线性关系,从柱状图可以明显的看出,当电流大小和线圈面积一定时,随着线圈个数的增加,所激发的磁场强度也成线性上升,且不同的位置结果一样,只是磁场强度不同。
2)然后对比仿真结果Ⅰ和Ⅲ,根据毕奥——萨伐尔定律可知,以理想圆形线圈平面为分界线,上下对称的点磁场强度大小应该一致,Ⅰ和Ⅲ正是为了验证这一点,同时仿真结果Ⅲ的存在,也更好的验证了第一种情况。从数据上可以看出,A点和B点的磁场大小在相同线圈叠加个数的情况下近似相等,且B点位置同样的磁场大小同样和线圈个数成线性关系。
3)最后分析仿真结果Ⅳ。在验证了相同仿真条件下不同位置的点磁场强度和线圈个数的线性关系后,对模型线圈的面积进行改变后,选取一个点来验证磁场强度和线圈个数是否还会是这种关系,从结果Ⅳ中可以看出,当线圈面积改变后,线圈叠加,O点的磁场强度同样成线性增加。
4 结论
本文中根据不同的仿真条件得出了4组仿真结果进行对比,比较全面的验证了线圈激发的磁场强度大小和线圈叠加个数的线性关系,验证结果和理论相符合。本次仿真使得线圈磁场线性叠加从理论到实际更进一步,这将为某些安全要求较高的特殊环境应用提供依据。
司文建,周楠,曹玉松.基于MATLAB的亥姆霍兹线圈轴线磁场均匀分布的动态仿真[J],许昌学院学报,2010,29(5):72—74.
The circular coil magnetic field strength of a linear relationship with the number of coil simulation based on MATLAB
Cheng Hai,Gong Hao,Chen Kun,Wang Haoxing,Yue Hui
(Xi’an Research Institute,CCTEG,Xi’an,710074,China)
The MATLAB software for the complex,abstract physical phenomena of dynamic simulation provides simple,efficient coding environment.Using the Biot--Savart law article in the phenomenon of current magnetic field distribution are derived based on the mathematical model of the ring,the use of MATLAB software for verification and Simulation of circular coil axis magnetic field distribution,obtained the linear relationship between the circular coil axis magnetic field intensity and the coil number analysis results.
MATLAB; circular coil;magnetic field distribution;magnetic field superposition
