柔性集装袋自动生产装备回转鼓轮机构的优化设计
2014-02-21来五星许泽霖凌思涵
来五星,许泽霖,凌思涵
(华中科技大学机械科学与工程学院,湖北 武汉 430074)
柔性集装袋是由聚丙烯、聚乙烯等聚酯纤维纺织而成的原料经过缝纫机缝纫而成,广泛用于化工、建材、塑料、矿产品、粮食、水泥等各类粉状、粒状、块状物品的包装。柔性集装袋自动生产装备是自动完成双筋圆筒柔性集装袋各个缝纫工序(吊带缝纫、腰箍缝纫和底袋缝纫)的设备,其总体布局如图1所示。该设备主要包括上料工位、卷边工位、吊带工位(两个)、腰箍工位、底袋缝纫工位、下料工位、转运小车和工位间的运输装置等。转运小车载着双筋圆筒料在各工位间运输,完成各个缝纫动作及缝纫准备动作。
1 回转鼓轮机构功能分析与设计
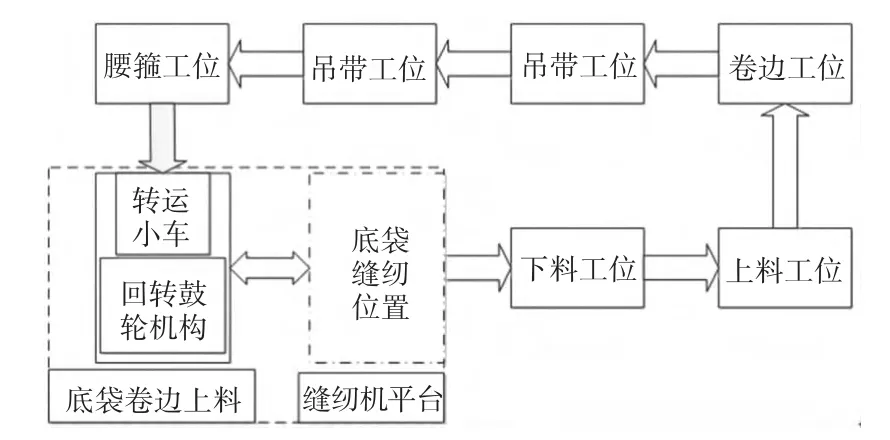
图1 柔性集装袋自动生产装备总体布局
底袋缝纫工位(图1左下角虚线框内)完成底袋上料、双筋圆筒和底袋的缝纫两大功能,其主要工作流程为将上好料的底袋和转运小车撑成四边形的双筋圆筒料配合夹持好,然后转运小车和回转鼓轮机构一起运动到底袋缝纫位置,依次将双筋圆筒料的四个面翻出缝纫平面,依靠缝纫机平台的往复运动完成缝纫机缝纫。本文所涉及的回转鼓轮机构是底袋缝纫工位中的关键机构,主要完成底袋上料和底袋缝纫的衔接、底袋缝纫等功能,因此对其进行进一步的研究,具有非常重要的意义。
1.1 回转鼓轮机构工艺过程分析
回转鼓轮机构是底袋缝纫工位中的一个关键机构,其具体所要实现的功能包括:
(1)将底袋和圆筒料夹持在一起,便于进行缝纫;
(2)所需夹持的每个“气爪机构”需要有3个自由度(两个移动,一个转动),才能完成夹持和翻出缝纫平面等所需要的动作;
(3)为了能够缝纫集装袋的四边,所有的“气爪机构”需要装在一个可以回转的鼓轮上面,且每次转动角度为90°。
1.2 回转鼓轮机构的结构与工作原理
本文研制的回转鼓轮机构如图2所示,该机构主要由支架、鼓轮座、组装鼓轮、气爪机构、电动机(YEJ系列带制动器)、减速器、链式齿圈机构和自动卷管器(解决“气爪机构”供电供气及工位间的通信问题)等组成。其中的气爪机构包括两个带导杆气缸,一个摆动气缸和一个气爪,分别实现两个移动自由度,一个转动自由度和夹持动作。
回转鼓轮机构的主要传动系统为:电动机(三相异步电动机)经过减速器(i=24.00)和链轮链条(i=112/17)两级减速,带动鼓轮旋转。为了便于分析异步电动机的启动过程,将传动系统等效到执行元件输出轴上,得到其等效模型如图3所示。电机的型号为YEJ90L-4,惯性负载(包括电机轴及传动系统等效转动惯量)J=0.05 kg/m2。当缝纫底袋的下一边时,转运小车上负责双筋圆筒料转动的伺服电机需要与鼓轮的转动相匹配,故需要建立一个双电机的匹配模型。因为双电机中伺服电机的运行可以按照异步电动机的运行曲线来加减速,下面建立三相异步电动机的运动仿真模型。
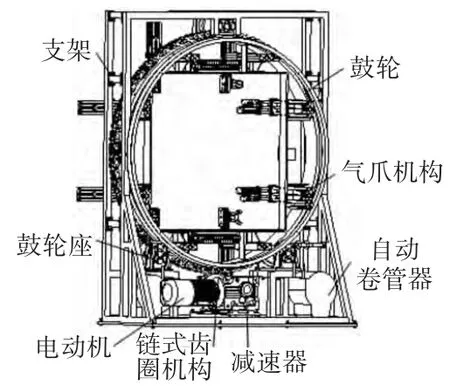
图2 回转鼓轮机构结构图
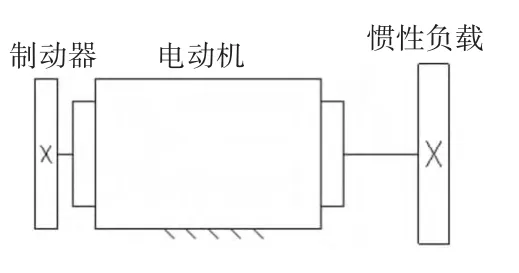
图3 鼓轮转动传动系统等效图
2 回转鼓轮机构异步电动机运行仿真
2.1 异步电动机的数学建模
异步电动机结构简单,运行可靠,价格低廉,应用十分广泛,但异步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。研究异步电动机数学模型时,作如下的假设[1]:
(1)忽略空间谐波、三相绕组对称、产生的磁动势沿气隙按正弦规律分布;
(2)忽略磁路饱和,各绕组的自感和互感都是恒定的;
(3)忽略铁心损耗;
(4)不考虑频率变化和温度变化对绕组电阻的影响。在正交定子坐标系(α-β)下,可以将异步电动机的等效电路通过Clarke变换从三相变为两相,其正交转换矩阵为:
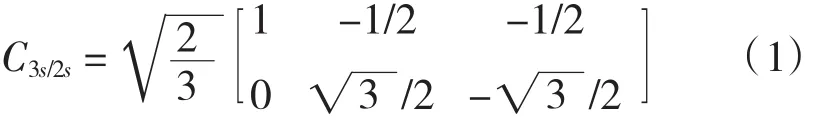
由两相变成三相的转换矩阵为:
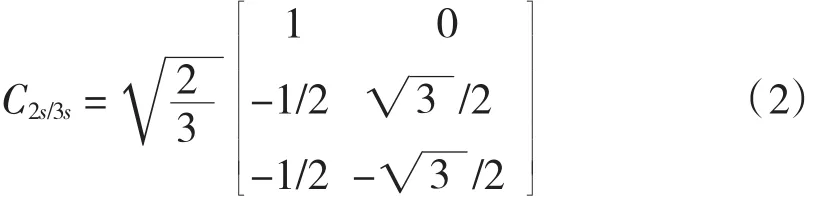
鼠笼式异步电机在静止两相坐标系(α-β)轴上的电压矩阵方程为:
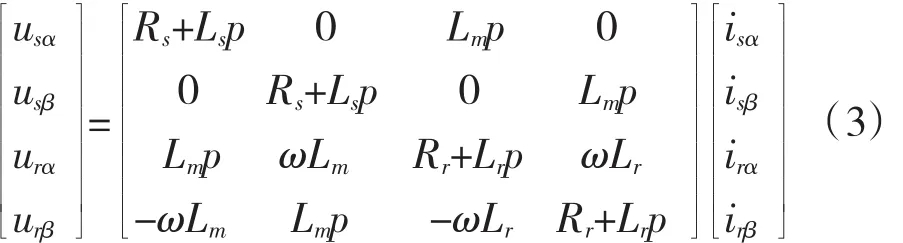
式中,
usα、usβ为异步电动机在 α、β 轴上的定子电压分量;
urα、urβ为异步电动机在 α、β 轴上的转子电压分量;
isα、isβ为异步电动机在 α、β 轴上的定子电流分量;
irα、irβ为异步电动机在 α、β 轴上的转子电流分量;
Rs、Rr为定、转子电阻;
Ls、Lr为定、转子电感;
Lm为定、转子间互感;
p为微分算子;
ω为转子机械角速度。
鼠笼式电机转子侧短路,urα=urβ=0。
磁链方程为:
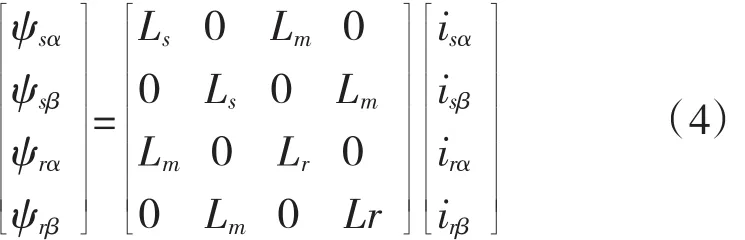
电磁转矩方程式为:
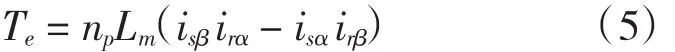
运动方程式为:
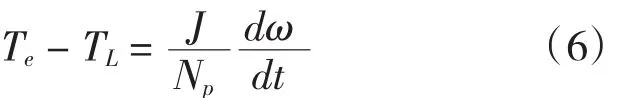
式中:
Np为电机的极对数;
J为电机的转动惯量;
TL为负载转矩。
由以上各方程,以定子和转子电流(isα、isβ、irα、irβ)和转子角速度 ω 为状态变量,以定子端电压(usα、usβ)及负载转矩 TL为输入变量,以定子和转子电流(isα、isβ、irα、irβ)和转子角速度 ω 为输出变量,可以得到恒转矩负载下的三相异步电动机的数学模型。其状态方程如下:

式中:
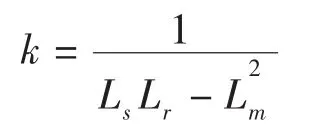
电机的实际转速:

异步电动机通过Clarke变换后,其数学模型仍是一个高阶、非线性、强耦合的多变量系统[2]。SIMULINK电力系统仿真工具箱中的电机模型以上述模型为基础,包括转子电磁、定子电磁、气隙磁链、转矩和机械运动、坐标变换和中间量计算六个子系统,可以尽可能真实的反应异步电动机的物理运行过程。下面在MATLAB/SUMULINK环境下建立上述模型的启动仿真图。
在MATLAB/SIMULINK环境下,利用POWERLIB库中模块搭建三相异步电动机启动模型如图4所示。
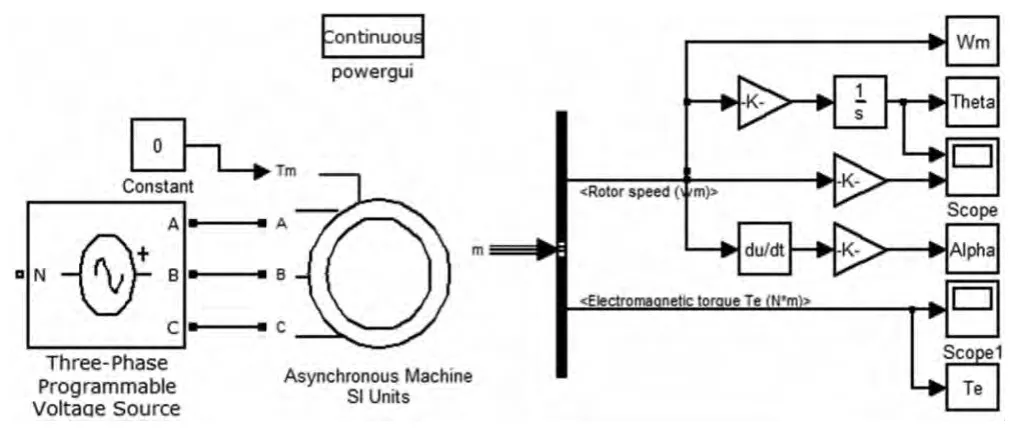
图4 三相异步电动机动态仿真模型
当异步电动机转动达到所需转数后,会切断电动机的电源,电动机会在电磁制动器制动力矩的作用下,转速逐渐减为0。该制动过程可等效为一回转物体在固定力矩作用下,做匀减速运动。其减速模型为:
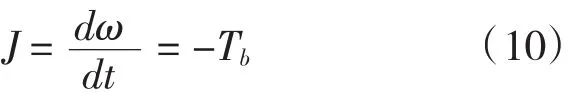
制动时间:t0=Jω/2Tb
其中,Tb为电磁制动器制动力矩。
2.2 仿真结果及分析
输入相应的电机参数:电机功率Tn=1 500 W;线电压Vn=380 W;电压频率fn=50Hz;定子电阻Rs=2.22 Ω;定子自感Ls=0.018 7 H;转子电阻Rr=2.65 Ω;转子自感 Lr=0.018 7 H;互感 Lm=0.078 9 H;转动惯量J=0.05 kg/m2;极对数为p=2,得到最后的仿真结果如图5所示。
由图5可知,电机输出转矩在开始阶段会有短时(约0~0.2 s)振荡,然后电机逐渐加速,在0.5 s的时候达到稳定转速1 493 r/min。到1.58 s的时候给电机断电,制动器开始制动,2.1 s的时候电机完全停止,鼓轮转动的角度正好为90°。那么,转运小车上的伺服电机即可按照该曲线加减速运动,达到双电机的匹配运动。
不考虑电机在开始阶段输出转矩的短时振荡,由图5可知,鼓轮在0.35s时达到最大加速度2.919rad/s2,此时电机输出转矩为23.078 2 N·m,此时鼓轮所受外力最大,下面对此情况下的鼓轮进行静力学分析。
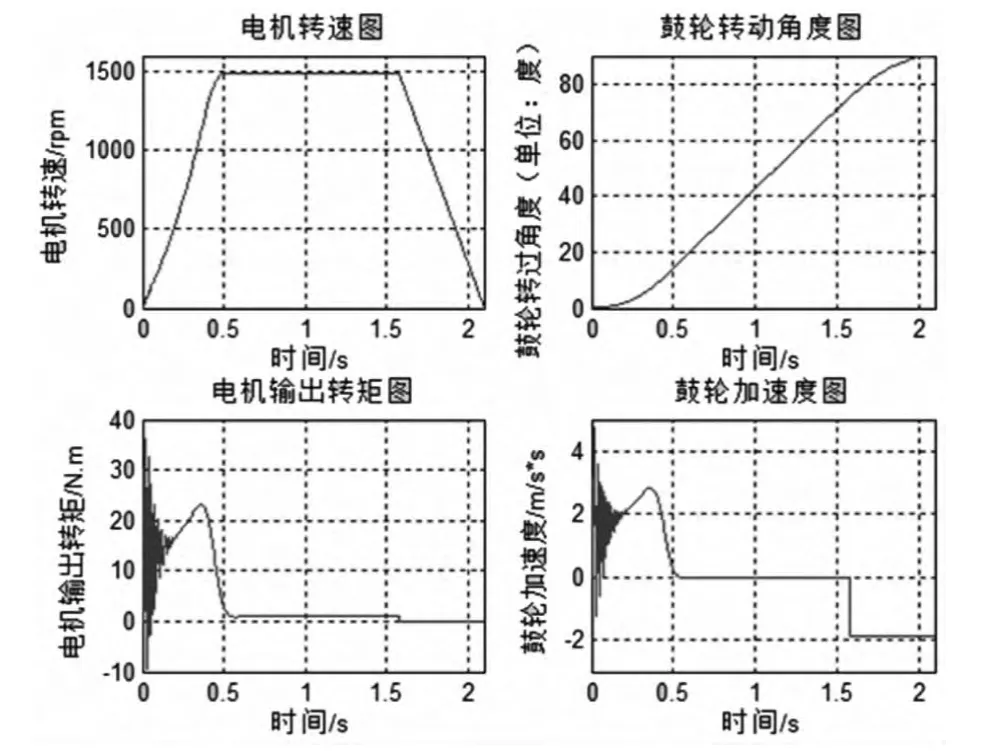
图5 仿真结果图
3 鼓轮有限元仿真及优化
3.1 静力学仿真模型的建立
(1)为了便于后续的结构优化,采用Workbench自带的几何建模模块DesignModeler建立鼓轮的三维参数化模型。建模过程中对零件部分特征进行了合理简化、合并等效,忽略了对最后结果影响很小的螺纹孔等一些复杂结构。
(2)材料定义:鼓轮机构采用的材料均为Q235,弹性模量为206 GPa,泊松比为0.25,密度7 850 kg/m3。
(3)网格划分:为了提高网格划分的质量,在DesignModeler中将模型分割成11部分,对不同部分分别采用不同的网格尺寸,细节处细化网格。最后得到的节点总数为238208,单元总数为45968,歪斜度(Skewness)最大值为0.787,网格质量满足计算要求。
(4)边界条件及载荷:采用“Fixed-Support”约束与鼓轮座的接触位置,载荷包括机构本身的重力和来自电机的外力。
3.2 静应力分析
鼓轮所受最大应力在鼓轮和鼓轮座的接触处(图6),σmax=35.394 3 MPa,所用材料的屈服极限为235 MPa,取安全系数S=6,则其许用应力值[σ]=39 MPa。鼓轮的最大变形量发生在鼓轮最上端,δmax=0.158 21 mm,允许的变形量为[δ]=D1/5 000=0.31 mm,故强度、刚度满足要求。
3.3 多目标结构优化求解
(1)优化目标:在满足强度(最大应力σmax)、刚度(最大变形δmax)的条件下,使鼓轮质量达到最小;
(2)输入参数:骨架框架钢板厚度DS_L1;骨架加强钢板厚度DS_L2;骨架钢板的宽度DS_FD1;鼓轮的内圈直径DS_D1(具体见图7);
(3)约束条件:i同上述静力学仿真模型的边界条件及载荷;ii输入参数的上下限;
(4)数学模型的建立。根据以上设计变量及约束条件的确定,得到该优化的数学模型如下:
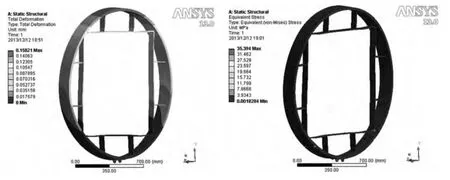
图6 鼓轮变形和静态应力分布图
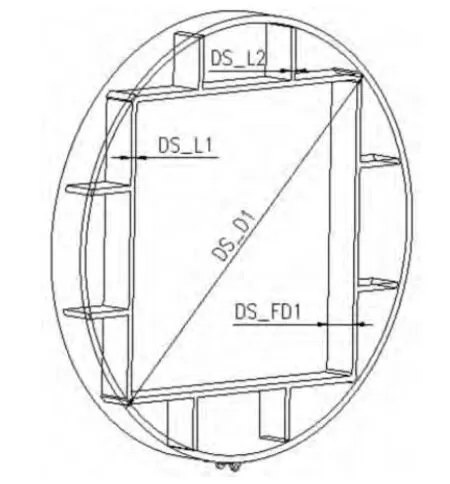
图7 输入参数尺寸图
利用Workbench经过优化求解以后,得到各输入参数对优化目标的敏感度如下图8所示,由图可知,输入参数DS_D1对三项优化目标影响都很明显。其他三个输入参数对最大应力基本都没有影响,骨架加强钢板厚度对最大变形和鼓轮质量影响比较明显,骨架框架钢板厚度对最大变形和鼓轮质量也有一定的影响。
在保证强度刚度的前提下,保证鼓轮质量最小,得到的最优方案,然后对其各尺寸进行圆整,优化前具体参数及变化与最后采取的圆整结果比较情况如表1所示。

表1 优化前与圆整后的尺寸与目标参数值
4 结束语
综上分析,我们得出以下结论:
(1)在MATLAB/SIMULINK环境下实现了对异步电动机的建模,得到了异步电动机在惯性负载下的运行特性,也为异步电动机的控制研究奠定了基础。
(2)通过Workbench进行有限元分析,得到了鼓轮在所受外力最大的工作情况下的变形和应力分布图,该设计强度和刚度均满足使用要求。
(3)利用Workbench对滚轮进行优化设计,在保证强度、刚度的条件下,使鼓轮质量由170.55 kg减少到了123.18 kg,减少了27.77%。
[1]李 明,朱美强,马 勇.MATLAB/SIMULINK通用异步电机模型的分析与应用[J].工矿自动化,2005(3):9-13.
[2]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2000.
[3]凌桂龙,丁金滨,温 正.ANSYS Workbench13.0从入门到精通[M].北京:清华大学出版社,2012.
