能量棒以颜色为劣变指标的货架期预测误差分析

钱平，董新娜，王婵，李博*，张晓娟

（1.总后勤部军需装备研究所，北京 100010；2.中国农业大学食品科学与营养工程学院，北京 100083）

实时测试（Real-time tests）和货架期加速预测测试（ASLT）都是预测食品货架期的常用方法。通常ASLT法在工业应用中更为普遍，因其可以缩短产品上市的时间[1]。货架期预测方法通常包括5个步骤：确定贮藏过程中的主要品质劣变及相对应的指标；实施货架期加速预测试验；确定感官可接受终点及相应的化学指标限值；建立数学(Arrhenius[2-3]或修正的Arrhenius[4]方程)模型，描述化学指标变化与温度的关系；通过所建模型计算常温货架期并与实际货架期比较验证。在此领域研究较多，Calligaris[5]建立了ASLT动力学模型来预测焙烤食品的货架期，并用面包为原料验证了所建模型[6]。Rahmouni[7]建立了数学模型来描述初榨橄榄油的氧化稳定性。

但ASLT方法得到的货架期存在一定误差，这些误差由预测过程中的每步误差累积而成。测定重复数会影响测定准确性；劣变曲线的拟合点数和时间间隔会影响速率常数的准确性；加速试验的温度点数和温度范围也会影响货架期预测的精确度。目前，有研究者报道了利用加速实验预测货架寿命的误差分析，张蓉晖[8]通过加速实验预测了蛋卷的货架寿命，20℃恒温环境中，在没有干燥剂和存在干燥剂条件下，货架期预测值分别为63d和75d，误差分别为9.5%和8.0%。Magari (2007)[9]通过数学模型推测影响货架期准确度的因素有测定重复、批次和试验设计。但实际预测试验中，各因素对预测误差的影响仍不确定。

本研究将从平行个数、取点个数、检测时间间隔和加速温度条件等方面探讨其对色差模型预测精度的影响，以期最大程度的提高预测精度，为同类研究提供参考依据。

1 材料与方法

1.1 材料与仪器

军用能量棒 北京总后勤部军需装备研究所研制，天津津乐园饼业有限公司生产。

DC-P3型全自动测色色差计 北京市兴光测色仪器公司；LHS-250HC-1型 恒温恒湿箱上海一恒科学仪器有限公司。

1.2 实验方法

1.2.1 感官评价确定常温货架期终点 参考 Weibull 危害分析方法[10-11]确定感官可接受终点。分别将40袋能量棒置于37、65°C恒温恒湿箱（RH=60%）中，分别每隔10d、3h随机取出4个样品，保存在4℃冰箱，待所有样品取完，一起进行感官评定。感官评定方法参考董新娜实验方法[12]以感官分析的累计危害达到 69.3%作为货架期终点[13]，应用最小二乘法对数据进行回归至累计危害达到100%。

1.2.2 能量棒以颜色为劣变指标的货架期预测模型的建立 采用ASLT法建立了能量棒以颜色为劣变指标的货架期预测模型Ln t= Ln(1/m)-（LnK)*C，其中，t代表食品贮藏寿命（d）,C代表摄氏温度（℃），K、m为参数[12]。

1.2.3 样品测定重复数对色泽货架期预测精度的影响 将能量棒放置于 37、45和 50°C（RH=75%）的恒温恒湿箱中，各温度下每个检测点分别检测 2～6次，依次每隔3、2、1d定期检测色差指标，每个温度下检测12个点。运用37、45和50°C三个温度下的实验数据，根据不同测定重复分别进行二级模型拟合，以分析不同测定重复对速率常数的影响。根据不同重复拟合得到的速率常数建立货架寿命模型（Lnk-1/T和Lnt-C），并对常温下（298K）货架寿命进行预测，并进行预测误差分析。

1.2.4 拟合点数对色泽货架期预测精度的影响 在37、45和50°C温度条件下分别取4、6、8、10、12个点进行数据处理。其它内容同1.2.1。

1.2.5 取样时间间隔对色泽货架期预测精度的影响 37°C下分别间隔2、3、4d，45°C下分别间隔2、3、4d，50°C下分别间隔0.5、1、2d，检测色差指标，其它实验内容同1.2.1。

1.2.6 加速试验温度个数，温度间隔和温度范围对色泽货架期预测精度的影响 将能量棒分别放置于37、45、50、55、60和65°C下进行加速试验，定期检测色差变化，分别建立不同温度个数，不同温度梯度，不同温度范围的Arrhenius方程和货架寿命预测模型，并进行常温货架期预测和误差分析。

1.2.7 色差测定色泽采用色差计测量, 以标准白瓷瓦片作为空白对照。样品去除包装后，用色差计光源垂直照射样品表面，分别记录L*值（亮度）、a*值（红度）和b*值（黄度）。

1.2.8 预测误差分析 本研究中选择货架寿命模型Ln t= Ln(1/m)-（LnK）*C和Arrhenius方程来预测能量棒的常温货架期并分别对其预测误差进行分析。预测误差（%）=（货架期预测值-货架期计算值）/货架期计算值×100

2 结果与分析

2.1 常温货架期确定

将感官结果按weibull分布拟合后，对应累积危害69.3%的的贮存时间为19.9d，此时色差亮度L*为33.06。因此，将33.06作为颜色的感官可接受终点。测定25°C下能量棒色差L变化，到终点33.06时所需时间为426d，即为常温实际货架期。

2.2 货架寿命模型的预测误差分析

2.2.1 样品平行个数、试验检测点数和检测时间间隔对模型预测精度的影响 将能量棒分别放置于37、45和50°C恒温箱中，按照不同取样个数，不同取点个数，不同时间间隔分别定期检测色差，建立37、45和50°C的货架寿命预测模型（Lnt-C），进行常温货架期预测。从表1中可以看出，试验平行个数，检测点数个数和检测时间间隔的不同对能量棒货架期预测精度有一定的影响，货架寿命预测模型的拟合程度较高，均在 0.94以上，预测常温货架期偏小。

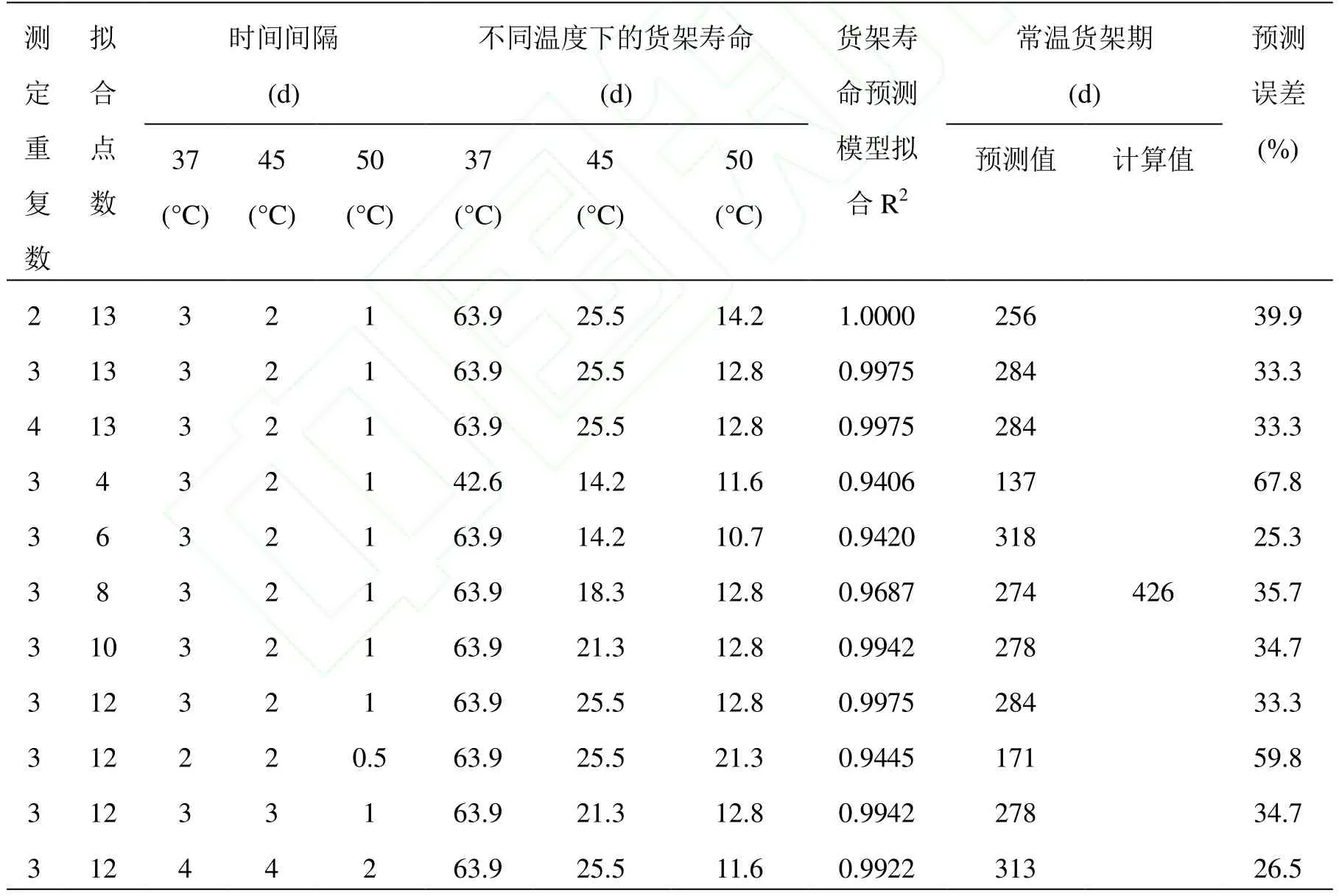
表1 样品平行个数/试验检测点数、检测时间间隔对货架寿命模型预测精度的影响Table1 The effect of sample numbers, plot numbers, interval of testing time on prediction precision using half-experienced shelf life prediction equations

当检测点数和时间间隔一定时，不同试验平行个数对预测结果稍有影响，但不同取点个数之间变化不大，常温货架期预测值仅相差30d左右，且货架寿命预测模型拟合的回归系数均在0.99以上，差别不大，确定取样个数为3个；当试验平行个数和检测时间间隔一定时，拟合点数对货架期预测有一定的影响，随着拟合点数的增加，货架寿命预测模型拟合系数逐渐增大，预测常温货架期逐渐增大，预测精度逐渐提高，当取点个数由4个增加至12个数，精度提高近一倍，误差减小34%，且精度提高的幅度逐渐增大，因此确定取点个数为12个；当试验平行个数和拟合点数一定时，检测时间间隔对货架期预测也有一定的影响，随着时间间隔的逐渐增加，预测误差逐渐减小，37°C下间隔4d，45°C下间隔4d，50°C间隔2d时，预测误差为26.5%，减小33%。

2.2.2 加速温度条件对模型预测精度的影响 将能量棒分别放置于 37、45、50、55、60和65°C恒温箱中，定期检测色差，建立不同温度个数，不同温度梯度，不同温度范围下的货架寿命预测模型（Lnt-C），进行常温货架期预测。

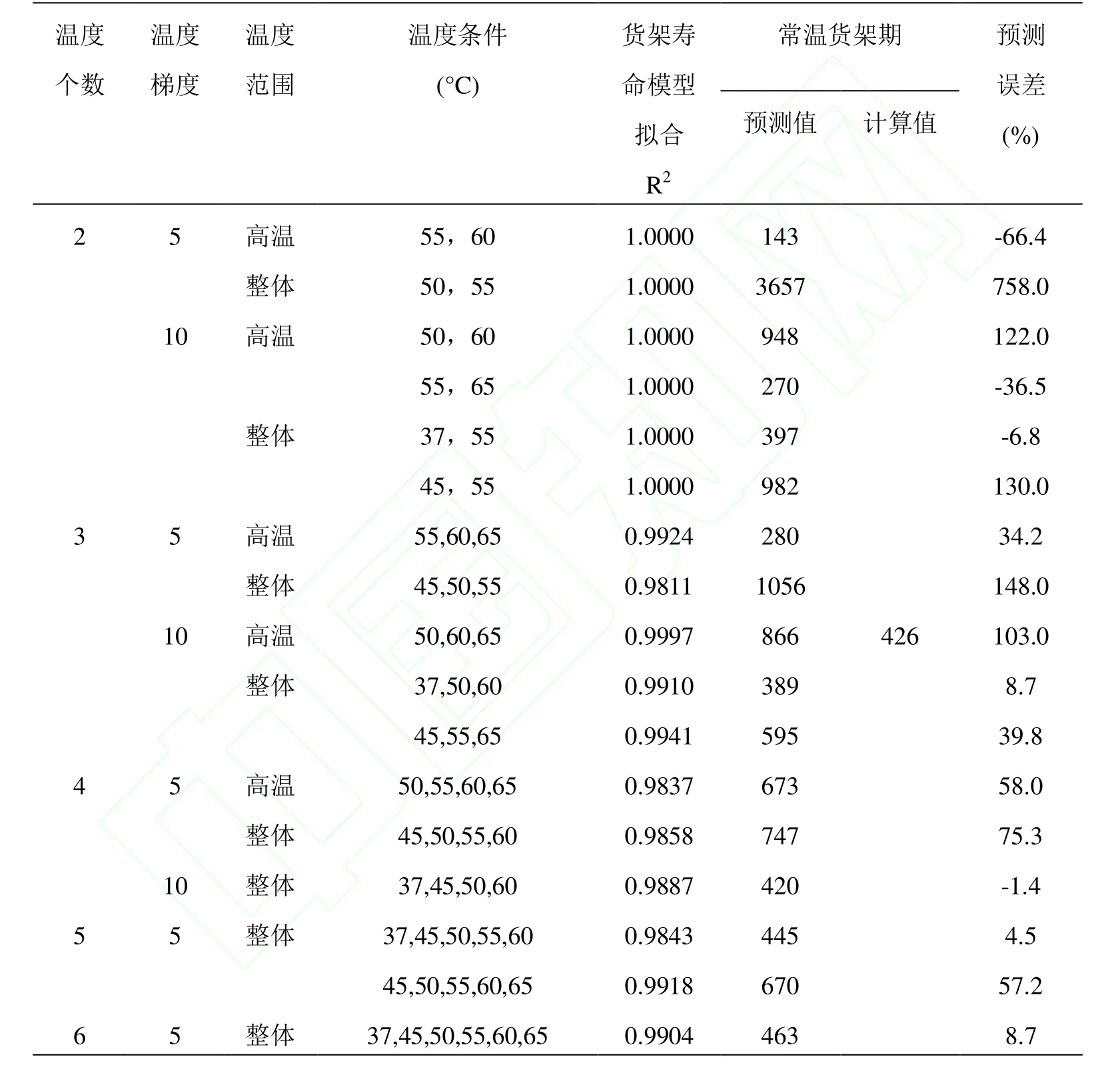
表2 加速温度条件对货架寿命模型预测精度的影响Table2 The effect of accelerated temperature conditions on prediction precision using half-experienced shelf life prediction equations

由表2可看出，货架寿命预测模型的拟合系数整体较高，均在0.98以上，最高为0.9997（2个温度的除外），不同加速温度条件对货架寿命模型Ln t= Ln(1/m)-（LnK）*C货架期预测精度影响十分显著，预测误差相差很大。

2.2.2.1 温度范围的影响 温度范围对模型预测精度影响比较大，当温度个数，温度梯度一定时，在整体范围下建立的货架寿命预测模型比仅在高温下建立模型预测精确度要高，误差较小。当温度个数为2个，温度梯度为5°C时，整体温度范围的模型预测最小误差为6.8%，高温范围下的最小误差为36.5%；当温度个数为3个，温度梯度为10°C时，高温范围建立模型的误差为103%，整体温度范围预测误差在5～40%，精确度提高较为明显。当温度个数为5个，温度梯度为5°C时，较高温度范围建立模型的预测误差为57.2%，整体温度范围建立的模型预测误差可降低到4.53%，降低幅度非常明显。

2.2.2.2 温度梯度的影响 温度梯度对能量棒货架寿命模型预测精度影响明显，当温度个数和温度范围一定时，10°C温度梯度建立模型的预测误差明显小于5°C温度梯度。从表2可知：2个温度，高温下建立模型时，10°C梯度的模型预测误差范围在35%～150%之间，而5°C误差较大；整体温度下建立模型时，10°C梯度的模型最小预测误差为6.8%，而5°C梯度最小预测误差为66.4%。相似的，4个温度，整体温度范围建立模型时，10°C梯度预测常温货架期为420d，误差仅为1.37%，5°C梯度预测误差在50～80%以上。

2.2.2.3 温度个数的影响 温度个数对货架寿命模型预测精度影响非常显著，当温度梯度和温度范围一定时，随着温度个数的增加，预测误差范围逐减小，预测精度逐渐提高。温度梯度为5°C，高温范围建立模型，2个温度点时，预测误差最大，4个点时减小到75.3%，减小幅度明显；整体范围建立模型，2个点时预测误差为5～150%，3个点时为5～100%，4个点时小于10%，误差仅为1.37%，减小趋势非常明显。温度梯度为10°C时变化规律相同，高温范围和整体范围建立模型时，预测误差均随温度个数的增加而大大减小。

因此，确定温度个数为4个，温度梯度为10℃，在整体温度下建立预测模型，以37、45、50和60℃为实验温度，此条件下，预测常温货架期为420d，预测误差为1.37%，小于已报道的±10%左右的预测误差[14-15]。

2.3 Arrhenius方程预测误差分析

2.3.1 样品平行个数/试验检测点数和检测时间间隔对Arrhenius方程预测精度的影响

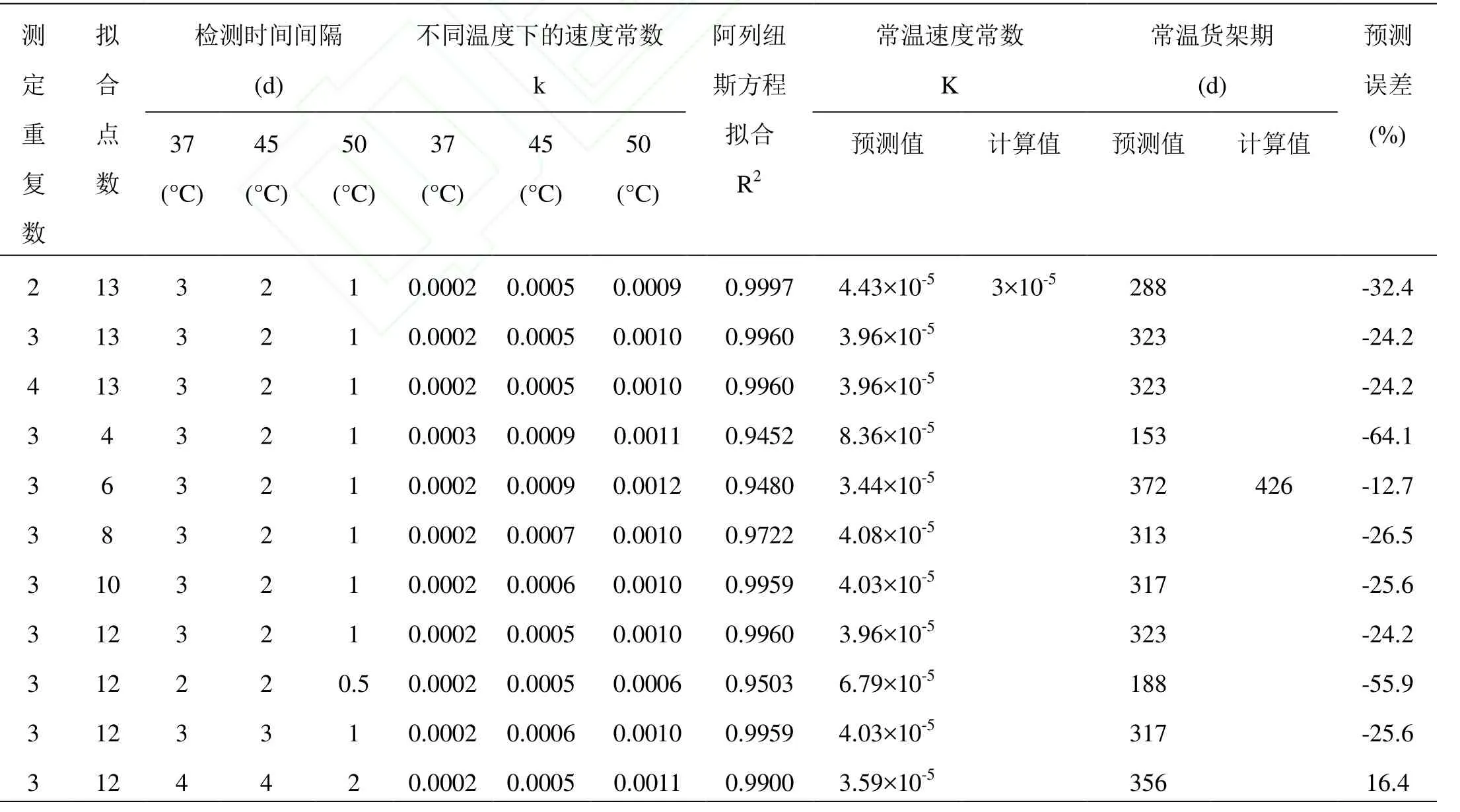
表3 样品平行个数，试验检测点数，检测时间间隔对阿列纽斯方程预测精度的影响Table3 The effect of number of replicates, number of fitting points, time interval of sampling on prediction precision using Arrhenius equation

从表3中可以看出，Arrhenius方程的拟合系数都很高，常温速度常数预测值偏小，货架期预测值偏大，预测误差偏大。当检测试验点数和时间间隔一定时，随着平行的增加，Arrhenius方程拟合系数变化不大，均在0.99以上，预测误差稍有减小，表明取样个数对模型预测精度影响较小；当平行个数和时间间隔一定时，随着检测试验点数的增加，45、50°C的反应速度常数k基本呈下降的趋势，Arrhenius方程拟合相关系数逐渐增加，货架期预测误差逐渐减小，从64.1%减小到24.2%，降低了40%，表明取点个数对模型预测精度影响较大；当试验平行个数和试验检测点数一定时，随着检测时间间隔的增加，Arrhenius方程拟合相关系数逐渐增加，常温货架期预测值逐渐减小，预测误差明显降低，从 55.9%降低到16.4%，降低约40%，这表明时间间隔对模型预测精度的影响也比较大。

2.3.2 加速温度条件对Arrhenius方程预测精度的影响

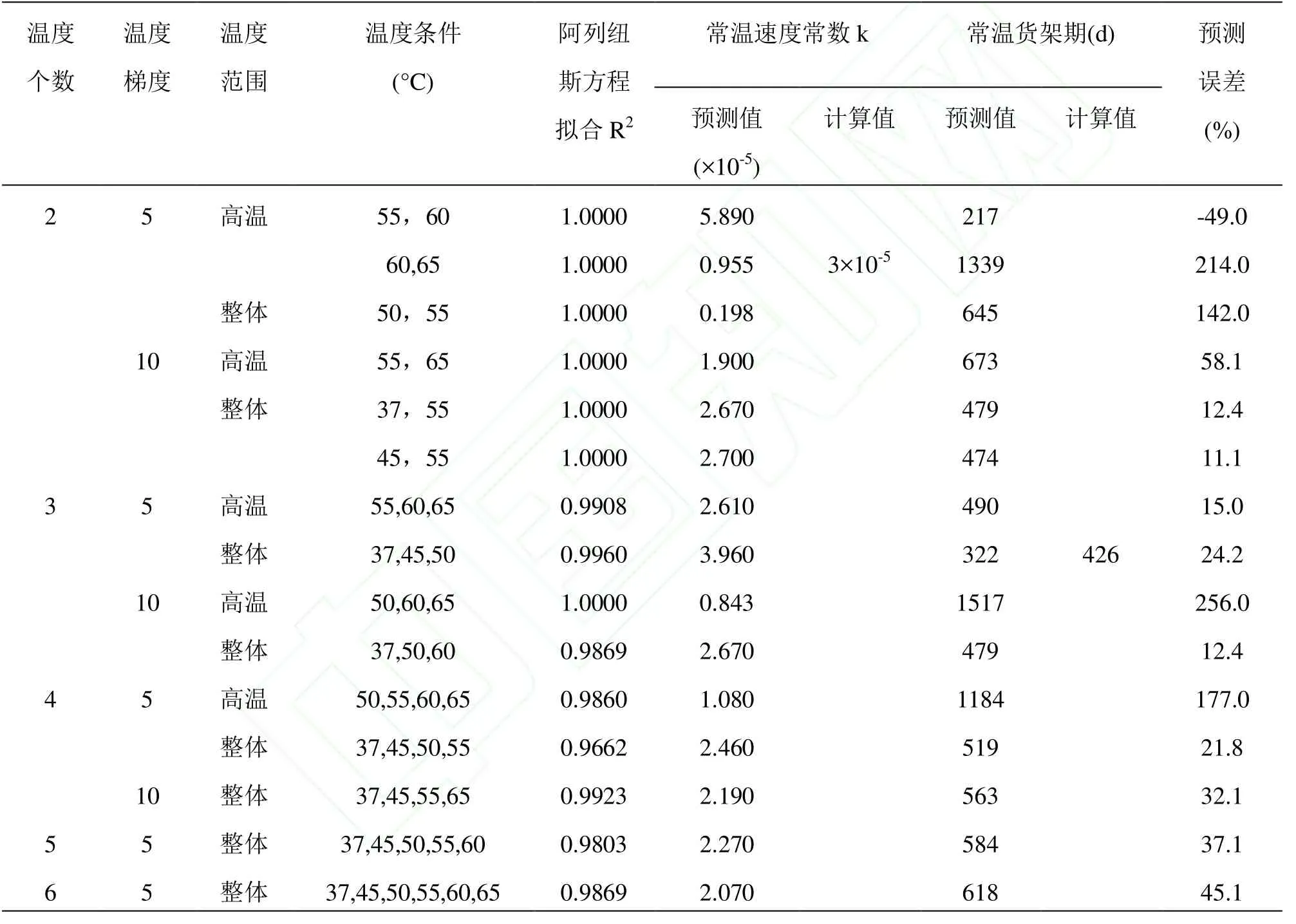
表4 加速温度条件对阿列纽斯方程预测精度的影响Table4 The effect of accelerated temperature conditions on prediction precision using Arrhenius equation

从表4中整体看，Arrhenius方程的拟合系数较高，均在0.97以上，最高为0.9999（2个温度的除外），不同加速温度条件对Arrhenius方程货架期预测精度影响十分显著，预测误差相差很大，最大值为257%，最小值为11.1%。温度个数、温度梯度和温度范围对Arrhenius方程预测精度影响都比较显著，随着加速温度个数、温度梯度和温度范围的增加，预测误差逐渐减小，误差范围从214%～12.4%。在整体温度下建立预测模型，采用37、50、60℃的加速温度，此条件下预测常温货架期为 479d，预测误差最小为 12.4%，与已报道的货架期预测误差（±10%左右）相近[14-15]。

3 结论

加速试验条件对货架寿命预测模型Ln t= Ln(1/m)-（LnK）*C和Arrhenius方程预测精度的影响相同。两种预测方法在相同条件下的预测结果不同，预测精度有差异，运用货架寿命预测模型预测常温货架期的精确度明显优于运用Arrhenius方程。加速温度条件对预测误差的影响最大，随着温度个数的增加，预测精度逐渐提高；且整体温度范围内建立的货架寿命模型比仅在高温下建立的模型预测精确度高。针对能量棒货架期色差预测试验，确定初级模型条件：试验平行个数为3个，每个温度下取点个数为12，在此基础上，选取较短的时间间隔即37°C每4d、45°C每4d、50°C每2d；加速温度条件为：37、45、50、60°C，预测常温货架期为420d，预测误差为1.37%。

[1]Davies O L, Hudson H E.Stability of drugs: accelerated storage tests.Statistics in the pharmaceutical industry [J].1982, 2:445-480.

[2] 张丽平, 余晓琴, 童华荣.Weibull模型在板鸭货架寿命预测中的应用[J].食品科技，2010, 35（2）:111-113.

[3] 曹平, 于燕波, 李培荣.应用Weibull Hazard Analysis方法预测食品货架寿命[J].食品科学, 2007, 28（8）：487-491.

[4] Kwolek W F, Bookwalter G N.Predicting storage stability from time-temperature data [J].Food Technology, 1971, 25 (10):1025-28.

[5] Calligaris S, Manzocco L, Kravina G.Shelf-life modeling of bakery products by using oxidation indices [J].Food Chemistry, 2007, 55(5):2004-2009.

[6] Calligaris S, Pieve S D.Shelf Life Prediction of Bread Sticks Using Oxidation Indices: A Validation Study [J].Journal of Food Science, 2008,73(2):51-57.

[7] Rahmouni K, Bouhafa H, Hamdi S.Development and validation of a mathematical model for olive oil oxidation [J].AIP Conference Proceedings, 2009, 1107:49-53.

[8] 张蓉晖，肖凯军.利用动力学理论预测蛋卷货架寿命的研究[J].食品研究与开发,2001,22(5):51-53.

[9] Magari R T.Uncertainty of measurement and error in stability studies [J].Journal of Pharmaceutical and Biomedical Analysis, 2007, 45:171-175.

[10] Gacula M C.The design of experiments for shelf life study [J].Journal of Food Science, 1975, 40: 399-403.

[11] Gacula M C, Kubala J J.Statistical models for shelf life failures [J].Journal of Food Science, 1975, 40: 404-409.

[12] 董新娜.军用能量棒货架期预测技术研究[D].北京：中国农业大学,2012,17-27.

[13] Cardelli C, Labuza T P.Application of weibull hazard analysis to the determination of the shelf life of roasted and ground coffee [J].Lebensm Wiss u Technol, 2001, 34(3): 273-278.

[14] 焦健，向传万.风味花生粉基于温度变化的氧化货架寿命预测[J].食品工业，2012,33(10):1-3.

[15] 谢主兰，陈龙，雷晓凌，等.采用挥发性盐基氮动力学模型预测低盐虾酱的货架寿命[J].现代食品科技，2013,29(1):29-33.