基于投影寻踪的低频振荡阻尼预测
2014-02-18王乙斐
党 杰,王乙斐
0 引言
随着电网互联程度的不断提高,系统规模越来越庞大,运行方式越来越复杂,低频振荡问题日渐凸现,已成为危及大规模互联电网安全稳定运行的主要因素之一[1~5]。
近年来,国内外的学者对低频振荡起振的条件和机理以及抑制的措施等方面进行了不断的探索和详细的分析,也取得了大量的研究成果[6~10];然而由于互联电网的复杂性,低频振荡问题仍未得到有效解决。笔者认为,应借鉴电力系统三道防线的概念,分别从以下3 个阶段对低频振荡现象进行认知、预防和控制:其一,在发电侧设计合理的防止低频振荡的励磁控制;其二,利用低频振荡在线预警系统进行预防控制;最后,当低频振荡事故发生时,采取紧急控制防止事故蔓延。
目前,研究低频振荡的方法主要是针对系统已检测到的振荡曲线判断低频振荡是否发生,此类方法不能做到防患于未然。事实上,在电网的运行状况发生改变时,如果能够根据系统的实测数据及时掌握系统阻尼的变化情况,对低频振荡模式的阻尼做出准确预测,即可对电力系统可能产生的弱阻尼模式采取及时的控制措施,有效防范低频振荡的发生。
基于此,本文利用投影寻踪方法,建立对低频振荡进行阻尼预测的数学模型,把描述电力系统运行特性的高维数据通过某种组合投影到低维子空间上,在低维空间上对数据结构进行分析。此方法成功克服高维数据的“维数灾”问题,能够对振荡模式的阻尼进行准确预测。该方法的准确性和实用性在华中电网的工程实际中得到了有效验证,从而为电力系统低频振荡问题的解决创造了条件。
1 投影寻踪基本原理
随着科学技术的发展,高维数据的统计分析越来越普遍,也越来越重要,如遥感卫星数据、GIS 中的大量数据、电力系统中广域测量信息系统(WAMS)的数据分析等。
多元统计分析是解决这类问题的有力工具。传统的多元统计分析方法是建立在总体服从某种分布,比如正态分布,这个假定的基础上的,采用证实性数据分析方法(Confirmatory Data Analysis,简称CDA),即“假定—模拟—检验”的方法。但在实际问题中有许多数据并不满足正态分布,需要用稳健的或非参数的方法去解决。然而,当数据维数很高时,这些方法都将面临一些困难:随着维数的增加,计算量迅猛增大;对于高维数据,存在高维空间中点稀疏的“维数灾”,非参数方法也很难使用;低维时,稳健性能好的统计方法用到高维时稳健性变差。因此,传统的CDA方法对于高维非正态、非线性数据分析很难得到很好的效果[11]。
投影寻踪 (Projection Pursuit,即PP)是20世纪70 年代由美国科学家Kruskal 提出的一种用来分析和处理高维观测数据,尤其是非线性、非正态高维数据的一类新兴统计方法,是应用数学、统计学和计算机技术的学科交叉,属前沿领域[11]。其基本思想是:利用计算机技术把高维数据通过某种组合投影到低维子空间上,寻找出能反映原高维数据结构或特征的投影;再在低维上对数据结构进行分析,以达到分析研究高维数据的目的。该方法的优势在于:它能够在低维子空间上进行数据分析,可成功克服高维数据的“维数灾”;另外,投影寻踪与其他非参数法一样,虽然是以数据线性投影为基础,但它寻找的是线性投影中的非线性结构,可用来解决某些非线性问题。
2 投影寻踪阻尼预测模型
投影寻踪阻尼预测模型的建模过程包括以下几步:
(1)样本预测因子集的归一化处理
为消除各预测因子的量纲、统一各预测因子的变化范围,首先必须对样本的预测因子集进行归一化处理。假设x'(i,j)为第i 个样本第j 个预测因子值,则各预测因子值的样本集为{x'(i,j)| i=1,2,…,n;j =1,2,…,p},其中n,p分别为样本个数和预测因子的数目。归一化的方法有很多,如:对越大越优的预测因子可采用:
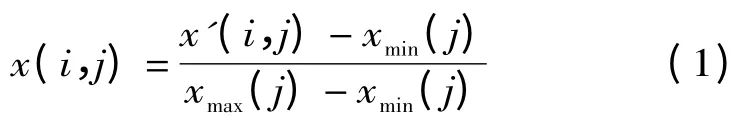
式中:xmin(j)为第j 个指标值的最小值;xmax(j)为第j 个指标值的最大值;x (i,j)为预测因子特征值归一化后的序列。
对越小越优的预测因子可采用:

本文采用标准化值,即:
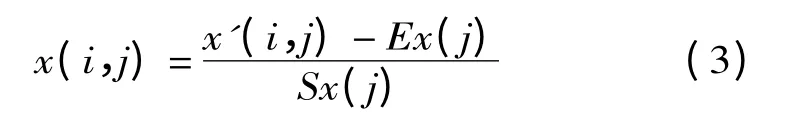
式中:Ex(j),Sx(j)分别为第j 个预测因子x(j)的均值和标准差。
(2)构造投影指标函数Q(a)
设预测对象的样本为{y(i)|i =1,2,…,n},把p 维数据{x(i,j)|j =1,2,…,p}综合成为以a ={a(1),a(2),…,a(p)}为投影方向的一维投影值z(i),即:
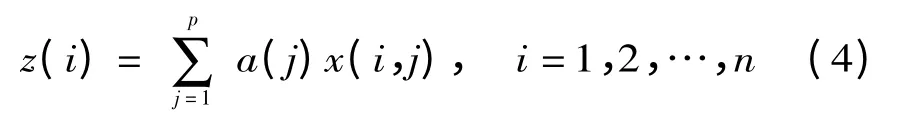
式中:a 为单位长度向量。然后根据z(i) ~y(i)的散点图建立适当的数学模型。
综合投影预测因子值时,要求投影值z(i)应尽可能大地提取x(i,j)中的变异信息,即z(j)的标准差达到Sz尽可能大,即:
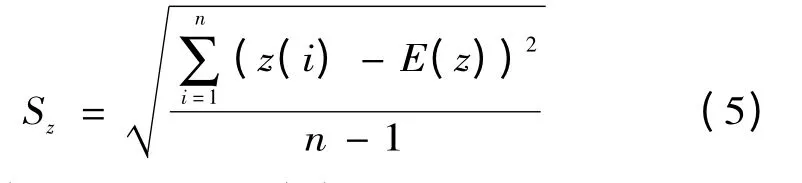
式中:E(z)为序列{z(i) | i =1,2,…,n}的平均值。
同时要求z(i)与y(i)的相关系数的绝对值| Rzy| 达到尽可能大。这样得到的投影值就可望能尽可能多地携带预测因子样本集{x(i,j)| i =1,2,…,n;j=1,2,…,p}的变异信息,并且能够保证投影值对预测对象y(i)具有很好的解释性;即局部投影点尽可能密集,最好凝聚成若干个点团,而在整体投影点团之间应尽可能散开。因此,投影指标函数可以构造成:

式中:Rzy为z(i)与y(i)的相关系数,即:
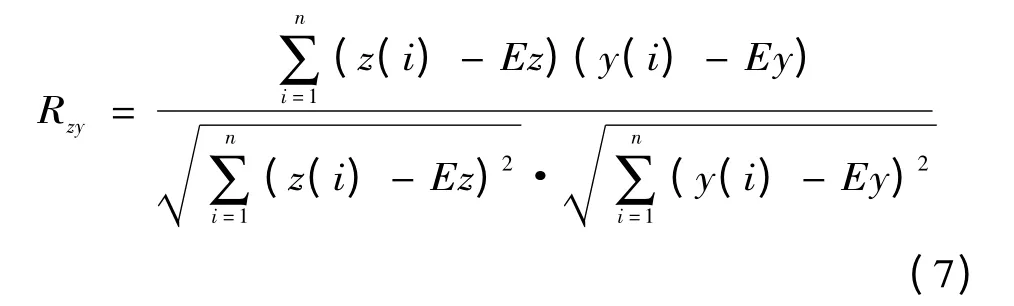
式中:Ez 和Ey 分别为序列{z(i)| i =1,2,…,n}和{y(i)| i=1,2,…,n}的平均值。
(3)优化投影指标函数
通过求解投影预测因子函数最大化问题来估计最佳投影方向,即:
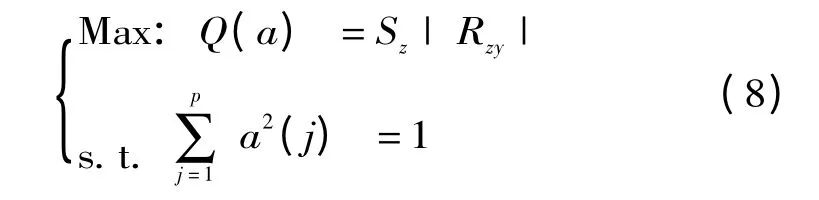
这是一个以a ={a(1),a(2),…,a(p)}为优化变量的复杂的非线性优化问题,用传统的优化方法处理较难;本文采用PSO 粒子群优化算法来解决全局寻优问题[12~15]。
(4)用门限回归 (Threshold Regression,简称TR)模型描述投影值与预测对象之间的非线性关系
TR 模型能有效地描述具有突变性、准周期性、分段相依性等复杂现象的非线性动态系统,门限的控制作用保证了TR 模型预测精度的稳健性和广泛的适应性。
把上一步求得的最佳投影方向a*代入式(4)后可得各样本点的投影值z*(i)。当z*(i)~y(i)的散点图中的点群大致呈分段线性分布时,就可采用分段线性模型来描述投影值与预测对象之间的关系。基于此,用如下TR 模型描述z*(i)~y(i)间的非线性关系:
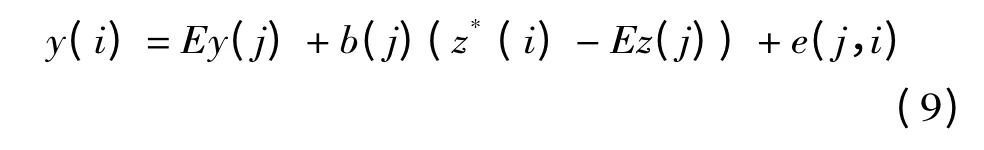
r(0)= - ∞,r(L)= + ∞,r(j)(j =1,2,…,L-1)为门限值,L 为门限区间的个数。
e(j,i)对每一个固定的j 是固定方差的白噪声序列。
Ez(j),Ey(j)分别为对应z*(i)落在门限区间[r(j-1),r(j)]中的样本点z*(i)和y(i)的均值。
b(j)为第j 个门限区间内的回归系数,为待定模型参数。
(5)用相关分析技术确定门限变量和门限延迟步数d
Rzy为z(i)与y(i)的相关系数,把相关系数绝对值最大的z*(i)作为门限变量,d 为y(i)与门限变量之间的时移相关系数最大值所对应的时移。
(6)确定门限区间个数L 和门限值r(1)~r(L-1)的寻优范围
根据分段线性的段数来确定门限区间的个数L,在分段线性的转折点附近确定各门限值r(1)~r(L-1)的搜索范围,从而减少寻优的工作量。
大多数模型都只有两个门限区间,此时只需对一个门限值r(1)寻优。综合现有的文献可知,r(1)可表征时间序列的均值特性,所以可将Ez(j)的一个领域作为r(1)的搜索范围,计算开始时直接在此范围寻优。
(7)用PSO 粒子群优化算法优化各门限值r(1) ~r(L-1)和各回归系数b(j)
可以直接在模型的最小二乘估计准则下优化,即通过求解如下最小化问题来确定:
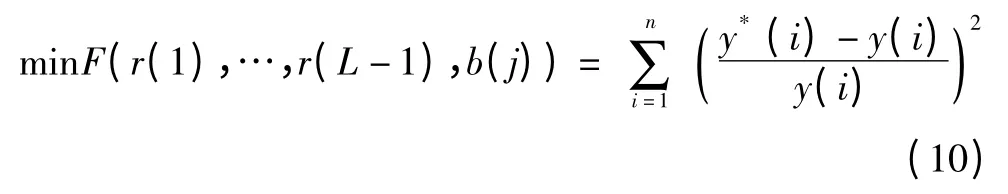
式中:y*(i)为把z*(i)代入式(9)中除白噪声以外所得预测对象的计算值,它是各门限值r(1)~r(L-1)和各门限区间内回归系数b(j)的函数。
(8)阻尼预测
按y*(i)值从大到小排序,可以将样本从优到劣进行排序,知道哪种运行方式对系统阻尼较不利。
根据最佳投影方向,可以进一步分析各个预测因子对最后评价结果的影响程度,即将a*值进行排序得到各个预测因子的贡献率大小。在此也可进一步了解哪些因素恶化系统阻尼最明显。
3 投影寻踪在低频振荡阻尼预测中的应用
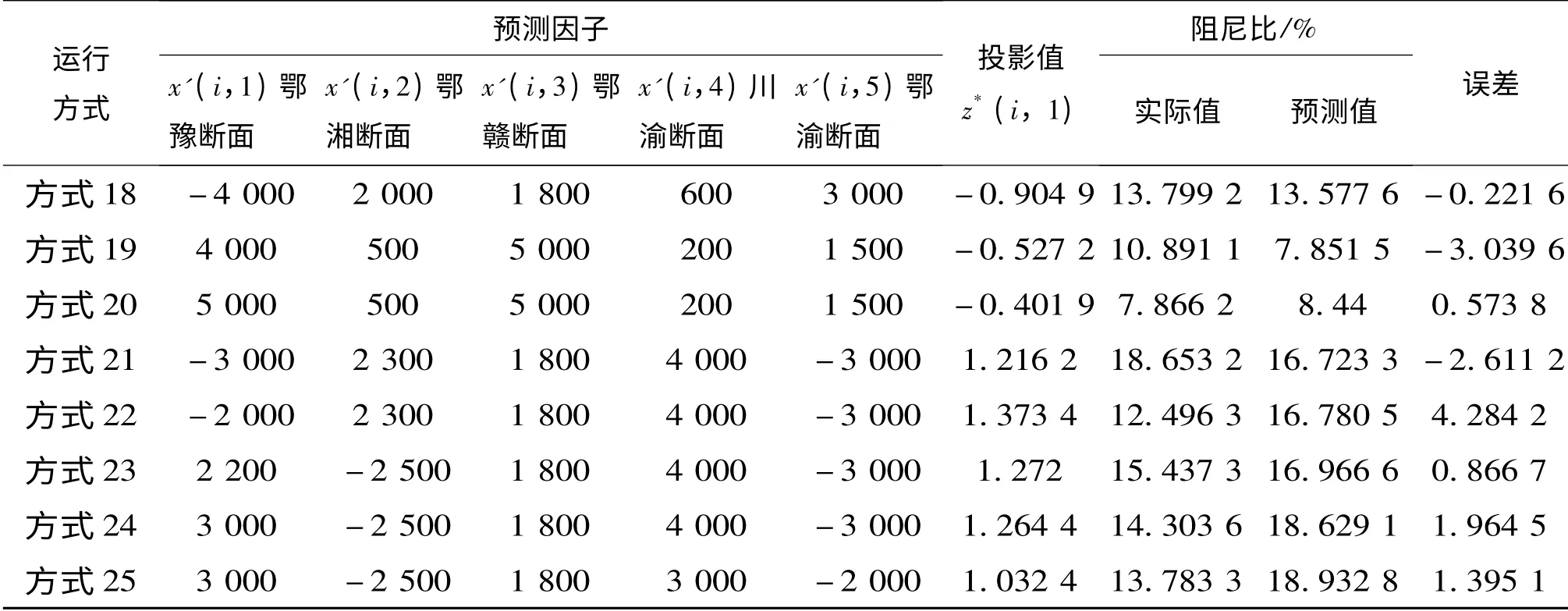
将上文建立的投影寻踪阻尼预测模型用于分析华中电网的低频振荡模式。表1 给出川豫振荡模式在25 种不同运行方式下的系统阻尼y(i),i=1,2,…,25,及其有关的5 个预测因子的值,其中5 个预测因子分别为:
z'(i,1):鄂豫断面潮流,以鄂送豫潮流为正,豫送鄂为负。
z'(i,2):鄂湘断面潮流,以鄂送湘潮流为正,湘送鄂为负。
z'(i,3):鄂赣断面潮流,以鄂送赣潮流为正,赣送鄂为负。
z'(i,4):川渝断面潮流,以川送渝潮流为正,渝送川为负。
z'(i,5):鄂渝断面潮流,以鄂送渝潮流为正,渝送鄂为负。
首先利用表1 的25 组数据建立投影寻踪门限回归模型。由于样本数量有限,用表1 中的任意24 个样本建模,预留1 个样本作预测。为了验证该方法预测的准确性,第二次选择预留另一个样本作预测。这样循环多次,在样本数量有限的情况下,既可保证建模样本的数量,又能证明预测的准确性。如表1 中,就是预留方式13 作为预测数据,其余作为建模数据,得到的结果。
把建模样本根据式(3)转换成标准化序列,依次代入式(4)~(8),得到投影指标函数的值为0.630 5,最佳投影方向为a*= [0.299 3,0.313 7,-0.063 9,0.674 7,-0.593 9]。
把a*值代入式(4)后即得各样本点的投影值的计算值z*(i),见表1。z*(i)~y(i)的散点图见图1。从散点图可以看出,散点明显分成2 部分,可以用门限回归的方法用2 条直线分别拟合左右两部分的散点。

图1 z* (i) ~y(i)的散点图
续表
图1 表明,可用式(9)来描述图1 所示的z*(i)与y (i)之间的关系。式(9)中的模型参数L=2,b (1)和b (2)通过PSO 粒子群优化算法得到。最后得到的川豫振荡模式的阻尼预测模型为:
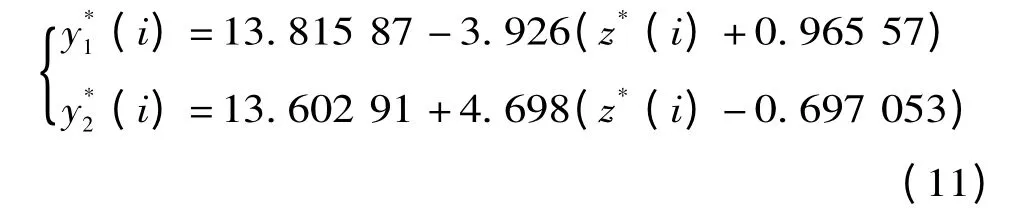
式中:y*(i)为与z*(i)对应的阻尼值。用式(11)进行拟合检验和预测检验,结果如表2 所示。表中拟合一栏是对24 组数据进行统计的结果,预测是对运行方式13 的统计。若预留其它方式做预测,结果也是类似的。若样本数据的数量加大,预测和拟合的效果更好。
由表2 知:
(1)若以阻尼比小于5%的绝对误差为合格,则阻尼预测模型的拟合合格率和预测合格率均为100%,这在工程上是完全可以接受的。
(2)若以相对误差小于30%为合格,则除运行方式3 和运行方式4 不合格以外,阻尼预测模型的拟合合格率为92%,预测合格率均为100%;运行方式3 和运行方式4 可以看成是坏数据。
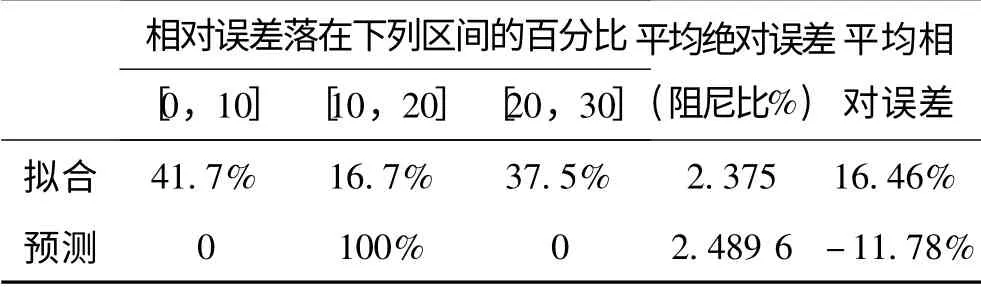
表2 阻尼预测中的拟合检验和预测检验
(3)阻尼预测模型由于有了门限的控制作用,可描述系统阻尼特性这一非线性复杂动态系统的问题。
(4)阻尼预测模型的拟合精度和预测精度是一致的,显示出稳健的预测性能。
4 结论
本文提出了一种基于投影寻踪的阻尼预测方法。该方法有别于已有的基于实测的低频振荡在线预测,不是在已检测到的系统振荡曲线上判断低频振荡是否发生;而是对有限的系统振荡模式进行高维数据统计分析,在事故发生前预测系统在当前运行方式下的阻尼情况,从而判断系统是否会发生低频振荡,以及可能发生的低频振荡模式。结合华中电网工程实际验证了该方法的有效性和准确性,从而为低频振荡的在线监测和预防控制提供了一种新的技术手段。
[1]朱方,赵红光,刘増煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报,2007,27(1):1-7.
[2]曾正,刘涤尘,向农,等.广域系统低频振荡的谐振传播 机 理 [J].电 力 科 学 与 工 程,2010,26(11):29-33.
[3]胡炳杰,赵书强,陈彩凤.应用正规形理论的电力系统低频振荡分析[J].电力科学与工程,2009,25 (2):10-12.
[4]朱方,汤涌,张东霞,等.我国交流互联电网动态稳定性的研究及解决策略[J].电网技术,2004,28(15):1-5.
[5]王洪涛,刘玉田,雷鸣,等.电网互联对山东电网内部低频振荡模式的影响[J].中国电力,2004,37 (6):12-15.
[6]吴海霞,常勇.低频振荡广域监控研究现状及新进展[J].高电压技术,2008,34 (8):1737-1744.
[7]张鹏飞,罗承廉,孟远景,等.电力系统低频振荡的广域监测与控制综述[J].电网技术,2006,30 (增刊):157-161.
[8]邱夕兆,于占勋,雷鸣,等.山东电网基于WAMS 的低频振荡统计与评估[J].电力系统自动化,2008,32(6):95-98.
[9]鞠平,谢欢,孟远景,等.基于广域测量信息在线辨识低频振荡[J].中国电机工程学报,2005,25 (22):56-60.
[10]韩松,何利铨,孙斌,等.基于希尔伯特—黄变换的电力系统低频振荡的非线性非平稳分析及其应用[J].电网技术,2008,32 (4):56-60.
[11]付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.
[12]唐权,吴耀武,熊信银,等.SA-PSO 在水火电混合电力系统电源规划中的应用[J].高电压技术,2006,32 (4):104-107.
[13]魏星,舒乃秋,张霖,等.基于改进PSO-BP 混合算法的电力变压器故障诊断[J].电力自动化设备,2006,26 (5):35-38.
[14]丁玉凤,文劲宇.基于改进PSO 算法的电力系统无功优化研究[J].继电器,2005,33 (6):20-24.
[15]任冲,刘涤尘,潘晓杰,等.与三峡—万县输电线路相连电网的等值简化与实时仿真研究[J].电力科学工程,2006,(1):15-18.
