两级车辆路径问题的多起始点变邻域下降算法

曾正洋，许维胜，徐志宇，倪嘉呈

（同济大学 电子与信息工程学院，上海201804）

随着社会经济的飞速发展和人民生活水平的不断提高，物流活动与日常生活的联系也越来越紧密.物资运输中传统的车辆路径问题（vehicle routing problem，VRP）一般假设单级配送物资，即由中心仓库（depot）直接向需求点（customers）配送物资.但由于物流运输车辆体积大、起步慢，降低了城市道路的通行能力，易加剧城市交通拥堵、噪音和尾气污染，为保护城市环境，很多城市对这类车辆采取限行措施：物资必须首先由大型车辆配送至位于郊区的各个中转站（satellites），再通过小型车辆转运至市内的各个需求点，这就形成两级车辆路径问题（twoechelon vehicle routing problem，2E-VRP［1-6］），如图1所示［7］.图中，s1，s2，s3为中转站，c1，…，c9为 需求点，两级路径用不同的箭头区分.

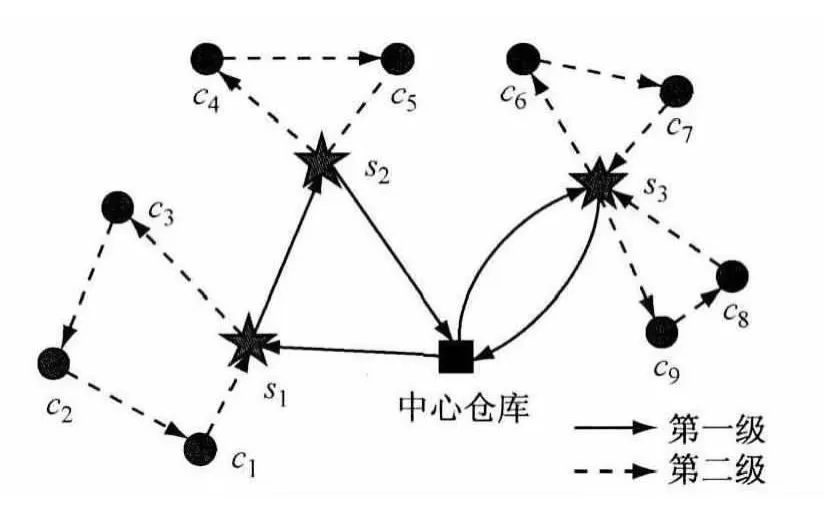
图1 2E-VRP示例Fig.1 An example of 2E-VRP

现有文献对2E-VRP的研究较为有限，求解方法主要分为精确算法和启发式算法两类.Perboli等［1］提出2E-VRP的商品流模型，并采用分支切割精确算法求解，由于计算时间较长，并未给出算法的全部运行时间.Jepsen等［2］提出一种特殊的分支切割精确算法，采用特殊的分支过程来获得可行解.Perboli等［1，3］提出一些有效的不等式，增强对分支切割法中商品流模型的连续松弛.Baldacci等［4］提出了一种新的2E-VRP模型，用于获得有效的下界，然后将2E-VRP解耦为多个带边界约束的多车场车辆路径问题（multi-depot vehicle routing problem，MDVRP）后，再用精确算法求解，求解结果好于已有的精确算法.由于2E-VRP是NP难问题［6］，在问题规模较大时，精确算法求解过程需要相当长的时间.启发式算法有多起始点启发式方法（multi-start［5］）、自适应大邻域搜索（adaptive large neighborhood search，ALNS［6］）算法以及Memetic算法［7］.Crainic［5］首先按与中转站距离将需求点分配至中转站，然后在此基础上搜索改进，由于算法局部开发的程度不足，求解时间较长，且精度较差.ALNS［6］算法用轮盘赌的方法将需求点分配至中转站，再通过扰动―修复―局部搜索的过程持续对当前解进行搜索，该方法求解质量较高，计算速度较快，明显优于Crainic等［5］的多起始点方法，但采用的算子种类、数目过多，实现过程较为复杂.许维胜等［7］设计的Memetic算法将遗传算法与局部搜索合理组合，平衡了求解质量与效率.此外，Crainic等［8］研究了中心仓库、中转站以及需求点之间的相对位置关系对总成本的影响；Crainic等［9］研究了广义的配送成本（固定成本、运作成本、环境成本等）对2E-VRP的中转站布局的影响.

变邻域下降算法（variable neighborhood descent，VND［10-11］）是变邻域搜索算法（variable neighborhood search，VNS［10-11］）的一种.VNS最早于文献［11］中提出，其核心思想为对一组邻域进行系统的切换，一方面通过目标值下降的过程找到局部最优，另一方面通过对该局部最优进行扰动以跳出局部最优，获得新的搜索起始点.VND去除了VNS的扰动过程，虽优化效率较高，但由于缺少扰动过程，易于陷入局部最优.

在求解困难的组合优化问题时，启发式方法需要一定多样性以搜索到全局最优.多起始点方法（multi-start methods［12-13］）在搜索到局部最优时，通过生成全新的初始解进行搜索改进，以增加算法的多样性，避免在改进希望较小的解周围反复无效搜索.多起始点方法的每次迭代均产生一个局部最优值，迭代过程中最好的局部最优值为最终的输出.多起始点方法的局部开发能力需要适当强化.多起始点方法与变邻域下降算法的组合已成功解决旅行维修员问题（traveling repairman problem，TRP［14］）、卡车带拖车路径问题（truck and trailer routing problem，TTRP［15］）、校车路径问题（school bus routing problem，SBRP［16］）等 NP难题，不仅获得了较好的结果，而且由于实现过程较为简单，便于实际应用.由于城市物流优化需要通过易于实现与调整参数的算法快速给出较好的配送方案，受上述研究成果的启发，本文选择合适的局部搜索算子并结合多起始点方法，设计一种易于实现的多起始点变邻域下降算法（multi-start variable neighborhood descent，MS-VND）求解2E-VRP，以达到求解质量和计算时间的平衡，辅助城市物流的优化决策.

1 2E-VRP问题描述

2E-VRP可由节点（中心仓库、中转站、需求点）集合V和边的集合A组成的有向图G来表示［1-6］，G=（V，A）.集合V中包含三类节点：中心仓库V0，ns个中转站组成的集合Vs，以及nc个需求点组成的集合Vc.节点i和节点j之间的距离用D（i，j）表示.每个需求点ci的需求量为Q（ci）.每个需求点只能配送一次，且不允许由中心仓库直接配送.中转站可由第一级车辆多次配送.同级的车辆具有相同的运载容量约束，第一级和第二级的车辆最大容量分别为W1和W2，可用车辆数分别为K1和K2.

由于存在多个中转站和多个需求不可分割的需求点，2E-VRP的第二级可看成一个MDVRP；由于中转站的转运量可能超过第一级车容量W1，进而需要多次配送，故2E-VRP的第一级可看成需求可分割车辆路径问题（split-delivery vehicle routing problem，SDVRP［2］）.2E-VRP首先追求两级使用的车辆数最少，其次两级总配送路径最短.2E-VRP不同于VRP：改变任一需求点所属的中转站可能影响第一级总距离；改变中转站的转运量也可能影响第二级配送方案.由于两级的配送方案之间存在这样相互耦合的关系［2］，因此2E-VRP的求解必须综合考虑两级的配送.

2 多起始点变邻域下降算法

2.1 求解思路

考虑两级问题各自特性，为易于获得初始可行解，自底向上求解2E-VRP［7］.在获得第二级MDVRP的可行配送方案后，计算各个中转站的转运量，据此求解第一级的SDVRP，获得完整的随机初始可行解，然后通过变邻域下降算法改进；当使用的几种局部搜索算子均无法改进时，采用多起始点技术重新生成随机的初始可行解，重复变邻域下降算法的改进过程.到达最大迭代次数后，终止搜索过程，输出已搜索到的最佳配送方案.

2.2 初始可行解的构建

为增加搜索过程的多样性，第二级的初始分配方案通过对由所有需求点构成的随机排列进行合理的分割实现.通过对文献［7，17］的Split算法进行改进，考虑中转站与中心仓库的距离远近，同时以优先考虑车辆数最少，其次总路径长度最短的原则按随机排列中的顺序将需求点合理分配至各个中转站，获得第二级的配送方案.Split算法最早由Beasley［18］提出，由Prins［19］给出了详细的实现过程.基本的Split算法只适用于单车场、单级的VRP，不适用于2E-VRP；文献［7，17］中改进的Split算法虽考虑了多个车场，但只针对单级情形进行讨论，并未拓展至两级情形.除文献［7］外，已有的Split算法只考虑分割距离最短单一目标，并未考虑最小化所使用车辆数.针对当前Split算法求解2E-VRP存在的不足，并综合考虑2E-VRP的中转站—需求点之间以及中心仓库—中转站之间的距离关系，改进文献［7］中的Split算法，改进后算法的流程图如图2所示.

图2中改进的Split算法作用对象为由所有需求点构成的随机排列T，0号点为虚拟的起始点，i为当前搜索起始点，j为以i为起点的可行弧的终点［7］；Ni为排列T中前i个需求点所需要的第二级车辆数，Li为对应的综合成本；为考虑中转站与中心仓库之间的距离，在每条可行弧的成本中增加其所属中转站至中心仓库的距离这一惩罚项，从而获得综合成本.计算完毕后，Nnc为第二级方案所需的车辆数，Si记录了T中第i个需求点所属的中转站，pi记录了以第i个需求点为终点的单条路径的起始节点.利用Pi和Si，逆向复现第二级配送方案［7，17］.

获得第二级初始可行的配送方案后，计算各个中转站的转运量，然后优先处理转运量超过W1的中转站，满载的第一级车辆从中心仓库直接配送这些中转站，同时减少其相应的转运量，直至每个中转站的转运量均小于W1，将第一级的SDVRP转化为VRP［6，20］，处理完毕后转运量大于零的中转站组成第一级的排列，按照贪婪原则分配车辆，并通过局部搜索进一步改进［6-7］，再结合中心仓库与中转站之间的直达路径，得到第一级的配送方案；两级的配送方案相结合，得到2E-VRP完整的初始可行解.

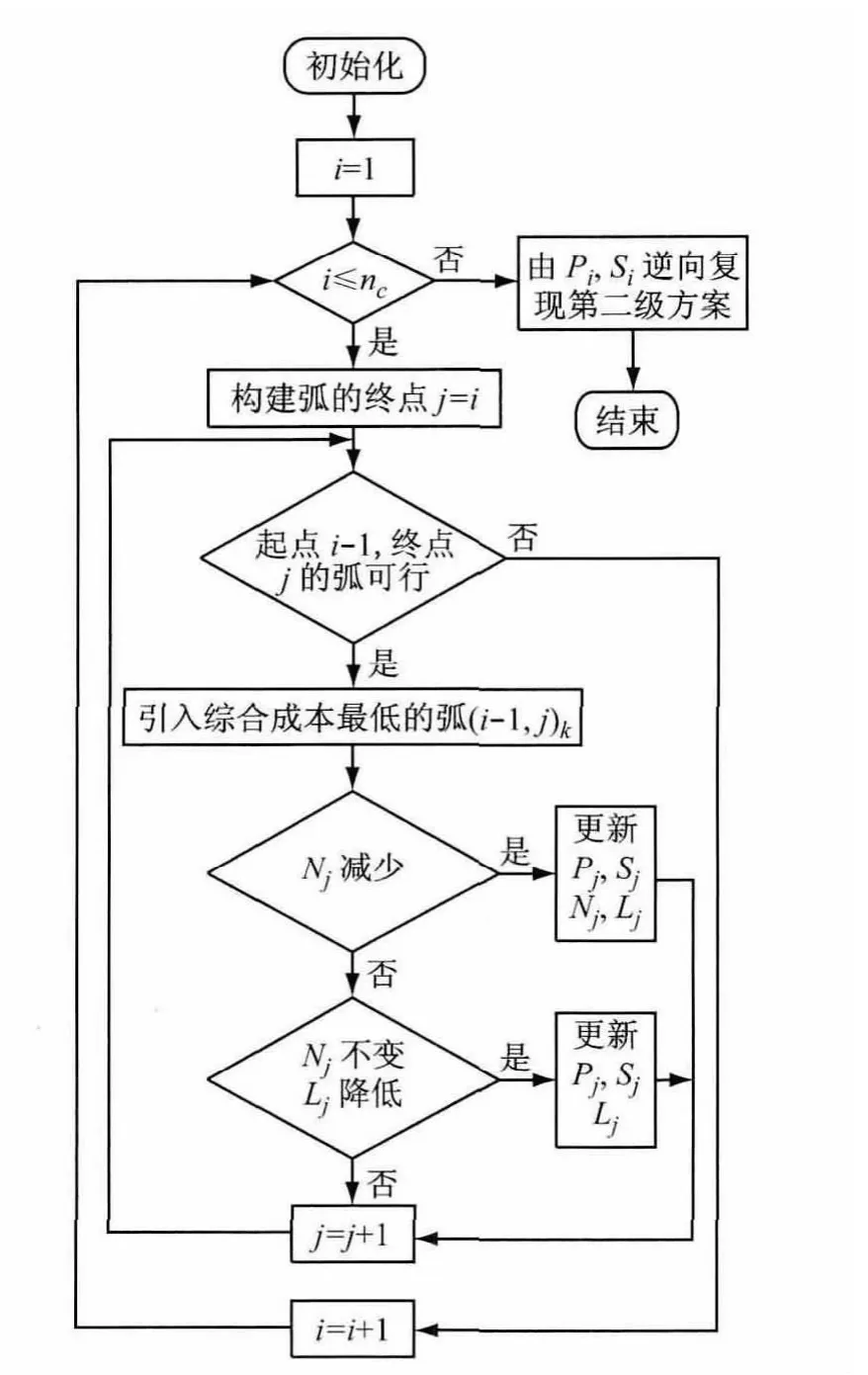
图2 改进的Split算法流程图Fig.2 Flowchart of the improved Split algorithm

2.3 变邻域下降算法中局部搜索算子的选择

局部搜索分别针对第一级和第二级配送方案进行.由于处理后的第一级是一个规模较小的VRP，采用swap和move算子［6］对第一级方案进行搜索改进，限定swap算子交换两个中转站的位置；move算子将一个中转站移动到另一条第一级路径中.第一级的局部搜索仅在计算第一级总距离时执行.

第二级问题规模较大，所使用的局部搜索算子分为路径内部和路径之间两种.第二级路径内部搜索改进采用2-Opt，Intra-swap和Intra-move算子［6］.2-Opt算子通过左右翻转路径内部的一段连续的节点来进行搜索改进；Intra-swap算子将单个节点与单个或连续两个节点交换位置来搜索改进；Intra-move算子将单个或连续两个节点前后移动位置，移动范围包括一条路径的中转站.

第二级路径之间算子采用2-Opt＊、Inter-swap以及Inter-move算子［6］，并针对2E-VRP扩大了Inter-swap和Inter-move算子的搜索范围.2-Opt＊算子分别去除两条第二级路径中的一条边，再重组为两条新路径；Inter-swap算子交换两条第二级路径中的节点，每条路径最多交换三个连续节点；当两条路径分别属于不同的中转站时，Inter-swap算子包含这两条路径所属中转站的交换；Inter-move算子将一条第二级路径中的需求点移动到另一条中，最多允许移动连续三个需求点；此外，Inter-move算子可重新分配单条第二级路径所属的中转站来扩大搜索范围.为增强搜索的效能，当路径之间算子产生的新路径均满足第二级车容量约束时，采用路径内部搜索算子进一步优化［7］.

所有的局部搜索算子均采用First-Accept策略［6-7］以减小计算量：当邻域中搜索到更优解时，立即替换当前解，并继续局部搜索过程.每次生成一个可行的初始解后，局部搜索算子按给定顺序循环执行，直至所有算子均无法获得改进.由于第二级路径内部搜索改进算子执行次数较多，其与路径之间算子结合使用时，仅顺序优化路径之间算子邻域中的可行解；在路径之间算子作用之前，对当前解的每条第二级路径使用路径内部的三种算子循环优化以彻底改进.第二级路径之间搜索时，若两条路径属于相同的中转站，对这两条路径改进时不改变中转站的转运量，故不必计算第一级总距离；若两条路径属于不同的中转站，由于改变了中转站的转运量，则必须进一步计算第一级总距离；Inter-move算子重新分配一条第二级路径所属的中转站时，由于改变了中转站的转运量，也必须进一步计算第一级总距离［7］.

2.4 求解2E-VRP的MS-VND算法流程图

本文的MS-VND算法流程图可用图3简要表述，其中参数i为当前迭代次数，Imax为算法设定的最大迭代次数；Improve指示迭代过程中是否出现改进；判定“Trips可行”是指判定其是否满足第二级可用车辆数约束.“路径内部算子循环优化S”是指对利用2-Opt，Intra-swap和Intra-move三种路径内部搜索算子循环改进当前解S的每条第二级路径.图中第二级路径之间的2-Opt＊，Inter-swap以及Inter-move算子搜索过程已经包含中转站转运量变化时对第一级总距离的重新计算.由于第一级总距离的计算相对简单，且在上述三种算子的执行过程中反复调用，故图3并未突出显示.

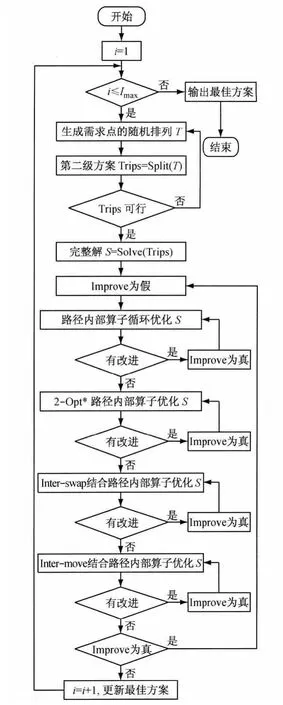
图3 MS-VND算法流程图Fig.3 Flowchart of MS-VND

3 仿真与分析

3.1 算例描述

本文算例取自文献［8］，这些算例包含一个中心仓库、5个中转站以及50个需求点，并采用了不同的需求点分布与中转站位置组合.需求点有随机分布（random）、重心分布（centroids）、象限分布（quadrants）三种分布类型：随机分布中需求点的x，y坐标均服从［0，100］内的均匀分布；重心分布模拟大城市中的市区和郊区，中心40×40的方块代表市中心，市中心外围的4个20×20的方块代表郊区，中心方块中有6个需求点群，而周围每个郊区方块中各有一个需求点群；象限分布模拟围绕河流、主干道、山谷等分布的城镇，需求点集中分布在四个象限内.中转站有三种分布类型：随机分布（random），切片分布（sliced）、禁区限制（forbidden zone）：随机分布表示没有任何限制，中转站可分布在城市周围的任何位置；切片分布是指将城市周围分为ns块，每块随机放置一个中转站；禁区限制模拟需求点靠近海边或者山脉分布的情形，有些地点无法设置中转站，中转站需要设置在这些禁区外.

3.2 实验设置

在主频为2.8GHz的Intel奔腾双核E5500处理器（只使用单核心）、内存为2GB的硬件平台上通过Microsoft Visual C++6.0实现本文求解2EVRP的MS-VND算法.设置最大迭代次数为1 000，为便于和ALNS［6］对比，每个算例均进行了5轮独立的计算.

3.3 实验结果与对比分析

针对18个标准算例的测试结果如表1所示，除时间外，表中的数值均未设定单位，可表示车辆行驶的总里程，也可表示车辆行驶的总时间.ALNS［6］算法在主频为2.2GHz的AMD Opteron CPU上通过C++实现，每个算例均进行5轮的独立计算；MA为Memetic算法［7］在本文的软硬件环境下的测试结果，除5轮独立计算外，均使用文献［7］中原有的参数配置；MS-VND为本文提出的多起始点变邻域下降算法的测试结果.考虑到ALNS算法实现的硬件平台差异，为公平比较算法的时间，从文献［21］中获得两种CPU的性能得分（分别为1 234和1 658），在此基础上对计算时间进行比例缩放［5］：以ALNS算法的计算时间为基准，MA和MS-VND的计算时间在原有基础上乘以1 658再除以1 234.表1中给出了三种算法公平化之后最好结果首次出现的平均时间.表1中，加粗的数值表明MS-VND算法的结果优于其他两种算法，加下划线的数值表明其结果不如其他两种算法.

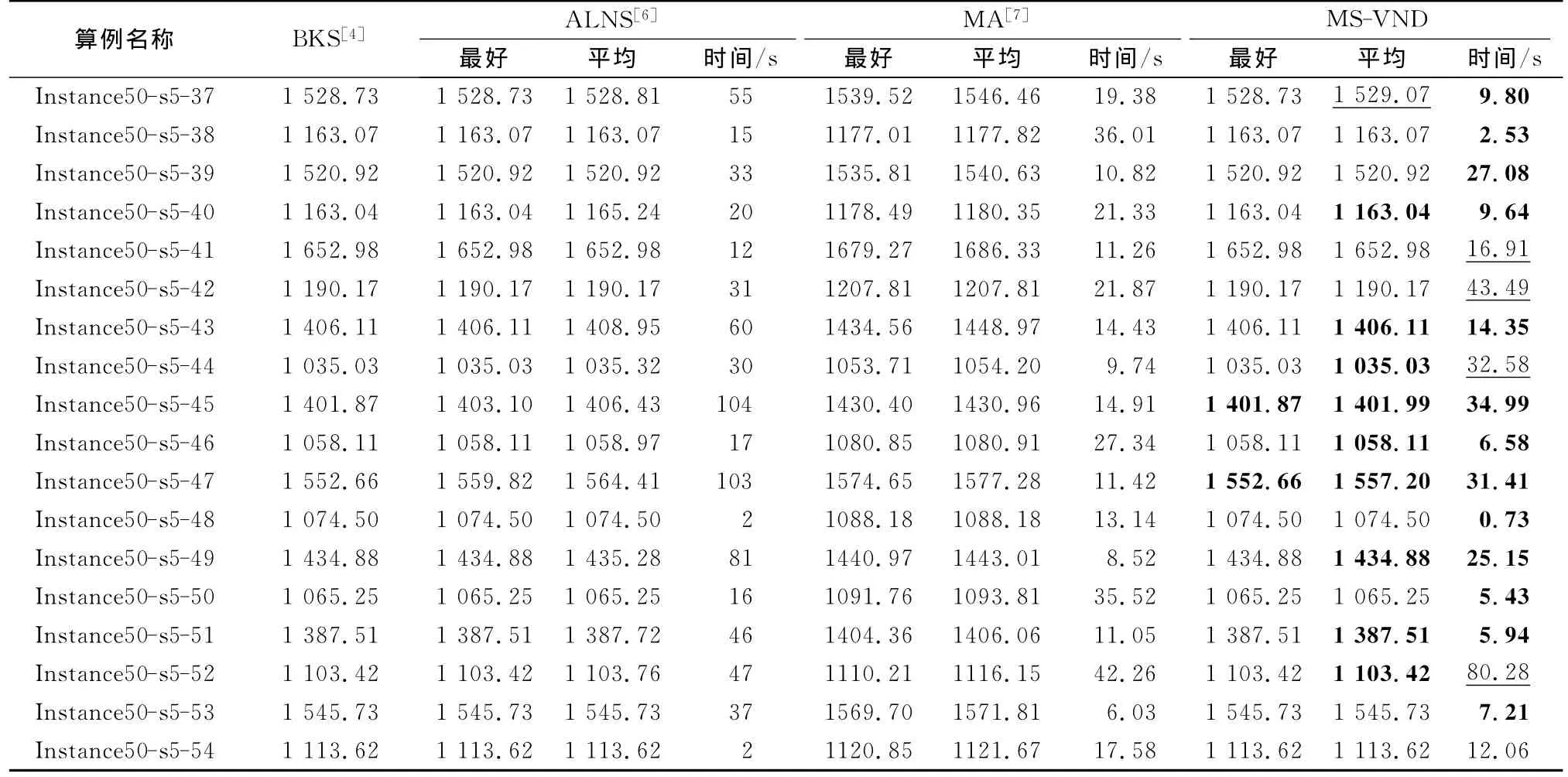
表1 2E-VRP标准算例测试结果比较Tab.1 Computational results comparison for 2E-VRP benchmark instances

表1分别进行了算法求解质量与计算时间的比较分析.MA无论是最好结果还是平均结果都不如ALNS与MS-VND，且差距较为明显，故单独比较ALNS与MS-VND.从算法获得的最好结果来说，MS-VND在每个算例下的最好结果均达到或优于ALNS，特别地，Instance50-s5-45和Instance50-s5-47这两个算例的最好结果优于ALNS；此外，MS-VND均获得了这几个算例当前已知的最好结果［4］.从算法5次独立计算获得的平均结果来说，除了算例Instance50-s5-37的平均值略次于ALNS外，MSVND在其他算例下的运行结果的平均值均达到或优于ALNS算法，且有9个算例的平均值优于ALNS.综合评价计算结果质量，可知MS-VND算法优于ALNS算法与Memetic算法.

从三种算法最好解出现的平均时间考察算法的计算效率.由于三种算法时间均已考虑硬件配置进行公平化处理，故可直接比较.从表1可见，这三种算法的计算时间均不超过2min，较为合理；由于ALNS与MS-VND的计算结果质量明显优于MA，故先比较ALNS与MS-VND的计算时间，MS-VND在5个算例下计算时间慢于ALNS，其余13个算例下计算时间均快于ALNS；ALNS有4个算例的计算时间达到或超过1min，而 MS-VND只有1个.MA的计算时间均在1min之内，计算速度较快，但由其较差的求解质量可知，由于局部开发的程度不够，算法陷入早熟收敛.从计算时间角度看，MSVND优于ALNS算法，且与Memetic算法接近.

再结合算法实现过程与参数调节的难易程度进行比较，ALNS需要实现的算子与需要调节的参数数目均最为复杂，MA其次，而本文的MS-VND只需要实现1种改进的Split算法、6种简单的局部搜索算子，并设置1个最大迭代次数即可，实现过程最为容易，更有利于实际应用.

综合考查算法的结果质量、计算时间以及实现与参数调节的难易程度这几方面的因素，可知本文提出的MS-VND算法优于ALNS算法与Memetic算法，更便于在城市物流优化决策中应用.

4 结论

本文针对城市物流中新出现的两级车辆路径问题（2E-VRP），设计了一种多起始点变邻域下降算法（MS-VND）进行求解，针对2E-VRP改进了已有的Split算法以获得随机的初始可行解，并扩展了VND中几种局部搜索算子的搜索范围.标准算例的实验结果表明，所提算法平衡了求解质量与计算时间，性能优于当前求解2E-VRP最好的两种启发式算法.此外，由于算法的实现过程与参数调节较为简单，在城市物流优化决策过程中更有实际意义.

下一步的工作将结合城市物流的实际情形提出更为精细的模型，并改进本文的算法进行求解.

［1］ Perboli G，Tadei R，Vigo D.The two-echelon capacitated vehicle routing problem：models and math-based heuristics［J］.Transportation Science，2011，45（3）：364.

［2］ Jepsen M，Spoorendonk S，Ropke S.A branch-and-cut algorithm for the symmetric two-echelon capacitated vehicle routing problem［J］.Transportation Science，2013，47（1）：23.

［3］ Perboli G，Tadei R.New families of valid inequalities for the two-echelon vehicle routing problem［J］.Electronic Notes in Discrete Mathematics，2010，36：639.

［4］ Baldacci R，Mingozzi A，Roberti R，etal.An exact algorithm for the two-echelon capacitated vehicle routing problem［J］.Operations Research，2013，61（2）：298.

［5］ Crainic T G，Mancini S，Perboli G，etal.Multi-start heuristics for the two-echelon vehicle routing problem［J］.Lecture Notes in Computer Science，2011，6622：179.

［6］ Hemmelmayr V C，Cordeau J F，Crainic T G.An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics［J］.Computers &Operations Research，2012，39（12）：3215.

［7］ 许维胜，曾正洋，徐志宇.一种求解两级车辆路径问题的Memetic算法［J］.控制与决策，2013，28（10）：1587.XU Weisheng，ZENG Zhengyang，XU Zhiyu.A memetic algorithm for solving the two-echelon vehicle routing problem［J］.Control and Decision，2013，28（10）：1587.

［8］ Crainic T G，Perboli G，Mancini S，etal.The two-echelon vehicle routing problem：a satellite location analysis［J］.Procedia Social and Behavioral Science，2010，2（3）：5944.

［9］ Crainic T G，Mancini S，Perboli G，etal.Impact of generalized travel costs on satellite location in the two-echelon vehicle routing problem［J］.Procedia Social and Behavioral Science，2012，39：195.

［10］ Hansen P， Mladenovic N，Brimberg J，etal.Variable neighborhood search［C］//Handbook of Metaheuristics.New York：Spring Science Business Media，2010：61-86.

［11］ Mladenovic N，Hansen P.Variable neighborhood search［J］.Computers &Operations Research，1997，24（11）：1097.

［12］ MartíR，Moreno-VegaJ M，Duarte A.Advanced multi-start methods［C］//Handbook of Metaheuristics.New York：Spring Science Business Media，2010：265-281.

［13］ MartíR，Resende M G C，Ribeiro C C.Multi-start methods for combinatorial optimization ［J］.European Journal of Operational Research，2013，226（1）：1.

［14］ Salehipour A，Sorensen K，Goos P，etal.Efficient GRASP+VND and GRASP+VNS metaheuristics for the traveling repairman problem ［J］.4OR—A Quarterly Journal of Operations Research，2011，9（2）：189.

［15］ Villegas J G，Prins C，Prodhon C，etal.GRASP/VND and multi-start evolutionary local search for the single truck and trailer routing problem with satellite depots［J］.Engineering Applications of Artificial Intelligence，2010，23（5）：780.

［16］ Schittekat P，Kinable J，Sörensen K，etal.A metaheuristic for the school bus routing problem with bus stop selection［J］.European Journal of Operational Research，2013，229（2）：518.

［17］ Nguyen V P，Prins C，Prodhon C.Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking［J］.European Journal of Operational Research，2012，216（1）：113.

［18］ Beasley J E.Route first-cluster second methods for vehicle routing［J］.Omega，1983，11（4）：403.

［19］ Prins C.A simple and effective evolutionary algorithm for the vehicle routing problem［J］.Computers &Operations Research，2004，31（12）：1985.

［20］ Archetti C，Speranza M G，Hertz A.A tabu search algorithm for the split delivery vehicle routing problem ［J］.Transportation Science，2006，40（1）：64.

［21］ Prins C.CPU benchmarks［EB/OL］.［2014-07-02］.http：//www.cpubenchmark.net/cpu＿list.php.