静电收集-能谱法测氡装置设计

过惠平 魏志浩 吕 宁 吕汶辉 鲍卫红 赵永刚

（第二炮兵工程大学 西安 710025）

静电收集-能谱法测氡装置设计

过惠平 魏志浩 吕 宁 吕汶辉 鲍卫红 赵永刚

（第二炮兵工程大学 西安 710025）

提出静电收集-能谱法测氡原理，初步建立静电收集-能谱法测氡系统。针对影响测量结果的铝箔、空气层等主要因素，建立合理的放射源和几何模型，运用Geant4软件进行模拟，对结果进行处理，得到了α粒子能量大小、α能谱的半高宽(Full Width at Half Maximum, FWHM)、能量分辨率、峰位差、能谱分辨能力与铝箔和空气层厚度的关系，确定了铝箔、空气层厚度最佳取值范围。并选择合适的铝箔、空气层厚度，在氡室内进行测量，验证了模拟分析的正确性，为静电收集-能谱法测氡装置的研制提供了可靠数据。

静电收集，Geant4，氡测量，α能谱，蒙特卡罗

联合国原子辐射效应科学委员会(United Nations Scientific Committee on the Effects of Atomic Radiation, UNSCEAR)在2008年报告中指出，在人类受到的天然辐射源照射中，氡及子体暴露所致年有效剂量约占天然辐射源所致年有效剂量的50%[1]。所以提高测氡仪器的测量水平使氡得到有效防范显得尤为重要。

国内外对氡及氡子体的测量已进行过许多研究，目前常用的测氡方法有电离室法、闪烁室法、双滤膜法、积分计数法、活性炭浓缩法、径迹蚀刻法以及静电扩散法等[2]。但众多方法都存在优缺点，总结起来分为两类：一类是在线测量方法，这类方法能够进行实时测量，但一般只能进行计数测量，反映氡及子体的信息量较少；另一类是能谱测量方法，这类方法能够测量能谱，可反映出氡及子体的大量信息，但是一般只能进行离线测量。

针对氡及子体测量方法的优缺点，本文提出了静电收集-能谱测氡方法。基于α谱仪系统，采用静电收集原理构造探头，实现了具有能量区分本领的氡及氡子体浓度在线实时分析测量功能。

1 静电收集-能谱法测氡原理及系统构成

自然界中，氡主要有三种天然放射性同位素，即219Rn、220Rn、222Rn，它们分别来源于铀系、钍系和锕系三大天然放射系。由于219Rn、220Rn的半衰期很短，分别为3.96 s、55.6 s，所以219Rn、220Rn在大气中含量相对很少；而222Rn的半衰期(3.823 d)比较长，大气中的氡主要以222Rn存在，因此氡的测量通常是222Rn及其子体的测量[2]。

1.1静电收集-能谱法测氡原理

静电收集-能谱法测氡原理如图1所示，在浓度差作用下，室外氡气体经扩散透过滤膜进入收集室，而室外已衰变的氡子体固体颗粒被阻挡在收集室外，达到平衡后，室内外氡浓度几乎相等；收集室内，氡衰变产生的214Po、218Po等子体90%以上带正电，氡子体在收集室加电后产生的电场作用下被收集到探测器表面的铝箔上，其衰变产生的α粒子穿过铝箔被探测器接受，经多道分析器处理形成能谱。

图1 静电收集-能谱法测氡系统结构图Fig.1 Structure illustration of radon measuring system with electrostatic collection-energy spectrum method.

1.2静电收集-能谱法测氡装置系统构成

该测量系统由氡室、BH1324C型单路α谱仪、探头部分和计算机等部分组成，其装置如图2。

静电收集-能谱法测氡装置主要是对探头部分的设计。探头部分分为收集室和金硅面垒半导体探测器两个模块。收集室是桶状结构，由金属丝网构成，其外表面覆有一层用于过滤空气中的固体杂质和氡衰变子体的滤膜；金硅面垒半导体探测器固定于收集室内顶部中央位置，用于探测被收集到的氡子体衰变产生的α粒子；金硅面垒半导体探测器表面前盖有一薄铝箔，一方面作为收集室加电后的负极，收集室内氡子体；另一方面作为金硅面垒半导体探测器表面的保护层，防止探测器被污染。金硅面垒半导体探测器α能谱系统，用于放大、处理核信号，最终形成能谱。

图2 静电收集-能谱法测氡系统构成图Fig.2 Structure of radon measuring system with electrostatic collection-energy spectrum method.

2 探头部分模拟设计

能谱法在线连续测氡装置中，BH1324C型单路α谱仪、计算机是成型产品，可靠性比较高，影响能谱测量准确性的主要是探头部分。探头部分由收集室、金硅面垒半导体探测器、空气层、铝箔组成。在进行氡的α能谱测量时，铝箔表面的氡子体衰变产生α粒子，穿过铝箔和空气层被金硅面垒半导体探测器探测到，不同厚度的铝箔、空气层对α粒子能量大小、α能谱的半高宽(Full Width at Half Maximum, FWHM)、峰位差、能量分辨率等影响很大。为使α粒子能量的损耗具有一致性，保持能量的线性关系，对探头部分进行分析，建立合理的α放射源模型，设计几何结构，利用Geant4软件，选择合适的物理过程进行模拟，并对数据进行处理。得到了不同厚度的铝箔、空气层与α粒子能量大小、α能谱的半高宽、峰位差、能量分辨率等之间的关系，初步研究探头部分铝箔、空气层厚度对能谱测量的影响，确定铝箔和空气层厚度范围。

2.1放射源模型

空气中存在的主要氡的放射性同位素222Rn、220Rn、219Rn中，220Rn、219Rn的半衰期很短，且空气中含量很少，对氡的α能谱测量的影响可以不予考虑。因此，只考虑由222Rn衰变产生的氡子体的测量即可。表1是铀系衰变链中222Rn及其子体的衰变产生的能量及半衰期[3]。

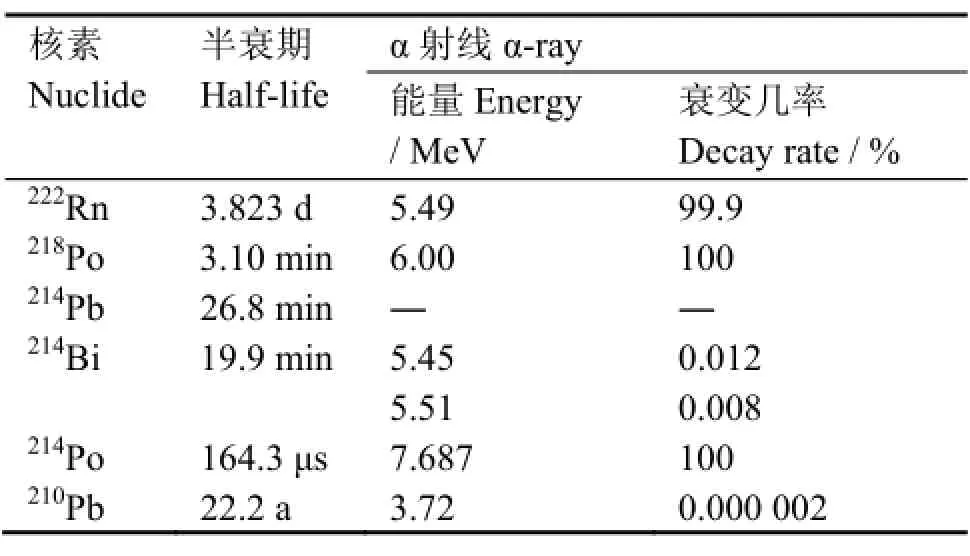
表1 铀系222Rn及子体衰变表Table 1 Decay table of 222Rn and 222Rn daughters in uranium series.

在铀系中，222Rn 及子体衰变产生的β、γ射线的能量和衰变几率都比较低，对α能谱的测量影响不考虑[4]；由表1可以看出，222Rn发生α衰变产生α粒子能量为5.49 MeV，但由于222Rn为气态原子，不带电，222Rn均匀分布在收集室内，且5.49 MeV的α粒子在空气中的射程只有3.82 cm[4]，所以探测222Rn衰变产生的α粒子效率很低，对α能谱测量影响可忽略；214Bi的α衰变几率很低，约为0.033%，其影响可忽略；210Pb的半衰期很长，为2.22 a，且衰变几率极低，210Pb及其衰变子体的α粒子的影响可忽略；218Po、214Po的半衰期比较短，衰变几率均为100%，其能量分别为6.00 MeV、7.687 MeV，且在其能量附近没有其它核素干扰，采用α能谱法测量的α能谱主要是这两种核素的贡献。

静电收集-能谱法测氡实质是对沉积在铝箔表面的氡子体218Po、214Po的α能谱测量，所以可将模型等效为半径等于铝箔半径的面源，其发射能量为6.00 MeV、7.687 MeV，平衡条件下发射几率分别为50%。

2.2探头几何结构

为研究铝箔对不同能量α粒子的阻挡关系，将氡探头抽象为如图3所示模型。该模型由等效面源、铝箔、空气层和探测区等部分组成。其中，面源为发射6.00 MeV和7.687 MeV能量的α粒子，发射几率分别为50%，半径为10 mm的圆柱体，覆盖在铝箔表面；铝箔是半径为10 mm、厚度为dl的圆柱体，变化范围取0.0013-0.0260 mm（区分度为0.0013mm）；探测区与铝箔之间为空气层，其半径为10 mm，厚度为dk，变化范围取0.5-1.5 mm（区分度为0.1 mm）。

图3 模型结构示意图Fig.3 Schematic diagram of model structure.

模拟采用Geant4 9.6版本，调用其物理库中的LHEP为物理过程，通过改变铝箔、空气层厚度，计算由面源发射的6.00 MeV和7.687 MeV能量的α粒子穿过铝箔、空气层后的能谱及相关参数。

3 模拟结果分析及验证

3.1模拟结果

根据所建物理模型，在Linux环境下，编写用户文件，经模拟计算[4-5]得到不同能量的α粒子穿过不同厚度铝箔、空气层的相关数据，其α能谱如图4所示（讨论各个参数与不同厚度铝箔、空气层关系时，只选取了部分参考点）。

由图4看出，当空气层厚度一定时，随着铝箔厚度的增加，α能谱展宽变大，峰值降低，能量损失越来越严重；当铝箔厚度一定时，随着空气层厚度的增加峰值略有衰减，但其变化不大。

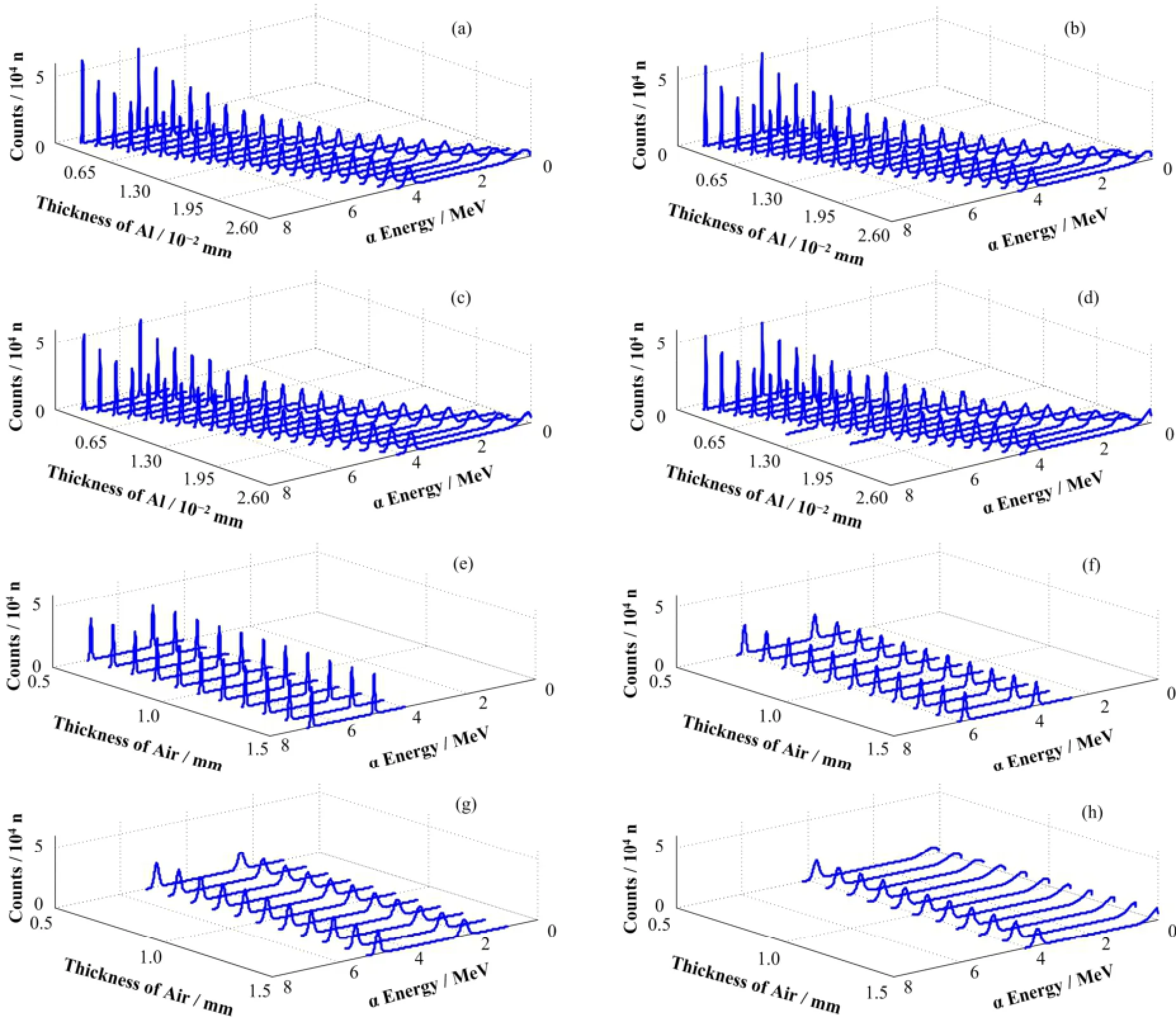
图4 穿过不同厚度铝箔、空气层的α能谱(a) 0.6 mm厚空气层，(b) 0.9 mm厚空气层，(c) 1.2 mm厚空气层，(d) 1.5 mm厚空气层，(e) 0.006 5 mm厚铝箔，(f) 0.013 mm厚铝箔，(g) 0.019 5 mm厚铝箔，(h) 0.026 mm厚铝箔Fig.4 Spectrum of α particles passed through different thickness of aluminum foil and air layer. (a) Thickness of 0.6-mm air layer, (b) Thickness of 0.9-mm air layer, (c) Thickness of 1.2-mm air layer, (d) Thickness of 1.5-mm air layer, (e) Thickness of 0.006 5-mm aluminum foil, (f) Thickness of 0.013-mm aluminum foil, (g) Thickness of 0.019 5-mm aluminum foil, (h) Thickness of 0.026-mm aluminum foil

3.2结果分析

3.2.1 不同厚度的铝箔、空气层与半高宽之间关系分别改变铝箔厚度dl和空气层厚度dk，得到6.00 MeV和7.687 MeV能谱半高宽变化趋势如图5所示。

图5 铝箔厚度(a)、空气层厚度(b)与半高宽关系Fig.5 Relations between FWHM and aluminum foil thickness (a), air layer thickness (b).

由图5可得：

(1) 随着铝箔厚度的增加，能量展宽即半高宽越来越大；随着空气层厚度的增加，能量展宽即半高宽变化不大（当铝箔厚度dl=20×0.001 3 mm时，低能峰已不完整，所以不考虑）。

(2) 当空气层厚度一定时，若铝箔厚度dl≤5×0.001 3 mm，两曲线几乎重合，说明铝箔较薄时铝箔对α粒子作用与能量大小无明显关系；若铝箔厚度dl＞5×0.001 3 mm，低能α粒子的半高宽曲线斜率较大，说明铝箔较厚时，铝箔对低能α粒子作用较为明显。

(3) 当铝箔厚度一定时，空气层厚度对能量展宽即半高宽影响很小，空气层厚度dk在0.5-1.5 mm内，半高宽略有增大，但其变化不大。

3.2.2 不同厚度的铝箔、空气层与能量分辨率关系

分别改变铝箔厚度dl和空气层厚度dk，得到6.00 MeV和7.687 MeV的α能谱的能量分辨率变化趋势如图6所示。

图6 铝箔厚度(a)、空气层厚度(b)与能量分辨率关系Fig.6 Relations between energy resolution and aluminum foil thickness (a), air layer thickness (b).

由图6可得，当铝箔厚度dl≤10×0.001 3 mm时，6.00 MeV和7.687 MeV的α粒子的能量分辨率相差不大，且随着铝箔厚度的增加，α粒子的能量分辨率变化不大；当铝箔厚度dl＞10×0.001 3 mm时，随着铝箔厚度的增加，能量分辨率逐渐变大，即能量分辨本领逐渐变差，且低能α粒子的这种变化更为明显；当铝箔厚度一定时，随着空气层厚度的增加，峰位差变化不大。

3.2.3 不同厚度的铝箔、空气层与峰位差关系

分别改变铝箔厚度dl和空气层厚度dk，得到α粒子峰位差变化趋势如图7所示。

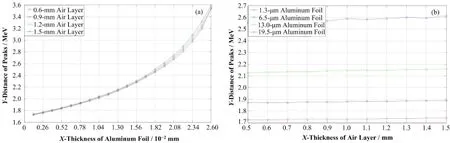
图7 铝箔厚度(a)、空气层厚度(b)与峰位差关系Fig.7 Relations between distance of peaks and aluminum foil thickness (a), air layer thickness (b).

由图7可得，当空气层厚度不变时，随着铝箔厚度的增加，峰位差逐渐变大；当铝箔厚度一定时，若空气层厚度dk≤0.8 mm，随空气层厚度的增加，峰位差几乎没有变化；若空气层厚度dk＞0.8 mm，随空气层厚度的增加，峰位差略有增大，但变化范围很小。

3.2.4 不同厚度的铝箔、空气层与能谱分辨能力

由以上分析可知，两能量的半高宽都随着铝箔和空气层厚度增大，α粒子能量随着铝箔和空气层厚度的增加而减少，而峰位差也随着铝箔和空气层厚度增大，说明两能峰并不一定因为铝箔厚度增大而难以分辨。若要定量地判断两能峰能否可以被分辩，可定义能谱分辨能力η：

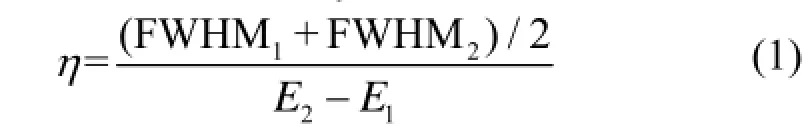
式中，FWHM1、FWHM2分别是两个峰的半高宽；E1、E2分别是两个峰的峰位值。

当能谱分辨能力等于1时，恰好能分辨出两相邻α能峰；当能谱分辨能力小于1时，能很好地分辨出两相邻α能峰，其值越小，能谱分辨能力越好；当能谱分辨能力大于1时，不能分辨出两相邻α能峰，两能峰重叠，形成和峰。

由图8可得，当空气层厚度一定时，随着铝箔厚度的增加，能谱分辨能力逐渐变差，且能谱分辨能力均小于1，即随着铝箔厚度的增加，两能峰越来越近，但仍可以分辩；当铝箔厚度一定时，特别是铝箔较薄时，若空气层厚度dk≤0.8 mm，能谱分辨能力较为稳定；若空气层厚度dk＞0.8 mm，随空气层厚度的变化能谱分辨能力略有增大。

图8 铝箔厚度(a)、空气层厚度(b)与能谱分辨能力关系Fig.8 Relations between energy distinguishing capacity and aluminum foil thickness (a), air layer thickness (b).

综上分析，为使α粒子能量的损耗具有一致性，保持能量的线性关系，结合加工工艺技术，铝箔厚度在0.001 3-0.006 5 mm，空气层厚度在0.5-0.8 mm最佳。

3.3结果验证

为验证仿真结果的正确性，设定铝箔厚度为0.002 6 mm，空气层厚度为0.8 mm，初步搭建静电收集-能谱法测氡实验装置，并在小型氡室[6]内进行测量。选择静电收集场电压为750 V，金硅面垒半导体探测器偏压为60 V，采集时间为13333s，其测量结果如图9所示。

由图9可以看出，在氡室内所测得的α能谱中，主要由两个能峰组成，道址分别为529、629，半高宽分别为27.5、22.7，则计算能谱分辨能力为0.215，其值远小于1，两峰能很好地被分辨出来，从而验证了模拟结果的正确性。

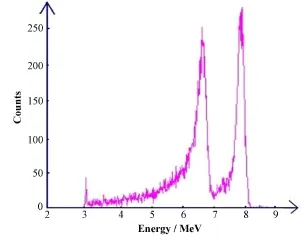
图9 氡室内实测α能谱图Fig.9 α spectrum detected for radon chamber.

4 结语

本研究提出了静电收集-能谱法测氡方法，根据此原理初步搭建了静电收集-能谱法测氡系统。针对静电收集-能谱法测氡装置的主要影响因素，建立了合理的放射源和几何模型，运用Geant4进行模拟，得到了α粒子能量大小、α能谱的半高宽、峰位差、能量分辨率、能谱分辨能力与铝箔、空气层厚度的关系，确定了铝箔、空气层厚度最佳取值范围，分别为0.001 3-0.006 5 mm、0.5-0.8 mm。并选择合适的铝箔、空气层厚度，搭建实验平台，在氡室内进行静电收集-能谱法氡的α能谱测量，验证了模拟分析的正确性。

1 UNSCEAR. Sources and effects of ionizing radiation[R]. United Nations, New York: The General Assembly with Scientific Annexes, 2010

2 张智慧. 空气中氡及其子体的测量方法[M]. 北京: 原子能出版社, 1994: 1-2

ZHANG Zhihui. Methods and applications of radon[M]. Beijing: Atomic Energy Press, 1994: 1-2

3 汲长松. 核辐射探测器及其实验技术手册[M]. 北京:原子能出版社, 2010: 27-28

JI Changsong. Handbook of nuclear radiation detectors & experiment techniques[M]. Beijing: Atomic Energy Press, 2010: 27-28

4 Geant4 user's guide for application developers[EB/OL]. http://geant4.web.cern.ch/geant4/support/userdocuments.s html, 2012-11-30

5 Physics reference manual[EB/OL]. http://geant4.web.cern. ch/geant4/support/userdocuments.shtml, 2012-11-30

6 过惠平, 于洪伟, 尚爱国, 等. 氡测量刻度装置的设计与实现[J]. 原子能科学与技术, 2006, 40(增刊): 130-133

GUO Huiping, YU Hongwei, SHANG Aiguo, et al. Design and realization of calibration apparatus for measuring concentration of radon[J]. Atomic Energy Science and Technology, 2006, 40(Suppl): 130-133

CLCTL817

Design of energy spectrum device for radon measuring with electrostatic collection method

GUO Huiping WEI Zhihao LYU Ning LYU Wenhui BAO Weihong ZHAO Yonggang
(The Second Artillery Engineering University, Xi’an 710025, China)

Background:This research is to take energy spectrum of α particle into consideration in the measurement of radon. Purpose: We aim to find the influence factors of screening particle energy during the process of detector design. Methods: Based on the electrostatic collection radon measurement method, in order to study the influence factors of the measurement such as aluminum foil and air layer, the reasonable radiation source and geometric model are abstracted and calculated with Geant4 software. Results: The best ranges of aluminum foil thickness and air layer thickness are obtained by analyzing their relationship with α energy, the Full Width at Half Maximum (FWHM), the energy resolution, the distance of peaks and the peaks screening power. Conclusion: With the results adopted above, the energy spectrum device is fabricated. Based on the α energy spectrum sampled in a radon chamber, the validity of this design has been proved. It provides a set of reliable data for the design of radon measuring device with electrostatic collection method.

Electrostatic collection, Geant4, Radon measurement, α spectrum, Monte Carlo

TL817

10.11889/j.0253-3219.2014.hjs.37.060206

过惠平，男，1962年出生，2008年于第二炮兵工程大学获博士学位，教授，核辐射监测与防护专业

吕宁，E-mail: lvning1108@aliyun.com

2013-08-21，

2014-03-06