基于最大功率传输若干问题的探讨

蔡文君

基于最大功率传输若干问题的探讨

蔡文君

（西安铁路职业技术学院,710014）

最大功率传输定理是电路理论教学中不可缺少的内容。在电路教学过程中, 本文从一个实例仿真分析了负载获得最大功率的应用条件和效率问题.讨论了当电源电压、内阻可变时不能套用最大功率传输条件及最大功率值的求法，并用仿真软件验证了分析结果。

最大功率传输;使用条件;最大功率值的解法;传输效率

在电子通信工程中，由于信号微弱，通常要求从信号源处获得最大功率，需分析负载在什么条件下可获得最大功率及最大功率为多大，这就是最大功率传输问题。它是电路理论教学中一个很重要的定理。但在教学过程中，负载获得最大功率的应用条件是通过其对负载阻抗一阶导数等于零这个方面得出的。分析的结果显示传输效率很低，只有50%。为什么负载获得最大功率为什么不是效率最高？这对于高职学生的理解和把握来说，不够直观。同时，由于使用条件的描述不具体，学生在应用时直接套用公式，引起定理的误用。本文就最大功率传输定理的理解、使用条件、最大功率值的求法和传输效率进行探讨。

1 最大功率传输原理实例体现

电路如图1所示：在电源US=12V，是电源的内阻，改变负载参数，测量并分析计算电路物理量。数据表：

2 最大功率传输原理适用条件：是用于线性有源二端网络的给定，负载电阻可调的情况

最大功率传输问题是戴维宁定理和诺顿定理最典型的应用，无论正弦交流电路还是直流电阻电路都将把此类问题由图2（）转化为图2（）中负载何时获得最大功率的问题研究。

但在教学过程中，若是负载电阻给定，线性有源二端网络的内部参数可调来使端口负载获得最大功率的情况。学生往往还是套用最大功率传输条件来解决问题。

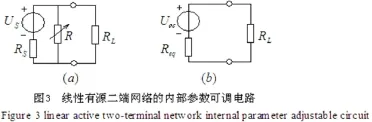
3 负载电阻给定，线性有源二端网络的内部参数可调来使端口负载获得最大功率的方法

那么对于若是负载电阻给定，线性有源二端网络的内部参数可调来使端口负载获得最大功率的情况下，通过戴维南定理得出的和的值都不确定，与内部参数有关,此时负载获得最大功率的条件,一般情况下可根据负载功率的表达式，对可变参数进行一阶导数和二阶导数的方法确定出函数的极值， 如果变量不止一个, 应利用多元函数求极值或最值的方法来求出最大功率传输条件和最大功率值。

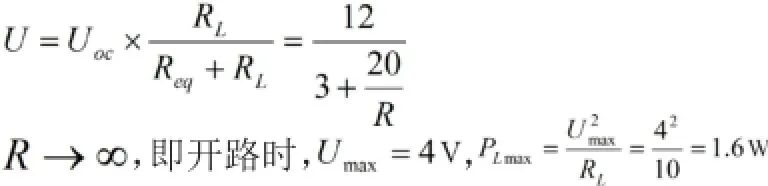
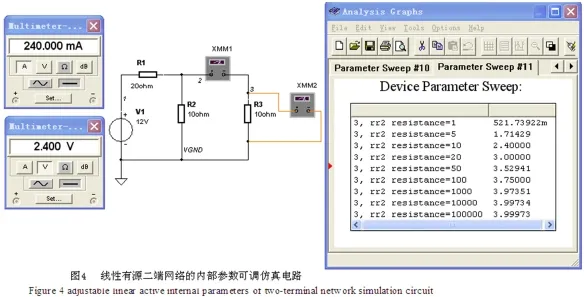
利用Multisim2001软件，进行参数扫描分析结果相同，如图4中：

4 最大功率传输时电源的效率分析

但对于12V电压源的发出功率为：

Based on Several Issues of the Maximum Power Transmission

Cai Wenjun
(Xi'an Institute of Railway Technology,710014)

The maximum power transfer theorem is an important part of electric circuit theory.In the process of circuit teaching,this article obtained from an instance simulation analysis of the load application conditions of the maximum power and efficiency,.Discuss when the power supply voltage,internal resistance variable cannot be applied maximum power transfer condition and the method to get maximum power value, using the simulation software to verify the analysis results.

Maximum power transfer ；Conditions of use；Algorithms for the maximum power value；Transmission efficiency