电动汽车充电站最优规模和布局

王泽黎，齐 灿

(华北电力大学电气与电子工程学院，北京市102206)

0 引 言

为减少雾霾天气、降低PM2.5 浓度，发展节能、环保的交通工具越来越成为各界关注的焦点［1］。在此背景下，电动汽车产业得到飞速发展，销售市场已初具规模。但是，对于电动汽车采用充电还是换电模式补充能量，国内外一直争议不断。国家电网公司和南方电网公司推荐换电池为主的电动汽车运营方案，制定电动汽车电池充电站的最优规划迫在眉睫。

基于电池租赁的换电池模式有如下优点:(1)电池由电网公司或专业租赁公司购买，消费者只需要交纳租赁价格，成本大降，激发用户购车积极性;(2)换电池有利于统一规范电池标准以及实现电池生产、管理、运输、维护等过程的规模效益;(3)电池更换既能保证电能迅速补给又不会损害电池，有利于延长电池的使用寿命［2］;(4)电池充电站在满足用户对充电电池需求的同时，也可以协助电网实现“削峰填谷”，提高负荷利用率。

文献［3］根据地理因素和充电站服务半径确定候选站址，同时以充电站的投资、运行成本和网损费用之和最小为目标，构造电动汽车充电站规划的最优数学模型，并采用改进的原对偶内点求解。文献［4］将充电者的充电时间限制在1个硬时间窗内，以充电站投资者投入成本最小为目标，建立了计及充电路径选择、充电电价的充电站规模选择和布局的最优模型，以满足不同地点电动汽车动态充电需求。文献［5］引入了对电动汽车分层、分区调度的理念，通过优化各电动汽车代理商在各时段对充电负荷和放电出力的调度，使系统在目标时间区间内总负荷水平的方差最小，建立了基于双层优化的可入网电动汽车充放电调度模型。文献［6］对电动汽车充电的负荷特性进行分析，在简化锂电池I－U 充电模型的基础上，得到单个电动汽车的充电模型，提出2 阶段泊松分布的电动汽车充电站集聚模型和基于充电站日充电负荷曲线的电动汽车充电站负荷集聚模型的建模方法。

本文将网络损耗和电力线路建设费用引入电池充电站投资模型，建立一种考虑电动汽车时间－空间分布、电能损耗和新建线路费用的电动汽车电池充电站选址定容新模型。模型用高峰期的交通状况模拟电动汽车，最大程度地满足用户需求。在线路传输功率、无功补偿上下限、站内电池数量和服务半径的约束下，由新建站初始投资、网损费用、新建线路费用和行驶耗电成本构成目标函数。针对建立的模型，采用混沌粒子群优化算法优化充电站布局。

1 电池充电站的经济性模型

电池充电站规划取决于其投资周期费用和用户便利性。投资周期费用是指从开始考虑建设电池充电站，到电池充电站投入正常使用整个过程的费用;用户便利性以用户在电池充电站的等待时间和用户到电池充电站的路程耗时最短为目标。等待时间最短意味着电池充电站的数量、位置和规模都能满足用户更换电池最高峰时刻的需求，减少甚至消除用户排队概率;排除交通拥堵和道路维修等不确定因素的影响，行驶耗时与路程一一对应，行驶路程越长，路上耗时越长，反之亦然。因此，路上行驶距离折算到耗电成本即可以作为衡量用户便利性的指标。本研究以最小化电池充电站投资费用及行驶耗电成本为目标，确定电池充电站的规模、位置、服务范围及用户换电耗时，其数学模型为

式中:G 为电池充电站年费用;Gbj为电池充电站j 的投资成本;Gcj为用户到电池充电站j 的行驶耗电成本，j=1，2，3…，n 分别表示电池充电站的序号;Gbij为电池充电站j 的第i 类投资成本，i 的取值为1，2，3 时分别表示电池充电站初始投资成本、网损成本、新建线路成本。

1.1 投资成本

1.1.1 初始投资成本

新建站j 的初始投资成本Gb1j包括购买设备的费用Ej和购地费用Aj。Ej包括交流充电桩、分箱充电机、电池更换系统、配电监控、充电监控、计费系统及应急充电机等设备购买费用，设备的个数和容量与该电池充电站的规模有关。Aj由电池充电站的位置和占地面积决定。Gb1j的计算公式为

式中:r0表示投资回收率;m 表示电池充电站的运行年限。

1.1.2 网损费用

网损费用Gb2j是指新建电池充电站j 接入原有电网后，新增网络损耗引起的费用。该费用与电池充电站接入电网的位置有关，是衡量电池充电站选址对电网经济性影响的指标之一。Gb2j的计算公式为

式中:rL表示网损费用的年值折算系数;ΔAj表示新建电池充电站j 接入原有电网后的网损增加量。

1.1.3 新建线路费用

新建线路费用Gb3j是指新建电池充电站j 到距离最近的变电站的线路投资，该费用不仅与电池充电站位置有关而且与规划区域电力负荷级别有关。Gb3j的计算公式为

式中:λ1表示单位长度双回线路的投资费用;lj表示电池充电站j 到距离最近的变电站的线路长度。

1.2 行驶耗电成本

行驶耗电成本Gcj的计算公式为

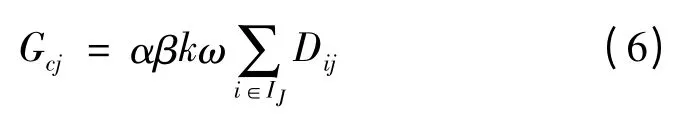
式中:α 表示道路曲折系数;β 表示道路畅通系数;k 表示平均每辆车的充电次数;ω 表示距离对电价的折算系数;Dij表示第i 辆电动汽车到电池充电站j 的直线距离;Ij表示到电池充电站j 换电池的电动汽车集合。

1.3 约束条件

为了避免影响原有电网的安全性、电能质量和满足用户需求，电池充电站规划模型还需加入以下约束条件:

(1)电池充电站线路传输功率约束。

式中:Pj(t)表示电池充电站j 和变电站之间的连接线路在t 时段的传输功率;Pjmax(t)表示电池充电站j和变电站之间的连接线路在t 时段的最大传输功率。

(2)无功补偿上下限约束。

式中:Qj表示电池充电站j 的无功补偿功率;Qjmax和Qjmin分别表示电池充电站j 的无功补偿功率上、下限。

(3)电池数量约束。

式中:nj表示电池充电站j 的电池更换系统单位小时服务电池数量;Tj表示电池充电站j 的日平均工作时间;Nj表示电池充电站j 的充电电池数量。

(4)服务半径约束。

式中:rj表示第j个电池充电站的服务半径;esoc表示电动汽车的平均荷电状态;LN表示电动汽车单次额定行驶里程。

2 混沌粒子群算法

粒子群优化(particle swarm optimization，PSO)算法模拟鸟群觅食行为的一种通过迭代实现的矩阵随机搜索算法［7］。粒子更新自己的速度和位置的公式为:

式中:c1、c2为学习因子;w 为惯性权重;为第k次循环中粒子的位置;为第k次循环中粒子的速度;为粒子的全局最优坐标;xg，j为粒子的局部最优坐标。PSO 算法使用了速度－位置同时搜索的模型，全局寻优速度和能力较强;但基本PSO 算法存在搜索结果精度不高、容易陷入局部解的缺点。为克服这些不足，将混沌运动引入粒子群优化算法，利用混沌运动的遍历性、随机性等特点，当粒子陷入早熟收敛时，用混沌扰动来跳出局部最优，并快速搜寻到最优解，提高解的精度和收敛速度。根据“多点随机全局搜索策略+面向问题的局部寻优算法=最有效的全局优化算法”［8］，运用基于混沌序列的粒子群优化(chaos particle swarm optimization，CPSO)算法，得到理想结果。

混沌运动的数学过程可描述为:对于一个随机初始向量的N 维向量，x0=［x0，1，x0，2，…，x0，N］T，x0，n∈［0，1］，根据某种产生混沌序列的模型，开始迭代。根据参考文献［9］，本文采用逻辑自映射函数，得到迭代序列xm，n。其数学表达式为

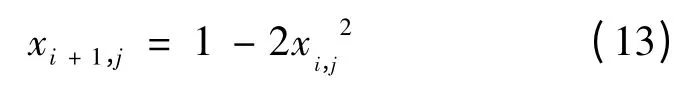
式中:i=0，1，2…，M;j=0，1，…，N。

混沌运动的步骤为:

(1)根据式(13)，在［－1，1］内随机初始化，生成1个N×2 的矩阵;

(2)根据下式将混沌运动的变量映射成种群粒子;

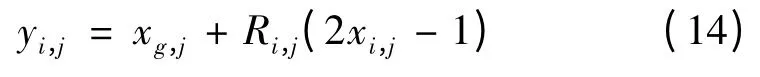
混沌变量xi，j变换到以粒子当前全局最优位置xg，j为圆心，Ri，j为半径的圆上。Ri，j为各邻域内混沌运动的半径，所以通过逻辑自映射函数优化后的种群粒子yi，j的取值范围如下:

(3)计算目标函数的适应值f(xm，n)，并更新全局最优适应值和全局最优位置，更新在混沌迭代过程中的历史最优适应值f(gbest)和历史最优位置xibest。如果混沌迭代后的全局最优适应值优于历史全局最优适应Gbest，则用混沌迭代后的位置和速度替换原有的历史最优位置和速度。其中，速度计算公式为

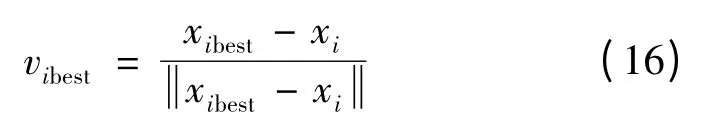
综上所述，基于CPSO 算法的电池充电站规划流程图如图1 所示。

图1 基于CPSO 算法的电池充电站规划流程Fig.1 Planning process of charging station based on CPSO

需要说明的是:

(1)Ni表示满足规划区用户需求时，建设规模为i 的充电站数量，Nmax表示充电站最大需求数量;Ni的计算公式为

式中:Cmax表示1 天内最大充电需求时刻电动汽车的数目;α1表示同时工作的充电站比例;α2表示充电机的同时率;β 表示充电机的充电效率;cosφ 表示功率因数;根据《国家电网公司电动汽车充电设施建设指导意见》，将电动汽车充电站按服务能力分成不同等级，i=1、2、3;li表示等级为i 的充电站的服务能力。

(2)判定粒子运动是否停滞的标准为

式中:δ，NC为根据实际情况设定的常数;NΔG的初始值设为0。当不满足ΔGi＜δ 时，NΔG=NΔG+1，如果不满足式(18)，则判定粒子运动停滞，重新进入混沌运动过程。

3 算例分析

某小区总面积为70.3 km2，常住人口10.7 万人，东西跨度11.06 km，南北跨度9.12 km;该小区主干道2条，次干道4条，支路20条，被主干道划分为4个分区;日均车流总量1.9 万辆。该小区的工业和旅游业发达，电动公交车和出租车占电动汽车总量的比重较大，具体基础数据如表1 所示，电动汽车的位置重心和数量见附表。该小区的居民住宅、旅游区、商业区集中，各用地类型的地价如表2，不同规模的充电站设备的详细配置如表3。由于现实中电动汽车类型、服务耗时、道路曲折系数、道路畅通系数不唯一，为简化问题，本算例取平均值进行计算，其中各参数的取值如下:r0=0.1;rl=0.2;λ1=1.65万元/km;α=1.05 ～1.45;β=1.0 ～1.3;m=20;k =242次/辆;ω=1.1元/km;T =10 h/a;esoc=50% ～75%;LN=150 ～200 km。

表1 基础数据Tab.1 Basic data

表2 土地单价Tab.2 Land price 元/m2

表3 不同规模电池充电站的详细配置Tab.3 Detailed configurations of charging station with different scales

根据表1 的换电电池组需求，待建的充电站必须保证每天可以服务5 400 组电池，结合表2 和公式(17)，当电池充电站按规模1 配置时，最少需要6 座;当电池充电站按规模3 配置时，最多需要18 座电池充电站;以n(6 ～18)为循环变量，计算当前数量的电池充电站年总费用，取最小值对应的结果作为规模选择和布局的最优规划结果。

理论上，初始设备配置是造成不同规模电池充电站投资费用差异的主要因素，随着电池充电站的增多，其规模逐渐减小，单个电池更换系统占设备投资的比重升高。而电池更换系统对初始建设费用的影响最大，因此，电池充电站越多，总投资越高。对算例独立运行100次，计算出建设6 ～18 座电池充电站的最小费用分别为3 070.2，3 076.4，3 062.7，3 055.9，3 063.1，3 070.5，3 078.4，3 084.6，3 091.0，3 097.1，3 110.0，3 122.3，3 135.1万元。可见，在给定的条件下，规划区内建设9 座电池充电站时结果最优，优化后的各充电站位置和规模如表4，电池充电站的各项投资费用、用户路上耗电成本和时间如表5，其中，用户路上耗电时间是在假设电动汽车的行驶速度保持在100 km/h的基础上得出的。结果表明，该算法优化得到的结果既保证投资费用最少，又能够满足用户的便利性。图2 为采用CPSO 算法和PSO 算法的最优规划的动态演化过程，图3 为采用CPSO算法和PSO 算法的相邻两点的距离变化轨迹。从图2、3 可以看出:CPSO 算法在避免陷入早熟、收敛速度、最优结果等三方面均优于PSO 算法。结果表明，本文建立的电池充电站规模选择和布局模型一方面降低了建设成本，缩小了投资;另一方面又能满足不同交通密度的换电需求，符合预期设想。

表4 充电站位置的优化结果Tab.4 Optimization results of charging station location

表5 电池充电站优化的仿真结果Tab.5 Simulation results of charging station optimization

图2 CPSO 和PSO 算法的最优规划的动态演化过程Fig.2 Optimal planning of dynamic evolution process of CPSO and PSO

图3 CPSO 和PSO 算法的相邻两点的距离变化轨迹Fig.3 Change trajectory between two adjacent points in CPSO and PSO

4 结 论

(1)本文提出的数学模型中，既考虑了投资的费用，又加入了用户便利性，满足了建设方和使用方的需求，从全面性和经济性上都反映了充电站规划问题的实质。

(2)CPSO 算法利用混沌对初值的敏感性和混沌遍历性初始化种群;再通过逻辑自映射函数，形成混沌序列和优化变量取值范围的对应关系。通过混沌初始化可以使PSO 算法能从较好的初始值开始寻优，同时，迭代更新过程的停滞标准使搜索更为精细，克服了PSO 算法容易早熟、陷入局部极值的缺陷。

(3)对某小区电动汽车电池充电站进行了规划，证明了本文提出的优化计算模型是科学、可行的。

［1］徐敬，丁国安，颜鹏，等． 北京地区PM_(2.5)的成分特征及来源分析［J］．应用气象学报，2007，18(5):645-654．

［2］高赐威，张亮，薛飞，等．考虑集中型充电站定址分容的电网规划研究［J］．中国电机工程学报，2012，32(7):40-46．

［3］任玉珑，史乐峰，张谦，等．电动汽车充电站最优分布和规模研究［J］．电力系统自动化，2011，35(14):53-57．

［4］何永秀，周波，熊威．北京市电动汽车用户响应度研究［J］．电力建设，2013，34(1):1-6．

［5］Liu Z P，Wen F S，Ledwich G． Optimal planning of electric-vehicle charging stations in distribution systems［J］． IEEE Transactions on Power Delivery，2013，28(1):102-110．

［6］胡泽春，宋永华，徐智威，等． 电动汽车接入电网的影响与利用［J］．中国电机工程学报，2012，32(4):1-10．

［7］姚伟锋，赵俊华，文福拴，等． 基于双层优化的电动汽车充放电调度策略［J］．电力系统自动化，2012，36(11):30-37．

［8］He J，Zhou B，Feng C，et al． Electric vehicle charging station planning based on multiple-population hybrid genetic algorithm［C］// Control Engineering and Communication Technology 2012 International Conference． Liaoning University，Shenyang:IEEE，2012:403-406．

［9］纪震，廖惠连，吴青华． 粒子群算法及应用［M］． 北京:科学出版社，2009:28-45．

［10］刘长平，叶春明．基于逻辑自映射的变尺度混沌粒子群优化算法［J］．计算机应用研究，2011，28(8):25-27．

［11］张乐平，许燕灏，胡红，等． 电动汽车对电网影响的评价指标与评估方法［J］．电力建设，2013，34(8):46-51．

［12］李菱，李燕青，姚玉海，等．基于遗传算法的电动汽车充电站的布局规划［J］．华东电力，2011，39(6):1004-1006．

［13］刘自发，张伟，王泽黎．基于量子粒子群优化算法的城市电动汽车充电站优化布局［J］． 中国电机工程学报，2012，32(20):39-45．