基于改进粒子群优化算法的DG 准入容量与优化布置

胡美玉，胡志坚，史梦梦

(武汉大学电气工程学院，武汉市430072)

0 引 言

分布式电源(distributed generation，DG)是指发电功率不大，分散布置在配电网或用电负荷附近的小型发电单元，可高效、可靠地发电［1］。分布式发电技术主要包括微型燃汽轮机技术、燃料电池技术、光伏电池技术、风力发电技术。随着传统能源出现短缺、用户对电力质量要求不断提高以及绿色能源的开发和利用，分布式发电逐渐成为满足负荷增长需要、减少环境污染、提高能源综合利用效率、提高供电可靠性的一种有效途径，具有较好的应用前景。

DG 并入配电网后，电网节点电压、网络潮流、网损将发生变化且与DG 的接入位置与准入容量密切相关。近年来，国内外学者就配电网接纳DG 能力方面做了大量的研究。文献［2］给出了几种常见的DG优化配置模型和DG 优化配置方法。文献［3］建立了配电网馈线上DG 准入容量与接入位置的函数关系，并提出了3 种典型负荷分布下最优容量与最优位置的数学模型。文献［4］运用改进的最优布置算法分别求解放射状配电网连续解析模型和离散模型中DG最优接入位置。文献［5］运用简单梯度法研究DG 的最优位置与最优容量。文献［6］在研究DG 选址与定容问题时采用了新的进化方法。文献［7］采用遗传算法，研究DG 在配电网中的位置与容量均未知时的最优布置。文献［8］推导了辐射状配电网线损与DG准入容量、接入位置、功率因数的关系，分别研究单个及多个DG 接入对配电网线损的影响。

本文首先将单电源准入容量的数学模型推广应用至多电源，采用基于二次插值的粒子群优化(particle swarm optimization，PSO)算法，以网络有功损耗最小为目标函数，进行DG 布置的优化求解。

1 准入容量数学模型

准入容量为在不影响系统当前的安全、稳定性时，DG 允许注入的最大功率，最优容量可理解为在系统的经济性与安全性的最优的情况下接入的DG 的最大注入功率［9］。DG 准入容量与许多因素有关，已有很多学者研究了不同约束条件下DG 准入容量的计算。包括计及了电压调整和保护设置［10］、静态安全约束［11］、相间短路影响［12］、继电保护动作［13］、短路电流约束［14］等DG 准入容量的计算。本文中采用的是以节点电压和线路载流量为约束条件的准入容量计算模型［3］。

在负荷连续分布的馈线中，DG 接入点的电压为配电网中局部电压极大值［15］。根据基尔霍夫电流定律，忽略电压降落的横分量，可得到馈线中DG 接入点K 的电压。其中，实际配电网馈线中的负荷为离散分布，如图1 所示。

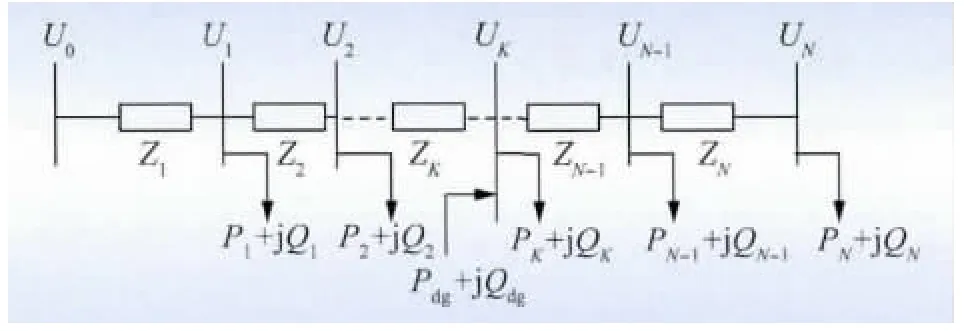
图1 离散负荷馈线模型Fig.1 Feeder model with discrete loads

DG 接入点电压可表示为

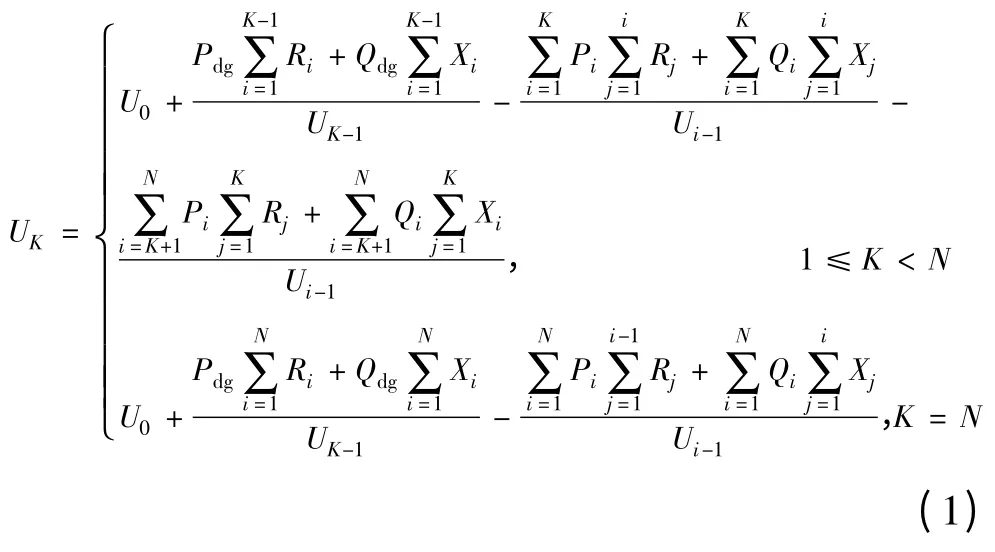
式中:Ri、Rj分别为节点i、j 支路电阻;Xi、Xj分别为节点i、j 支路电抗;N 为配电网任意馈线的节点数;Pi、Qi分别为节点i 的总有功、无功负荷;Pdg、Qdg分别为DG 的有功和无功容量［3］。

DG 采用具有恒定功率因数的PQ 节点模型，假设所有DG 的功率因数均为λ =0.98，根据Qdg与Pdg、λ 的关系，可得到DG 准入容量与接入位置的函数关系［3］。由于计算过程中忽略了线路损耗，导致DG 的容量偏小，因此引入修正因子α=1.05。

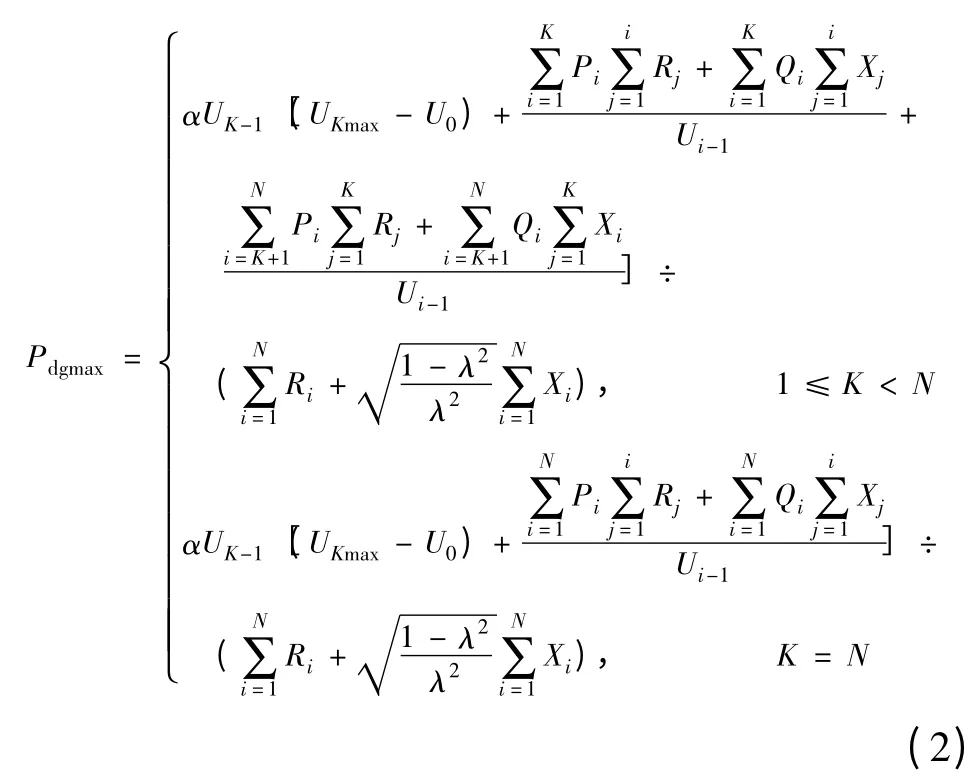
式中:UKmax为节点K 允许的最大电压;Pdgmax为DG在节点K 的最大准入容量。

由于公式(2)是根据离散分布的负荷馈线得到，实际配电网不可能只有1条馈线，节点必定存在分支线，在忽略线路损耗的情况下，结合DG 实际接入位置确定DG 所在馈线。分析在配电网中接入DG 的潮流分布可知，DG 的接入对DG 接入点到首节点之间的支路电流产生影响较大，而其他支路电流几乎不变。由此可确定多电源准入容量的数学模型如下:

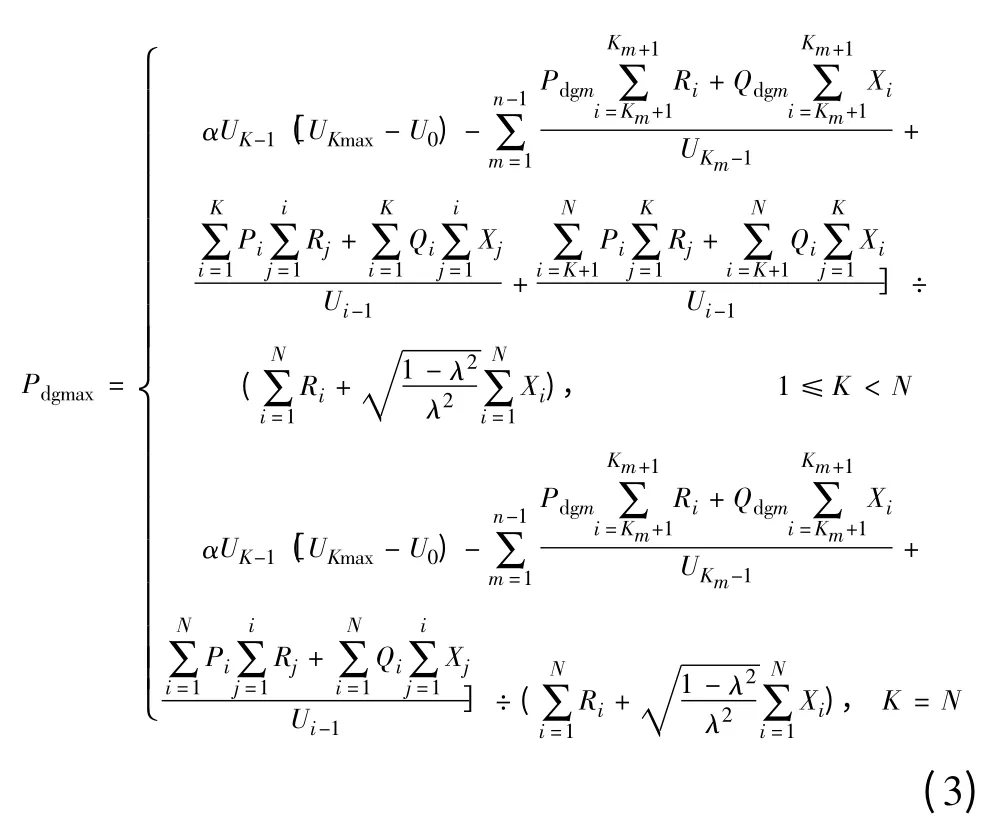
式中:n 为同一条馈线DG个数，Pdgm、Qdgm分别为该馈线中第m个DG 的有功和无功容量。

2 基于二次插值的PSO 算法

PSO 算法受鸟群觅食的行为规划与优化问题求解的启发而提出，也称为微粒群算法［16］。

每次迭代过程中，粒子的飞行速度和位置可根据个体的飞行经验和群体的飞行经验来进行动态调整，粒子速度与位置的更新方程为

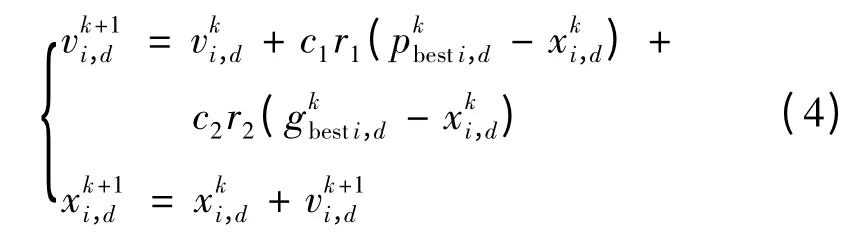
式中:vi，d为第i个粒子的d 维位置;k 为迭代次数;c1、c2称为加速因子;r1、r2为均匀分布在(0，1)区间上的随机数序列;pbest、gbest分别表示局部最优解和全局最优解;xi，d为第i个粒子的d 维位置。

PSO 算法在迭代初期全局搜索能力较好，但是在后期搜索能力较差，收敛速度慢，求解精度差，导致寻优能力降低，易陷入局部最优解。本文在PSO 算法中引进了如下的二次插值算子［17］。

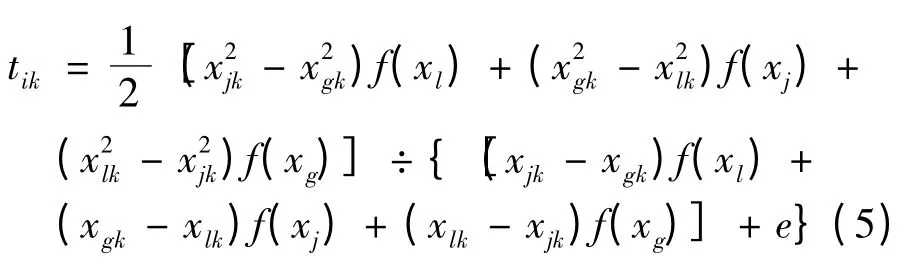
式中:f 为目标函数;e 是一个非常小正数，防止分母为0。xl、xj为m个粒子历史局部最优位置中的任意两个。xg为当前粒子位置。由该公式可得到xl，xj及xg的二次曲面的极小值点，具有较强的局部探索能力，可提高算法的收敛精度。

应用改进的PSO 算法，解决DG 在配电网中的最优布置步骤如下:

(1)初始化算法参数。算法参数包括最大迭代次数、种群大小、加速因子c1和c2、惯性权重因子w 、收缩因子h、最大速度和最大位置。

(2)初始化种群。在位置和速度限定范围内，任意给定粒子的位置和速度。

(3)调用潮流计算程序得到网络损耗，计算粒子的适应度函数值，确定初始的个体最优极值pbest和全局最优极值gbest。

(4)运用计算得到的pbest和gbest，更新粒子的位置与速度。

(5)进行潮流计算，得到种群中每个粒子的适应函数值，确定个体历史最优极值pbest和全局最优极值gbest。

(6)采用二次插值PSO 算法寻找二次插值，评价二次插值的适应函数值，与gbest进行比较，若x 值优于gbest，则gbest=x;否则gbest不变。

(7)检查是否达到最大迭代次数，若没有，则转第(4)步，否则转第(8)步。

(8)绘制网络损耗变化曲线，输出最优解。

3 DG 优化布置模型

3.1 目标函数

本文以配电网有功损耗fp．loss最小为目标函数研究DG 选址，即

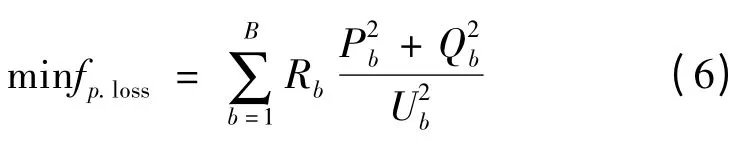
式中:B 为电网总支路数;Rb为第b条支路的支路电阻;Ub、Pb、Qb分别为支路b 末端节点电压、有功功率、无功功率。

3.2 约束条件

(1)节点电压约束:

式中:N 为节点总数;Vmin、Vmax分别表示各节点电压允许的最小值和最大值。

(2)支路电流约束:

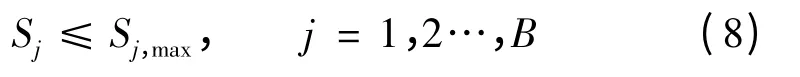
(3)网络潮流约束:

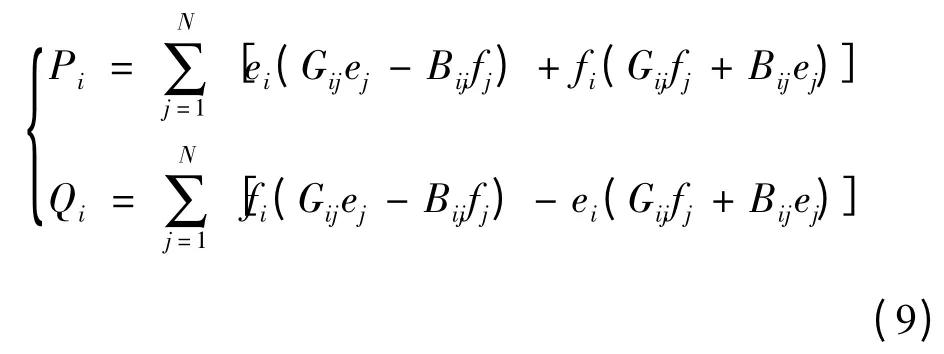
式中:ei、fi分别表示节点i 电压Vi的实部和虚部;Gij、Bij表示节点i、j 互导纳的实部与虚部;Pi、Qi分别为节点i 注入的有功功率、无功功率。

4 算例分析

4.1 算例描述与算法参数设置

本文采用IEEE 33 节点配电系统［18］为算例，如图2 所示。该系统的额定电压为10.5 kV，总负荷为5 084.26 +j2 547.32 kVA，共有33个节点，37条支路，其中有5条支路为联络开关，分别为支路33、34、35、36、37。

改进的粒子群算法初始参数设置如下:种群规模200;最大迭代次数100;学习因子c1、c2均取2.05;惯性权重ω 的最大值取1.2，最小值取0.4。

4.2 单电源最优布置

将节点1 看作为平衡节点，DG 看作为具有恒功率因数的PQ 节点。分别应用PSO 算法和改进的PSO 算法对单电源进行最优布置。优化结果如图3 所示。

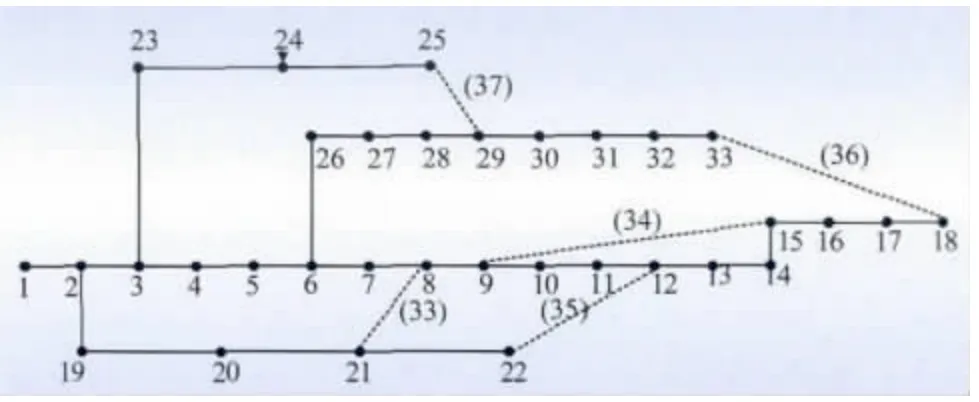
图2 IEEE 33 节点系统结构Fig.2 Structure of IEEE 33-node system

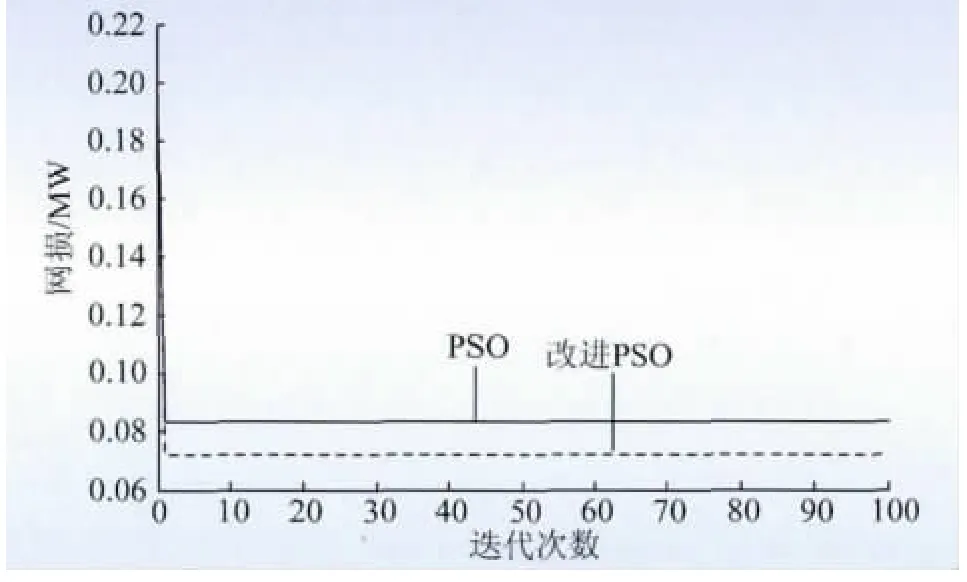
图3 单电源优化结果Fig.3 Optimization results of signal power source

计算结果表明，采用PSO 算法在配电网中接入单电源时，最优网损为0.083 404 MW，减小为原来的35.59%(原始网损大小为0.203 MW)，此时粒子位置为节点26，最优容量为2.658 3 MW。采用改进PSO 算法进行优化计算，粒子全局最优位置还是节点26，最优容量为2.660 2 MW，此时最优网损大小为0.075 184 MW，减小为原来的35.56%。由此可见，改进的优化算法提高了收敛性能。

4.3 多电源最优布置

本文以配电网中接入2个电源为例分析多电源准入时的网损情况。设定粒子维度值为2，网损变化如图4 所示。

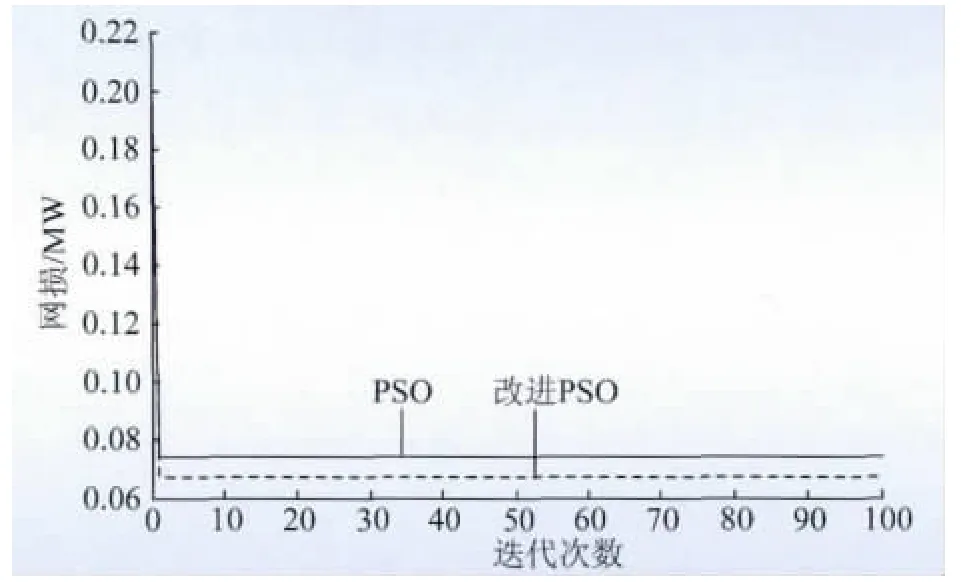
图4 多电源优化结果Fig.4 Optimization results of multiple power sources

采用PSO 和改进PSO 这2 种优化算法研究多电源最优布置，进一步证实改进算法的实用性。

仍将节点1 看作为平衡节点，DG 看作为具有恒功率因数的PQ 节点。表1 为分别采用上述2 种优化算法的计算结果。

表1 改进PSO 算法和PSO 算法结果对比Table 1 Comparison of PSO and improved PSO algorithms

由优化结果可知，DG 的接入位置均靠近负荷端，由此可说明负荷端接入DG 对网络潮流、网络损耗有更好的改善效果。

5 最优布置潮流分析

5.1 单电源布置潮流分析

由上节可知，网损最优时，DG 的接入位置均靠近配电网馈线末端。在Simulink 中建立IEEE-33 节点配电网模型，根据优化程序的计算结果，分别在节点8 ～33 接入最优容量。DG 采用发电机模型，设为PQ 节点，配电网网络损耗与DG 的接入位置的关系如图5 所示。

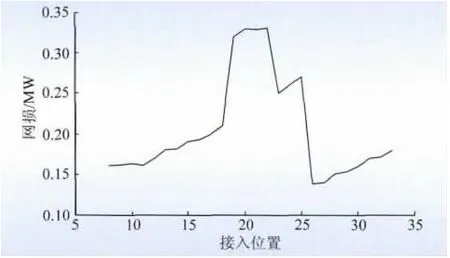
图5 配电网网损分布Fig.5 Power loss distribution in distribution network

并网前，配电网的网络损耗为0.33 MW，并网后最优网络损耗为0.14 MW，为并网前的42.42%。此时，DG 的接入位置为节点26，与程序得到的最优网络损耗对应的粒子位置相同。

5.2 多电源最优布置潮流分析

图6 为根据稳态潮流绘制的多电源并网前后系统节点电压分布。在IEEE 33节点系统中节点18、33分别接入容量为0.586 4，1.725 6 MW 的DG 时，有功网损大小为0.11 MW，减小为原来的33.33%，与算法的计算结果一致，验证了算法优化结果的正确性。

比较图6 中的节点电压分布曲线可知，在IEEE 33节点系统接入2个DG 后，节点电压均有所上升，且在DG 接入点附近，节点电压上升较为明显。节点电压分布曲线趋于平缓，维持在馈线额定电压附近。由此可见DG 接入配电网时，对配电网的节点电压有支撑作用，并且DG 的接入点离母线首节点越远，对配电网的电压支撑效果越明显。

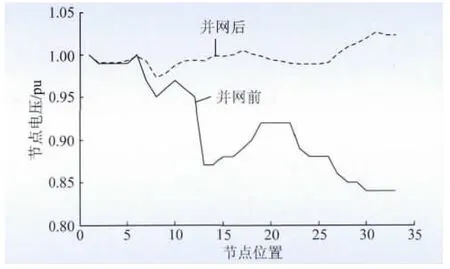
图6 配电网节点电压分布Fig.6 Node voltage distribution in distribution network

6 结 论

本文以网络损耗最小为目标函数，以节点电压、支路容量、网络潮流方程为约束条件，研究了DG 在配电网中的准入容量和优化布置。

将馈线中单个DG 准入容量的数学模型推广应用至含分支线路的配电网中，并由此推导多电源准入容量与接入位置的函数关系;分别采用改进PSO 算法和PSO 算法，结合实际算例，计算得到最优网损时单电源及多电源的接入位置和最优容量;改进PSO算法的仿真结果优于PSO 算法的结果，这表明改进PSO 算法提高了收敛精度;分析单电源优化结果下的最优网损分布和多电源优化结果下的节点电压分布，验证了算法优化结果的正确性。算例结果表明，DG 可有效改善配电网网损，提高配电网的供电电压质量。

［1］梁有伟，胡志坚，陈允平．分布式发电及其在电力系统中的应用研究综述［J］．电网技术，2013，27(12):71-75．

［2］王守相，王慧，蔡声霞．分布式发电优化配置研究综述［J］．电力系统自动化，2009，33(18):110-115．

［3］文升，顾洁，程浩忠，等．分布式电源的准入容量与优化布置的实用方法［J］．电力自动化设备，2012，32(10):109-114．

［4］顾承红，艾芊，程浩忠，等．配电网中分布式电源最优布置［J］． 上海交通大学学报，2007，41(11):1896-1900．

［5］Rau N S，Yih-heui M． Optimum location of resource in distributed planning［J］． IEEE Transcation on Power System，1994，9(4):2014-2020．

［6］Kim J O，Park S K，Park K W，et al． Dispersed generation planning using improved Hreford ranch algorithm［J］． Electric Power System Research，1998:678-683．

［7］Celli G，Pilo F． Optimal distributed generation allocation in MV distribution networks［C］ //Proceedings of 22ndIEEE Power Engineering Society International Conference on Power Industry Computer Applications．Sydney，Australia:IEEE，2001:81-86．

［8］张瑜，孟晓丽，方恒福，等．分布式电源接入对配电网线损的影响分析［J］．电力建设，2011，32(5):67-71．

［9］Lundberg S，Thiringer T，Petru T．Electrical limiting factors for wind energy installations in weak grids［J］． International Journal of Renewable Energy Engineering，2001，3(2):305-310．

［10］胡骅，吴汕，夏翔，等．考虑电压调整约束的多个分布式电源准入功率计算［J］．中国电机工程学报，2006，26(19):13-17．

［11］Cai J，Ma X，Li L．Chaotic particle swarm optimization for economic dispatch considering the generator constraints ［J］． Energy Conversion Manage，2007，48(2):645-653．

［12］雷金勇，黄伟，夏翔，等．考虑相间短路影响的分布式电源准入容量计算［J］．电力系统自动化，2008，32(3):82-86．

［13］王江海，邰能灵，宋凯，等．考虑继电保护动作的分布式电源在配电网中的准入容量研究［J］． 中国电机工程学报，2010，30(22):37-43．

［14］连欣乐，吴政球，赵柯宇，等．计及短路电流约束的分布式电源准入容量的计算［J］．电力科学与技术学报，2008，23(1):51-55．

［15］王志群，朱守真，周双喜，等．分布式电源接入位置和注入容量限制的研究［J］．电力系统及其自动化学报，2005，17 (1):53-57．

［16］Kennedy J，Eberhart R． Particle swarm optimization ［C］//Proceedings of IEEE International Conference on Neural Networks，Piscataway:IEEE Service Center，1995:1942-1948．

［17］钱伟懿，卢静．二次插值的粒子群优化算法［J］．计算机工程与应用，2013，49(4):35-38．

［18］刘健，毕鹏翔，董海鹏．复杂配电网简化分析与优化［M］． 北京:中国电力出版社，2002:276-277．