工程设计方法在串级调速系统中的应用
2014-02-13詹庄春
詹庄春
(华南农业大学珠江学院信息工程系,广东广州510900)
工程设计方法在串级调速系统中的应用
詹庄春
(华南农业大学珠江学院信息工程系,广东广州510900)
将工程设计方法应用在异步电动机串级调速系统中,目的是为系统参数调整寻找一种捷径,以弥补单纯经验调节法的不足,意义是争取设计高效的一次尝试.采用例证的方式,构建了系统的Matlab仿真模型,并对其测试,通过波形效果图的比较得出结论:应用工程设计方法的串级调速系统达到了良好的静动态性能.
工程设计方法;串级调速;调节器;Matlab
对调节器参数的整定,过去用的较多的是经典动态校正方法,它需要设计者具有扎实的理论基础、丰富的实际经验和熟练的设计技巧,初学者不易掌握这些.目前,关于串级调速方面的研究,较多的是探索硬件的新结构和控制的新方法,其均有效果体现,但是,或使系统结构变得复杂了[1],或对控制理论要求较高[2];其次,更有大量的单纯经验调节法,体现出设计工作繁琐低效.而工程设计方法的介入,可以很好的解决以上问题.
1 工程设计方法简介
工程设计方法突出主要矛盾.它通过对传递函数作近似处理,再配以适当的调节器,就可将控制对象化为典型Ⅰ型系统或Ⅱ型系统[3],其传递函数为:

首先,对于典型Ⅰ型系统,根据系统动态跟随性能指标,其参数设置可查表1.

表1 典型Ⅰ型系统动态跟随性能指标与参数的关系

2典型I型系统动态抗扰性能指标与参数的关系
当有阶跃干扰信号作用时,针对在典型Ⅰ型系统环境下的调速系统,分析扰动作用点如图1所示的一种情况,取KT=0.5,根据系统抗扰性能指标,其参数设置可查表2.

图1 典型I型系统在一种扰动作用下的动态结构图
其次,对于典型Ⅱ型系统,令h=τ/T,根据系统动态跟随性能指标,其参数可查表3.
当有阶跃干扰信号作用时,针对在典型Ⅱ型系统环境下的调速系统,分析扰动作用点如图2所示的一种情况,根据系统动态抗扰性能指标,其参数设置可查表4.

图2 典型Ⅱ型系统在扰动作用下的动态结构图

表4典型Ⅱ型系统动态抗扰性能指标与参数的关系
最后,由表1可知,一般取:KT=0.5,ζ=0.707;由表2可知,控制对象的两个时间常数比值越大,则动态降落越小,但恢复时间较长;由表3可知,在h=5时达到最短;由表4可知,一般取h=5.在跟随性能方面,经表1与表3对比可知,典型Ⅰ型系统的超调量较小;在抗扰性能方面,经表2与表4对比可知,典型Ⅱ型系统的恢复时间较短.
2 异步电动机双闭环控制的串级调速系统结构原理
串级调速系统主要由转速调节器、电流调节器、“交—直—交”电力电子装置以及电动机等组成,通过电流互感器、测速机,形成电流负反馈和速度负反馈的双闭环结构,如图3所示为系统框图[4].

图3 串级调速系统框图
图中异步电动机以某种转差速运行,其转子电动势经不控整流器输出直流电压,此电压与晶闸管有源逆变电压一起构成了转子直流回路.于是,通过控制晶闸管逆变角,来改变转子直流回路中的电流,就可以实现对电机转速的调节.
在转子直流回路中,设空载转速为n0,负载转速为n,转子静止时开路电压为Ud0,逆变器输出的空载电压为Ui0,转子直流回路总电感、总电阻及电流分别为L∑、R∑、id,可得转子直流回路的传递函数.
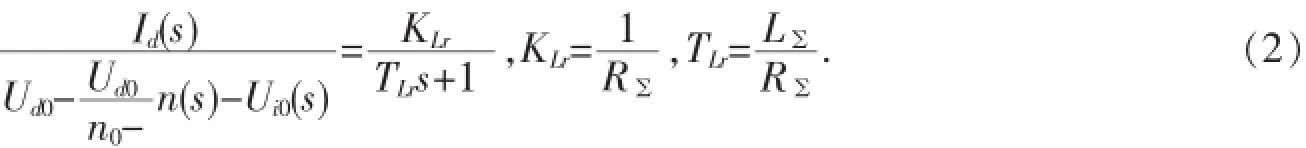
对于异步电动机,设同步角转速为Ωct,在s=1时折算到转子侧每相漏抗为XD0,考虑换相重叠对整流电路的影响,负载电流为IL,飞轮惯量为GD2,忽略线路损耗,可得异步电动机的传递函数.

对晶闸管逆变器,设触发电路的控制电压为Uct,放大系数为Ks,失控时间为Ts.另外,设电流互感器反馈系数为IL,测速机反馈系数为fn,速度给定电压为Un*,转速调节器为ASR,电流调节器为ACR,则可将系统框图转化成系统动态结构图,见图4.

图4 串级调速系统动态结构图
3 工程设计方法在串级调速系统中的应用举例
设双闭环控制的串级调速系统,采用三相桥式整流装置和逆变器调速,电源频率50 Hz.异步电动机的基本数据为:Pnom=120 KW,Unom=380 V,nnom=1 370 r/min,E20=60 V,I2nom=125.2 A,XD0=0.94 Ω,GD2=3.85 N·m2.转子直流回路:L∑=88.3 mH,R∑=1.214 Ω.逆变器Ts=0.001 7 s.试对系统进行动态参数设计.
第一步,被控装置的参数计算.设最小逆变角βmin=30°,根据式(2)(3),可知,

第二步,电流调节器设计.为抑制电流波动造成的高频干扰,需增加电流低通滤波,又为了平衡滤波环节带来的延滞,同时需增加给定滤波环节,两者时间常数均为Toi(取2 ms).不考虑负载扰动,忽略转差电压扰动对电流环的影响.整个电流调节系统的动态结构图如图5(a)所示,通过简化得到图5(b).电流环近似处理的条件为TsTois2<<1.
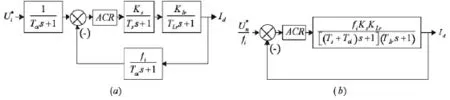
图5 电流环的动态结构图及其简化处理
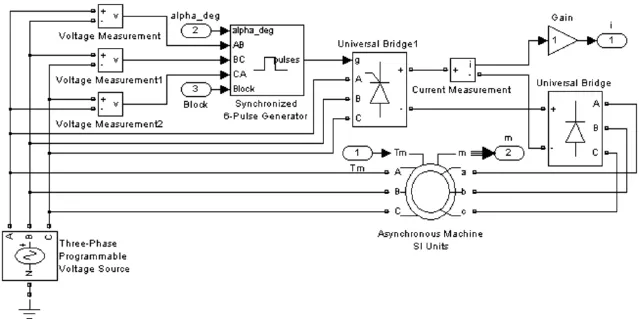
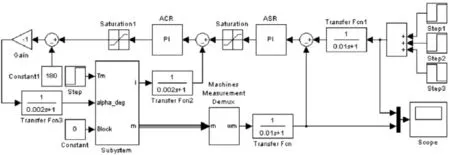
电流环的调节对象由一个小惯性环节和一个大惯性环节组成,由于TLr 第三步,转速调节器设计.令T∑i=Ts+Toi,电流闭环传递函数可降阶及其近似处理条件为.经电流闭环等效后,转速环的调节对象由一个小惯性环节和一个积分环节组成.为抑制转速纹波造成的高频干扰,需增加转速低通滤波,又为了平衡滤波环节带来的延滞,同时需增加给定滤波环节,两者时间常数均为Ton(取10 ms).整个转速调节系统的动态结构图如图6(a)所示,不考虑负载扰动时,通过简化得到图6(b),简化条件为2T∑iTons2<<1. 图6 转速环的动态结构图及其简化处理 为增强抗扰性能,转速环按典型Ⅱ型系统设计,故ASR也选择PI调节器.令转速开环增益为KN,fn=1,得(6)式.校验转速环近似处理条件,均满足. 在Matlab的Simulink环境下,建立串级调速系统模型.主电路由三相对称交流电压源、二极管转子整流器、晶闸管逆变器、绕线式交流异步电动机、脉冲信号分配器以及电流表、传输器等部分组成[5],如图7所示. 图7 串级调速系统主电路模型 各模块参数均按举例数据进行设置(电机其他参数:R1=1.083 Ω,R2=1.083 Ω,X1σ=5.974 mH,X2σ=5.974 mH,Xm=0.203 7 H,J=0.01 kg·m2,F=0.005 752 N·m·s,P=2). 然后将主电路建立为一个子系统,按照串级调速系统动态结构图,构建系统的双闭环控制电路模型.该模型包括主电路子系统、给定环节、电流调节器、速度调节器、电机多功能检测仪、限幅器、滤波器以及反相器、示波器等[6],如图8所示. 图8 双闭环控制的串级调速系统仿真图 参数设置:Step=0,Step1=90,Step2=40,Step3=-10,Saturation=[0 180],Saturation1=[30 90].根据经验调节控制器参数,获得输出波形如图9所示.据工程设计方法调节控制器参数(Ki=1.6,τi=72.73 ms,Kn=15.674,Tn=0.087s),获得输出波形如图10所示.比较两者可知,运用工程设计方法的调速系统达到了良好的静动态性能,且在此基础上,还能作进一步微调,使系统性能更佳. 图9 经验调试方法的串级调速效果图 图10 工程设计方法的串级调速效果图 采用将实践经验与理论计算有机融合在一起的工程设计方法,当基于控制对象的精确模型时,既可使系统达到快准稳的效果,又可免除繁琐的调试过程.它来源于实践,又高于实践,将之应用于串级调速系统控制器的一次尝试是成功的,在控制器的硬件和软件方面,该方法均可应用. [1]刘中良,陈伟华,於江赟.内馈斩波串级调速系统中斩波器主电路的分析和仿真[J].电机与控制应用,2012,39(3):25-28. [2]陈冲,胡国文.基于神经网络控制的直流调速系统仿真与分析[J].计算机仿真,2013,30,(04):356-360. [3]陈伯时.电力拖动自动控制系统[M].第2版.北京:机械工业出版社,2000. [4]孙炳达.自动控制原理[M].第3版.北京:机械工业出版社,2011. [5]田莉.绕线式异步电动机双闭环串级调速系统的仿真[J].黑龙江科技信息,2012,(33):103. [6]贾建强,韩如成,左龙.基于MATLAB的交流电机调速系统建模与仿真[J].电机与控制学报,2000,4(2):91-93. The application of engineering method in cascade speed regulation system ZHAN Zhuang-chun Engineering method is used in asynchronous motor cascade speed regulation systems,The purpose is to find a shortcut for system parameter adjustment,and make up for the inadequacy of pure experience regulating method.Its significance is an attempt to obtain design efficiency.By the way of example,the Matlab simulation model of the system is built.Then,through the test,the comparison of the waveform rendering concluded that engineering method of cascade speed regulation system has reached the good static and dynamic performance. engineering method;cascade speed regulation;regulator;Matlab TP214+.5 :A :1007-5348(2014)10-0043-05 (责任编辑:李婉) 2014-07-06 詹庄春(1978-),男,江西鄱阳人,华南农业大学珠江学院信息工程系讲师,硕士,主要从事电气自动化方面的研究.


4 串级调速系统的仿真测试及其调节效果的比较
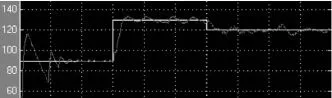
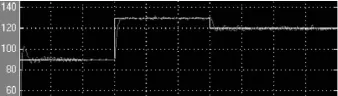
5 结语
(Zhujiang Institute of South China Agricultural University,Guangzhou 510900,Guangdong,China)
