不同地形条件下多种GPS高程拟合模型的适应性研究
2014-02-13董书晓
董书晓 甘 淑
(昆明理工大学国土资源工程学院,昆明 650093)
GPS 高程是以WGS-84 椭球面为基准面的大地高H,而我国的测量高程系统采用的是以(似)大地水准面为基准面的正常高Hr,两者间的差距即为高程异常ζ[1]:

由于WGS-84 椭球面与(似)大地水准面之间数学关系复杂,致使高程异常值既不是常数,也难以用合适的函数式完全无误地表达,导致GPS 高程在实际应用中受到限制,特别是在地形复杂的山区。
GPS 高程转换方法有二次曲面拟合法、多面函数拟合法、Shepard 拟合法、BP 神经网络法、支持向量机等。不同的拟合方法有不同的特点,适应性也不一样,使得同一种模型在不同地形条件下的拟合效果也不完全相同。本文通过对常用的二次曲面模型、多面函数模型、Shepard 模型进行分析,并根据各自的优势和局限性建立组合模型,通过对几种模型的拟合精度进行对比,评价其对不同地形的适应性。
1 GPS 高程异常拟合的数学模型
1.1 二次曲面拟合法
设GPS 控制点有n 个,控制点坐标xi、yi与高程异常值ζi(i=1,2,…,n)之间存在以下关系[2]:
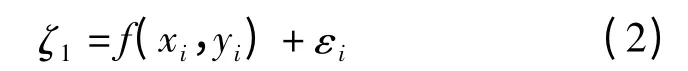
式中,f(x,y)为ζ 的拟合值,εi为拟合误差。当采用二次函数为拟合函数时:

式中,ai(i=1,2,…,5)为待定系数。于是有:

式中,

根据每个已知点的x、y 及ξ 值,可组成式(4),在最小二乘法条件下,求解出唯一的一组参数A,进而对同一范围内的待求点进行高程异常拟合。
1.2 多面函数拟合法
多面函数拟合法的核心思想是:任何数学表面和不规则圆滑表面,总可用一系列规则的数学表面的总和以任意精度逼近。其一般形式为[3]:

式中,aj是待定系数,Q(x,y,xj,yj)是多面函数的核函数。核函数有多种类型,为便于计算,一般采用具有对称性的距离型,即
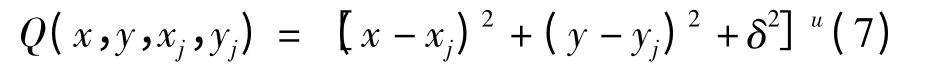
式中,δ 为平滑因子,μ 一般取1/2 或-1/2。当μ=1/2 时,核函数称为正双曲面函数;当μ=-1/2 时,核函数为倒双曲面函数。
若有m 个已知GPS 水准点数据,将这m 个数据点中的n 个作为核函数的中心点。令Qij=Q(xi,yi,xj,yj),则各数据点应满足:

式中,i 为中心点个数,i=1,2,…,n,j 为GPS 水准点个数,j=1,2,…,m。由此可列出误差方程:

根据最小二乘法可得:

将其代入式(8),即可得到测区内任一点的高程异常拟合值[4]。
1.3 Shepard 曲面拟合法
对于大量的离散数据,Shepard 提出局部逼近模型[5-7]。设有m 个已知点,坐标为(xi,yi),fi为已知点(xi,yi)处的高程异常值,Shepard 曲面可写为如下形式:

式中,μ 为一大于1 的常数,ri表示各点间的距离,ri为各点关于距离的权函数。在其模型结构中,将对拟合点高程异常值有重要影响的范围设定为一个以拟合点为圆心、半径为R 的圆,在拟合区内分为两个环带[8],则权函数ρ(r)可定义为:
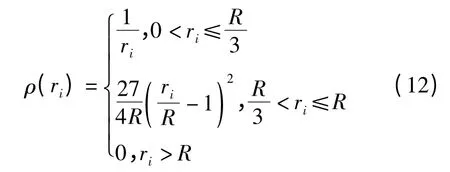
搜索半径R 的选取应根据已知点密度及实际地形情况灵活调整。
2 基于“移去-恢复法”的组合模型
2.1 “移去-恢复法”原理
根据物理大地测量学,高程异常值可表示为[9]:

式中,ξGM为通过地球重力场模型计算出的长波分量;ξΔg为用斯托克斯积分公式得到的中波分量;ξT为地形起伏的影响,表示大地水准面短波分量。在小区域GPS 网中,高程异常值的中长波分量基本不变,引起其变化的主要是地形起伏引起的短波分量。这一现象在地形起伏较大的高原山区尤为明显。
“移去-恢复法”的原理实质上是先拟合出高程异常值中长波分量部分并将其移去,再对其短波分量进行拟合,然后将待定点上的长波分量进行恢复,得到最终的拟合结果。
2.2 两种组合模型的选择
根据实验,二次曲面模型能对中长波项进行较好拟合,而对短波项拟合效果不佳;多面函数模型虽对整体拟合效果不好,但对局部变化反应敏感;Shepard 曲面拟合法只能对噪声趋势性信号拟合较好,而无法对整体变化平缓的中长波项进行很好的拟合[10]。
根据以上分析,构建两种不同的组合模型。
1)在测区内选取m 个GPS 水准点作为二次曲面函数的已知点,并选择n 个作为检测点(待求点)进行拟合,求出各已知点的高程异常拟合值ξ0和待求点的拟合值ξ拟。
2)求出m 个GPS 水准点上的拟合残差:

3)将各点的残差值ε0作为已知量,利用多面函数模型,求出各待求点残差的拟合值,组成第一种组合模型,即“二次曲面+多面函数组合模型”。拟合的待求点高程异常值为:

4)将各点的残差值ε0作为已知量,利用Shepard 模型求出各待求点残差的拟合值ε2拟,组成第二种组合模型,即“二次曲面+ Shepard 曲面模型”。拟合的待求点高程异常值为:

3 实例分析
3.1 实例选取及数据处理方法
设计两个具有代表性的工程实例,模拟基于平原地形和山区地形条件下最佳高程异常拟合模型的选取。
实例1:某市D级GPS 网,面积约为250 km2,区域内地势平坦,高程异常值变化很小,属于平原地形。测区共布设40 个观测点,并进行三等水准联测。选用均匀分布于整个测区的10 个点作为已知点,其余30 个点作为检测点(待求点),用来检验各种方法的拟合效果,如图1。
实例2:云南某地区C级GPS 网共布设24 个GPS 水准点,并进行三等水准测量。测区总面积约2 000 km2,地形起伏较大,高程异常值变化很大,属于典型的高原山区地形。选择均匀分布在测区内的16 个点作为已知点,其余8 个点作为检测点(待求点),用来检验各种方法的拟合效果,如图2。
对上述两组数据分别采用5 种模型进行计算,并采用待求点的外符合精度m 对拟合方法进行评价:
式中,v 为检测点的已知高程异常其拟合值之差,n为待求点个数。

图1 平坦地区控制点位分布图Fig.1 Distribution of control points in flat area

图2 山区地形控制点位分布图Fig.2 Distribution of control points in mountainous area

表1 平坦地区5 种拟合方法计算结果(单位:cm)Tab.1 The results calculated with five fitting methods in flat area(unit:cm)
3.2 平坦地形区域案例分析
表1 为平坦地形条件下5 种高程异常拟合方法得到的结果,图3 为5 种模型的高程异常拟合残差值曲线。可以看出,在该测区内,就单一拟合模型来说,无论是拟合残差分布的均匀性还是检测点的中误差,二次曲面法拟合精度最高,多面函数次之,Shepard 拟合法在R=10 km 时精度达到最好,但远低于前二者。而对于组合模型,两种组合模型的拟合精度都略高于任何一种单一模型,但优势都不十分明显。这是因为,两种组合模型都充分利用了二次曲面模型善于拟合高程异常中长波分量以及多面函数与Shepard 拟合法善于拟合高程异常中短波分量的特点,所以拟合效果稍好于单一模型。但因为平原地区地形起伏变化较小,高程异常中短波分量变化量也较小,因此运用组合模型的优势不是很明显。
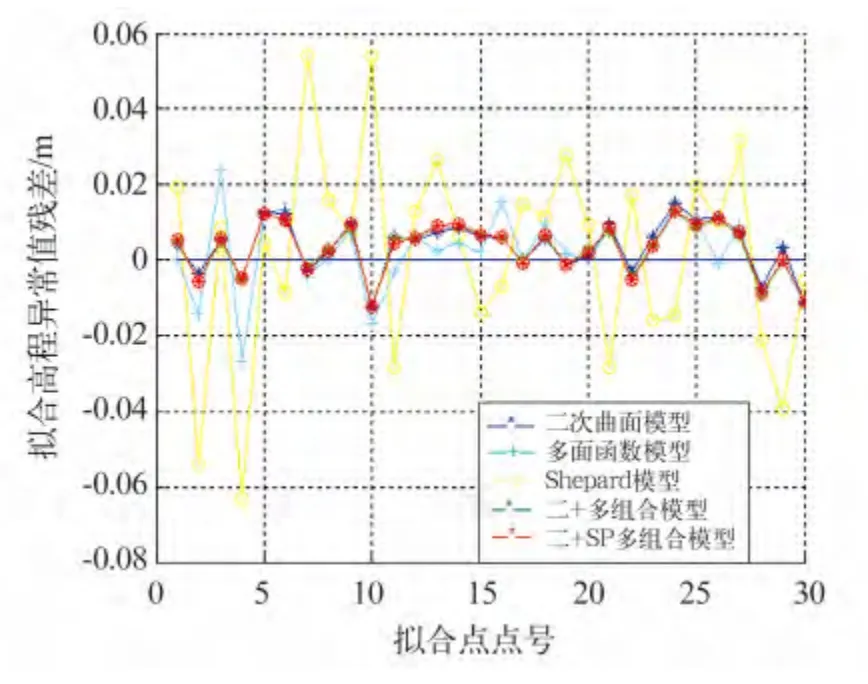
图3 5 种模型对平坦地区拟合残差图Fig.3 Fitting residual plot with five models in flat area
3.3 复杂山地地形区域案例分析
表2 为山区地形条件下5 种拟合模型得到的统计结果,图4 为5 种高程异常拟合模型的高程异常拟合残差值曲线。可以看出,就单一模型而言,3 种拟合模型的拟合精度都不是很好。其中,二次曲面拟合精度最差,多面函数次之,而Shepard 拟合法在R=30 km 时达到最好。和二次曲面模型及多面函数模型相比,Shepard 拟合法精度略好于二者。对于组合模型来说,两种组合模型的拟合精度都要好于各自的单一模型,而且二次曲面+Shepard 组合法比二次曲面+多面函数组合法效果要好。这说明,在高程异常短波分量变化较大的山区,各种单一模型的局限性反映得愈加明显。具体而言,对高程异常长波分量有较好拟合效果的二次曲面模型由于不能较好地反映短波分量的变化趋势,所以拟合效果最差;对短波分量有明显反映的多面函数和Shepard 拟合法有较好的拟合效果,但二者都无法较好地顾及高程异常的长波分量和短波分量,所以没有组合模型的拟合效果好。

表2 山区地形中5 种拟合方法计算结果(单位:cm)Tab.2 The results calculated with five fitting methods in mountainous area(unit:cm)

图4 5 种模型对山区地形拟合残差图Fig.4 Fitting residual plot with five kinds of models in mountainous area
4 结 论
1)二次曲面模型在平坦地区即便已知点较少也能达到很好的拟合精度,而多面函数模型及Shepard 模型虽然在平坦地区拟合精度不佳,但在山区地形中有较好的拟合效果。
2)在Shepard 模型中,其影响范围R 不是一成不变的,在实际中应根据测区地形和已知点密度而定。在平坦地区影响范围稍小,而在山区地形中影响范围要大。
3)两种组合模型在两种地形条件下都有较好的拟合效果,在山区地形中优势更明显,二次曲面+Shepard 组合模型尤其适应起伏变化的山区地形。
4)5 种拟合模型中,没有一种能适用于所有地形条件,在应用中应根据具体环境加以选择。
1 陶本藻.GPS 水准似大地水准面拟合和正常高计算[J].测绘通报,1992(4):14-18.(Tao Benzao.GPS leveling fitting geoid and calculation of normal high[J].Bulletin of Surveying and Mapping,1992(4):14-18)
2 乔仰文,辛久志,王晓辉.GPS 高程拟合的几种常用方法[J].东北测绘,1999,22(2):10-11.(Qiao Yangwen,Xin Jiuzhi,Wang Xiaohui.Several common methods of GPS height fitting[J].Northeast China Surveying and Mapping,1999,22(2):10-11)
3 金时华.多面函数拟合法转换GPS 高程[J].测绘与空间地理信息,2005,28(6):44-47.(Jin Shihua.The polyhedral function fitting method converting GPS height[J].Surveying and Mapping and Spatial Geographic Information,2005,28(6):44-47)
4 陈克杰,黄观文,刘站科.基于多面函数与Shepard 插值的高程异常综合拟合法[J].工程勘察,2010(5):50-52.(Chen Kejie,Huang Guanwen,Liu Zhanke.Based on the abnormal height of polyhedral function and shepard interpolation fitting method[J].Engineering Investigation,2010(5):50-52)
5 Franke R.Scattered data interpolation tests of some methods[J].Mathematics of Computation.,1982,38(157):181-200.
6 Franke R,Nielson G.Smooth interpolations of large sets of scattered data[J].International Journal for Numerical Mathods in Engineering,1980,15:1 691-1 704.
7 徐遵义.改进的Shepard 算法及其在重力异常插值中的应用[J].武汉大学学报:信息科学版,2010,35(4):477-480.(Xu Zunyi.Improved shepard algorithm and its application in gravity anomaly interpolation[J].Geomatics and Information Science of Wuhan University,2010,35(4):477-480)
8 欧阳欣,张立亭.GPS 水准拟合模型的比较与分析[J].测绘工程,2009,18(2):32-33.(Ouyang Xin,Zhang Liting.The comparison and analysis of GPS leveling fitting model[J].Surveying and Mapping Engineering,2009,18(2):32-33)
9 赵建虎,刘经南,张红梅.顾及格网数据考虑地形改正的GPS 水准高程拟合[J].武汉测绘科技大学学报,1999,24(4):346-347.(Zhao Jianhu,Liu Jingnan,Zhang Hongmei.To consider the terrain grid data correction of GPS leveling height fitting[J].Journal of Wuhan Technical University of Surveying and Mapping,1999,24(4):346-347)
10 侯本军,钟波,王文庆.基于二次曲面的Shepard 拟合法在GPS 水准中的应用[J].测绘工程,2007,16(1):36-38.(Hou Benjun,Zhong Bo,Wang Wenqing.Shepard based on quadric surface fitting method in the application of GPS leveling[J].Surveying and Mapping Engineering,2007,16(1):36-38)
