高等数学复习题变式多解的研究

邱云兰

(韶关学院韶州师范分院数学系,广东韶关512009)

高等数学复习题变式多解的研究

邱云兰

(韶关学院韶州师范分院数学系,广东韶关512009)

课本习题的改造是"数学探究"的重要渠道.高等数学课堂教学的核心任务主要是培养学生的思维探索能力,数学思维探索能力的提高在于选题、变式、解题质量的提高,而非选题、变式、解题的数量的增多.选题要把握"三原则"、变式要多角度.这样,不但可起到沟通各知识的纵横联系,而且能促进解题策略的逐步优化,培养学生的思维能力、分析问题和解决问题的能力.

高数教学;习题变式;解题方法;探索能力

复习题是数学教科书的一个重要组成部分,有着巩固和深化知识,补充与延伸知识,综合运用知识,领悟数学思想与方法等功能[1-2].变式是对某种范式的变化形式,不断变更有关情境或改变思维的角度,在保持事物的本质特征不变的情况下,使事物的非本质属性不断迁移的变化方式.变式既是一种重要的思想方法,又是一种行之有效的教学方式[3].波利亚说:"一个专心认真备课的教师能够拿出一个有意义的但又不重复的题目,去帮助学生挖掘问题的各个方面,使得通过一道题,就好像通过一道门户,把学生引入一个完整的理论领域.解题的过程,就是不断变更题目的过程".由此可见,复习题教学中注重选题、变题和解题.

1 选题"三原则"

1.1 要有利于解题结论和基础知识的回味

在复习题教学中教师都会自觉与不自觉地将解题基础知识或结论穿插进去.但如果照本宣科,只是将内容一一列出,全部依靠课本的现成题训练学生,不但学生却会认为这些知识已学过,还不如自己看书,感到这样上课单调乏味,提不起兴趣和积极性[4].而且也容易走向题海战术,并且难度、递度、知识板块组合不易自如调控.最终必然是将自己的教学能力定格在固有的水平上.为此施教者有责任和义务根据所用教材和所教对象的实际,适时编制添补多样化习题和多样化解答.这是机遇、也是挑战,更是使命.但有时也没有必要事必躬亲[5],事实上,除了教材以外,有些教辅用书中隐藏着不少丰富多彩的优秀典型例题习题,还有班上优秀数学学生资源的利用,等等.这些都可以帮助中等及后进学生顺利完成大学学业,消除对数学的恐惧、厌恶心理,让学生喜欢数学,不反感数学,不是因为要拿学分才学数学,而是不拿学分也要学好数学.

1.2 要有利于模式化解题的总结和提升

模式化解题是指对于一些特征性比较明显,综合性不是很强的题目,解题者在看完题目的条件与结论后,能够较快地反映出该题的解题思路,可以用什么方法求解的思维过程.思路决定出路.能否说出题目的正确思路,关键在于构思,要在构思上下功夫,在审题上做文章.解题必须先审题,审题要有好思路.因为有些数学题往往以复杂的外壳来掩盖知识的内在联系,特别是有些综合题,涉及到的知识常常改变原来的面目,例如,计算d x,虽然被积函数中有根式,但不能因式分解.比较难以抓住解题思路、主线,较难确定解题策略,或解题策略难以把握.引入辅助元素t,设,实施繁难,解题策略遇到障碍,较难自我排除.但是,如果设问题就可以得到解决,辅助元素可以是辅助未知数、辅助线、辅助问题或辅助定理等.所以抓住题目条件或结论中所涉及的知识点去构思是不能动摇的,在构思中有的需要整体分析、有的需要利用特殊、有的要结合经验联想等.

1.3 要有利于变式呈现和拓展

变式是中国传统的数学教学经验,变式教学是以培养学生的思维品质为目标,因而变式要慎之又慎.变式要把握三个度[6]:一是"梯度".变式要循序渐进,控制在学生水平的"最近发展区".让学生跳一跳才能摘到果子,否则会使学生产生畏难情绪,影响问题的解决,降低学习效率;其次是"参与度".变式不是教师的专利,要发挥学生的创新精神,体现"学为主体,教为主导".只有这样,才能调动学生的学习积极性,点燃学生的思维的火花,提高学生参与创新的意识;再次是"适度".适度包括了习题的数量、类型、难易程度,等等.变式过多过难,不但会造成题海,增加无效的劳动和加重学生的负担,而且还会使学生产生逆反心理,对变式产生厌烦情绪.但如果对复习题处理单一,局限在教材所提供的一些现成的、孤立的示例或习题上,就题论题,缺乏演变和创新,缺乏一定数量的训练.容易让学生思维模式化、套路化,这样只能培育机械模仿者;同时,也容易误导学生以为世界就那么大,题目就这几种,因而束缚学生做题可能却一错再错,使之教学效果低下.因为数学练习的次数不能代替数学变式训练的强度.因此,例题和习题的改造应成为高数教学的重要方法之一.适度的变式多解要围绕核心、提炼核心概念,呈现研究思想.这里所说的思想,不仅仅指的具体的"数学思想",还包括意义更广泛的"研究策略"、"解题策略"、"行动策略"和"哲学思想"等等[7].如何有效传授这些重要思想?首先要提炼每节课的核心问题,让学生在相关的问题及问题的解决中感悟这些思想,实现在探中思,在探中悟,在探中明.以探索发现为线索、以启迪思想开发智慧为目标,以兴趣培养为主题、让学生更喜欢数学,让教学变得更容易理解,让教学更有成效.

2 变式要多角度

2.1 变式的意义

变式主要是指对概念、公式、例题、习题进行变通推广,让学生能在不同角度、不同层次、不同情形、不同背景下重新认识的一种教学模式.数学命题、公式、定理、性质的运算,等等,是关于概念之间的关系判断,或者对某一事物的概括,是一个逻辑真命题,是数学家通过研究发现的数学结论.变式教学可以通过改变概念的外延或改变一些能混淆概念外延的属性来获得对概念的多角度理解,还可以通过数学活动操作帮助学生理解概念产生发展的原因,获得解决问题的表征和策略,设置层次性的概念模型促进概念的形成铺垫层次化的问题串以形成解题策略.例如,罗尔定理可推导拉格朗日中值定理,但罗尔定理是拉格朗日中值定理的特殊;拉格朗日中值定理可推柯西中值定理、泰勒中值定理,同时,拉格朗日中值定理是柯西中值定理和泰勒中值定理的特殊.定理的特定条件的改变,定理的结论也随着改变,即得不同的变式.老师要改变观念,不是不允许学生自己变题,而是要提倡他们自己变题;不是压抑他们自己变题,而是推动他们自己变题;不是听任他们自己信马由缰,而是导之开之.

恰当合理的变式能营造一种生动活泼、宽松自由的氛围.变式要有"梯度"、"适度"和"参与度".现从基本公式算变式(2)开始拓展,设计一套层次性递进的数学计算题变式.计算变式(1)在这常用公式变化的过程中,揭示了一类问题的本质特性,学生从公式到简单模仿到寻求"几种特殊类型函数的积分"的方法.这样的拓展让学生始终兴趣盎然,感到学习紧张有趣.进行局部探究,不仅使学生进一步加深了对公式的理解和灵活应用,而且拓展了复习题内容的深度和广度.

2.2 一题多变,变通概念公式与各知识的纵横联系

现以同济大学数学系主编的高等数学(第六版)上册,第221页总复习题四的第40题为例.此题是较典型的三角函数的有理式积分,三角函数有理式是指由三角函数和常数经过有限次四则运算及乘方运算所构成的函数.此题从形式上看较为浅显,但适当变形拓展,或分解,重新组合,引导学生深层次的探索,就能感受到此题的内涵.

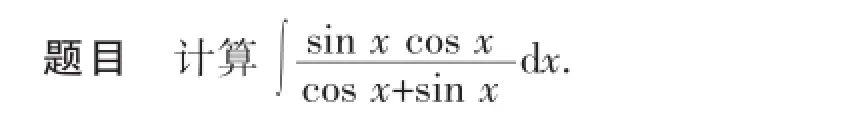
怎样从学生已有的知识和经验出发,最大限度启发引导获取新知识是关键.被积函数是三角函数有理式,即分式.分式中含有sin x,cos x的同角三角函数的有理式,被积函数虽然只有两个有理式,但较难凑出积分.寻找分式中的分子与分母之间的联系是关键,分子、分母分别是这两个同角正余弦有理函数的积与和.抓住"同角"的特征,利用"同角"三角函数的关系式,变通分母,可以凑出分子有理函数的积.即(sin x+cos x)2=1+2sin x cos x,先用sin2x+cos2x=1导入,后把cos x+sin x转化成

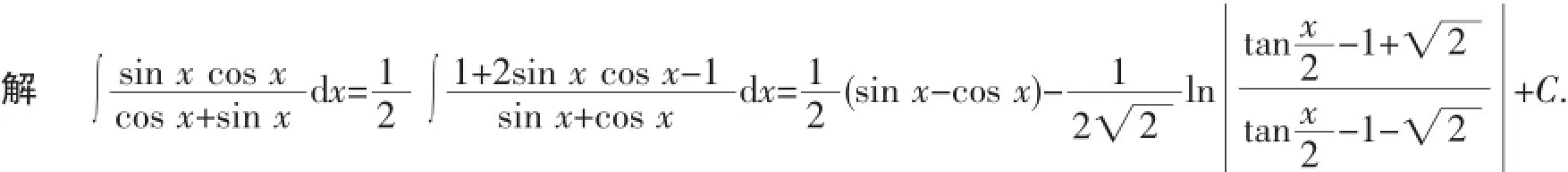
为了给学生的研究提供支持,给他们的学习牵马引镫,提供他们自己学的更为有利条件,为学生准备,为学生激励,为学生做加油站[8].课堂以轻松、有趣的方式引入问题吸引学生的注意力,是激发学生学习兴趣的有效方法[9].如果把被积函数中的分母sin x+cos x变为1+sin4x,分子不变.即:

这个变式的设置在学生的最近发展区,学生感兴趣,有的说计算的关键是把被积函数转化为基本积分公式,有的说变被积函数中的分母和分子,教师抓住学生思维"固定点"点拨,转化为哪个基本公式,怎样转化?怎样变分子和分母?学生即刻说出:分母1+sin4x=1+(sin2x)2,分子sin x cos x=所以,原式arctan sin2x+C.

变更问题,诱发灵感[8].问题的动态生成是新课程倡导的一个重要的教学理念和努力追求的目标.怎样追求?就原题目而言,微变一下,把被积函数中的分子sin x cos x,变为sin x,分母不变."变式到"基本的命题,即:

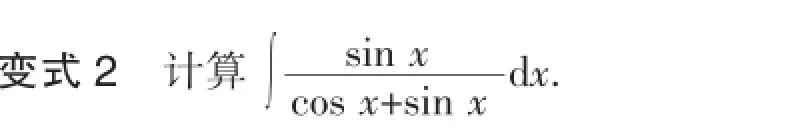
这是一个基于比原题目简便的计算,不仅能够回顾和复习基本概念和基本方法,而且能不断地激发学生的智慧潜能,将学生的思维引向数学的基本概念和基本思想,能使学生养成良好的思考问题的习惯,以 "不变"的思考问题的出发点来应对"万变"的数学题目.先变更被积函数中的分子,sin x=[(sin x+cos x)+ (sin x-cos x)],然后分解,求两个积分的差.

2.3 一题多解,促进解题策略的逐步优化

为了知识方法的理解和智慧的获得,需要进行技能的训练和问题的解决.适用一题多解或多题一解的方法,不但可以帮助学生获得问题解决的特定经验,而且可以促进解题策略的逐步优化.仍以2.2中的题目为例,可变式如下.

变式3也是一道难得的好题,涉及到三角、导数和积分的基本公式.学生通过类比、分析、归纳、相互交流和互动,得出了如下解析.

解析1先将被积函数进行恒等变形,再利用正、余弦函数的导数关系式解之.即

解析2把被积函数中的分子分母同乘以cos x-sin x,用同角三角函数的关系式、半角公式、二倍角公式,凑出新的微分,用微分基本公式计算.

解析3被积函数的分子分母同乘以cos x+sin x,用同角三角函数的关系式、半角公式、二倍角公式凑出新的微分,用微分基本公式计算.

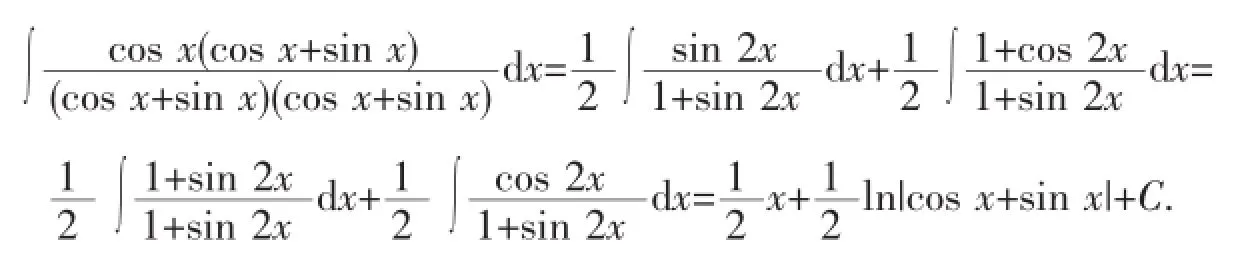
解析4把变式2中被积函数的分子、分母同除以cos x≠0,得2tan x d(tan x),1+tan2x=sec2x,把被积函数是难点,将被积函数向积分公式靠拢.即:

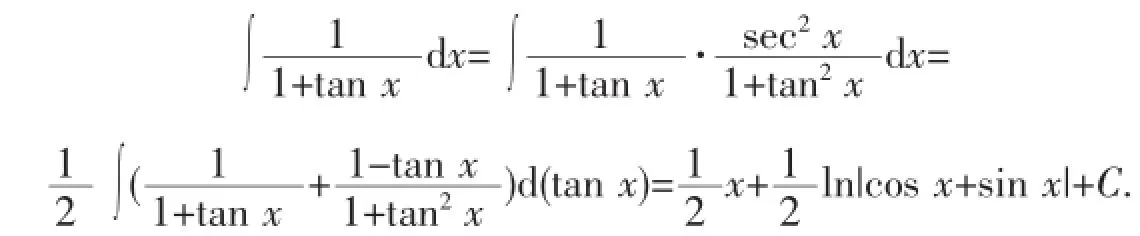
解析5变式2的被积函数中分母有sin x,分子没有sin x,通过在分子中加上sin x-sin x来转化,被积函数中的分母的微分正好是分子,凑出新的积分,然后再在分式中的分子加上cos x-cos x,这是有技巧性的层次性探索.但技巧有其局限性,适用的范围比较狭窄.

解析6运用"万能代换"法,设tan也可方便地解题.

以上6种解析,不同程度的诱发了学生灵感,开拓了学生思维,化解了教学难点,降低了学习难度,提高了学习效益,梳理了知识网络.

3 结语

数学教学倡导把例习题的变式多解当作"数学研究"的主要手段之一,变式多解应结合教材内容和学生实际,拓展和改造的题目应是在教师的启发和引导下由学生讨论完成,拓展和改造要建立在学生现有的认知水平上.拓展和改造不仅是一个教师学识认知系统化、思想化的过程,而且也是一个数学知识再创造的过程,一个教学内容艺术化的过程[9].由联想所学知识,运用数学思想方法,确定解题切入点、监控调节点、审视解题反思点,不断由低级向高级逐步抽象的复杂心理过程,因而选题、变题、解题者在选、变、解题过程中的思维过程逐步由数学知识、方法这些相对具体的层面,向数学概念、公式、解题策略等更为抽象的层次发展.以使选题、变题、解题能从更高的观点、更宽的视野,更理性的眼光,去思考数学,领悟数学的哲理[10].

教学中,有意识暴露一些题目变式的思维过程,并让学生参与变式编拟和求解变式问题可以收到更好的效果:一是揭示了一类问题的本质特性,拓宽了复习内容的深度和广度,实现了基本方法的灵活应用;二是促进了解题策略的逐步优化,减少复习的随意性和盲目性;三是彰显了学生个性,展示了学生才能,满足了个性化教育的需要;四是提供了一个表达并反思自己独特的关于数学的情感,知识,方法和观念的空间,促进了元认知能力的发展;五是创造了师生对话交流的新途径,构建了一种和谐教育环境;六是丰富了数学文化生活,提供了一个传播数学文化的载体;七是关注了学生数学发展的不同需求,为不同学生提供不同的发展空间,为促进学生个性和潜能发展搭建了新的平台;八是加强了问题解决过程中的认知提升和情感培养,不断深挖了学生深度的思维;九是巩固和深化了新知,补充与延伸新知,综合运用新知,领悟数学思想与方法.

[1]刘键.课本习题改造是"数学探究"的重要渠道[J].数学通报,2006(8):33-34.

[2]吴立宝.中澳数学教科书习题的比较研究---以人教版和HMZ8年级教科书为例[J].数学教育学报,2013,22(2):58-64.

[3]李静,王秀兰.本原性问题驱动下的高等数学变式教学[J].数学教育学报,2013,22(6):94-97.

[4]俞新龙.谈谈高三复习课中例题的选择[J].数学教学,2007(10):5-8.

[5]马建龙.编制变式题组,功克学习难关[J].数学通报,2013(5):27-30.

[6]吴莉霞,刘斌.变式教学要把握三个"度"[J].数学通报,2006(4):18-19.

[7]王克亮.在问中悟,在问中探,在问中明[J].数学通报,2013(9):38-40.

[8]郭思乐.以生为本的教学观:教皈依学[J].课程.教材.教法,2005,25(12):14-22.

[9]王钦敏.如果对教材进行有益的改造[J].数学通报,2013(1):45-48.

[10]单墫.数学是思维的科学[J].数学通报,2001(6):1-3.

On them ultip le solutions to a review question's variant

QIU Yun-lan
(Mathematics Departmentof Shaozhou Normal College,Shaoguan University, Shaoguan 512009,Guangdong,China)

Higher mathematics classroom teaching core mission is to develop students'thinking ability to explore the subjectwhich lies in the improvement ofmathematical thinking ability to explore the topic,variant, and improving the quality of problem-solving,rather than the increasing of topics,variantand solving.Problemsolving should be in line with three principles and diversified,which better connects the horizontal and vertical knowledge to optimize the solving strategies,which foster the thinking,analyzing and solving abilities of the students.

highermathematics;variant teaching;problem-solving approach;exploring ability

G642.4

:A

:1007-5348(2014)06-0087-05

(责任编辑:邵晓军)

2014-03-26

邱云兰(1956-),男,广东乐昌人,韶关学院韶州师范分院数学系副教授,主要从事数学教育教学的实践与研究.