巨灾债券定价参数敏感性分析——以我国洪水灾害为例*
2014-02-10邢天才康晗彬
邢天才,康晗彬
(东北财经大学金融学院,辽宁 大连 116025)
巨灾债券定价参数敏感性分析
——以我国洪水灾害为例*
邢天才,康晗彬
(东北财经大学金融学院,辽宁 大连 116025)
巨灾债券是巨灾风险转移资本市场上交易最活跃、使用最广泛的金融创新产品,其定价涉及的影响因素较为复杂。本文基于资产、负债和利率理论引入巨灾债券定价模型,并以我国洪水灾害为例对模型参数敏感性进行了分析,分别研究了触发水平、利率期限和资产负债比对巨灾债券定价的影响规律。参数敏感性研究结果表明:巨灾债券价格随触发水平、资产负债比的提高而增大,随利率水平的提高而降低;我国洪水灾害债券适宜的触发水平在万亿元量级,这主要是由我国洪水灾害损失分布决定的。本文研究对于我国巨灾债券发行具有精算定价及政策指导等参考作用。
巨灾债券定价;资产负债比;参数敏感性;蒙特卡罗模拟方法
策研究。E-mail:xingtiancai@126.com
康晗彬 (1976-),女,辽宁鞍山人,博士研究生,主要从事巨灾风险管理与保险精算研究。E-mail:hbkang2007@hotmail.com
一、引 言
我国是世界上自然灾害最严重的国家之一,其中洪水灾害导致的经济损失位居首位,大约2/3的国土面积有着不同类型和不同危害程度的洪水灾害。面对我国重大的洪水灾害损失,单纯依靠保险市场很难有效分散洪水灾害风险,有必要借鉴发达国家的成功经验,借助资金雄厚的资本市场发行巨灾证券以分散巨灾风险。巨灾债券是当前国际金融市场上应对巨灾风险最为典型的巨灾风险证券化产品,其定价机制是国内外研究者关注的焦点。早期,Cummins和 Geman[1]、Louberge 等[2]、Briys[3]、Cox 和 Pedersen[4]在利率期限结构和巨灾风险概率结构基础之上,讨论了巨灾债券的均衡和无套利定价模型;Lee和Yu[5]在分别考虑违约风险、道德风险和基差风险的前提下采用蒙特卡罗模拟方法对巨灾债券定价进行了研究;Vaugirard[6]利用套利方法对巨灾债 券 定 价 进 行 了 研 究;Morton[7]、 Wang[8]、Christofides和 Smith[9]与 Christofides[10]分别提出了具有代表性的巨灾债券定价模型;Egami和Young[11]、Jarrow[12]以及 Zhu[13]又做出了进一步研究。
在巨灾债券定价机制中,触发事件和利率期限结构是影响其价格水平的重要因素。近年来随着水文学研究的不断深入,能够更准确地估计洪水灾害损失、确定触发事件水平。李永等[14]进行了多事件触发巨灾债券设计与定价研究。债券的利率期限结构模型主要分为静态模型和动态模型两种。在金融市场发达的国家,动态利率模型广泛地用于固定收益证券和利率衍生品及含有嵌入期权的金融衍生品的定价分析,如巨灾债券可以视为债券和嵌入期权的合成。其中较为典型的动态利率模型包括Vasicek模型[15]、CIR随机利率模 型[16]和 CKLS 模 型[17]。Poncet 和 Vaugirard[18]使用了HJM和CIR随机利率模型 (以下简称CIR模型)在巨灾衍生品定价中,比较了两种利率模型对价格的影响。
本文拟在资产负债管理基础上,运用蒙特卡罗模拟方法对巨灾债券定价进行模型研究,并以我国洪水灾害为例对模型参数敏感性进行分析,重点研究资产负债比、触发事件水平和利率水平等参数对巨灾债券定价的影响规律。
二、巨灾债券定价理论模型
巨灾债券通常是由 (再)保险公司或SPV(特殊目的机构)发行。SPV是再保险公司为发行巨灾债券而成立的特殊目的机构,一方面它受(再)保险人的委托发行债券来分散风险、筹集资金;另一方面它又肩负着在约定条件下向(再)保险人进行赔付的义务。本文所述的资产、负债、利率和累计损失动态模型涵盖了以上机构,具有普遍性并且采用风险中性定价措施,其模型构建主要基于Lee和Yu[5]的资产负债模型并进行了改进。Lee和 Yu[5]提出的巨灾债券模型假设 (再)保险公司或SPV负债在整个债券发行期内保持不变,而本文拟采用负债—利率动态模型来描述债券发行期内负债的动态变化。
(一)资产、负债动态理论模型
资产负债管理是一种协调资产与负债决策的管理活动,是一个持续完善和调整的动态过程,因此本文采用资产负债动态模型。
1.资产动态模型
在考虑资产价值问题时,除了典型的维纳过程外,还要考虑随机利率的影响,因为其在巨灾债券发行人投资固定收益中占很大比重。巨灾债券投资中非常注意收益高、利息率敏感的商业票据和国债等投资。考虑随机利率影响的巨灾债券发行人资产价值模型如下式所示:



本文利率模型采用CIR模型,它是在连续时间框架下利用一般均衡方法构建的利率期限结构模型。同Vasicek模型相比,其优势是可避免负利率的产生。CIR模型如下式所示:

其中,k表示平均回弹系数;m表示长期利率均值;υ表示利率的波动性参数;Zt表示利率模型维纳过程,它独立于上述资产模型维纳过程WV,t。结合 (1)和 (2)式 (再)保险人的资产动态模型表示为:

其中,参数λr表示利率风险市场价格,在CIR模型中是常量;Z*t表示风险中性测度Q下的维纳过程。由此资产动态模型经过风险中性定价改变为:

2.负债动态模型
本文的负债定义为巨灾债券发行人的巨灾债券偿付额与其他未来赔付额之和的现值,其动态模型如下式所示:


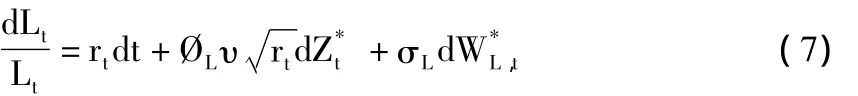
(二)巨灾累计损失动态模型

(三)巨灾债券定价模型
在风险中性世界中,通过各种情境下的赔付期望贴现值来计算巨灾债券价格。本文以一年期无中间给付的巨灾债券为例,给出不考虑风险因素和考虑违约风险因素的巨灾债券定价,其模型建立主要基于Lee和Yu[5]的相关研究。
1.不考虑风险因素的巨灾债券定价
不考虑风险因素的巨灾债券在成熟期T时的赔付额可表示为:

其中,K表示巨灾债券的触发水平;CT表示到成熟期的累计损失;rp表示当累计损失到达触发水平K时,债券持有人得到的本金赔付比例;L表示债券发行人总负债的面值;α表示巨灾债券面值占总负债面值的比例。由此,根据风险中性定价措施Q,巨灾债券价格在发行初期(t=0)可表示为:


2.考虑违约风险因素的巨灾债券定价
巨灾债券通常是指投资在可信任的基金、以偿付有限索赔和归还本金给债券持有者为目的的债券。在巨灾债券发行人破产或违约时,巨灾债券持有人同其他债券持有人相比具有优先权;如果巨灾债券发行人没有破产,当潜在损失低于触发水平时,债券持有者能得到巨灾债券的所有本金;否则他们只能被偿还部分本金。因此考虑违约风险时巨灾债券的违约风险赔付额表示为:

其中,POi,T表示到期时根据实际损失对巨灾债券的赔付额;Vi,T表示到期时债券发行人的资产价值;Ci,T表示到期时债券发行人的累计损失;L、α、K和rp定义与前述相同。
根据巨灾债券的偿付结构和资产、利率动态模型,巨灾债券定价可表示为:

三、数值模拟结果与分析
将本文资产负债动态模型与各种情境下的巨灾债券赔付额模型相结合,再考虑我国洪水灾害的损失程度和频率分布,即可在资产管理视角下对不同风险因素作用下的巨灾债券进行精算定价研究和模型参数敏感性研究。本文采用《中国财产保险重大灾因分析报告 (2008)》[19]中1990—2008年我国洪水灾害实际损失数据进行统计。我国洪水灾害损失程度服从对数正态分布,频数符合负二项分布,即ct洪水和N(t)洪水可表示为:

我国洪水灾害年损失额分布统计直方图和累计概率图如图1所示,其年损失额均值为4.41×1011元。

图1 我国洪水灾害年损失额分布统计直方图和累计概率图
本文巨灾债券定价估值采用蒙特卡罗模拟方法,并利用Matlab软件编程实现。模拟过程假设洪水巨灾债券的发行期是一年,一星期为基础单位,每一基础单位都运行20 000次,具体模拟计算步骤参见康晗彬和邢天才的相关研究。模型相关参数初值如表1所示,运用该模型参数分别对不考虑风险因素、考虑违约风险的巨灾债券定价进行了数值模拟与分析比较,基于我国洪水灾害的损失程度和频率分布研究触发水平、利率期限和资产负债比等模型参数对巨灾债券定价的敏感性。

表1 模型参数意义及赋值
(一)触发事件水平对洪水巨灾债券定价的敏感性分析
巨灾债券触发事件是决定对巨灾损失是否进行赔付和赔付多少的标尺,是巨灾债券区别于资本市场的其他类型债券的核心特征,也是影响巨灾债券能否发行成功的决定因素。单一触发事件的巨灾债券和多触发事件的巨灾债券各有优劣。发起人一般会希望一只债券中包括的风险事件越多越好,这样不仅能有效地降低交易成本,而且能使不同区域的巨灾事件共享保障限额;投资者则正好相反,他们更倾向于单一事件触发机制的债券,因为单一事件触发机制能使他们更容易根据自己的投资组合偏好对特定巨灾风险进行评估。
本文研究实际损失触发事件K对我国洪水巨灾债券的无风险、考虑违约风险两种情境下定价的影响规律。由表2模拟结果可以看出,随着触发事件K的增大,无风险、考虑违约风险情境下巨灾债券定价均不断提高。这主要是由于随着触发事件K的不断增大,洪水巨灾债券对发生巨灾损失赔付的概率降低,使投资者更愿意购买洪水巨灾债券,从而使洪水巨灾债券的价格越来越高。模拟结果表明,我国洪水巨灾债券适宜的触发事件K在万亿元量级,相应的洪水巨灾债券发行人的负债规模也在该量级上。此外,从表2还可以看到,违约风险因素对洪水巨灾债券的价格有显著影响且使洪水巨灾债券价格降低,尤其是在洪水巨灾发生概率高的情况下。

表2 触发事件K的敏感性分析
(二)利率模型参数对洪水巨灾债券定价的敏感性分析
本文假设发行的洪水巨灾债券是一年期零息债券,当T=1时,由 (11)、(12)、(13)式

图2 初始瞬时利率r0和长期利率均值m为5%的BCIR(0,T)分布
2013年我国发行的国债一年期利率达到7.1%,以此为依据,本文对初始瞬时利率r0和长期利率均值m分别赋值为5%、6%、7%和8%,研究利率参数对考虑违约风险情境下洪水巨灾债券定价的敏感性分析。由表3可以看到,当资产负债比为1.1、触发水平为10万亿元规模时,违约风险情境下初始瞬时利率r0与长期利率均值m为5%时洪水巨灾债券定价Pi(0)=0.8893、初始瞬时利率r0与长期利率均值m为8%时Pi(0)=0.8633;当初始瞬时利率r0与和表1的赋值可以得到A(t,T)和B(t,T)为常数,所以可计算得到无风险零息债券价格BCIR(0,T)也近似为常数。根据本文前述洪水巨灾债券的发行期是一年,一星期为基础单位,每一基础单位都运行20 000次。图2和图3分别给出初始瞬时利率r0和长期利率均值m为5%和8%时,BCIR(0,T)值与时间 (周)的相互关系图。由图2和图3可见,当初始瞬时利率r0和长期利率均值m为5%时,无风险零息债券价格BCIR(0,T)分布区间为 (0.9513,0.9555),其均值为0.9537;当初始瞬时利率r0和长期利率均值m为8%时,无风险零息债券价格BCIR(0,T)分布区间为 (0.9232,0.9275),其均值为0.9252。长期利率均值m为6%、触发水平为10万亿元规模时,违约风险情境下资产负债比为1.1时洪水巨灾债券定价Pi(0)=0.8806、资产负债比为1.4时Pi(0)=0.8916。由此可见,当初始瞬时利率r0与长期利率均值m逐步增大时,考虑违约风险的洪水巨灾债券价格逐步降低,这一结论也正符合零息债券的特点。由表3同时可以看出,洪水巨灾债券价格随资产负债比的提高而增大,表明有效的资产负债管理可以分散违约风险。

图3 初始瞬时利率r0和长期利率均值m为8%的BCIR(0,T)分布

表3 违约风险情境下洪水巨灾债券定价的利率敏感性分析
四、结论与建议
本文基于资产、负债和利率理论引入巨灾债券定价模型,并以我国洪水灾害为例对触发水平、利率期限、资产负债比等模型参数的敏感性采用蒙特卡洛方法进行了数值分析。模拟结果表明:第一,我国洪水巨灾债券适宜的触发机制K在万亿元量级,相应的洪水巨灾债券发行人的负债规模也在该量级上,这主要是由我国洪水巨灾损失程度和频数分布决定的。第二,洪水巨灾债券价格随触发水平的提高而增大,随利率水平的提高而降低。第三,洪水巨灾债券价格随资产负债比的提高而增大,表明有效的资产负债管理可以分散违约风险。
本文研究对于我国洪水巨灾债券发行具有精算定价及政策制定参考作用。第一,本文应用CIR模型可以有效贴近现实利率、避免负利率的产生,从而提高定价结果的合理性,因此洪水巨灾债券发行主体 (SPV)在进行债券定价时,需要合理选择利率期限模型并提高模型参数的合理性,从而控制利率模型带来的定价偏离。第二,本文在资产负债视角下对我国洪水巨灾债券的单一事件触发机制的量化研究表明,监管机构应加强对SPV资产负债状况的监管,SPV应通过有效的资产负债管理提高其所发行洪水巨灾债券在资本投资市场的吸引力和竞争力。
[1]Cummins,D.J.,Geman,H.Pricing Catastrophe Insurance Futures and Call Spread:An Arbitrage Approach[J].The Journal of Fixed Income,1995,(4):46-57.
[2]Louberge,H.,Kellezi,E.,Gilli,M.Using Catastrophe-Linked Securities to Diversify Insurance Risk:A Financial Analysis of CAT Bonds[J].Journal of Insurance Issues,1999,22(2):125-146.
[3]Briys,E.From Genoa to Kobe:Natural Hazards,Insurance Risks and the Pricing of Insurance-Linked Bonds [M]. London: Lehman Brothers International,1997.
[4]Cox,S.H.,Pedersen,H.W.Catastrophe Risk Bonds[J].North American Actuarial Journal,2001,4(4):56-82.
[5]Lee,J.P.,Yu,M.T.Pricing Default- Risky Cat Bonds with Moral Hazard and Basis Risk[J].Journal of Risk and Insurance,2002,69(1):25-44.
[6]Vaugirard,V.E.Pricing Catastrophe Bonds by an Arbitrage Approach[J].The Quarterly Review of Economics and Finance,2003,43(1):119-132.
[7]Morton,N.L.Pricing Risk Transfer Transactions[Z].Porto Cervo:The 31th ASTIN Colloquium,2000.
[8]Wang,S.S.Cat Bond Pricing Using Probability Transforms[R].Geneva Papers,2004.
[9]Christofides,S.,Smith,A.D.DFA - The Value of Risk[Z].Meyers:CAS Forum,2001.
[10]Christofides,S.Pricing of Catastrophe Linked Securities [Z]. Bergen: The 35th ASTIN Colloquium,2004.
[11]Egami,M.,Young,V.R.Indifference Prices of Structured Catastrophe(CAT)Bonds[J].Insurance:Mathematics and Economics,2008,42(2):771-778.
[12]Jarrow,R.A.A Simple Robust Model for Cat Bond Valuation [J].Finance Research Letters,2010,7(2):72-79.
[13]Zhu,W.G.Ambiguity Aversion and an Intertemporal Equilibrium Model of Catastrophe-Linked Securities Pricing[J].Insurance:Mathematics and Economics,2011,49(1):38-46.
[14]李永,范蓓,刘娟.多事件触发巨灾债券设计与定价研究:以中国台风债券为例[J].中国软科学,2012,(3):41 -48.
[15]Vasicek,O.An Equilibrium Characterization of the Term Structure [J].The Journal of Financial Economics,1977,5(2):177 -188.
[16]Cox,J.C.,Ingersoll,J.E.,Ross,S.A.A Theory of the Term Structure of Interest Rates[J].Econometrica,1985,53(2):385 -467.
[17]Chan,K.C.,Karolyi,A.G.,Longstaff,F A.,Sanders,A.B.An Empirical Comparison of Alternative Models of the Short- Term Interest Rate[J].The Journal of Financial Economics,1992,47(3):1209-1227.
[18]Poncet,P.,Vaugirard,V.E.The Pricing of Insurance Linked Securities under Interest Rate Uncertainty[J].Journal of Risk Finance,2002,3(3):48 - 59.
[19]王银成,王和,李秀芳,等.中国财产保险重大灾因分析报告(2008)[M].北京:中国财政经济出版社,2009.
[20]康晗彬,邢天才.考虑多风险因素的我国巨灾债券定价研究[J].保险研究,2013,(8):94-106.
(责任编辑:韩淑丽)
F830.9
A
1000-176X(2014)05-0059-06*
2014-02-16
邢天才 (1961-),男,山东青岛人,教授,经济学博士,博士生导师,主要从事金融市场监管、保险经济与政
·金融与投资·
