关于丢番图方程x3±1=pD1 y2

杜先存，万 飞，赵金娥

方程x3±1=Dy2(D是无平方因子的正整数)是一类重要的丢番图方程，其整数解已有不少人研究过.柯召、孙琦［1］证明了当D不含3或6k+1型的素因子时，方程x3±1=Dy2无整数解，但当D含6k+1型的素因子时，方程的求解较为困难.乐茂华［2－3］证明了 p为12s2+1(s∈ Z+)型素数时，方程x3± 1=3py2无正整数解.张淑静［4－5］证明了 D1=2αq，α =0 或 1，p，q均为奇素数，p=12r2+1(r∈Z+)，q≡5(mod 6)时，方程 x3± 1=3Dy2无正整数解;D=2αpq，α =0 或 1，p、q均为奇素数，p=3(24r+19)(24r+20)+1(r∈Z+)，q≡5(mod 6)时，方程x3±1=3pD1y2无正整数解.张淑静、袁进［6］证明了D=D1p，D1不能被3或6k+1型的素数整除，p=3(24r+19)(24r+20)+1(r∈Z+)为素数时，方程x3±1=Dy2无正整数解.在此基础上，论文主要讨论p为6k+1型的素因子时，方程

的解的情况.

1 相关引理

引理1［7］设 a ＞ 1，(a，b)∈ N2，ab不是完全平方数，如果 ax2－ by2=1 有解(x，y)∈ N2，设x1+y1是方程ax2－by2=1(x，y∈Z)的基本解，则ax2－by2=1的任一组解可以表示为

引理 2［8］若 p=3t(t+1)+1(t∈ N)，则

的最小解为(2，2t+1).

2 主要定理及证明

定理1 设D1是不能被3或6k+1型的素数整除的无平方因子的正整数，D1≡7(mod 12)，p=3(12s+k)(12s+k+1)+1(k=4，7，s∈N)为素数，则丢番图方程

无正整数解.

证明 设(x，y)是方程(3)的正整数解，故

又x2－x+1的素因数必为3或形如6k+1的素数，而D1是不能被3或6k+1型的素数整除的正整数，故由文［6］的定理1的证明过程可知，(3)可分解为以下两种情形:

情形Ⅰ:x+1=D1u2，x2－ x+1=pv2，y=uv，gcd(u，v)=1.

情形Ⅱ:x+1=3D1u2，x2－ x+1=3pv2，y=3uv，gcd(u，v)=1.

对于情形Ⅰ，由D1≡7(mod 12)，得D1≡－1(mod 4).

又由

可得

故

又

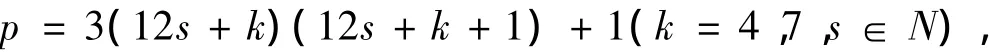
则p≡1(mod 4).又pv2为奇数，故v2为奇数，所以v2≡1(mod 4)，则有

又

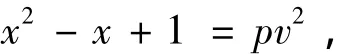
则

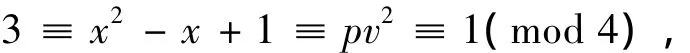
矛盾，所以情形Ⅰ不成立.

对于情形Ⅱ，将第一式代入第二式，整理得

则(2v，2D1u2－1)是方程(5)的一组解.因为

则由引理2，得(2，24s+2k+1)是方程(4)的最小解.

由引理1知，由(4)式可得

由(5)式可得

又 k=4，7 时，3|(24s+2k+1)，所以

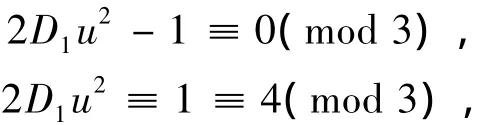
故

又 D1≡7(mod 12)，得 D1≡1(mod 3)，故

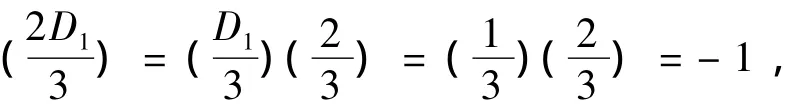
矛盾.由此可知，情形Ⅱ不成立.

综上，方程(3)在题设条件下无正整数解.

定理2 设D1是不能被3或6k+1型的素数整除的无平方因子的正整数，D1≡1，7，10，19(mod 24)，p=3(24s+k)(24s+k+1)+1(k=4，19，s∈ N)为素数，则丢番图方程

无正整数解.

证明同定理1，此略.

定理3 设D1是不能被3或6k+1型的素数整除的无平方因子的正整数，D1≡5(mod 12)，p=3(12s+k)(12s+k+1)+1(k=4，7，s∈N)为素数，则丢番图方程

无正整数解.

证明 设(x，y)是方程(7)的正整数解，故

又x2+x+1的素因数必为3或形如6k+1的素数，而D1是不能被3或6k+1型的素数整除的正整数，由文［6］的定理1的证明过程可知，(4)可分解为以下两种情形:

情形Ⅲ:x － 1=D1u2，x2+x+1=pv2，y=uv，gcd(u，v)=1.

情形Ⅳ:x － 1=3D1u2，x2+x+1=3pv2，y=3uv，gcd(u，v)=1.

对于情形Ⅲ，由x－1=D1u2，可得

而 u2≡ 0，1，4(mod 8)，故

所以

又 D1≡5(mod 12)，得 D1≡1，5(mod 8)，所以

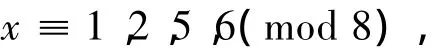
则

综上，当D1≡5(mod 12)时，有

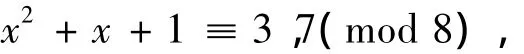
又

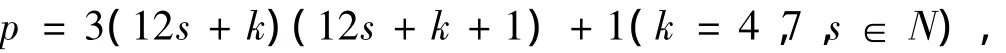
故p≡1，5(mod 8).又pv2为奇数，故v2为奇数，所以v2≡1(mod 8)，则

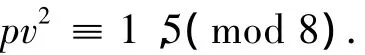
又 x2+x+1=pv2，则

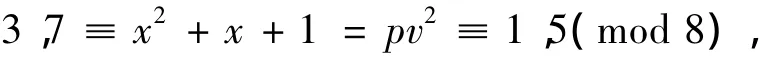
矛盾，所以情形Ⅲ不成立.

对于情形Ⅳ，将第一式代入第二式，整理得

则(2v，2D1u2+1)是方程(8)的一组解.因为

则由引理2，得(2，24s+2k+1)是方程(8)的最小解.

由引理1知，从(8)式可得

由(9)式可得

又 k=4，7时，3(24s+2k+1)，所以

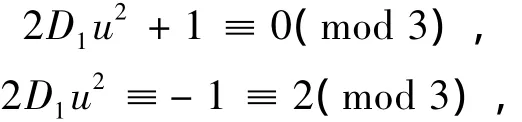
有

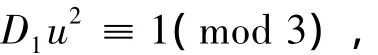
又D1≡5(mod 12)，得 D1≡2(mod 3)，故=－1，矛盾.由此可知，情形Ⅳ不成立.

综上，方程(4)在题设条件下无正整数解.

定理4 设D1是不能被3或6k+1型的素数整除的无平方因子的正整数，D1≡－1，5，14，17(mod 24)，p=3(24s+k)(24s+k+1)+1(k=4，19，s∈ N)为素数，则丢番图方程

无正整数解.

证明同定理3，此略.

［1］ 柯召，孙琦.关于丢番图方程 x3±1=Dy2［J］.中国科学，1981，24(12):1453 －1457.

［2］ 乐茂华.关于Diophantine方程x3+1=3py2［J］.保定师范专科学校学报，2004，17(2):12－13.

［3］ 乐茂华.关于Diophantine方程x3－1=3py2［J］.广西师范学院学报:自然科学版，2005，22(4):22－23.

［4］ 张淑静.关于 Diophantine方程 x3±1=3Dy2［J］.高师理科学刊，2009，29(2):16 －18.

［5］ 张淑静，杨雅琳，贾晓明.关于Diophantine方程x3±1=3pD1y2［J］.山西师范大学学报:自然科学版，2009，293(4):31－33.

［6］ 张淑静，袁进.关于 Diophantine方程x3±1=Dy2［J］.曲阜师范大学学报:自然科学版，2009，35(42):47－49.

［7］ 夏圣亭.不定方程浅说［M］.天津:天津人民出版社，1980:97－98.

［8］ 杜先存，史家银，赵金娥.关于不定方程x3－1=py2［J］.西南民族大学学报:自然科学版，2012，38(5):748－751.