让枯燥无味的数学变得“有趣、有味、有惑”——Matlab中的音乐合成

易昆南， 李 慧， 赵澍源

(中南大学 数学与统计学院，湖南 长沙 410075)

0 引 言

如何在实验中提高学生综合素质与创新能力[1]？兴趣是最好的老师。学生没有学习兴趣，就不可能有学习积极性，当然更谈不上进一步提高学生的数学素质。我们在Matlab实验教学中，通过“音乐与数学有关吗？”问题的精心设计，把一个基础性、验证性实验转变成设计性、综合性实验，让学生真正感悟到数学无处不在，数学大有用武之地。数学建模大有作为。

1 兴趣入手做验证性实验

从人才能力结构的组成来看，基础性、验证性实验侧重于对理论知识的理解和记忆；设计性、综合性实验则要求学生在扎实的理论基础上拓宽知识面，培养较强的实验动手能力和分析、解决问题的能力。所以，从本质上说，实验本身就是一种创新活动。对于基础性、验证性实验强调学生自己动手。为此，介绍了声音的构成的三要素[2]，即声音频率决定音调；声音振幅决定音量；声音谐波决定音色。 音乐是一系列振幅和频率不一的正弦波叠加形成的！为验证这一说法，从兴趣入手让学生做如下验证性实验。

步骤1：下载mp3格式的贝多芬《月光曲》[3]。

步骤2：下载音频转换器，将mp3格式的《月光曲》转换为wav格式 。

步骤3：wavread调入wav格式的《月光曲》，wavplay语句在Matlab中播放。

步骤4：对wavread调入的数据作图。

结果是一边可以听到一段美妙的《月光曲》音乐，一边可以观察到音乐信号是由一系列振幅和频率不一的正弦波叠加且带有不同包络[4]修饰形成的。极大地提高了学生想进一步探索的实验的积极性。

2 实验中创新素质的培养

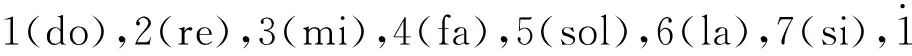
1,21/6,21/3,25/12,27/12,23/4,211/12,2

学生以此作为频率，确定音高，就可以组成乐音的各级音阶。

进一步，每个指定音调的唱名都对应固定的基波信号频率[6]。所谓唱名是指平日读乐谱唱出的1(do) 、2(re)、3(mi) ……, 每个唱名并未固定基波频率。当指定乐曲的音调时才知道此时唱名对应的频率值。如C调“1(do)”的基波频率为261.63 Hz, F调“1(do)”的基波频率为174.61Hz。 那么，F调的故各音的频率又是多少？学生思考后也给予回答：

1(do)，2(re)，3(mi)，4(fa)，5(sol)，

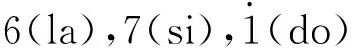
对应的频率为：

174.610 0 195.993 1 219.994 8 233.076 4

261.619 4 293.657 8 329.619

3 教师指导是关键

由于声音谐波[7]决定音色，在音乐领域中称谐波为“泛音”[8]，由谐波产生的作用称为音色变化。当指定音调之后，仅指定了乐音信号的基波频率，谐波情况并未说明。各种乐器，如钢琴或单簧管，都可以发出某一音调下的唱名，而人的听觉会明显感觉两者不同，这是由于谐波成分有所区别，频谱[9]结构各异。

由于在一定条件下，任何周期信号都可以展开为三角型傅里叶级数[10]，作为音乐信号也不例外，即周期信号f(t)可表示为：

φn)

图1 傅里叶级数逼近的方波

f(t)与An、φn有一一对应的关系，依据An、φn作出的图称为频谱图[11]。要完成各种乐器发出声音的音色的模拟，只需录制各种乐器的声音信号，通过傅里叶级数变换，获得对应的频谱图，就可以模拟还原该乐器奏出的声音。

介绍了音乐合成的原理，提供了如何使用Matlab中的傅里叶级数变换的工具[12]，在教师的指导下，以学生为主体，学生根据研究课题规定的任务，自己主动去探索、去发现各种乐器的傅里叶级数变换的频谱图，自己用曲线拟合的方法去获得各种乐器的包络。教师引导学生按下述步骤进行：①实验教学中学生要主动搜集并分析有关的信息及资料；②实验教学中学生要把当前学习内容与已有的知识相联系，并对这种联系加以认真思考；③实验教学中学生需要充分地与教师和学习伙伴进行交流、讨论，主动接受教师的指导及伙伴的协作完成一首乐曲的音乐合成；④对各种方式得到的结果(乐曲)进行优化(乐音的修饰)并进行验证(对照正式演奏音乐)；⑤最后提交实验报告对自己所做的综合性、设计性实验进行总结。下面是取自学生自己模拟的钢琴音的实验。

步骤1：将钢琴do、re、mi、fa四个音用wavread语句读出并直接画出图像(见图2)。

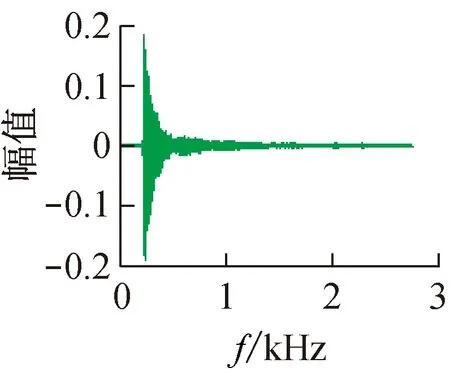
图2 频谱图

步骤2：用曲线拟合法获得钢琴发出声音的包络。

步骤3：使用Matlab中提供的傅里叶级数变换的工具作出钢琴发出音do的频谱图(见图3)。

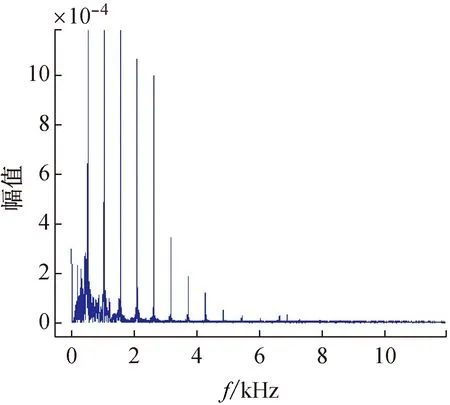
图3 频谱图

步骤4：由傅里叶级数变换频谱图获得钢琴发音的谐波(正弦波的叠加)，频谱图获得的数据见表1。

表1 频谱数据

步骤5：用wavplay语句在Matlab中播放。最后作出由傅里叶级数合成声音的数字信号图像(见图4)。

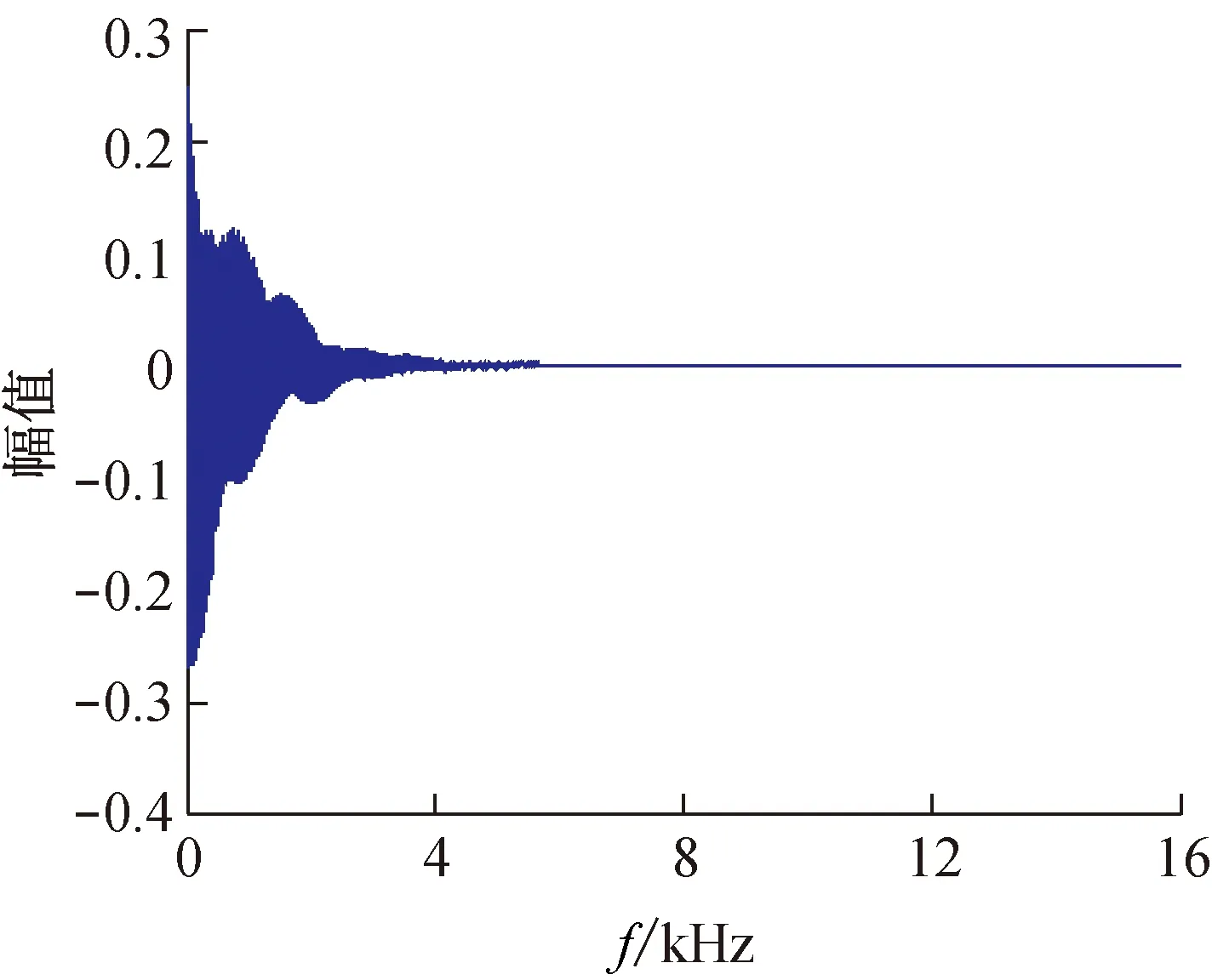
图4 频谱图

有的学生在完成的小提琴、中提琴、大提琴各种音的模拟实验后，以音乐合成[13]了提琴四重奏“情深意长”[14]，许多的学生还用音乐合成了中外名曲。

事实上，培养学生创新能力，对承担实验教学的教师提出了很高的要求。教师作用主要体现在：①组织整个实验教学，从教学内容、教学方法、教学结构等方面作出科学的安排；②激发学生的学习兴趣，帮助学生形成强烈的学习动机；③对学生的学习进行指导，提供掌握整个实验教学的知识架构与学习线索，帮助学生建构所学知识；④对实验教学中的重点、难点进行辅导，帮助学生克服学习难点；⑤创设问题情境，激发学生积极思维，加深学生对所学内容的理解，积极促进知识迁移；⑥培养学生积极的态度、情感，促进个性优良品质的发展；⑦强化教学的创造性，归纳演绎并重，鼓励学生进行求异思维、发散思维，重点培养学生的创新思维能力；⑧在促进学生“学会知识技能”的基础上，着力培养学生“学会学习”。教会学生学习应是实验教学高层次的任务。

5 结 语

“音乐与数学有关吗？”这一讲，在学生中起了轰动性效应，每次课听讲人数达200人以上，在2013年8月西安举办的全国数学建模研讨和经验交流会上发言[15]，获得了与会者一致的好评。这对在综合性、设计性实验中培养学生的创新能力，全面提高大学生的综合素质，推动和深化大学数学教学改革、推动数学建模的活动的开展，无疑是十分有益的。

[1] 易昆南.在综合性、设计性实验中培养学生的创新能力，实验技术与管理[J].2007(8):8-9,14.

YI Kun-nan,Cultivate the students’ innovation ability in the comprehensive design experiments[J].Experiment Technology and Management,2007(8): 8-9,14.

[2] 冯 毅.音乐的革命，从电子音乐到数字音乐[J].艺术评论，2008(10):70-74.

FENG Yi. Music revolution, From the electronic music to digital music[J].Art Criticism,2008(10):70-74.

[3] 浦景东.《月光曲》教学重点的确定和难点突破[J]. 教师之友,1998(2):20-23.

PU Jing-dong. The determination of “Clair DE Lune” teaching emphasis and difficulties[J]. Friends of the Teacher,1998(2):20-23.

[4] 平利川. 频域分辨率和时域包络周期性对音乐音高分辨的影响[J]. 声学学报，2012(3):325-329.

PING Li-chuan. Frequency resolution and time domain envelope periodic impact on music pitch resolution[J]. Acta Acustica,2012(3): 325-329.

[5] 李尚志.数学实验[M].北京：高等教育出版社，2000.

[6] 陈金坤.高保真音响效果的技术评价[J]. 音响技术，2004(6):69-70.

CHEN Jin-kun. High fidelity acoustics technology evaluation[J].Audio Technology,2004(6): 69-70.

[7] 周虹辰. 基于谐波的乐纹提取和音乐检索[J].计算机工程与应用, 2012,48(2):139-141.

ZHOU Hong-chen. Lines extraction and music retrieval that based on the harmonic[J]. Computer Engineering and Application, 2012,48(2):139-141.

[8] 韩佩琦.弦乐器泛音的分析及应用[J].石河子大学学报(自然科学版)，2006,24(4):503-506.

HAN Pei-qi.String of harmonic analysis and application[J].Journal of Shihezi University (Natural Acience Edition), 2006,24(4): 503-506.

[9] 郭 元.频谱音乐[J]. 音乐探索四川音乐学院学报,2006(3):57-59.

GUO Yuan.Spectrum of music[J]. Explorations In Music, Journal of Sichuan College of Music,2006(3): 57-59.

[10] (美)布雷斯韦尔(Bracewell,R.N.).傅里叶变换及其应用[M].殷勤业，张建国 译.西安：西安交通大学出版社， 2005.

[11] 丁 康.离散频谱分析校正理论和技术[M].北京:科学出版社，2008.

[12] 苏金明.Matlab实用教程[M].2版.北京:电子工业出版社，2008(2):122-123.

[13] 李 敏.基于Matlab的音乐分析与合成实验设计[J].大连民族学院学报，2010,12(3):269-271.

LI Min. Based on Matlab music analysis and synthesis experiment design[J]. Journal of Dalian Nationalities University, 2010,12(3): 269-271.

[14] 丁芷诺.弦乐四重奏《情深谊长》,http://www.tudou.com/programs/view/xsnwq5ZkLTo/DING Zhi-nuo. String quartet “Deep emotion”, http://www.tudou.com/programs/view/xsnwq5ZkLTo/

[15] 易昆南.中南大学易昆南音乐合成，http://202.117.3.94/sxtjxy/jxtz/article.jsp?articleId=11421，二分会场报告止园饭店长安厅.

YI Kun-nan. Central South University YI Kun-nan’s beyonding music synthesis, http://202.117.3.94/sxtjxy/jxtz/article.jsp?articleId=11421,Half the meeting report check Changan hall garden hotel.

要全面落实本科专业类教学质量国家标准对实践教学的基本要求，加强实践教学管理，提高实验、实习、实践和毕业设计(论文)质量。支持高等职业学校学生参加企业技改、工艺创新等实践活动。组织编写一批优秀实验教材。思想政治理论课所有课程都要加强实践环节。

——摘自《教思政[2012]1号文件》