基于极值分解的同塔多回高压输电线路电磁兼容预测方法
2014-02-08吴文军
吴 文 军
(上海电力学院, 上海 200090)
0 引 言
同塔多回高压输电系统的谐波污染,除了线路交流电的高次谐波外,电磁干扰也是一大成因。因此,任意分布导体散射场的分析与预测,对于同塔多回高压输电系统的设计与布局、电磁环境的研究和谐波干扰的抑制具有重要意义。其中,在任意干扰源散射作用下,复杂导电体近场分布的数值计算方法的研究具有十分关键的作用和意义,因而得到了理论研究和工程技术人员的广泛关注和深入探讨[1-3]。
任意散射源照射下,复杂导电体近场分布的数模计算在系统电磁兼容性的设计和预测方法中常见的方法是将同塔多回高压输电系统中导电体模拟为面元模型,构造模拟面近似导电体表面,在模拟面上建立子域基电流模型,并运用积分方程结合矩量法求解模拟面上的电流和电荷分布[4-6]。面元模型不仅可描述任意形状的导电体,且适用于计算近场和表面量,但计算更为复杂,所以寻求快速、合理的求解方法成为成功实施面元模型解决电磁兼容性预测的关键。
目前,解决同塔多回高压输电系统非线性电磁干扰求解问题的主要途径有:① 频域分析法[7]。求解频域积分-微分方程,利用高斯-牛顿法反演变换得到系统电磁特性的时域解,系统能够快速收敛,但稳定性不高,易发散。② 直接时域法[8-9]。直接在时域求解时域积分、差分方程,利用梯度法可确保系统稳定反演,获得精确的散射模式的数值解,但收敛速度较慢,特别是逼近极小值时更慢。③ 最小二乘估计方法[10]。结合矩量法求解积分方程,求得矩阵形式的解,然后在复频域利用围线积分和柯西定理,把复频域解表示成留数项之和,可直接把时域解表示成复指数项之和。该方法计算精确度高、稳定性好,兼有前两种方法的优点,但计算量较大,影响了实际效果与应用范围。
频域分析法是分析瞬变电磁场问题的经典方法,但在揭示瞬态响应机理方面不如直接时域法[11-12]。直接时域法能够提供瞬态响应随时间推进的演变过程,但不能像最小二乘估算方法那样反映出瞬态响应域目标特征参量间的直接关系[13-14]。在多回高压输电系统复杂电磁环境中,大多数散射的积分方程分析是在频域,微分方程法是在时域,而时域积分方程位于两者之间,极值分解方法通过结合矩量法求解时域积分方程,使其在确保稳定性的同时,通过预测模型结构获得精确解,因而论文基于极值分解法,结合最小二乘估算策略,提出模式综合电磁预测方法,为电磁兼容性预测面元模型的建立提供了有效的求解途径,实现了同塔多回高压输电线路简单高效、切实可行的电磁兼容预测与分析[15]。
1 耦合电磁干扰问题描述
针对同塔多回高压输电系统中普遍存在的非线性耦合电磁干扰,考察N(N>1)维散射向量任意分布情形下的耦合电磁干扰问题,满足:
(1) 对同塔多回高压输电系统中散射源的几何结构不作限制;
(2) 对向量元素的类型不作限制,无需归一化处理;
(3) 对同塔多回高压输电系统中散射源的放置位置不作限制。
根据电气系统的电磁特性,考察电磁散射模型
F(θ,φ)=θ0Fθ(θ,φ)+φ0Fφ(θ,φ)
(1)
式中:θ0、φ0为θ、φ空间球面坐标系中沿角度方向的单位矢量。据式(1),总散射能量为
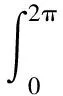
方便起见,定义角球面坐标对(θ,φ)为符号Λ,对应的角度微分为dΛ,则总散射能量可表示为

(2)

(3)
式(3)为最小二乘最优化问题的标准方程形式。定义离散空间中的N维列向量组成矢量p,激励值am组成列向量a,则式(3)可写为
p=Ga
(4)

2 耦合电磁干扰的互耦与极值分解
若式(4)的Gram矩阵中存在互耦,则会令G成为病态矩阵,表明扩展矩阵中的某些向量存在相关性。Gram矩阵中互耦程度的测量依据它的行列式秩数,当
det[(fm,fn)]≅0
由Gram矩阵的直接转置求解式(4)时,可能会因舍入误差导致无解。极值分解技术为此类情况提供了有效的解决途径。
若A为复杂M×N矩阵,则可构造(M+N)×(M+N)矩阵:
式中:W为Hermit矩阵。由构成向量qj做归一化变换,使得
Wqj=σjqj,j=1,2,…,M+N
(5)
式中:σj为特征值。W为对角阵,将qj分解为
式中:uj和vj的分别为M维和N维。式(5)可表示为
Avj=σjuj
(6)
AHuj=σjvj
(7)
式(6)两边左乘AH,结合式(7),可得
(8)
同样,式(7)两边左乘A,结合式(6),可得
(9)

(10)
利用式(10)可生成N×N维矩阵INN,使得:
(11)
(12)
式中:σj为A的极值。所有极值选为正,经归一化变换,可得式(12)的矩阵形式,
A=UHVH
式中:U、V分别为M×M维、N×N维矩阵;H为M×N维矩阵,满足:
式(12)通常称为降阶极值分解形式,可将U、V降为R列,定义UR、VR使得:
(13)
利用式(13),求解最小二乘最优化问题的标准方程式(3),可得:

(14)

由此可向量得解
求取极值实现了散射向量元素与激励参数间的相位转换,从而降低电磁散射效能。
利用模式综合技术,将非线性电磁耦合等效为约束条件,采用最小二乘方法,求解符合应用需求的最优观测值,能够有效抑制能量耦合的影响,确保导电体优良的电磁兼容性能,推导可得求解结果:
(15)
3 实验结果分析
对110 kV同塔四回输电线路采用垂直排列方式,线路模型如图1所示,线路主要参数见表1所示。


参数数量杆塔高度/m58导线型号ACSR⁃720/50导线直径/mm36.2导线直流电阻/(Ω·km-1)0.03984避雷线型号LBGJ⁃150⁃40AC避雷线直径/mm15.75避雷线直流电阻/(Ω·km-1)0.2935避雷线接地方式中性点直接接地
为了验证所设计的电磁抗扰系统的稳定性,基于dSPACE系统, 实时仿真同塔多回高压输电系统电磁场环境,对同塔多回高压输电系统12条线路中近域耦合电磁干扰最为强烈的一条线路进行电磁兼容性能分析,辨识获得的散射向量幅值与相角分别如图2、3中实线所示的幅值轨迹与相角轨迹。利用模式综合预测算法对耦合干扰进行计算与预测,得到了如图2、3中虚线所示的补偿轨线。由波形分析可知:随着干扰源向中心领域的移近,传统最小二乘方法作用下的系统受耦合干扰的影响愈加严重,幅值与相角的最大旁瓣出现了明显的干扰形变,甚至有影响主频域波形的趋势;应用基于极值分解的改进算法,不仅可使干扰作用方向上波形不发生形变,且在主频域内期望轨迹获得快速响应与跟踪,有效补偿了由耦合干扰引起的检测误差,减小了电磁干扰的耦合强度,提高了系统的运行效能。

图2 近域干扰幅值波形对比图

图3 近域干扰相角波形对比图
4 结 语
在分析同塔多回高压输电线路电磁干扰耦合特性的基础上,提出了一种新型的模式综合电磁兼容预测数值分析方法。将极值分解与矩量法相结合,通过适当配置系统的电磁散射方程,精确预测散射干扰的影响,补偿耦合干扰引起的跟踪误差,减少耦合强度,增强系统抗扰能力,能够确保系统稳定运行的同时,实现期望幅值、相角的快速跟随。
由同塔多回高压输电线路中电磁兼容预测方法的设计过程、推导证明和实验测试可得到下列结论:
(1) 存在耦合干扰作用的实际操作环境中,采用模式综合电磁兼容预测算法的同塔多回高压输电线路运行平稳,辨识向量可快速跟踪期望轨迹,克服了传统优化算法中补偿力度不足的缺点,系统稳定性高,鲁棒性强。
(2) 模式综合电磁兼容算法结构简单,运算量小,计算精度高,控制效果好,为分析和设计电磁干扰实时预测方案提供了有效的手段和工具。
(3) 采用模式综合电磁兼容算法的同塔多回高压输电线路具有较好的控制性能和鲁棒特性,算法结构不复杂,实时控制中的计算量也不大,为实现在线实时控制提供了可能。
[1] 孙秋芹,李庆民,吕鑫昌. 同塔多回输电线路并联电抗器的参数优化分析[J]. 中国电机工程学报, 2011,31(25):50-57.
SUN Qiu-qin, LI Qing-min, LV Xin-chang. Parameter optimization analysis of shunt reactor of multi-circuit transmission on the same tower[J]. Proceedings of the CSEE, 2011,31(25):50-57.
[2] 亚哈基,阿比利,沙哈巴蒂,等. 基于大重叠域矩量法的频率选择表面分析[J]. IEEE 微波变电理论与技术, 2010, 58(8):2175-2187.
Yahaghi A, Abiri H, Shahabadi M,etal. Large Overlapping Subdomain Method of Moments for the Analysis of Frequency Selective Surfaces[J]. IEEE Transactions on Microwave Theory and Techniques, 2010, 58(8):2175-2187.
[3] 韩军科,杨靖波,李清华. 超/特高压交流同塔多回输电线路覆冰不平衡张力分析[J]. 电网技术, 2011,35(12):34-37.
HAN Jun-ke, YANG Jing-bo, LI Qing-hua. Analysis on unbalanced tension caused by ice-coating on conductors of UHV/EHV AC multi-circuit transmission lines on the same tower[J]. Power System Technology, 2011,35(12):34-37.
[4] 颜 伟,赵 阳,王恩荣. 复杂电子系统辐射EMI 噪声机理分析与抑制[J]. 中国电机工程学报, 2013,33(15):173-179.
YAN Wei, ZHAO Yang, WANG En-rong. Analysis and suppression of EMI noise mechanism complex electronic systems radiation[J]. Proceedings of the CSEE, 2013,33(15):173-179.
[5] 王玉峰,邹积岩,廖敏夫. 瞬态电磁干扰信号发生器的研制[J]. 高电压技术,2009,35(4):866-871.
WANG Yu-Feng, ZOU Ji-yan, LIAO Min-fu. Development of transient electromagnetic interference signal generator[J]. High Voltage Engineering, 2009,35(4):866-871.
[6] 凯伯勒. 未来智能电网的网格化电能质量和电磁兼容性[J]. IEEE电磁兼容杂志, 2012(1):100-103.
Keebler P F. Meshing power quality and electromagnetic compatibility for tomorrow’s smart grid[J]. Electromagnetic Compatibility Magazine, IEEE, 2012(1):100-103.
[7] Fujii K, Harada S, Sugiura A. An estimation method for the free-space antenna factor of VHF EMI antennas[J]. IEEE Transactions on Electromagnetic Compatibility, 2005, 47(3): 627-634.
[8] 张向明,赵治华,郭 飞. 电磁兼容测试系统电磁干扰问题分析与解决[J]. 电工技术学报,2010,25(10):14-17.
ZHANG Xiang-ming, ZHAO Zhi-hua, GUO Fei. Analysis and resolution of electromagnetic interference in emc test system[J]. Transactions of China Electrotechnical Society, 2010,25(10):14-17.
[9] 易马泽,哈姆卡,刘洪江. 基于直接数据域最小二乘法的中心厄米特形式的两步优化[C]∥IEEE 系统与控制国际会议. 土耳其伊斯坦布尔,2010.
Yilmazer N, Bhumkar S, Hongjiang Liu. A two-step optimization of the centro-hermitian form in direct data domain least squares approach[C]. IEEE International Conference on Systems Man and Cybernetics. Istanbul, Turkey.2010.
[10] 马 超,贾云峰. 基于正交试验设计的系统级电磁自我兼容性的检测方法[C]. IEEE第4次国际研讨会议. 中国北京, 2011.
Chao Ma, Yunfeng Jia. The method of system-level electromagnetic self-compatibility inspection based on orthogonal experimental design[C]. 2011 IEEE 4th International Symposium. Beijing, China.
[11] 薛 花,王育飞. 复杂环境电磁干扰的解耦控制方法研究[J]. 电机与控制学报, 2013,17(7):76-60.
XUE Hua, WANG Yu-fei. Decoupling control method of electromagnetic interference in complex environment[J]. Electric Machines and Control, 2013,17(7):76-60.
[12] 于振伟,杰森米克斯. 基于近场耦合扫描特性化和IC远场辐射的一种改进偶极矩模型[J]. IEEE 电磁兼容变电, 2013,55(1): 97 - 108.
Zhenwei Yu, Jason A Mix. An Improved Dipole-Moment Model Based on Near-Field Scanning for Characterizing Near-Field Coupling and Far-Field Radiation From an IC[J]. IEEE Transactions on Electromagnetic Compatibility,2013,55(1): 97 - 108.
[13] 里佐利,科斯坦佐,蒙塔纳里. 远场性自激振荡微带天线的耦合电磁/非线性优化[C]∥微波研讨会摘要, 美国西雅图,华盛顿州,2002: 123-126.
Rizzoli V,Costanzo A,Montanari E. Coupled electromagnetic/nonlinear optimization of self-oscillating microstrip antennas with far-field performance specifications[C]∥Microwave Symposium Digest, Seattle, WA, USA,2002: 123-126.
[14] 覃宇建,吴 超,何建国. 航天器电磁兼容预测系统设计与实现[J]. 系统仿真学报, 2008,20(18):4859-4861.
TAN Yu-jian, WU Chao, HE Jian-guo. Design and realization of spacecraft electromagnetic compatibility prediction system[J]. Journal of System Simulation, 2011,35(12):34-37.
[15] 李 勃,黄大庆. 一种基于预测法的电磁兼容设计方法研究[J]. 仪器仪表学报,2006,27(6):2499-2500.
LI Bo, HUANG Da-qing. Research of an EMC design methodology based on prediction method[J]. Chinese Journal of Scientific Instrument, 2006,27(6):2499-2500.
