SWAN模式对陆架浅水区有效波高的模拟研究及改进
2014-02-08蒋廷松任建莉沈彩琴
蒋廷松,任建莉,沈彩琴
SWAN模式对陆架浅水区有效波高的模拟研究及改进
蒋廷松,任建莉,沈彩琴
(浙江工业大学机械工程学院能源与动力工程研究所,浙江杭州310014)
验证了QSCAT/NCEP混合风场,并将其作为SWAN模式的驱动风场。以南黄海海域作为目标区域,对SWAN模式在陆架浅水区有效波高的模拟能力进行了研究。研究表明,默认参数下SWAN模式计算的有效波高较JASON-1卫星高度计数据偏小,最大偏差达0.6 m。通过对SWAN模式中各物理过程的分析,确定模式计算值偏小的原因是白浪耗散过大。采用参数修正法对白浪耗散项进行改进,将SWAN模式计算有效波高的均方根误差降低到0.16 m以下,相关系数提高到0.85以上。选择2002年中具有代表性的4个月对改进后SWAN模式进行验证,结果显示SWAN模式在研究区域具有良好的稳定性和适用性。
SWAN;陆架浅水区;白浪耗散;有效波高
1 引言
SWAN模式是荷兰Delft科技大学的Ris等在WAM模式的基础上发展起来的近岸浅水波浪模式[1]。模式采用作用量谱平衡方程描述风浪的产生及演化过程,除全面考虑了能量输入、耗散和非线性相互作用等源项外,还引入了浅水公式,使得SWAN不仅对各种水深的适应性较好,而且模拟结果更接近真实海浪[2]。
在SWAN模式建立之初,Ris等模拟了Haringvliet、Norderneyer Seegat和Friesche Zeegat水域的波浪场,结果表明SWAN计算结果稳定可靠[3]。此后,Gorman等模拟了潮间带河口浅水区的风浪过程[4],Padilla—Hernandez等模拟了澳大利亚Lake George的波浪场[5],Lin等模拟了美国Chesapeake Bay的波浪场[6],结果都表明在中等风速下SWAN模式能够很好地模拟近岸波浪场。
在我国,SWAN模式也得到了广泛的研究。2004年,徐福敏等计算了海安湾的波浪要素[7],结果表明SWAN模式能很好的模拟中国海域的波浪场。2005年,徐艳清等在东中国海对WWATCH和SWAN进行了比较,发现SWAN的模拟结果更好[8]。2009年,闫涛等利用WAVEWATCH与SWAN嵌套模拟了墨西哥湾飓风迪安的波浪场,结果表明嵌套模拟结果好于单纯使用一种模式的模拟结果[9]。2010年,贾晓等对风输入项的拖拽力系数进行了改进,使SWAN模式可以更好的模拟大风速下的波浪场[2]。2011年,王毅对SWAN模型中的海浪耗散参数化方案进行了改进,有效提高了三天海浪预报的可靠性[10]。
中国北方的海域都属于陆架浅水区,因此研究SWAN模式在陆架浅水区的模拟能力具有重要的意义。本文首先对QSCAT/NCEP风场进行了验证,然后以南黄海海域作为目标区域,研究SWAN模式在陆架浅水区中的模拟能力。对SWAN模式进行改进,提高SWAN模式在陆架浅水区中的模拟精度,并用JASON-1卫星高度计数据对改进后的SWAN模型进行验证。
2 SWAN模式的基本原理
2.1控制方程
SWAN模式采用作用量谱平衡方程[11]。作用量密度N(σ,θ,x,y,t)为能谱密度E(σ,θ,x,y,t)与相对频率σ之比,在直角坐标系下,其控制方程可表示为:
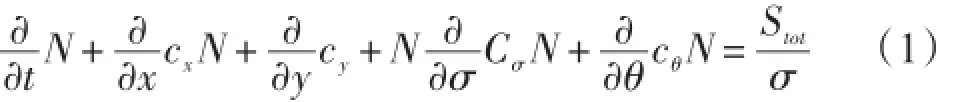
式中,左边第一项表示作用量密度随时间的变化率;第二、三项表示作用量密度在地理空间x、y方向上的传播[12];第四项表示流场和水深引起的作用量密度在σ空间的变化;第五项表示作用量密度在θ空间的传播[13]。方程右边的Stot表示以谱密度表示的源项,其方程为:
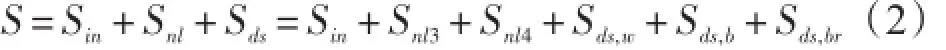
式中,Sin表示风输入项;Snl3和Snl4分别表示三波-波和四波-波相互作用引起的能量变化;Sds,w表示白浪破碎引起的能量耗散,也叫白浪耗散;Sds,b表示底摩擦引起的能量耗散;Sds,br表示深度诱导的波浪破碎引起的能量耗散。
2.2源项处理
2.2.1 风输入项
在SWAN模式中,风输入项可以用共振机制(Phillips,1957)和不稳定机制(Miles,1957)来描述。前者考虑的是波浪随时间的线性增长,后者考虑的是波浪随时间的指数增长。基于这两种波浪增长机制,风生波作用一般可以表示为:
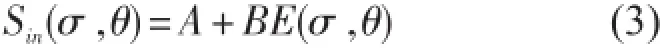
式中,A表示线性增长部分,BE(σ,θ)表示指数增长部分。其中,风指数增长的形式又可以分为Komen(1984)模式和Janssen(1989,1991)模式。
2.2.2 非线性波-波相互作用
在浅水条件下,三波-波相互作用会把能量从低频转移到高频,从而产生高次谐波。在深水条件下,四波-波相互作用将能量从谱峰传向低频,使得谱峰频率降低,同时也将能量传高频,使其通过白浪等耗散,在波谱演化过程中起主要作用。
2.2.3 能量耗散项
SWAN模式中主要考虑了三种类型的耗散机制,包括白浪耗散、底摩擦和深度诱导的波浪破碎引起的能量耗散。在深水情况下,白浪耗散主要控制着谱的高频部分的饱和程度。在中等深度和浅水情况下,底摩擦变得重要。波浪传到浅水破碎带附近时,深度诱导的波浪破碎引起的能量耗散占主要地位。
3 验证资料
采用由ECMWF气象模型插值得到的风矢量数据作为SWAN模式驱动风场的验证数据(下称ECMWF风矢量数据),该数据存放在JASON-1卫星的GDR数据包中,用于卫星数据的校验。采用JASON-1卫星高度计数据中的有效波高数据作为SWAN计算结果的验证数据。发射于2001年的JASON-1卫星是TOPEX/Poseidon的后继卫星,主要用于海平面高度和有效波高的测量,卫星高度计在远海海面高度的测量精度达2—3cm,其高精度的观测资料已经广泛地应用在多个学科领域,取得了令人满意的成果[14]。
JASON-1卫星基本信息如表1[15]所示,卫星的重访周期为9.9156 d,每个周期包含127条轨道,每条轨道分为两条pass进行存储,奇数号pass为升轨,偶数号pass为降轨[16]。高度计每隔0.98 s采样一次,相邻两采样点的间距约为6.8 km[17]。
根据JASON-1卫星通过赤道时的经度表,推算出经过研究区域的pass共有6条,选择cycle001中的pass 138(见图1)和pass 229(见图2)上的数据作为本文验证资料。其中,pass138的测量时间为2002年1月20日13时32分—1月20日14时28分,pass229的测量时间为2002年1月24日02时47分—1月24日03时44分。

表1 JASON-1卫星基本信息
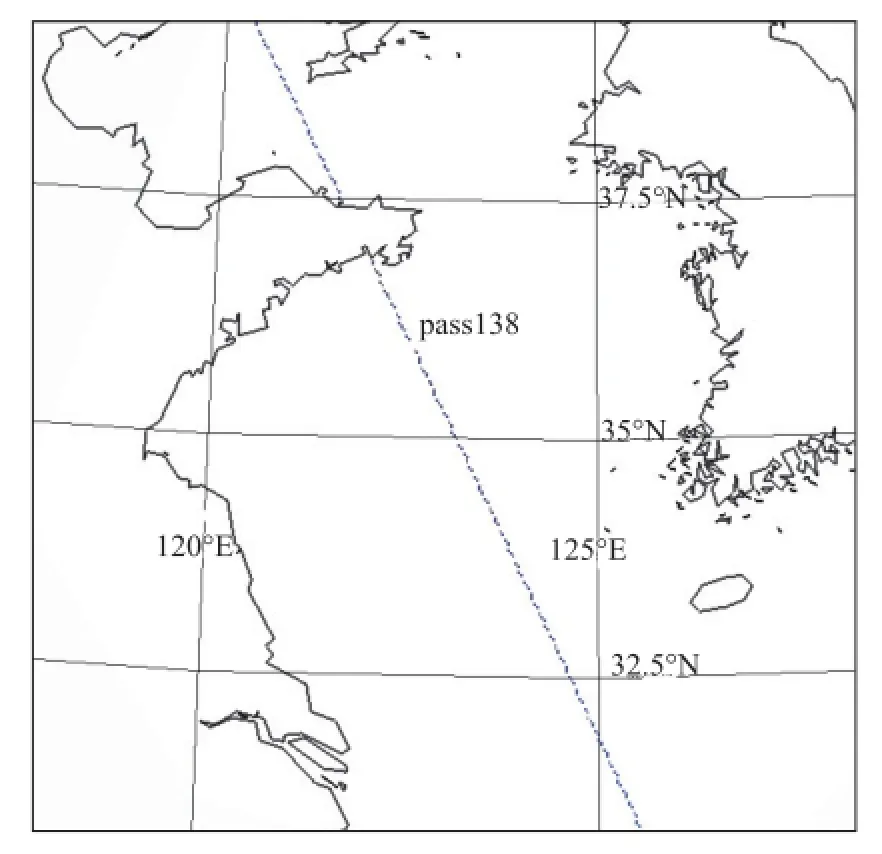
图1 pass 138穿过计算区域的示意图
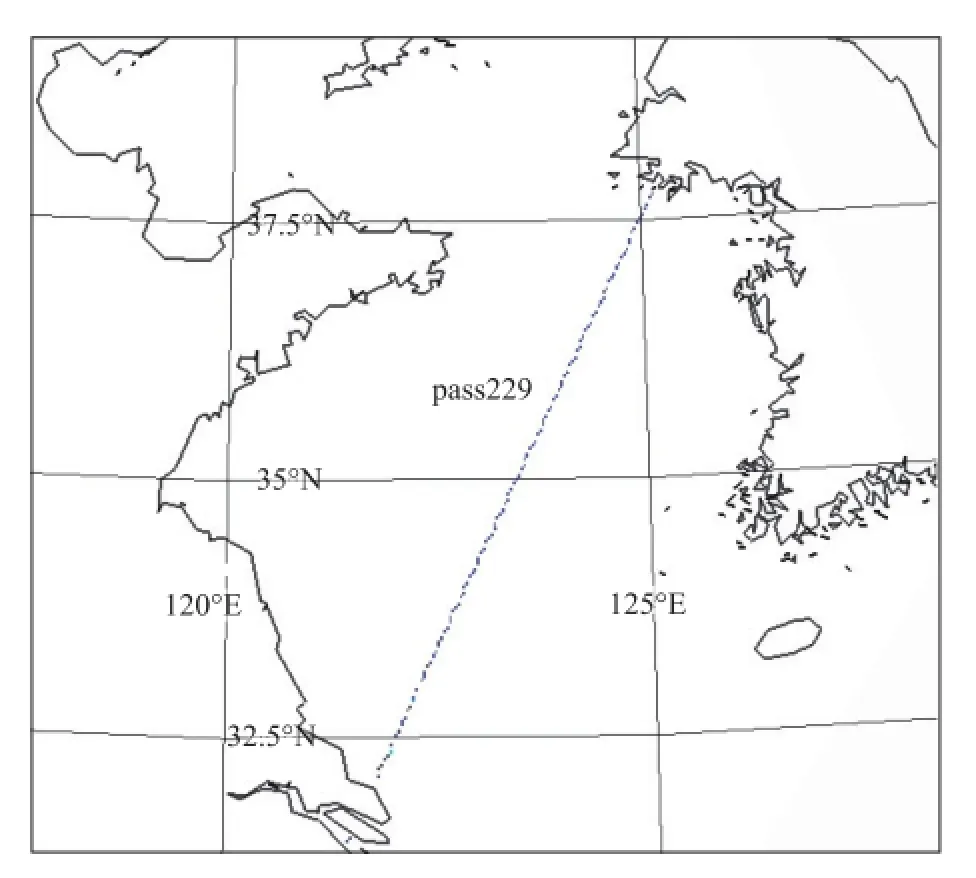
图2 pass 229穿过计算区域的示意图
4 SWAN模式设置
4.1研究海域
如图3所示,研究海域位于南黄海,计算范围为31°—37°N,119°—125°E。南黄海地形规则,海底平缓,平均水深45.3 m,最大水深140 m,属于典型的陆架浅水区,是进行SWAN模拟试验的理想海域。
4.2输入数据
水深地形数据采用ETOPO1数据,分辨率为1′× 1′。驱动风场采用QSCAT/NCEP混合风场,其时间分辨率为6 h,空间分辨率为30′×30′,用线性插值法在空间上插值后的分辨率为5′×5′。王道龙[18]、李靖[19]等人在用ETOPO系列数据和QSCAT/NCEP数据作为SWAN模式输入数据时,均取得了理想的效果。
4.3风场数据验证
用ECMWF风矢量数据对插值后的QSCAT/ NCEP风场进行验证,结果如图4、5。从总体上看,两组数据的趋势基本一致,QSCAT/NCEP风速的u向风较JASON-1风速偏小,v向风较ECMWF风速偏大。pass138上QSCAT/NCEP的u向风较JASON-1偏小,偏差约为1m/s;v向风总体偏大,只在125°—126°E区间内的风速略小于ECMWF风速。pass229上QSCAT/NCEP的u向风总体偏小,在124.3°—125.2°E区间内的风速较ECMWF风速略大;v向风在中间区段(122°—124.7°E)的偏大,两边的风速较ECMWF风速偏小。
用统计方法对QSCAT/NCEP风速和ECMWF风速进行分析,其中,xi代表QSCAT/NCEP风速,yi代表ECMWF风速,x¯和y¯分别表示QSCAT/NCEP风速和ECMWF风速的平均值,N为样本总数,统计量计算公式如下:
均方根误差:
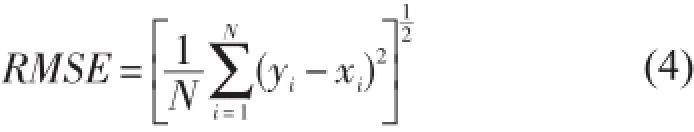

表2 QSCAT/NCEP风速与ECMWF风速的统计分析
相关系数:
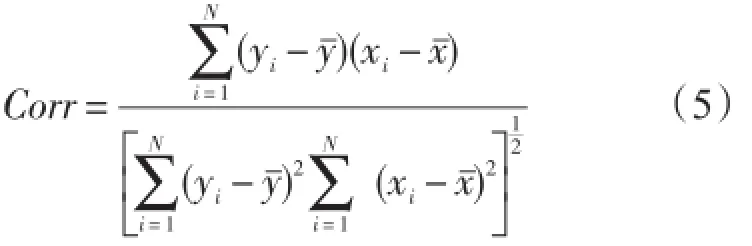
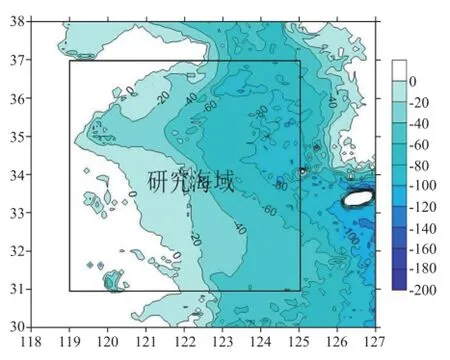
图3 研究海域示意图(水深:m)
从表2中可知,QSCAT/NCEP风速与ECMWF风速的均方根误差在1.62 m/s以下,两者相关系数都在0.9以上,说明QSCAT/NCEP风速与ECMWF风速符合较好。考虑到对比时间存在一定的误差,以及风向不稳定性的影响,结合上述分析可知,QSCAT/NCEP风场基本能够代表研究区域实际的海洋表面风场,可以作为SWAN模式的驱动风场。
4.4数值格式及源项设置
SWAN计算采用二维非稳态模式,坐标系为球面经纬度坐标系,计算网格采用5′×5′的直角网格,时间步长为1 h,计算结果输出数据为有效波高。对主要物理过程设置如下,其他源项采用SWAN默认设置,其中各物理过程的参数均为默认参数:
(1)风输入:采用KOMEN模式;
(2)白浪耗散:采用KOMEN模式;
(3)底摩擦:采用JONSWAP模式,参数采用恒定参数;
(4)开启深度诱导波浪破碎项、关闭衍射项。

图4 ECMWF风速与QSCAT/NCEP风速在pass138上的比较
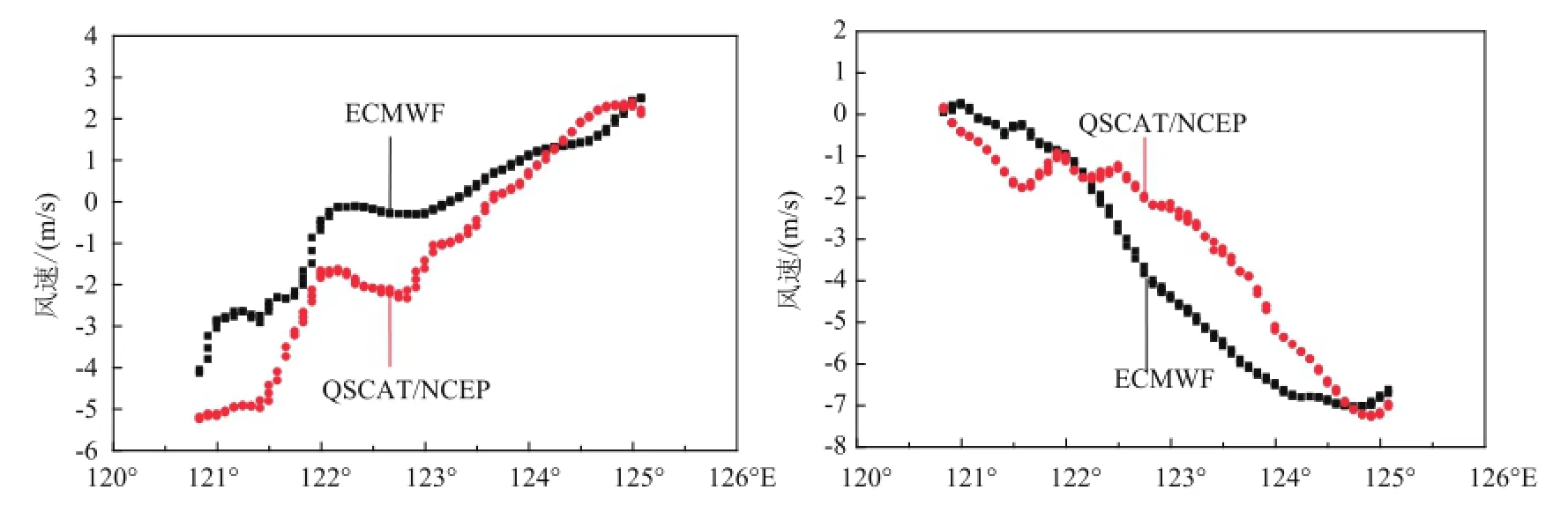
图5 ECMWF风速与QSCAT/NCEP风速在pass229上的比较
初始条件的设置采用SWAN模式中的热启动方法,用2001年12月的计算结果作为模拟试验的初始值。计算的假想边界为30°—38°N,118°—127°E,与实际研究区域的位置关系如图3所示。经与JASON-1数据对比,发现在所选的初始条件和边界条件下,初始值和边界外的涌浪对研究区域的计算结果几乎没有影响。
4.5计算结果
将SWAN计算所得的有效波高与JASON-1卫星高度计数据比较。图6为2002年1月20日14时的计算结果与卫星高度计数据在pass138上的比较,图7为2002年1月24日03时的计算结果与卫星高度计数据在pass229上的比较。
总体上看,SWAN模式计算结果与JASON-1测得的有效波高的变化趋势基本一致,但是模式计算值明显偏小。两条pass上的最大偏差都在125°E附近,偏差值约为0.6m。图6中,在124°E之后,随着经度的增加,水逐渐变深,模式计算结果与高度计数据的偏差逐渐变大。
利用公式(4)和公式(5)对两组数据进行统计分析,式中,xi代表SWAN计算的有效波高,yi代表JASON-1测得的有效波高,x¯代表SWAN计算有效波高的平均值,y¯代表JASON-1测得有效波高的平均值,N为样本总数,分析结果如表3所示。

表3 默认参数下SWAN模式计算的有效波高与JASON-1数据的统计分析
两组数据的均方根误差为0.29m和0.33m,说明默认参数下的SWAN模式在总体上能够模拟出研究区域的波浪场,但是精度不高,而且线性相关度较差,仅为0.833和0.787。综合考虑高度计测量时间与模式计算时间的误差,以及高度计测量造成的位置误差,可以看出默认参数下的SWAN模式能够模拟研究区域的波浪场,但是模拟精度还有待提高。
5 SWAN模式的改进
根据第3节的研究可知,默认参数下SWAN模式在陆架浅水区模拟的主要问题是计算的有效波高偏小。在以往的研究中发现[10,20],SWAN计算结果偏小的原因一般有两点:一是输入风场过小,二是耗散过大。对于第一点原因,3.2.2节中已经对使用的QSCAT/NCEP风场进行了验证,表明其可以用作SWAN模式的驱动风场,因此,造成研究区域计算波高偏小的原因是耗散过大。
SWAN模式中的耗散项包括白浪耗散、底摩擦和深度诱导波浪破碎,其中底摩擦和深度诱导波浪破碎的研究已经比较成熟,通常将白浪耗散作为最不确定的耗散项加以调整[21]。为提高模式在研究区域中的模拟能力,本文通过一系列的数值试验,对的白浪耗散项进行改进。
波浪数值计算中的白浪耗散项描述了深水波浪破碎导致的能量损失,SWAN模型中使用白浪耗散表达式为
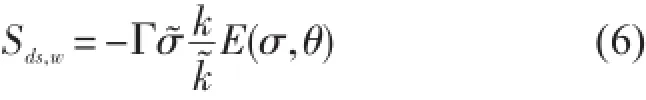
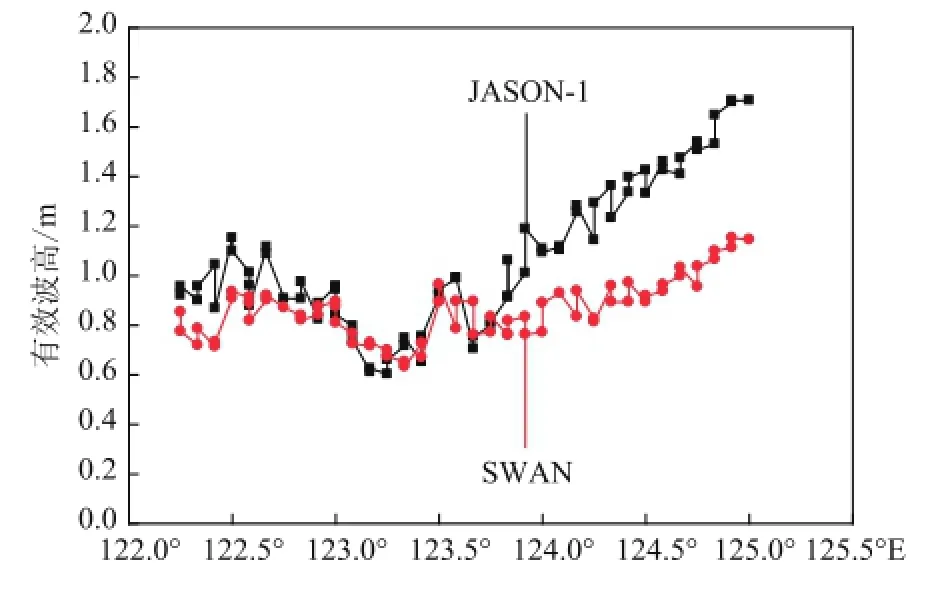
图6 计算波高与pass138上高度计数据比较
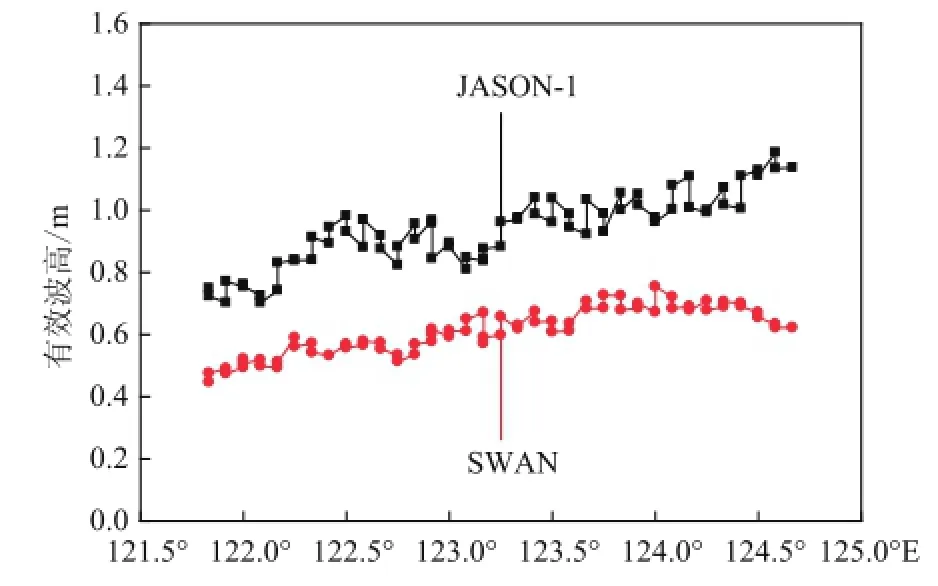
图7 计算波高与Pass229上高度计数据比较
本文中的白浪耗散表达式采用SWAN中默认的KOMEN表达式,对应的风输入方程为KOMEN模式。此时波陡依赖系数Γ的表达式为
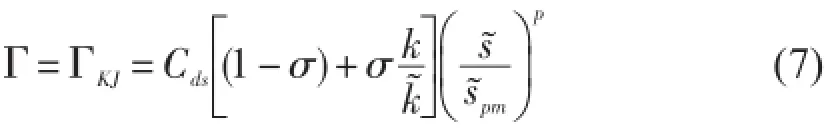
式中,Cds、σ和p均为可调参数,Γ与风输入表达式相关。当对应的风输入方程为KOMEN模式时,默认参数为Cds=2.36×10-5,σ=0,p=4,在实际研究中,用户可根据具体情况对这些参数进行调整。
在计算海浪频率谱的时候,SWAN模式采用了固定的高频截断的方式计算海浪谱的高频部分,Banner和Young(1994)研究发现如果采用KOMEN方案直接计算海浪谱,就会出现海浪谱的高频高估和低频低估现象[10]。王毅在研究中发现,当驱动风场在中、低风速情况下,KOMEN耗散模式中存在明显的高频高估现象,导致耗散过大,从而使得计算出的有效波高明显偏小[10],此结论与本文第3节中的模拟结果一致。在不改变SWAN模式原计算方程的前提下,可以通过修改耗散表达式中可调参数,来抵消由于高频高估造成的耗散过大。从方程(1)、(2)、(6)、(7)可知,系数Cds与白浪耗散呈线性关系,因此通过减小系数Cds,即可增大计算得到的有效波高。
本文共做了10组数值模拟试验,Cds取值从1.06×10-5到1.96×10-5,取值间隔为0.1×10-5。试验中计算有效波高随着系数Cds的减小单调递减,当Cds=1.36×10-5时,计算值与JASON-1数据最为接近,故取该值作为SWAN模式在研究区域中的白浪耗散系数。

表4 改进后SWAN模式计算的有效波高与JASON-1数据的统计分析
图8、图9给出了改进前后SWAN模式计算的有效波高与JASON-1数据的对比图,从图中可以看出,改进后的计算精度明显优于改进前。从表4中可以看出,经参数修改后,模式计算的有效波高与高度计数据的均方根误差减小了接近一半,相关系数提高至0.923和0.902,表明修改参数后,模式在研究海域的模拟能力大大提高。
6 改进后SWAN模式的验证
为了检验改进后SWAN模式在研究海域的适用性,本文选取了2002年的2月、5月、8月、11月四个月份来进行验证。验证地点仍为试验区域,地形因素不变,影响SWAN模式适用性的仅为风场因素。南黄海海域冬季盛行北风,4、5月为季风交替季节,6至8月盛行南到东南风[16],因此所选的验证时间能很好的代表计算区域在一年中的风场特征。
用JASON-1卫星高度计pass229上的数据对改进后SWAN模式计算的有效波高进行验证,验证时间为2002年2月、5月、8月和11月,对应的JASON-1卫星的周期为cycle004、cycle013、cycle023和cycle032,对比结果如图10所示,表5给出了相应的样本统计分析。通过比较可以看出,在全年中,SWAN模式的计算值与实测值相符度良好,相关系数都达到了90%左右,除8月之外,均方根误差均在0.15 m以下。8月份之所以误差较高,是由于波高基数较大,最大波高接近4 m,因此均方根误差较大是合理的。

表5 修改参数后SWAN模式计算的有效波高与JASON-1测得数据的统计分析
验证表明,通过对白浪耗散参数的修正,SWAN模式在南黄海海域有效波高的计算精度显著提高,且模式运行稳定,达到了预期的效果。在其他浅水陆架区,由于地形及风场环境的不同,需要修改的参数值也不同,应采用数值试验法,选择最佳的白浪耗散参数。
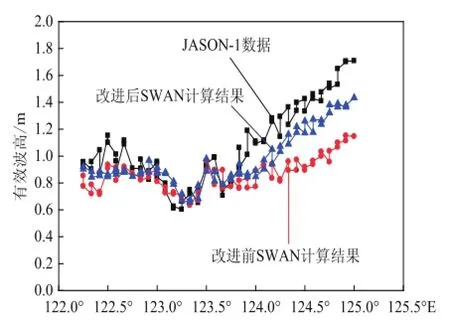
图8 改进前后SWAN与pass138数据比较
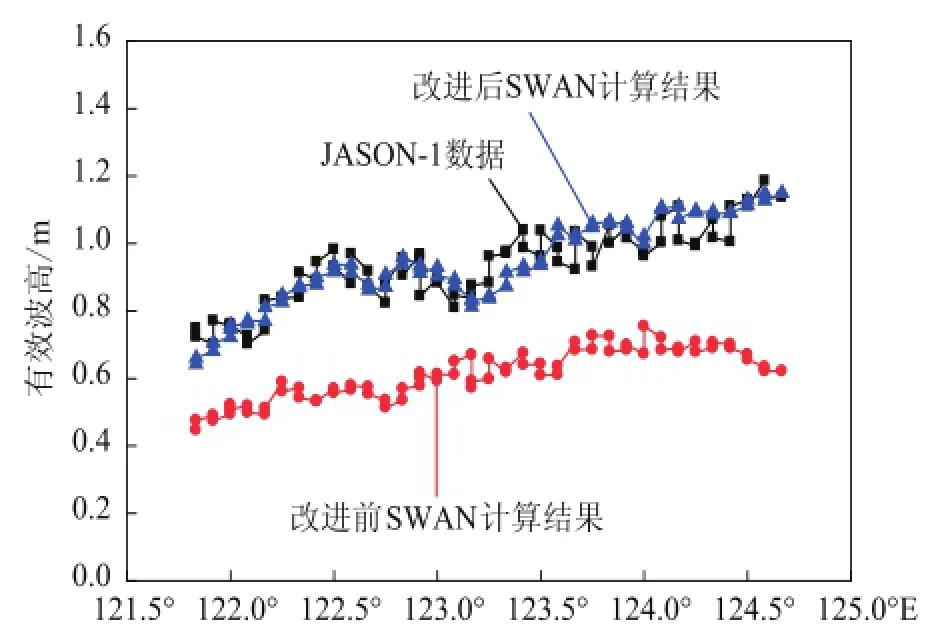
图9 改进前后SWAN与pass229数据比较
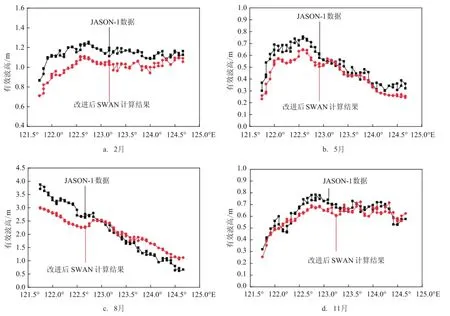
图10 改进后SWAN计算值高与JASON-1数据比较图
7 结论
本文利用验证后的QSCAT/NCEP风场驱动SWAN模式,对南黄海海域的有效波高进行了一系列的模拟研究,并对SWAN模式进行了改进,得到以下结论:
(1)用ECMWF风矢量数据对线性插值后的QSCAT/NCEP风场进行了验证,发现QSCAT/NCEP风场可以作为SWAN模式的驱动风场;
(2)利用默认参数设置下的SWAN模式对南黄海海域2002年1月的波浪场进行了模拟,发现模拟结果与JASON-1实测数据的均方根误差最大达到0.33 m,最低相关系数仅为0.787;
(3)发现在中低风速情况下,SWAN计算的有效波高偏小,在分析了白浪耗散项的数学模型的基础上,采用一种相对简单的参数修正法对白浪耗项进行了改进,并做了一系列数值试验,将模式计算结果与卫星高度计数据的均方根误差减小一半以上,相关系数提高到0.9以上;
(4)用JASON-1数据对改进后的SWAN进行验证,结果表明本文对白浪耗散项参数的修正合理,改进后模式在南黄海海域具有很好的适用性。
[1]Swan Team.Swan user(40.85A)[R].Delft:Delft University of Technology,2008.
[2]贾晓,Bardur N,潘军宁,等.SWAN模型风能输入项的改进与验证[J].河海大学学报(自然科学版),2010,38(5):585-591.
[3]Ris R C,Holthuijsen L H,Booij N.A third-generation wave model for coastal regions 2.Verification[J].Journal of Geophysical Research,1999,104(4):7667-7681.
[4]Gorman R M,Neilson C G.Modeling shallow water wave generation and transformation in an intertidal estuary[J].Coastal Engineering,1999,36(3):197-217.
[5]Padilla H R,Monbaliu J.Energy balance of wind waves as a functionofthebottomfrictionformulation[J].Coastal Engineering,200l,43(2):131-148.
[6]Lin W Q,Sanford L P,Suttles S E.Wave measurement and modeling in Chesapeake Bay[J].Continental Shelf Research,2002, 22(18-19):2673-2686.
[7]徐福敏,张长宽,陶建峰,等.浅水波浪数值模型SWAN的原理及应用综述[J].水科学进展,2004,15(4):538-542.
[8]徐艳清,尹宝树,杨德周,等.东中国海海浪数值模式的研究[J].海洋科学,2005,29(6):42-47.
[9]闫涛,张宇铭,胡保全,等.WAVEWATCH和SWAN嵌套模拟台风浪场的结果分析[J].海洋湖沼通报,2009,4:1-7.
[10]王毅.SWAN模式及数据同化技术在海浪预报中的试验研究和应用[D].青岛:中国海洋大学,2011.
[11]Zubier K M.Numerical wave simulations on different oceanic scales[D].Maine:The University of Maine.2002.
[12]Scientific and technical documentation(40.85)[R].Delft:Delft University of Technology,2008.
[13]李燕,薄兆海.SWAN模式对黄渤海海域浪高的模拟能力试验[J].海洋预报,2005,22(3):75-82.
[14]刘博,甘薇薇,任凤杰,等.Jason-1海洋地形卫星介绍[J].贵州气象,2011,35(1):42-44.
[15]程永存,徐青,刘玉光,等.T/P,Jason-1测量风速及有效波高的验证与比较[J].大地测量与地球动力学,2008,28(6):117-122.
[16]PO.DAAC.AVISO and PODAAC User Handbook[K].IGDR and GDR Jason Products,2004.
[17]于振涛.JASON-1和TOPEX/POSEIDON卫星高度计数据在中国海和西北太平洋的校正、印证及数据融合[D].青岛:中国海洋大学,2006.
[18]王道龙.近岸海浪模式研究[D].青岛:国家海洋局第一海洋研究所,2009.
[19]李靖,周林,郑崇伟,等.台湾海峡及其邻近海域波浪能资源评估[A].中国可再生能源学会.中国可再生能源学会2011年学术年会论文集[C].中国可再生能源学会,2011:4.
[20]张进峰.典型海域的海浪数值模拟研究[D].武汉:武汉理工大学,2005.
[21]Rogers W E,Paul A H,David W W.Investigation of Wave Growth and Decay in the SWAN model:Three Regional-Scale Appljcations[J].J Phys Oceanogr,2003,33:366-389.
[22]Komen G J,Hasselmann S,HasseJmann K.On the existence of a fully developed wind-sea Spectrum[J].J Phys Oceanogr,1984, 14:l27l-l285.
[23]Janssen P A E M.Consequences of the effect of surface gravity waves on the mean air flow[J].Int Union of Theor and AppI Mech(IUTAM),1992,193-198.
Simulation of significant wave height in the shallow shelf area by SWAN model and its improvement
JIANG Ting-song,REN Jian-li,SHEN Cai-qin
(Institute of Energy and Power Engineering,College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou 310014,China)
An assessment of SWAN model in shallow shelf area was performed through the simulation of significant wave height in South Yellow Sea in this paper.The QSCAT/NCEP blended wind field was used to drive the SWAN model.The data of significant wave height calculated by SWAN model with default index were compared with the data extracted from Jason-1 satellite altimeter.Results indicated that the modeled result was smaller than the satellite result,and the maximum deviation was 0.6 meter.By analyzing the main physical process of SWAN model,the reason of data deviation is attributed to higher whitecapping dissipation.The parameters correction method of whitecapping dissipation index was presented,and has been successfully used to improve the SWAN modeling performance in shallow shelf area.The modified simulation result showed that the deviation of significant wave height decreased below 0.16 meters,and the correlation coefficient increased to more than 0.85.Finally,the modified SWAN model was used to calculate the significant wave height for four typical months in 2002.It was found that the simulation results from modified SWAN model were compatible with Jason-1 data.The modified SWAN model is suitable and stable for simulation of significant wave height in Shallow shelf area.
SWAN;shallow shelf;whitecapping dissipation;significant wave height
731.22
A
1003-0239(2014)04-0009-09
10.11737/j.issn.1003-0239.2014.04.002
2013-07-25
蒋廷松(1988-),男,硕士研究生,主要从事波浪能资源分析。E-mail:3notgiven@sina.com
