综合时间序列与高程的天顶对流层延迟模型研究

周淼 ，刘立龙，张腾旭，张朋飞，黄良珂

(1.桂林理工大学测绘地理信息学院，广西桂林 541004;2.广西空间信息与测绘重点实验室，广西桂林 541004)

1 引言

随着卫星定位技术的迅猛发展，在实际应用中对定位精度的要求越来越高，而对流层延迟是定位精度影响的。削弱对流层影响的方法主要有参数估计法、模型改正法等［1］。其中在模型改正法中，传统的对流层改正模型 Hopfield［2］及 Saanstamonien［3］能对流层延迟误差，但在区域对流层延迟改正中精度不能满足需求。为此许多国内外学者提出建立区域对流层模型来消弱对流层延迟的影响，其可行性和有效性都得到了广泛证明［4～6］。文献［1］、［4］分别利用广西地区区域CORS网实测数据和香港CORS网数据建立了广西地区及香港地区的精密天顶对流层延迟新模型，其精度与一般模型精度相比更优。

本文采用加州福利亚地区26个IGS站近4年(2008年～2011年)的天顶对流层延迟数据，通过对傅里叶五阶函数所确定的对流层年周期变化函数和指数函数的加权组合，得到了加州地区区域天顶对流层延迟模型。

2 模型的建立

2.1 数据分析

本文采用加州地区26个永久跟踪站(IGS)4年天顶对流层延迟数据，其采样间隔为 30 s，采用 Bernese GPS Software Version 5.0解算，其精度优于 4 mm。其经度分布为240.48°～243.61°，纬度范围为33.25°～33.93°，高程范围为 －27.56 m ～842.55 m。

为了研究加州地区的ZTD与经纬度及高程之间的关系，分析了4年平均ZTD与经纬度高程三者之间的相关系数，其分别为 －0.377 1、－0.295 8、－0.998 5。从相关系数可以看出，在研究区域的ZTD与纬度存在中等相关，在研究区域的ZTD与经度存在弱相关，而与高程存在强相关。故在接下来的研究中剔除不显著的影响因素，只保留影响因素较大的高程因素。

为研究ZTD与时间序列(即年积日)的关系，选取了高程间隔大致相同的 sio3、csn1、rock、gold、chil等 5个站的4年平均ZTD和研究区域所有站点total 4年的平均ZTD来进行分析。从图1中可知，各站ZTD随年积日的改变而呈曲线变化，且变化趋势相同，故可以利用相关函数拟合，如傅里叶函数、高斯函数或者多项式函数等。

图1 研究区域ZTD与年积日的关系

2.2 与高程相关函数模型的建立

ZTD与高程的关系成负指数相关或线性相关，在结合研究区域实际情况下比较得出两者并没有较大差异，指数拟合稍好于线性拟合［1］。由指数函数拟合对流层得到方程为:ZTD(H)=a·exp(－b·H) (1)经拟合后可解出方程参数，其中a=2.222，b=0.07222。

2.3 与时间序列相关函数模型的建立

将加州地区IGS站点4年日平均ZTD相加取平均值，再分别利用傅里叶函数(F表示，F5表示傅里叶五阶函数，其他类同)、高斯函数(G表示)、多项式函数(P表示)拟合，其RMS如表1所示，拟合图如图2所示:

数据处理前后中误差 表1

图2 平滑前各曲线拟合模型拟合图

由表1可知，在选择初始函数时，各模型的中误差比较接近，改变模型的阶数并不能有效提高模型精度。但在高阶函数中，阶数过高使得两端噪声过高，阶数过低又不能很好反映数据变化规律，从图2上可以看出傅里叶模型、高斯模型和高阶多项式模型中，噪声在数据的开端及末尾波动比较剧烈。在本文中，傅里叶五阶函数在噪声方面比较小，在数据两端波动较平缓，综上，选择傅里叶五阶函数作为时间序列的拟合模型。

2.4 综合时间序列与高程的天顶对流层延迟模型的建立

由以上综合分析知道，与加州地区天顶对流层延迟相关的因素主要为高程及时间序列，因此可以建立起加州地区与高程及时间序列的对流层延迟模型。模型为:

其中，ZTD(D，H)为本文建立的对流层延迟模型，D为年积日，H为高程，ZTD(D)傅里叶五阶拟合函数，ZTD(H)为高程指数拟合函数。

按照经验定权规则，其定权规则为:

式中，△i(i=1，2，…n)为各影响因素的最大值与最小值之差。研究区域中，最低 lbch站的高程为－27.56 m，年均ZTD为 2.380 m，最高monp站的高程为 1 842.55 m，年均 ZTD为 1.900 m，两站之间的ZTD相差为 0.356 m。在各站365天平均取得的ZTD中最大值与最小值之差为 0.123 m，由此可得研究区域的对流层延迟模型为:

各站经拟合后中误差 表2

按式(5)来计算加利福尼亚地区的ZTD得出的值见表2，由表2可以看出，中误差变动幅度较大，成两头大中间小的趋势。具体表现为在站点高程低于100 m时，其中误差都大于 4 cm，其中最大的为azu1站，为 5.6 cm;当高程在 100 m～1 000 m左右时，中误差总体变化比较平稳，且精度比较高;在高程大于1 000 m左右时，其误差波动较大，其中最大误差出现在高程最大的monp站，其中误差为 7.21 cm。显然在高程在 100 m以下、1 000 m以上的区域，其拟合精度有改进空间。经分析，方程(1)的用傅里叶五阶函数拟合加州地区的ZTD，可以反映出ZTD随时间变化的规律，但在数据拟合用的这一区域所有IGS站4年平均对流层延迟，在高程较高和较低的地区没有很好地反映这类地区的ZTD，故可以对高程分段拟合，接下来对加州地区对流层模型加以改正。

改正方法:抽取高程小于 100 m，高程在 100 m～1 000 m之间和高程大于 1 000 m的3个层次分别进行以上步骤进行拟合。其拟合精度如表3所示。

各站改正后中误差 表3

从表3中可以看出，在进行高程分区后，各站点的精度有明显提高，尤其是在高程的两端，其效果更加明显。

3 模型的预报

为了验证模型的实用性，本文用IGS站各站点的2012年的数据进行验证性试验。由于2012年中许多站数据的缺失和不完整性，剔除不满300天数据的站点。其可用站点的天顶对流层延迟中误差如表4所示。

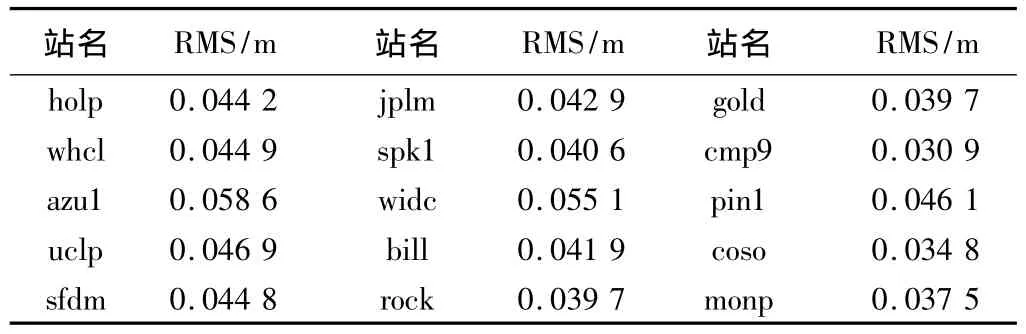
模型预报2012年ZTD中误差 表4

从表中可以看出，在预报2012对流层延迟中，模型的精度在厘米级，其中精度最低的点是azu1站，为5.86 cm;精度最高的点是cmp9站，为 3.09 cm。平均精度为 4.31 cm，因此该模型精度能满足GNSS米级定位精度对流层延迟改正需要。

4 结论

本文建立的天顶对流层模型较为简单，不需要实测气象参数，且需要的参数较少。由于是建立在该地区的模型，具有地域特性，能较好反映当地对流层变化规律。在研究区域，对流层延迟与经纬度没有显著关系，与高程存在较强的相关性。通过拟合比较分析，发现五阶傅里叶函数拟合模型及高程指数拟合模型能较好反映该地区对流层变化。新模型在预报对流层延迟时，其平均精度可达到 4.31 cm，该模型精度可满足GNSS米级定位精度对流层延迟改正需要。本文建立的模型是以每日的天顶对流层数据来建模，因此在小尺度时间上具有一定的局限性。

［1］ 刘立龙，黄良柯，姚朝龙等．基于区域CORS网天顶天顶对流层延迟4D建模研究［J］．大地测量与地球动力学，2012，32(3):45 ～46．

［2］Hopfield H S．Journal of Geophysical Research［J］．1969，74:4487．

［3］Saastamonien J．Contributions to the Theory of Atmospheric Refraction［J］．bulletin Geodesique，1972，105(1):279 ～298．

［4］李薇，袁运斌，欧吉坤等．全球对流层天顶延迟模型IGGtrop的建立与分析［J］．科学通报，2012，57(15):1317～1318．

［5］戴吾蛟，陈招华，匡翠林等．区域精密天顶对流层延迟建模［J］．武汉大学学报·信息科学版，2011，36(4):392 ～393．

［6］卢献健，晏红波，任超．常用天顶对流层区域拟合模型的比较分析［J］．全球定位系统，2010，26～26．

［7］曲伟菁，朱文耀，宋淑丽等．三种天顶对流层延迟改正模型精度评估［J］．天文学报，2008，49(1):113～114．