钢板移动式感应加热过程工艺参数分析与局部变形预测

陈诚，张雪彪，刘玉君，汪骥

1 大连理工大学运载工程与力学学部船舶工程学院，辽宁大连116024

2 大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024

0 引 言

船体曲面外板的水火弯板工艺是一项复杂的工艺技术，在船厂，通常采用氧乙炔火焰作为热源来对钢板进行加热，操作时，需要调整氧气和乙炔气的流量与压力。火焰燃烧因属化学反应，温度难以控制，并且还会释放出CO2气体［1］。而感应热源与火焰热源相比，感应器的功率及其分布较容易控制，可通过调节电磁场的频率来控制钢板加热的渗透深度，精确控制加热温度，加热过程快速、均匀，工件材料氧化少［2］。另外，感应加热系统易与机器人系统进行集成以进行自动化加工［3］。因此，以电磁感应为热源的线加热成形工艺越来越受到人们的重视［4-7］。

对钢板进行感应加热时，感应器首先在钢板表面形成涡流，产生焦耳热，然后在钢板内部进行热传导；钢板的热量吸收是焦耳热和热传导的混合作用，其加热速度快，厚度方向的温度梯度大。由于钢板火焰加热与感应加热的热传输方式不同，导致两者的温度场不同，应力和应变场也不同，这样，钢板的成形规律便由量变发生了质变，因此与火焰热源相比，有新规律需要研究。

从工艺影响参数方面考虑，钢板感应加热的影响参数与火焰加热不同，其主要工艺参数有感应电源功率、感应电源频率、感应器的移动速度及感应器与钢板表面之间的空气间隙等。正交试验设计是用于多因素试验的一种方法，设计的正交表具有“均衡分散，整齐可比”［8］的特点，可以从全面试验中挑选出有代表的点进行试验，常用于试验设计中对主要影响因素的分析和寻找最佳参数组合。本文将首先进行钢板感应加热影响参数的正交试验分析，确定影响钢板温度和变形的主要工艺参数，然后通过数值计算方法探讨主要工艺参数与钢板变形之间的关系，建立钢板变形与主要工艺参数之间的数学模型，通过预测数据与实验数据之间的对比，验证数学模型的正确性。

1 钢板感应加热的正交试验设计

实验室的钢板感应加热设备为高频感应电源设备SPZ-70，对于一定板厚范围的钢板，加热时的频率是一定的，因此，可以控制的加热参数为加热功率、感应器的移动速度和空气间隙。根据实际的试验条件，每个参数选取3 个水平进行比较，所挑选的参数及水平如表1 所示。

依据表1，根据参数的个数和各参数水平的个数，不考虑各参数间的交互作用，选择L9（34）正交表，表头设计如表2 所示。

表1 钢板感应加热试验因素水平表Tab.1 Factors level of steel plate induction heating test

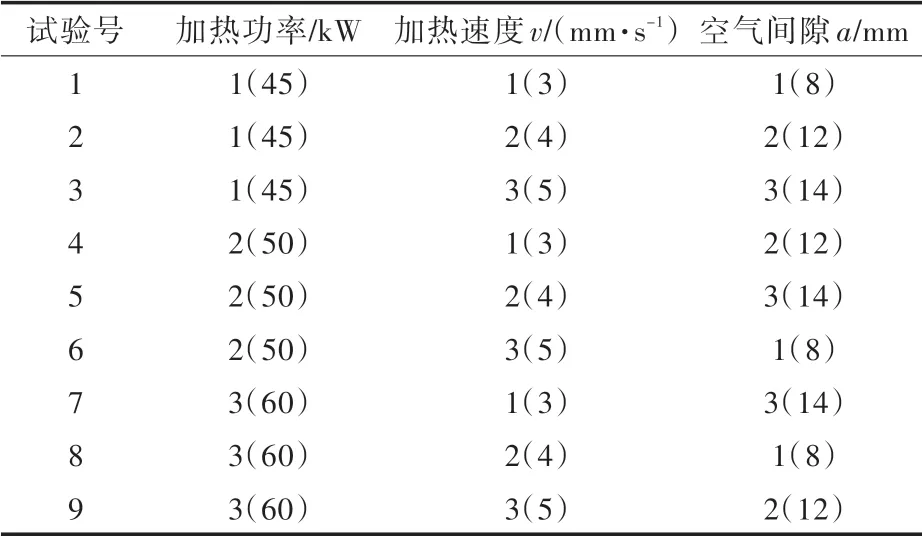
表2 正交试验方案表Tab.2 Orthogonal test design table

试验安排好后，即可按照试验号的顺序安排加热线。在一张试验钢板上依次进行感应加热试验，每条焰道只进行单次感应加热，感应加热试验中的工艺参数如表3 所示。加热时，测量焰道板边处M 点的温度，其横向收缩量是焰道两侧11 对等间距点加热前后的收缩值，如图1 所示。图2 所示为试验现场，图3 所示为感应器移动时钢板的加热状态。这里主要关心的是加热功率、加热速度和空气间隙这3 个参数对钢板加热温度和变形影响的主次顺序，因此，选择板边处焰道末端点M的最高温度和11 对测量点的横向收缩变形量的均值作为考核指标。表4 和表5 分别为温度和变形的正交试验设计计算表。

表3 感应加热的工艺参数Tab.3 The process parameters of induction heating

图1 试验布置图Fig.1 Experimental arrangement

图2 试验和测量现场Fig.2 Experiment and measurement site

图3 感应器移动时的钢板感应加热状态Fig.3 The state of moveable induction heating of plate

表4 正交试验数据分析计算表（温度）Tab.4 Computation of orthogonal test data analysis（temperature）

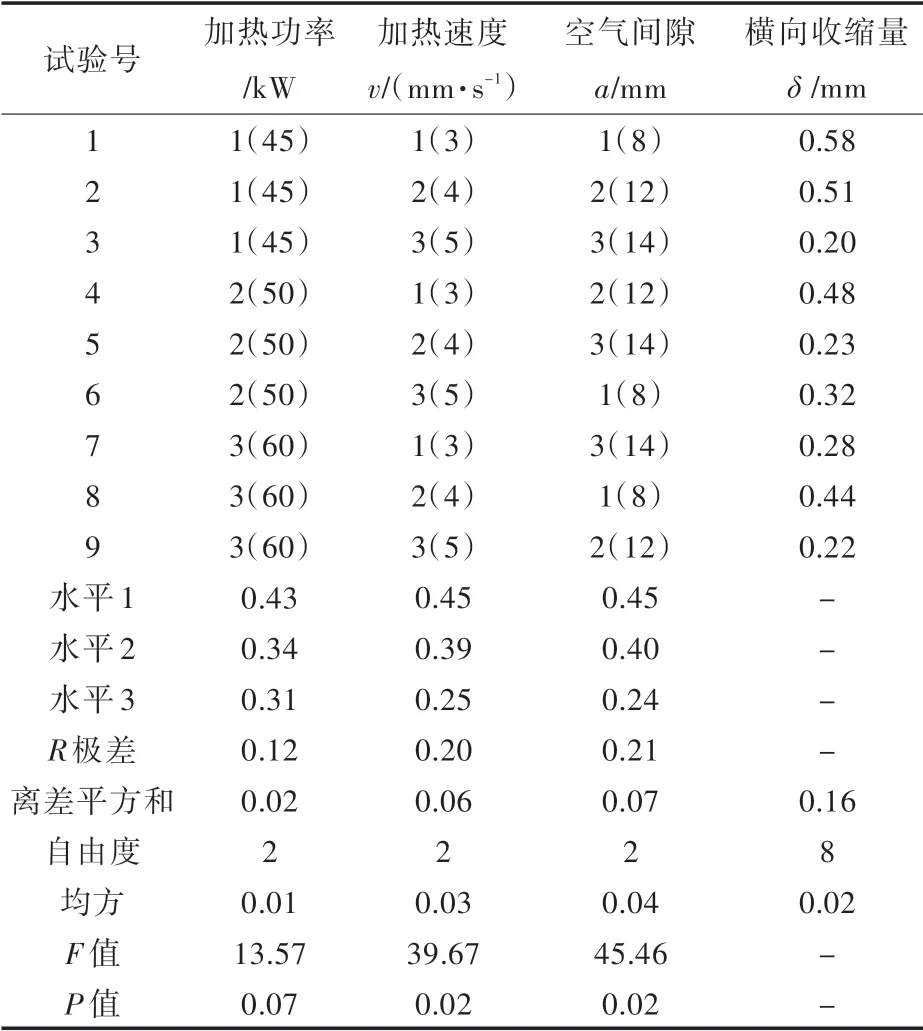
表5 正交试验数据分析计算表（变形）Tab.5 Computation of orthogonal test data analysis（deformation）

表4 中，按照极差大小，工艺参数对温度影响的主次顺序分别为加热速度、空气间隙和加热功率。但是从显著性概率P 值与F 统计值来分析，当显著性概率P 值小于0.05 与F 统计值大于临界值F0.05（2，2）=19 时，认为该参数对试验结果有显著影响，而从表中的计算结果看，3 个参数的P 值均大于0.05，F 统计值均小于临界值19。在一定的空气间隙范围内，感应器与钢板之间会产生强烈的电磁感应，此时，钢板表面的温度主要取决于电磁感应加热的集肤效应，即在一定频率条件下，钢板表面集肤层内的金属温度均会在涡流的作用下快速升温至居里点温度（720 ℃）以上。因此，当空气间隙在感应范围内变化时，钢板表面的温度都会达到居里点温度之上；功率和移动速度的变化对钢板表面的温度不构成决定性的影响。

表5 中，按照极差大小，工艺参数对横向收缩变形影响的主次顺序分别为空气间隙、加热速度和加热功率。从显著性概率P 值与F 统计值来分析，当P 值小于0.05、F 统计值大于临界值F0.05（2，2）=19 时，认为该因素对试验结果有显著影响，而从表中的计算结果看，加热功率的P 值大于0.05，加热速度和空气间隙的P 值则小于0.05；加热速度和空气间隙的F 统计值均大于临界值F0.05（2，2）=19，加热功率的F 值小于19。通过综合极差分析和方差分析结果，发现对于收缩变形而言，加热速度和空气间隙这两个因素是钢板感应加热的主要影响因素，加热功率是次重要影响因素。

2 钢板感应加热工艺参数的数值分析

通过对正交试验设计的工艺参数的分析，发现对于一定厚度的钢板，影响变形的主要工艺参数是加热速度和空气间隙，加热功率属次重要影响参数。由于纵向收缩量和纵向角的变形较小，工艺参数对其影响不大，因此本文将不对其进行重点分析。下面，将通过数值分析方法探讨空气间隙和加热速度这两个工艺参数与横向收缩量、横向角变形和垂向位移Uz之间的关系。

图4 电磁—热—结构耦合计算流程图Fig.4 Flow chart of coupled electromagnetic-thermal-structural calculation

基于ANSYS 软件，模拟钢板移动式感应加热的多物理场耦合过程，图4 所示为电磁—热—结构耦合计算的流程图，计算时的工艺参数同表3。加热方案如表6 所示，其中，空气间隙取3种水平，加热速度取5 种水平，以横向收缩量、横向角变形和垂向位移Uz作为比较的依据。

钢板的屈服应力是随着钢板温度的升高而逐渐减小［9］。本文参考文献［10］，取钢板出现明显塑性变形的临界温度为450 ℃。

表6 钢板感应加热数值设计方案Tab.6 Numerical test conditions of steel plate induction heating

图5～图11 所示为在12 mm 空气间隙、50 kW加热功率的工艺参数条件下，通过改变感应器的速度所得到的温度、变形分析图。其中，图5 所示为钢板在4 mm/s 加热速度条件下，Y=150 mm 截面在感应加热器中心经过截面正上方时厚度方向的温度云图。图6、图7 分别为在4 mm/s 加热速度条件下，钢板加热后的横向收缩量云图和垂向位移云图。图8 所示为在5 种加热速度条件下，Y=150 mm 截面在感应加热器中心经过截面正上方时厚度方向的温度分布图，随着加热速度的提高，截面中高于临界温度的钢板深度（以下统称为“厚度方向的加热深度”）越来越浅。由图9 可见，随着加热速度的提高，钢板横向收缩量逐渐减小。由图10 可看出，钢板横向角变形是随着加热速度的增加而增大，但在v=5 mm/s 后角变形趋于稳定。由图11 可看出，垂向位移值同横向角变形一样，是随着加热速度的提高而增大，但在v=5 mm/s 后垂向位移量趋于稳定。分析图8～图11可知，厚度方向的加热深度增加后，钢板倾向于发生横向收缩变形，对钢板的横向角变形和垂向位移不利。同时由图9 可发现，横向收缩量值在板边处略低，这主要是由电磁感应加热的板边效应导致的，因此对板边效应需做进一步的深入研究。另由图10 可发现，当加热速度v=2 mm/s 时，板边位置处的钢板在厚度方向上被完全加热，出现了反向角变形。

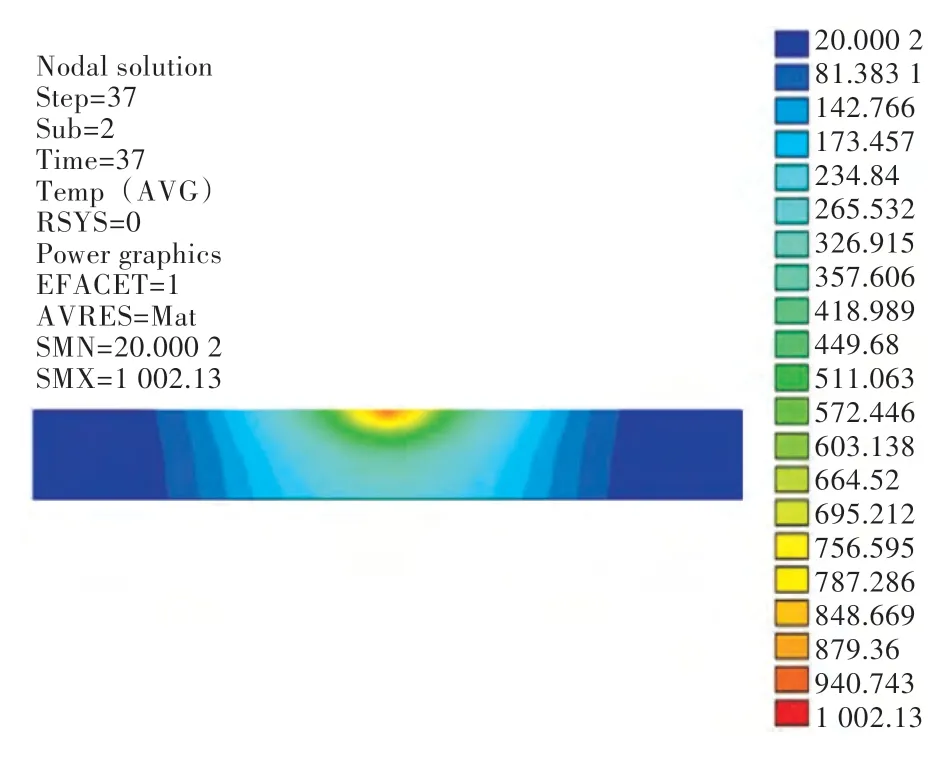
图5 Y=150 mm 截面温度云图（12 mm 空气间隙）Fig.5 Temperature contours of Y=150 mm section（air gap a=12 mm）

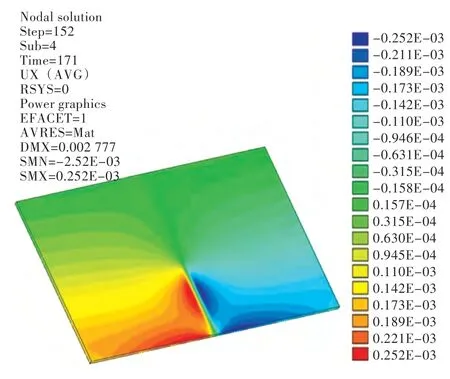
图6 横向收缩云图（12 mm 空气间隙）Fig.6 The contours of transversal shrinkage（air gap a=12 mm）

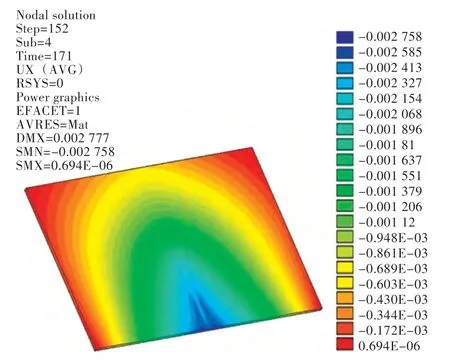
图7 垂向位移云图（12 mm 空气间隙）Fig.7 The contours of vertical displacement（air gap a=12 mm）

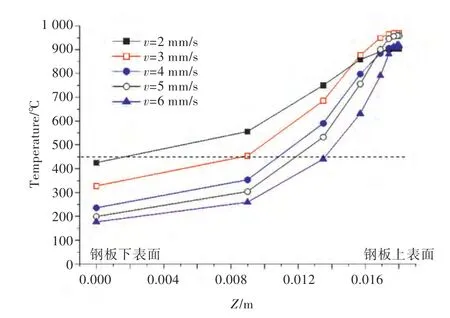
图8 Y=150 mm 截面厚度方向温度分布图（12 mm 空气间隙）Fig.8 The temperature distribution of Y=150 mm section in the thickness direction（air gap a=12 mm）

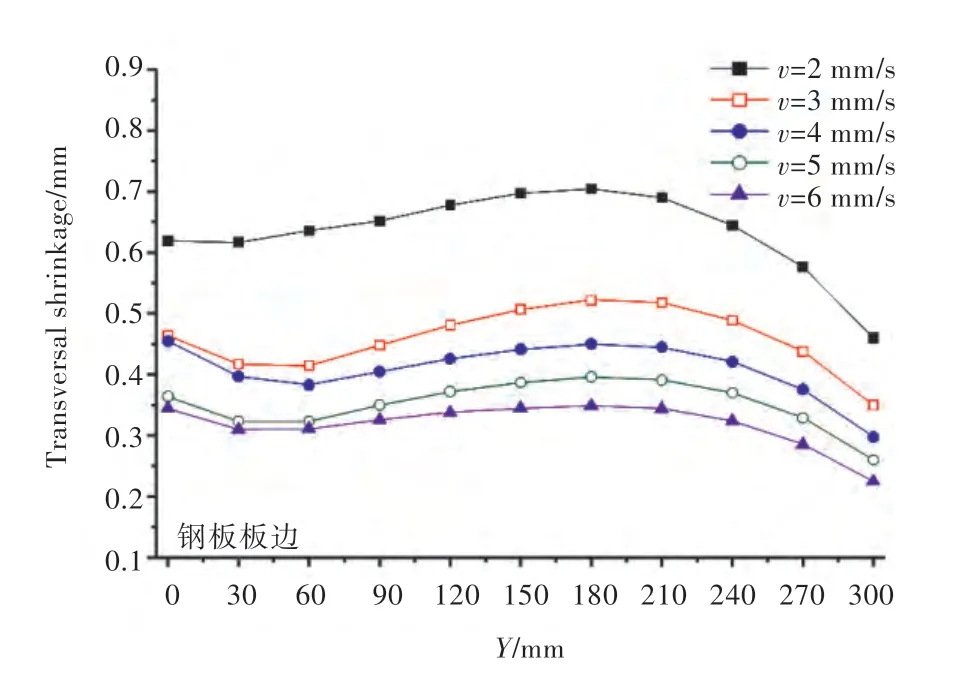
图9 横向收缩量分析图（12 mm 空气间隙）Fig.9 The analysis chart of transversal shrinkage（air gap a=12 mm）

图10 横向角变形分析图（12 mm 空气间隙）Fig.10 The analysis chart of transversal distortion（air gap a=12 mm）

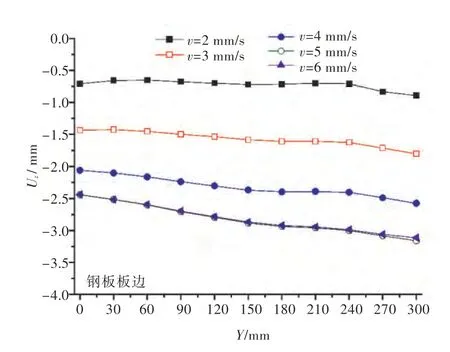
图11 加热线上各等间距节点的Z 方向位移图（12 mm 空气间隙）Fig.11 The Z direction displacement of equally spaced nodes along the heating line（air gap a=12 mm）

图12～图18 所示为在3 mm/s 加热速度、50 kW 加热功率的工艺参数条件下，通过改变空气间隙所得到的温度、变形结果图。其中，图12所示为钢板在3 mm/s 加热速度下，Y=150 mm 截面在感应加热器中心经过截面正上方时厚度方向的温度云图。图13、图14 分别为在3 mm/s 的加热速度下，钢板最终的横向收缩量云图和垂向位移云图。由图15 可见，随着空气间隙的提高，截面中厚度方向的加热深度越来越浅。由图16 可见，钢板的横向收缩量随着空气间隙的减小反而增大。由图17 可看出，随着空气间隙的增大，钢板的横向角变形逐渐增大。由图18 中可见，加热线节点的垂向位移与横向角变形一致，是随着空气间隙的增大而增大。分析图15～图18 可以得到与图8～图11 一致的结论，钢板加热深度增大后，厚度方向的温度梯度会减小，有利于横向收缩变形。

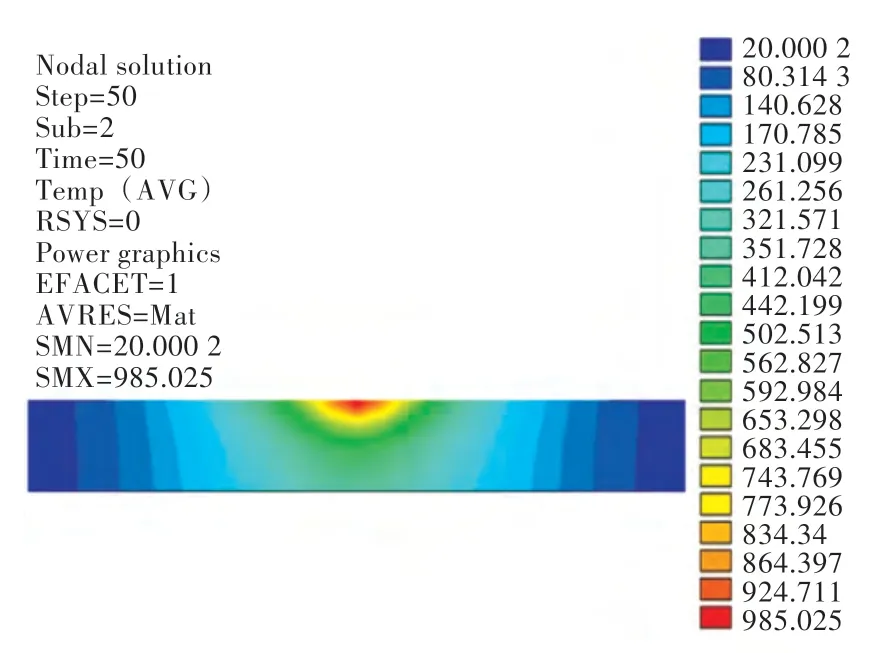
图12 Y=150 mm 截面温度云图（3 mm/s 加热速度）Fig.12 Temperature contours of Y=150 mm section（heating rate v=3 mm/s）

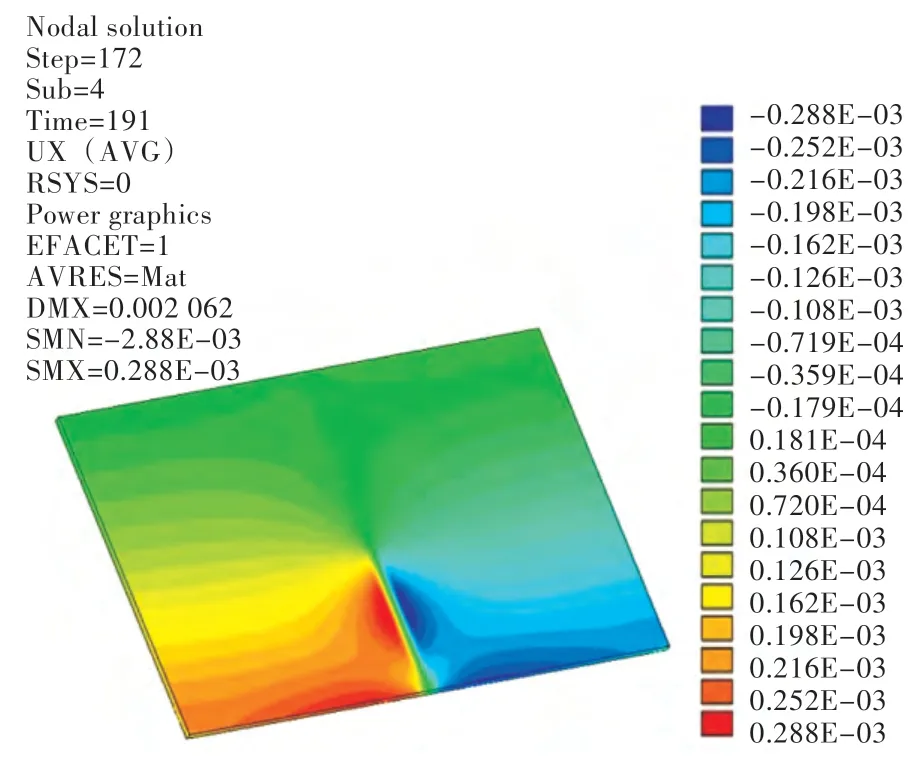
图13 横向收缩云图（3 mm/s 加热速度）Fig.13 The contours of transversal shrinkage（heating rate v=3 mm/s）

图14 垂向位移云图（3 mm/s加热速度）Fig.14 The contours of vertical displacement（heating rate v=3 mm/s）

图15 Y=150 mm 截面厚度方向温度分布图（3 mm/s 加热速度）Fig.15 The temperature distribution of Y=150 mm section in the thickness direction（heating rate v=3 mm/s）

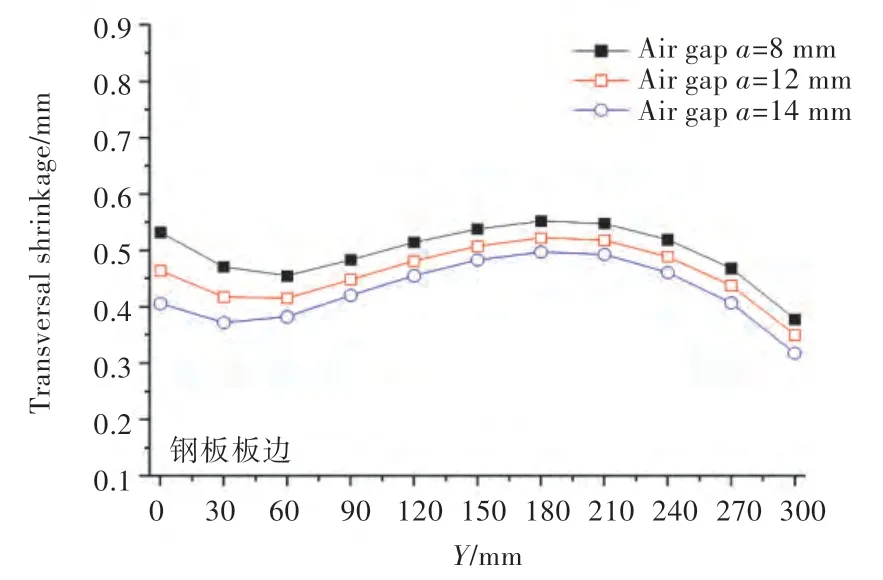
图16 横向收缩量分析图（3 mm/s 加热速度）Fig.16 The analysis chart of transverse shrinkage（heating rate v=3 mm/s）

图17 横向角变形分析图（3 mm/s加热速度）Fig.17 The analysis chart of transversal distortion（heating rate v=3 mm/s）

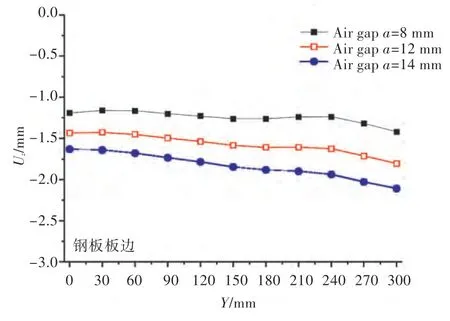
图18 加热线上各等间距节点的Z 方向位移图（3 mm/s加热速度）Fig.18 The Z direction displacement of equally spaced nodes along the heating line（heating rate v=3 mm/s）

综合分析图5～图18，可以得到以下结论：

1）改变加热速度与空气间隙这两个工艺参数，对横向收缩量、横向角变形和垂向位移值的总体分布趋势影响不大。

2）加热速度与空气间隙这两个工艺参数对钢板的加热深度具有直接影响。在钢板最高温度超过居里点温度（720 ℃）后，若钢板的加热深度浅，则厚度方向上的温度梯度大，较大的温度梯度有利于横向角变形和垂向位移；反之，加热深度越深，焰道加热区域上的钢板金属受四周冷却金属的挤压，主要会发生横向收缩变形。

3 横向收缩量回归模型及预测

本文利用数学回归方法得到了横向收缩量与主要工艺参数间的函数关系，回归计算中的横向收缩量值取各点的平均值。按照表6 的设计方案进行数值计算，得到的横向收缩量变形结果如表7 所示。

表7 数值设计方案的计算值Tab.7 Simulation results of numerical test conditions

参照Bae 等［11］提出的方法，假定横向收缩量和加热速度与空气间隙之间满足指数函数形式

式中：δ 为横向收缩量值；v 为感应器移动速度；a为感应加热器与钢板间的空气间隙。 γ，α，β为待求参数。

针对式（1）采用在方程两边取对数的方法得

式中：ϕ=ln δ；σ=ln γ；η=ln v；φ=ln a。通过上述转化，多元指数函数转化成了多元线性函数，采用SPSS 统计软件进行多元线性回归分析，得到α=-0.623，β =-0.312。

此时，将v-0.623a-0.312作为一个自变量看待，进一步修正式（1），假定v-0.623a-0.312单自变量参数与横向收缩量之间满足直线方程的函数关系

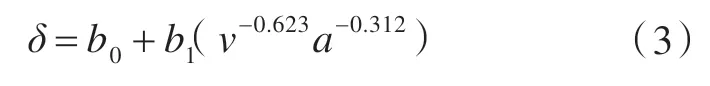
再次采用SPSS 统计软件进行直线方程的拟合，得到b0=0.002，b1=2.037。进而可得到横向收缩量和加热速度与空气间隙之间的函数关系

拟合直线的样本测定系数R 方值为0.973，接近于1，说明预测模型与数值模拟点的拟合度较好。同时，对该回归模型进行显著性检验，统计量的观察值F=473.422，而F0.01（1，13）=9.07，F＞＞9.07，可见线性回归方程在显著性水平为0.01 下十分显著。图19 所示为推导得到的回归曲线与数值计算点的分布图。将数值计算数据与回归数据进行对比，发现两者的平均相对误差为3.74%，相差较小。如表8 所示，通过式（4）计算出的预测值经与表5 中试验号为1～6 的试验值进行对比，发现平均相对误差为25.70%，预测值与试验值间的最大误差为0.15 mm，在工程允许的误差范围内，表明本文所提的回归模型可用于定工艺参数条件下的钢板横向收缩变形预测。

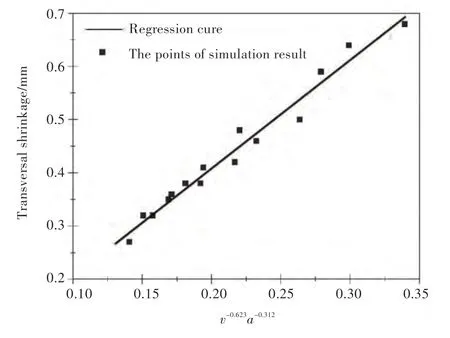
图19 回归曲线与数值模拟计算点Fig.19 Regression curve and the points of simulation results

表8 预测值与试验值的比较Tab.8 Comparison of prediction values and experimental values

4 结 论

本文进行了钢板移动式感应加热的正交分析试验，综合分析了3 个工艺参数对温度和变形的影响。通过进一步的数值分析，探讨了加热速度和空气间隙这两因素对横向收缩量、横向角变形和垂向位移值的影响，推导出了横向收缩量与工艺参数间的数学模型。

1）加热速度和空气间隙是决定钢板变形的主要影响因素，加热功率是次重要影响因素。钢板表面的加热温度主要取决于电磁感应原理，即当空气间隙处于感应器和钢板电磁耦合范围内时，钢板表面集肤层内的金属温度均可达到720 ℃以上，这是经过试验验证的。

2）加热速度和空气间隙影响钢板感应加热时厚度方向的加热深度，从而影响横向收缩量、横向角变形和垂向位移值的大小。

3）横向收缩量与v-0.623a-0.312之间存在线性函数关系，经对比预测数据与试验数据，发现平均相对误差为25.7%。

［1］LEE K S，EOM D H，KIM S W，et al.A Study on tem⁃perature distribution and curved structure for thick plate by single-pass induction heating［C］//NUMI⁃FORM 2010：Proceedings of the 10th International Conference on Numerical Methods in Industrial Form⁃ing Processes，2010.

［2］ZHANG X，YANG Y，LIU Y. Feasibility research on application of a high frequency induction heat to line heating technology［J］. Journal of Marine Science and Application，2011，10（4）：456-464.

［3］罗宇，江晓玲，邓德安.材料力学性能对高频感应弯板成形的影响［J］.材料工程，2005（8）：35-38.LUO Yu，JIANG Xiaoling，DENG Dean. Influence of mechanical properties of materials on high frequency linducting plate bending［J］. Journal of Materials Engi⁃neering，2005（8）：35-38.

［4］PANTELYAT M G，FELIACHI M. Magneto-thermoelastic-plastic simulation of inductive heating of metals［J］. The European Physical Journal Applied Physics，2002，17（1）：29-33.

［5］周宏，罗宇，蒋志勇.船舶板材几何尺寸的变化对高频感应弯板成形的影响［J］. 舰船科学技术，2009，31（9）：22-30.ZHOU Hong，LUO Yu，JIANG Zhiyong. Influence of geometry of ship panel on high frequency inducting plate bending［J］. Ship Science and Technolog，2009，31（9）：22-30.

［6］LEE K S，KIM S W，EOM D H. Temperature distribu⁃tion and bending behaviour of thick metal plate by high frequency induction heating［J］. Materials Research In⁃novations，2011，15（Supp 1）：283-287.

［7］LEE K S，EOM D H，LEE J H. Deformation behavior of SS400 thick plate by high-frequency-induction-heat⁃ing-based line heating［J］. Metals and Materials Inter⁃national，2013，19（2）：315-328.

［8］滕素珍，冯敬海. 数理统计学［M］. 4 版. 大连：大连理工大学出版社，2010.

［9］BIRK-SØRENSEN M，JENSEN J J. Simulation of welding distortion in ship section［D］. Denmark ：Tech⁃nical University of Denmark，1999：95-96.

［10］张安超，柳存根.水火弯板厚度方向温度场参数研究［J］.船舶工程，2011，33（增刊2）：148-151.ZHANG Anchao，LIU Cungen. Investigation on pa⁃rameters of the vertical temperature field of line heat⁃ing［J］. Ship Engineering，2011，33（Supp 2）：148-151.

［11］BAE K Y，YANG Y S，HYUN C M，et al. Derivation of simplified formulas to predict deformations of plate in steel forming process with induction heating［J］. In⁃ternational Journal of Machine Tools and Manufac⁃ture，2008，48（15）：1646-1652.