基于时频矩阵二值化的雷达信号分选

2014-02-06郭利荣何明浩郁春来王冰切

中国电子科学研究院学报 2014年5期

郭利荣，何明浩，郁春来，王冰切

(空军预警学院,武汉 430019)

0 引言

雷达信号分选是电子对抗领域中信号处理与应用重要而困难的研究课题，由于新体制雷达信号形式复杂、参数多变快变等，尤其是对于频率捷变、频率分集等信号，传统的基于常规特征参数[1, 2]和脉内特征参数[3, 4]的可靠性急剧下降，直接导致分选准确率的降低，出现分选“增批”、“漏批”问题。因此，许多学者致力于研究信号的特征，挖掘更有效的雷达信号特征，以实现对现代雷达信号高效准确的分选。

近年来，时频分析对雷达信号的处理方法受到广泛的运用，为雷达信号分选提供新的视角，具有重要的理论研究意义。文献[5,6]提出了应用时频分析对雷达辐射源信号进行分选的算法。文献[7]介绍了几种基于时频分析的信号特征提取方法，并未将提取的规律应用于信号分选之中。文献[8～10]研究了提取时频图像特征的方法，并将提取的特征参数应用于雷达辐射源信号分类识别中，但是图像特征提取算法的运算量较大。

从目前的研究成果来看，这些方法都具有特定的效果，但是对于新型复杂调制雷达信号分选，仍需进一步研究。对于频率捷变雷达来说，现用的都是采用相参体制，对于信号的相参特征，许多学者进行了相应的研究。文献[11]介绍了一种脉冲雷达相参测量的方法。文献[12]研究了雷达信号相参特征的数学模型，并利用FFT对该特征参数进行提取。文献[13]通过检测脉冲相位的线性度，实现了雷达辐射源信号的分选。

结合目前的情况，研究了一种基于时频矩阵二值化的频率捷变雷达信号分选新方法，有利于解决频率捷变雷达信号分选问题。在实际雷达应用中，不仅考虑频率捷变，还要考虑脉冲积累，对于这些雷达保持相位的关联至关重要。所以，为了高效准确的实现频率捷变雷达信号的分选，应用时频矩阵二值化的方法，提取能稳定表征频率捷变雷达相参与非相参脉冲信号的特征参数，最后采用支持向量机分类器对频率捷变雷达信号进行分选，验证了所提方法的可行性和有效性。具体流程如图1所示。

图1 时频矩阵二值化在信号分选中应用的流程图

1 频率捷变信号时频变换

时频分析之母是Cohen类时频分布，Wigner-Ville分布(WVD)是其中的一种，具有最简单的形式、理想的时频聚集性等优点[14]，反映了信号能量随时间和频率的分布，是针对非平稳信号处理的有效途径。雷达信号是典型的非平稳信号，因此，本文采用WVD对频率捷变雷达信号进行研究。侦收的信号为s(t)，将其采样后得到长度为R的离散序列s(n)，其离散WVD定义为[15]

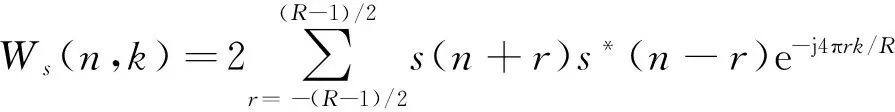
(1)

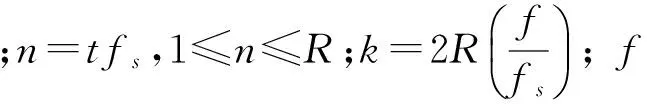
侦察接收到的频率捷变脉冲信号中，设Kij=Tij·fs为第i和j脉冲之间的采样点数，Tij=Tj-Ti为第i和j脉冲之间的时间间隔，经过采样得到第i和j脉冲的重构信号为

S=si+sj=ej(2πFi n+φi)+ej[ 2πFj(n+Kij)+φj]+υ(n)

n=0,1,…,N-1

(2)

假设不考虑式(2)中的噪声项，将其代人式(1)中，化简可以得到重构信号S的WVD为

2[ej2π(Fi-Fj)ne-j2πFj Kijej(φi-φj)+

e-j2π(Fi-Fj)nej2πFj Kije-j(φi-φj)]×

(3)

如果式(3)中脉冲i和脉冲j来自于同一部雷达，则脉冲i和脉冲j是相参的，即发射脉冲i和脉冲j的雷达辐射源的初始相位相同[12]，即脉冲i和脉冲j的初相具有稳定的关系，满足

(4)

式中，φ0为发射脉冲i和脉冲j的雷达辐射源的初始相位，τ=T0为侦察设备与雷达辐射源之间距离造成的信号传播时间延迟。则重构信号的WVD可以简化为

2[ej2π(Fi-Fj)ne-j4πFj Kijej2π(fi-fj)T0+

e-j2π(Fi-Fj)nej4πFj Kije-j2π(fi-fj)T0]×

(5)

无噪声情况下相参与非相参频率捷变脉冲信号WVD二维图，如图2所示。

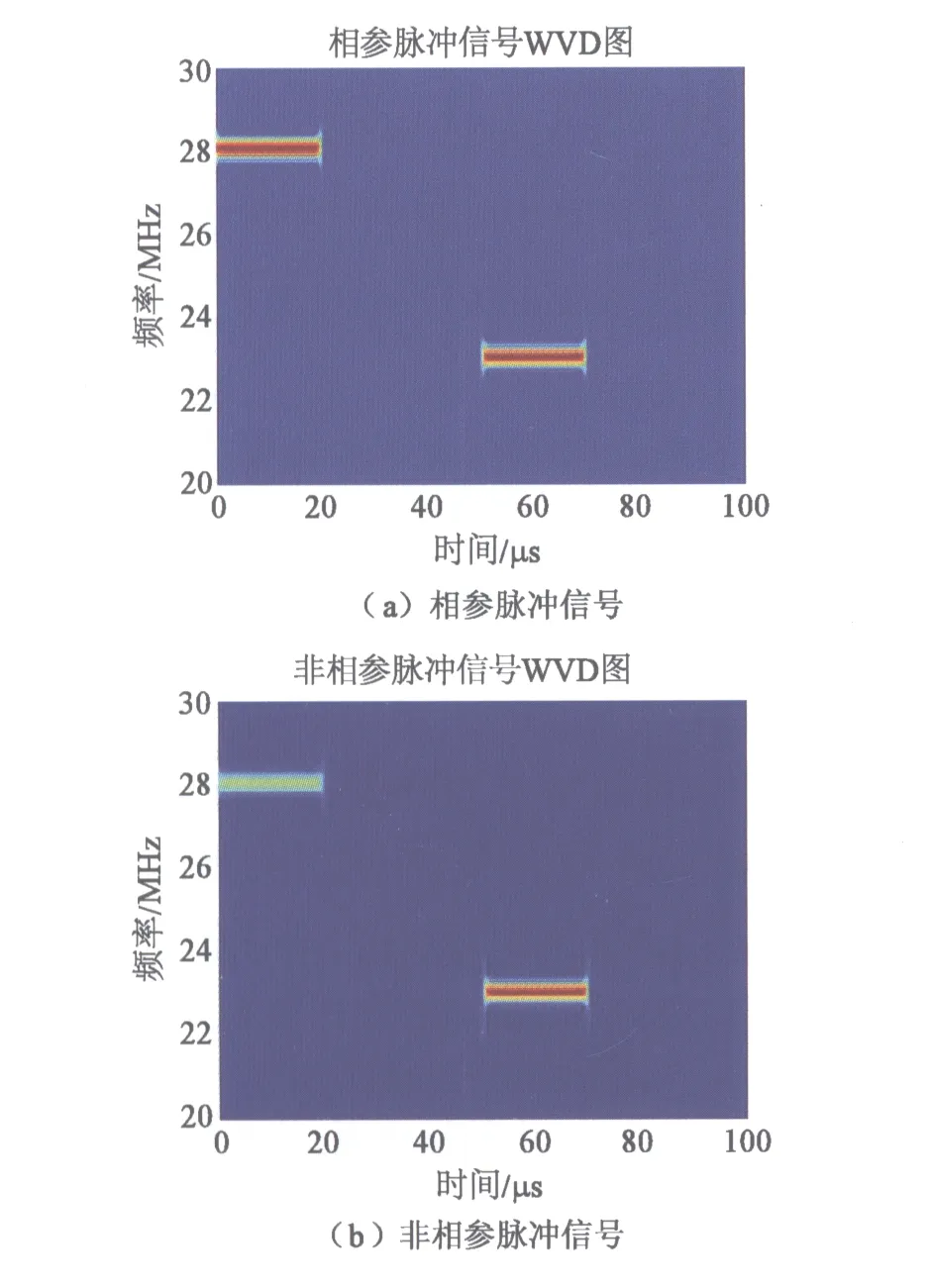
图2 频率捷变脉冲信号WVD二维图

由式(5)可看出，如果重构信号的两个脉冲是相参的，则重构信号进行WVD变换的结果，仅与雷达辐射源的初始相位φ0、脉冲采样频率fs、脉冲中频fs，归一化频率Fi和Fj、延时时间T0、脉冲采样点数R，以及两个脉冲之间的时间间隔Tij有关，当这几个参数确定后，重构信号WVD变换的幅度是确定的，两个脉冲的WVD变换结果是一致的，仿真结果如图2(a)所示。

如果式(3)中脉冲i和脉冲j来自于两部不同的雷达，即脉冲i和脉冲j是非相参的，则发射脉冲i和脉冲j的雷达的初始相位不相同，不满足式(4)中的关系。则重构信号的WVD变换结果是随机的，两个脉冲的WVD变换结果是不一致的，仿真结果如图2(b)所示。

由于时频变换的结果正比于信号的能量[16]，因此，相参与非相参信号在时频域的能量分布存在差异。对此可以进一步定量分析，提取信号能量在时频域的分布特征，应用于频率捷变雷达信号分选中。

2 时频矩阵特征提取

信号经时频变换后的结果主要以时频图像来表现，对于提取时频图像特征的算法运算量大，而直接从时频变换提取特征参数的难度较大。但对信号WVD变换后的时频矩阵进行处理，不仅可以减小特征提取算法的运算量，还可以降低特征提取的难度。因此，对WVD变换后的时频矩阵采用二值化进行处理，提取信号能量在时频域的分布特征。

2.1 矩阵二值化

时频矩阵二值化处理的主要思想就是将信号WVD变换后的时频矩阵W转为0、1矩阵，其目的是增加相参与非相参脉冲信号时频分析对比度，同时也可以减少后续特征提取的运算量，还可以减少其他冗余信息对时频分析的影响。时频矩阵二值化一般过程为：设定一个阈值T，将时频矩阵中所含的分量和阈值T进行逐一比较，时频矩阵中分量大于阈值T的记为1，小于阈值T的记为0，经时频矩阵二值化处理就可以得到一个0、1矩阵。其中，阈值T可以定义为[17]

(6)

式中，k是阈值T的可调系数；R是信号的长度；Wij是时频矩阵中第i行第j列个元素。

在实际信号处理应用中，不同信号WVD变换后的时频矩阵不同，阈值的设置是矩阵二值化的关键之处，且矩阵二值化方法的优劣对二值化效果具有重要影响，对后续的特征提取、信号分选都有密切的联系。因此，保证矩阵二值化的效果，才能得到较高的信号分选准确率。常见的二值化阈值的选取方法有整体阈值法、局部阈值法和动态阈值法[18]。

由于实际侦收的脉冲信号，其辐射源归属性不同，当脉冲中心频率发生变化时，各脉冲重构信号的WVD变换的结果不同。动态阈值法，即阈值的确定不仅取决于矩阵中的元素，还与矩阵中元素的位置有关。动态阈值法可以较好的根据实际处理的矩阵来设置相应的门限值。因此，采用动态阈值法可以较科学的确定阈值。

采用动态阈值法进行矩阵二值化处理的阈值处理方法为[19]：

(1)将时频矩阵W平均分成m个r×r的小矩阵；

(2)计算每一个小矩阵的平均值δn，其中n=1,2,…,m；

动态阈值法不仅可以保证二值化处理的效果，还具有较强的抗噪性。动态阈值法的关键之处在于区域大小的划分，区域大小的划分决定了算法的时间复杂度和空间复杂度。

时频矩阵二值化处理后得到0、1矩阵B为

(7)

2.2 相参特征提取

矩阵B中值为1的点代表能量超过阈值的元素点，即信号能量点。所以特征提取只需挖掘出能量分布情况所包含的相参特征。由于相参脉冲信号经时频变换后，在时频域上能量的分布近似相同，而非相参脉冲信号经时频变换后，在时频域上能量的分布显然不同。因此，只需要提取每个脉冲在时频面上的能量分布值，即

Pn=∑bij,bij∈第n个脉冲

(8)

再将提取的能量分布值进行归一化处理，即

(9)

式中，N为脉冲个数。

特征参数提取如图3所示。

图3 特征参数提取示意图

3 仿真实验及结果分析

3.1 特征提取效果分析

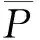
图4 不同信噪比下重构信号时频域能量分布归一化值

从图4中可以看出，两个相参脉冲信号在时频域的能量分布随着信噪比的增加趋于相同，当信噪比大于等于5 dB时，两个相参脉冲信号在时频域的能量分布归一化值几乎相等；两个非相参脉冲信号在时频域的能量分布随着信噪比的增加差距增大，当信噪比大于等于5 dB时，两个相参脉冲信号在时频域的能量分布归一化值差距变大，趋于稳定。因此，脉冲重构信号中各个信号时频域能量分布归一化值是否近似相等可以作为信号相参性的判别依据。可见所提取相参特征参数的效果与实验的预期效果一致，验证了特征参数提取方法是有效的、是可应用于对频率捷变雷达信号进行分选的。

3.2 分选仿真分析

仿真实验1：若侦察接收的一串脉冲信号中，经粗分选后，仍有六个脉冲信号无法区分来自哪几类辐射源。实际上，第一组：脉冲1、脉冲2和脉冲4来自同一辐射源的脉间频率捷变信号；第二组：脉冲3和脉冲6来自同一辐射源的脉间频率捷变信号；第三组：脉冲5来自单独一辐射源，脉冲幅度均为1，脉冲信号的中频分别为28 MHz、23 MHz、25 MHz、22 MHz、25 MHz、26 MHz，脉冲宽度均为20 μs，任意两个脉冲到达时间间隔为50 μs，采样频率70 MHz，发射相参脉冲1、2和4的雷达辐射源的初始是相同的，发射相参脉冲3和6的雷达辐射源的初始相位是相同的，发射三组脉冲的三个辐射源初始相位是不同的。在信噪比为10 dB情况下，对任意两个脉冲重构信号时频域能量分布值进行提取，进行100次Monte-Carlo实验，共计600个实验样本，其中240个样本作为训练的预测测试集，其余360个样本作为实际测试集。每次实验按照前文所所述的方法进行信号WVD时频变换，提取时频分析矩阵的相参特征，最终将特征参数输入到分类器中完成信号分选任务。

杨秉奎提高声音:“我过去了啊!”说着,便扯下一条麻袋,走到“隔墙”那边,见上海女知青周萍缩在一个角落,双手捂脸,继续哭着。

由于实验的样本数有限，对解决小样本、非线性问题中，支持向量机分类器表现出结构简单、全局最优、泛化能力强等独特的优势[20]，故采用支持向量机分类器对频率捷变雷达信号进行分选。实验具体步骤如下。

(1)选取侦察设备接收到的脉冲流中任意两个脉冲信号，并进行脉冲信号重构；

(2)对重构信号进行WVD变换，得到时频矩阵；

(3)对时频分析矩阵进行二值化处理，提取在时频域信号能量分布特征；

(4)将提取的特征参数输入到支持向量机分类器中，实现频率捷变雷达信号的分选。

支持向量机分选结果图，如图5所示。

图5 支持向量机分选结果图

从图5中可以看出信噪比为10 dB情况下，支持向量机分类器的预测分类与实际测试结果几乎一致，只有极少部分预测测试样本与实际测试集(训练样本)不一致，支持向量机分类器输出的结果为97.33%。因此，所提的方法可以实现频率捷变雷达信号高效准确的分选，验证了该方法的可行性和有效性。对于来自哪个辐射源，仍需要进一步的识别。

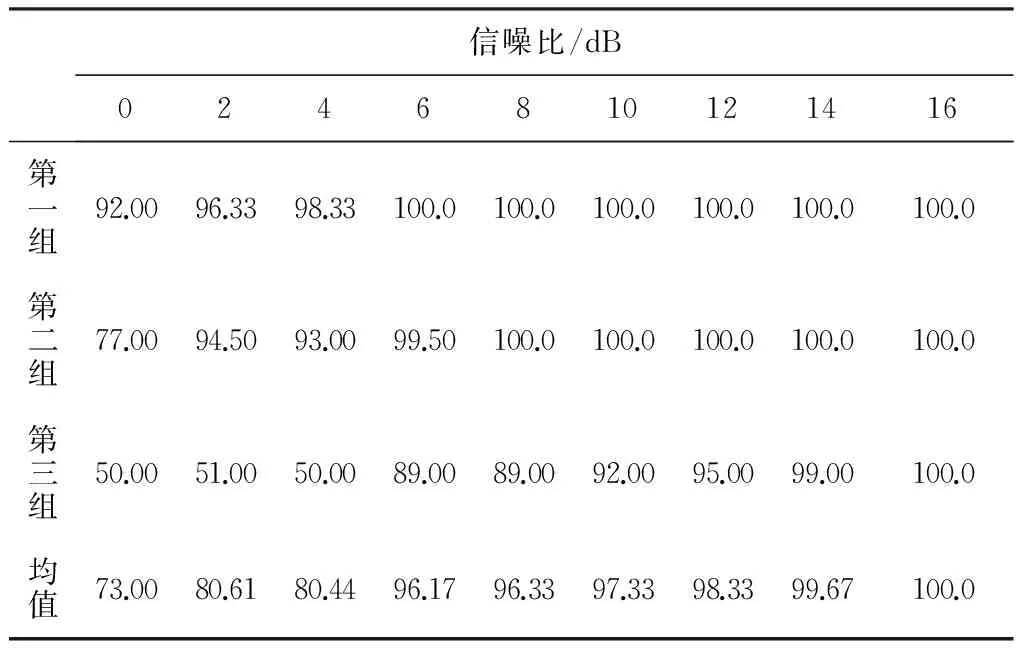
表1 不同信噪比下信号分选准确率(%)

从表1中可知，随着信噪比的增加分选准确率逐渐增大，当信噪比为2 dB时，信号分选平均准确率保持在80.61%以上，当信噪比达到6 dB时，分选正确率达到96.17%以上。第一组中有三个相参脉冲信号，第二组中有两个相参的脉冲信号，第三组中只有一脉冲信号，三组脉冲信号之间是非相参的，对三组脉冲信号的分选准确率进行比较，可知具有相参特征的第一和第二组脉冲信号分选准确率比第三组的高。由此可见，所提出的方法具有一定的抗噪性，在较低信噪比下仍保持较高的分选准确率，提取的特征可作为信号相参特征即新的信号分选特征参数，应用于频率捷变雷达信号分选中。

4 结语

相参与非相参脉冲信号在时频域的能量分布差异度较大，对时频变换结果即时频分析矩阵进行二值化处理，提取了脉冲信号在时频域的能量分布特征，即相参特征。通过仿真可知，该方法在小样本及较低信噪比下，可以实现频率捷变雷达信号高效准确的分选，说明采用时频矩阵二值化方法在频率捷变雷达信号分选中的应用是有效的、可行的。下一步可以结合提取的特征参数进一步研究快速分选算法，以更好的适应复杂电磁环境下对频率捷变雷达信号实时、准确的分选。

[1] 张什永,胡泽宾,王俊文.基于变换谱相干积累的片段信号PRI检测[J].雷达科学与技术,2012,10(3):286-289.

[2] 徐欣,周一宇,卢启中.雷达截获系统实时信号分选处理技术研究[J].系统工程与电子技术,2001,23(3):12-15.

[3] 张葛祥,胡来招,金炜东.雷达辐射源信号脉内特征分析[J].红外与毫米波学报,2004,23(6):477-480.

[4] GEXIANG Z,LAIZHAO H,WEIDONG J.Resemblance Coefficient Based Intrapulse Feature Extraction Approach for Radar Emitter Signals[J].Chinese journal of electronics,2005,14(2):337-341.

[5] MORAITAKIS I,FARGUES M P.Feature Extraction of Intra-pulse Modulated Signals Using Time-frequency Analysis[C]//MILCOM 2000.21st Century Military Communications Conference Proceedings,2000.

[6] UMAPATHY K,KRISHNAN S,JIMAA S.Audio Signal Classification Uusing Time-frequency Parameters[C]//Multimedia and Expo,2002.ICME'02.Proceedings.2002 IEEE International Conference on,2002.

[7] 赵拥军,黄洁.雷达信号细微特征时频分析法[J].现代雷达,2003,25(12):26-28.

[8] 龚文斌,黄可生.基于图像特征的雷达信号脉内调制识别算法[J].电光与控制,2008,15(4):45-49.

[9] 冀贞海,朱伟强,赵力.基于时频分布图像和主分量分析的脉内调制识别算法研究[J].电路与系统学报,2009,14(2):22-26.

[10] 邹兴文,张葛祥,李明,等.一种雷达辐射源信号分类新方法[J].数据采集与处理,2009(4):487-492.

[11] 张鹏.脉冲雷达的相参测量[J].现代雷达,2008,30(1):97-99.

[12] 孙鹏.雷达辐射源信号相参特征建模及提取技术研究[D].武汉:空军雷达学院,2011.

[13] 郭利荣,何明浩,郁春来,王冰切.基于脉冲相位线性度的雷达辐射源信号分选[J].中国电子科学研究院学报,2014,9(1):50-54.

[14] 何明浩.雷达对抗信息处理[M].北京:清华大学出版社,2010.

[15] L C.Time-frequency Analysis:Theory and Applications[M].Upper Saddle River:Prentice Hall Press,1998.

[16] 李宏坤,周帅,黄文宗.基于时频图像特征提取的状态识别方法研究与应用[J].振动与冲击,2010,29(7):184-188.

[17] 陈雕,张登福,雍霄驹,等.雷达信号时频分析的特征提取[J].计算机应用,2012,32(7):2063-2065.

[18] 吴冰,秦志远.自动确定图像二值化最佳阈值的新方法[J].测绘学院学报,2001,18(4):283-286.