对两类未定式极限求解方法的几点思考
2014-02-03范云晔
范云晔
(江苏城市职业学院,江苏无锡,214011)
对两类未定式极限求解方法的几点思考
范云晔
(江苏城市职业学院,江苏无锡,214011)
对于两类基础未定式:“”型以及“”型未定式的极限,通常是通过洛必达法则求解。但是其中存在一些题型若直接利用洛必达法则进行求解,会使解题过程复杂难解甚至无法求出。此时可以利用初等变换中的恒等式和等价无穷小,将未定式式子进行相应的变化,从而使极限的求解过程简化。
“”型和“”型未定式的解法;洛必达法则;初等恒等变换;等价无穷小
极限是高等数学的基础课程之一,是数学分析的重要基础,对该课程后续知识导数、积分等知识的学习起着至关重要的作用。而在学习极限时,未定式极限的求解方法又是学习的重中之重,并且所有的未定式最终都要转换为“”型和“”型未定式进行极限求解。在高职高专相关教材中,这两类未定式极限求解的知识都是通过利用洛必达法则求解的限。同时,大多数教材在安排该方面知识的求解例题时,大都列举一些直接利用洛必达法则就能够解决的例子,而对于直接利用洛必达法则解决比较复杂或无法解决的例子,则很少有教材提及,这就造成这样一种假象:凡是求“”型和“”型未定式极限的题目,只要使用洛必达法则就能很快解决,而且必定能够解决。
一、用初等变换的恒等式变化未定式式子直接求解极限
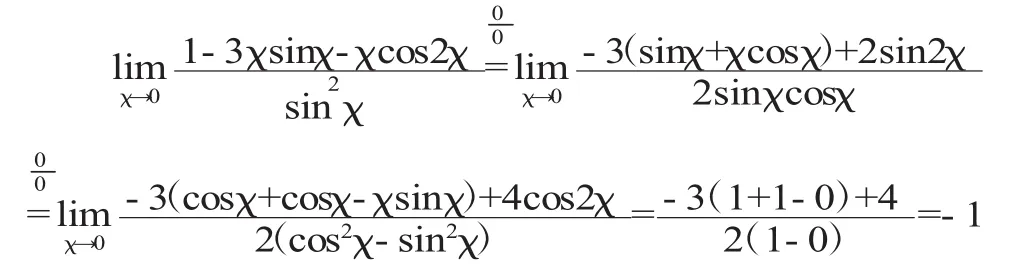
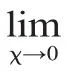
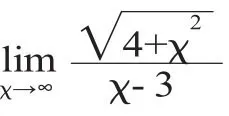

等恒等变化改变式子,再利用极限的基本公式和四则运算计算出该未定式的极限。如若不行,那么再考虑洛必达法则或其他方法来解决。
二、用等价无穷小公式变换未定式中无穷小量简化极限求解
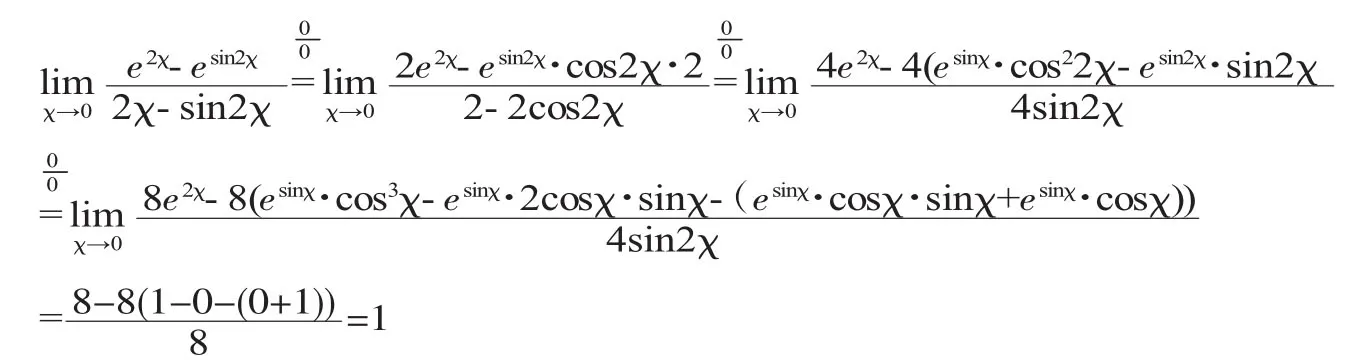
从求解过程可以看出,其中复合函数求导法则的使用一次比一次复杂。其实,对未定式作一个简单变形后利用等价无穷小的公式:em·χ-1□m·χ(m≠0,χ→0),作一个等价变换,极限就很容易看出了。
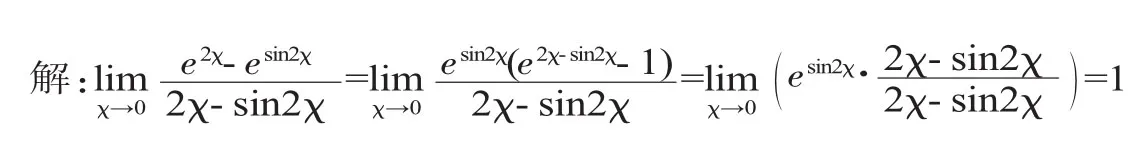
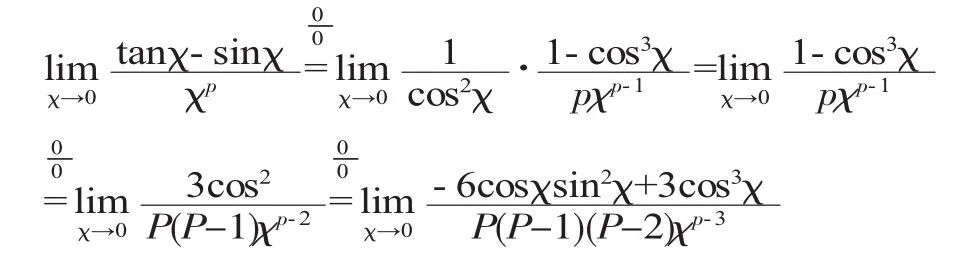
∵χ→0时,-6cosχsin2χ+3cos3χ→3
∴要使极限存在,则P(P-1)(P-2)χp-30
而要使得P(P-1)(P-2)χp-30,只能时P-3=0∴P=3
从出题的形式来讲,似乎该题就是考察是否掌握洛必达法则使用的前提条件。“在使用洛必达法则时,必须检查所求极限是否是‘’型(或‘’型)未定式,特别是连续使用洛必达法则时必须每一次都检查”,使用两次洛必达法则后就能判断出不能再次使用洛必达法则,再根据相关条件由结论倒推可得到该题的解。其实此题只需利用两个等价无穷小转换后,答案就已出来。
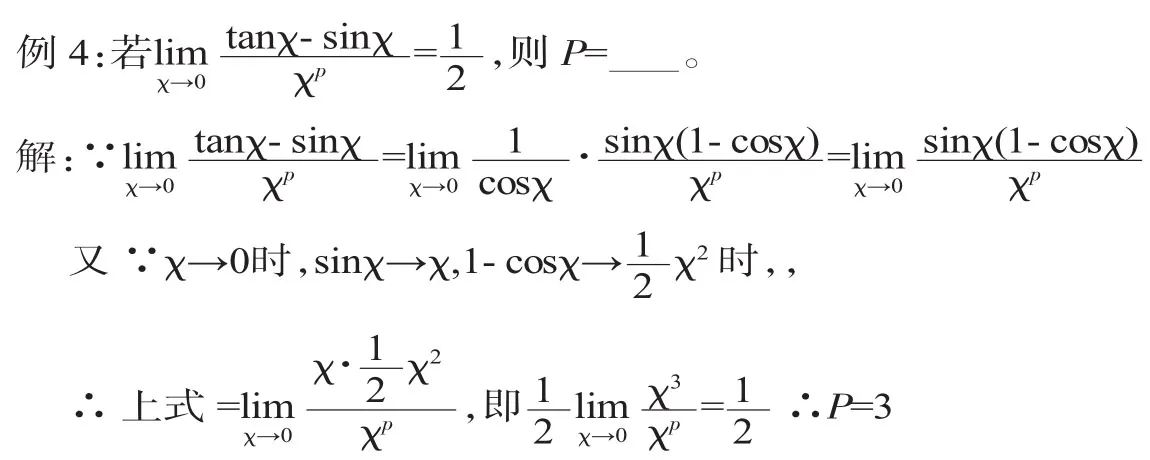
三、洛必达法则与初等变形或等价无穷小相结合,求解未定式极限
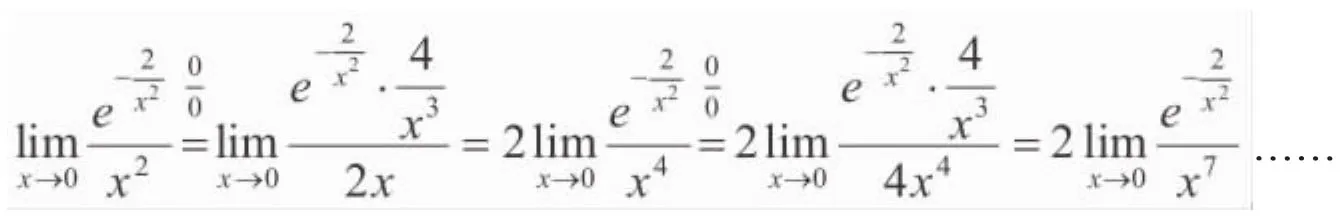
这样极限肯定没法求出。但是,只要先将未定式中的因式作一个简单代换后,再利用洛必达法则求解,则该极限就能迅速地求出。
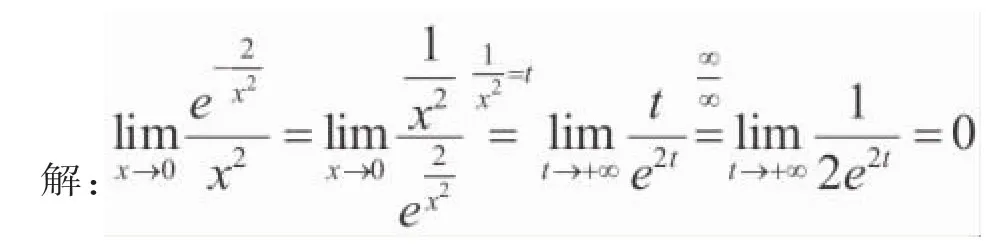
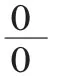
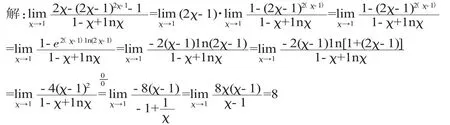
其实此未定式极限的求解,就是先通过对分子的拆分和变形将超越函数(2χ-1)2(χ-1)转换为e2(χ-1)1n(2χ-1)初等函数,再利用两个等价无穷小变换χ→1时1-e2(χ-1)1n(2χ-1)最后使用洛必达法求出该“”型未定式极限。同时可以发现该例在使用初等变形时并没有马上使未定式的式子化简,反而变得较为复杂,但是通过两次复杂等价无穷小变化后未定式的式子就被简化了,再使用一次洛必达法则将该极限求出。
总的来说,所有未定式极限求解都可以通过相应的恒等变化转换为“”型和“”型未定式极限的求解,洛必达法则对于这两类基础未定式极限求解是非常重要的,将其视为求解这两种未定式极限的通法通则。对于一些直接使用洛必达法则求解比较复杂的或无法求解的“”型和“”型未定式极限,可以利用初等恒等变换以及利用等价无穷小来简化未定式式子后,再根据实际使用求解极限求解的基本公式和基本法则,或者继续灵活结合洛必达法则来求解。
[1]叶惠英.数学(第四册)[M].南京:江苏教育出版社.2012:61.
[2]同济大学等编.高等数学(上册)[M].北京:高等教育出版社.2004:139.
编辑 郑晶
G642
A
2095-8528(2014)02-125-04
2014-09-11
范云晔(1977-),男,江苏无锡人,江苏城市职业学院讲师,硕士,研究方向为高职数学教育。
