解析法：命制几何试题的一种有效方法——以2014年北京市一道中考试题为例

☉宁夏回族自治区中卫市沙坡头区宣和镇张洪学校 张 宁

解析法：命制几何试题的一种有效方法
——以2014年北京市一道中考试题为例

☉宁夏回族自治区中卫市沙坡头区宣和镇张洪学校 张 宁

一、试题及解答

（1）求证：四边形ABEF是菱形；

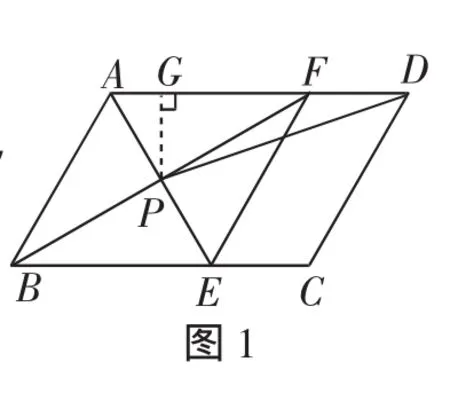
点评：本题以学生熟悉的平行四边形为背景，主要考查角平分线的性质、平行四边形的性质、菱形的判定和性质、含有30°角的直角三角形的性质、等边三角形的判定和性质、勾股定理的判定、等腰三角形的判定、锐角三角函数等众多基础知识，是一道基础性试题.对于问题（1），除了上述解法之外，还可先证明AE⊥BF，再证明AP=PE，BP=PF，从而证明四边形ABEF是菱形.对于问题（2），求解的思路与方法也不至一种，具有不同认知特征的学生可用不同的思路求得结果.

在问题（2）的条件下，本题还蕴藏着丰富的结论.

二、利用解析法探索新结论

如图2，设PC与EF相交于点N，则易求得EN=1.

三、根据新结论命制新试题

（1）求证：四边形ABEF是菱形.

（2）当AB＝4，AD＝6，∠ABC＝60°时.

①请判断PM与MD的大小关系，并说明理由；

②求FM的长度.

命题意图：通过本题主要考查的知识点有平行四边形的性质、角平分线的性质、三角形中位线的性质、全等三角形的判定与性质等.

解法提示：（1）略.

（1）求证：四边形ABEF是菱形；

（2）求EN的长度.

命题意图：通过本题主要考查的知识点有平行四边形的性质、角平分线的性质、平行线的性质、菱形的判定与性质、三角形中位线的性质等.

解法提示：（1）略.

（2）如图9，连接PD，由例2知，FM=1.由三角形中位

四、结束语

解析法不仅是一种解题方法，它在命题技术中同样具有重要作用.利用解析法可快速发现几何图形中线段的大小关系、直线的位置关系、点与直线的位置关系等，利用这些新结论可命制出新颖的几何试题.在命题时一定要结合学生的认知特点，合理设置已知条件及问题，命制的试题在解答过程中也要符合《义务教育数学课程标准》（2011年版）的要求.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.张宁.以“共顶正方形”为模型的中考试题及变式探究［J］.中学数学（下），2014（4）.FH