让解题思路来的更自然些——从两道高考题说起

☉浙江省象山中学 祝益锋

让解题思路来的更自然些
——从两道高考题说起

☉浙江省象山中学 祝益锋

笔者在做2013年辽宁高考卷（理科），发现辽宁两道压轴题考生得分不高，笔者认为得分低的主要原因是学生未能较好的掌握通性通法，而这又是因为有相当一部分教师在教学或研究中有意或无意的显示自己在解题方面的“特技”，不注重对学生通性通法的指导，使学生受到潜移默化的影响所致，学生看到这些题目时首先考虑的不是通性通法，而是特殊技巧，思路混乱，解题时一旦遇阻就毫无章法.借此笔者谈谈在数学解题中怎样使解题思路自然而然地展开，少一些技巧，多一点自然.

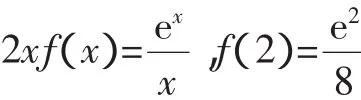
A.有极大值，无极小值

B.有极小值，无极大值

C.既有极大值又有极小值

D.既无极大值也无极小值

上述的解题思路说明一个道理：自然而然、水到渠成的解题过程，常常源自思维方法上的质朴！

（2）若f（x）≥g（x）恒成立，求实数a的取值范围.

本文主要分析第（2）问，我们先看给的标准答案（摘录部分）如下：

感悟：《数学新课程标准》明确指出：“注重提高学生的数学思维能力.”人们在解决问题时，经历了猜想，再着手验证的过程，从局部到整体，层次分明，逐次渐进，并且后者与前者有密切的逻辑联系，就像爬坡一样拾级而上.思路也随着问题的出现而逐渐深入，但每步都是那么自然和顺利成章.当我们遇到“难题”和新颖的试题而一筹莫展无从下手时，不妨先把问题简化一下，以突出其关键信息，特别地“把一个比较复杂的问题，‘退’成最简单最原始的问题，把这个最简单、最原始的问题想通了、想透了”，然后再归纳、综合而实现飞跃，“这是学好数学的一个诀窍”.解答任何一个有困难的数学问题都应该从简单的情形开始！教育数学的先行者张景中院士一向主张为教育而数学，改造数学使之更适宜于教学和学习，解题数学何尝不是这样，让解法是自然的，平易近人的.

但是，有些教师在解题中过于渲染解题技巧，至于技巧怎么来的，其中又蕴含着怎样的数学思想方法，往往不作解释，或语焉不详，让人只能停留在“欣赏”层面，不会产生心领神会的心灵共鸣.笔者认为从基本概念、原理出发，以基础知识为依托、以基本方法为技能，按照既定的步骤，逐步推出问题和解答，解法思想顺乎一般思维规律，其具体操作过程应该为多数学生所掌握.

题3（2008年浙江高考第8题改编）已知cosα+2sinα=，求tanα的值.

许多文章都对此题做了多种解答，不乏有精彩的，但又有些值得商榷，比如有导数法，左右两边求导得出，-sinα+2cosα=0，tanα=-2，马上得出结果，解法之快，不得不佩服，但此方法是否具有“普适性”呢？请看下面同样是浙江省的高考题：

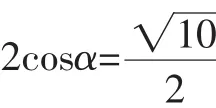
如果用导数法，此方法在此题中就失灵了.这两题都是考查基本的两角和正、余弦公式，所以自然的想法就是逆用正、余弦公式，解法如下：

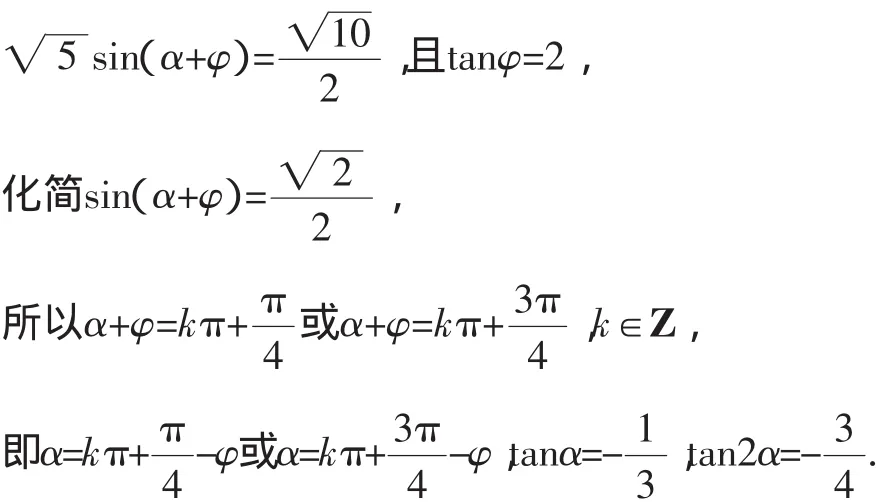
当然还有其他解法这里不再例举.

正如著名数学史学家M.克莱因曾说，“把函数的连续性说成是一条可以用铅笔不间断移动所画出的曲线，比起ε-δ的定义来，要容易掌握得多啊！”，“数学学科并不是一系列的技巧，这些技巧只不过是它微不足道的方面：它们远不能代表数学，就如同调配颜色远不能当作绘画一样.技巧是将数学的激情、推理、美和深刻的内涵剥落后的产物.”

用最简单的、最直观的方法说明最深刻的道理，才是数学之精髓，才是大道.

1.王芝平，王敬华.让解题思路来的更自然一些［J］.数学通报，2013（2）.

2.章建跃.注重通性通法才是好数学教学［J］.中小学数学（高中版），2011（11）.