关于高中数学导数公式的应用研究

☉广西省南宁市四十二中 农仕科

关于高中数学导数公式的应用研究

☉广西省南宁市四十二中 农仕科

高中新课标中，利用导数分析和解决问题，为导数应用价值的鲜明体现.导数在应用中始终贯穿着函数思想，且在应用领域呈现不断扩大的态势.新课改在对高考题目的考查中，有逐渐加强的态势.

一、导数公式的应用

1.用导数求函数的切线

导数的几何意义：曲线在某点处的导数值就是曲线在该点处的切线斜率，应用中注意函数在某点处可导，曲线在该点处一定存在切线，但是曲线在某点存在切线，却未必可导的特性.

例1 函数y=f（x）在点x0处导数的几何意义，就是曲线y=f（x）在点P（x0，y0）处的切线的斜率.在求解中，设曲线y=f（x）在点P（x0，y0）处切线的斜率是f′（x0），相应的切线方程为y-y0=f′（x0）（x-x0）.

在该例题的切线方程求解中，就是根据导数所体现的几何意义来求解的.

2.用导数判断函数的单调性

在平面直角坐标系中，导数代表的就是某条曲线在某一点的斜率.判断函数的单调性，就可以根据一个切线上的斜率来判定，斜率都大于零，那么可以准确判断出其单调递增的特征.尤其是在简单的一次函数中，当曲线斜率为正时，函数单调递增，反之为负时就是单调递减.

例2 一次函数y=kx-k在R上单调递增，则它的图象过第几象限？

解析：易知函数过定点（1，0），函数必过第一、四象限，又因为该函数单调递增，所以有k＞0，所以，该函数也过第三象限.综上所述，函数过第一，三、四象限.

从一次函数的单调性分析，函数图像是在导数的定义中引申出来的.由导数特性分析函数单调性，是确立函数与象限关系的着力点，同时也可引申出函数单调区间问题的解决策略.

例3 求函数f（x）=x3-3x+1的单调区间.

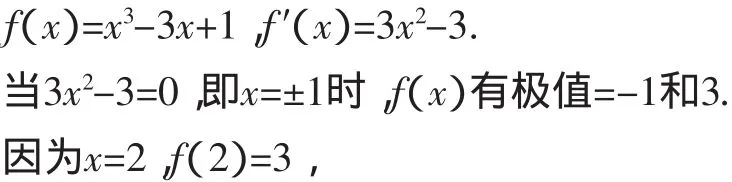
所以，函数在（-∞，-1］单调递增，在［-1，1］单调递减，在［1，+∞）单调递增.求解函数单调性，更可以显示导数公式的价值.在实际应用中，还可以延伸出导函数“二次型单调性问题”.

3.用导数求函数的极值

在例3中，已经凸显导数求函数极值的应用价值，在实施进一步探讨时，求解函数极值，也能从导数的零点入手加以应用.

例4 求f（x）=x3-12x的极值.

解：函数定义域为R.f′（x）=3x2-12=3（x+2）（x-2）.

令f′（x）=0，得x=±2.

当x＞2或x＜-2时，f（′x）＞0，所以函数在（-∞，-2）和（2，+∞）上是增函数；

当-2＜x＜2时，f′（x）＜0，所以函数在（-2，2）上是减函数.

所以当x=-2时，函数有极大值f（-2）=16，

当x=2时，函数有极小值f（2）=-16.

利用导数求解简单函数极值时，从方程f′（x）=0着手，在进一步探讨定义域内相关极值点时，就可准确地得到极值.

4.利用函数的单调性求参数的取值范围问题

这是从导数公式引申出来的问题，即在已知函数的单调性的条件下，求解参数的取值问题.这种问题的解决思路是在导数运算的基础上，利用函数的单调性求参数的取值范围问题.

若函数单调递增，则f′（x）≥0；若函数单调递减，则f′（x）≤0.

在已知函数的单调性的条件下，求解参数的取值问题是常见的题型之一，解决此类问题的方法主要是以导数的运算和性质求解参数的取值范围问题.

二、导数的实践应用价值

高中理科之间互相都有融合渗透，因为在物理学、几何学、经济学等学科中，一些重要概念都可以用导数来表示.从理科高三接触的微积分来分析，显示的自变量和变量之间的关系可以看出它应用的身影.当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限，在一个函数存在导数时，称这个函数可导或者可微分.可导的函数一定连续.不连续的函数一定不可导，这甚至可以被认为高中与高等数学衔接中最基础的定义.

在物理中，导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性问题.它有极其丰富的实际背景和广泛应用空间.它是研究增长率、膨胀率、效率、密度、速度、加速度等现实问题的科学.高中导数公式的应用过程，是让学生感知瞬时变化率的过程.导数的概念和导数公式的应用，正是实现由初等函数正常推导的过程，是从中规范导数实践教学的过程，也是深度理解和认识导数的过程.导数的实践应用事项，正是从导数的初等概念中衍生出来的，运用导数公式推导的过程，是巩固数学的过程，也是规范求解和感受导数公式魅力的过程.函数的导数实质是一个平均变化率极限问题，求解函数必须明确掌握求导公式，尤其是复合函数的导数求解问题.

三、近年来与导数相关的考试大纲要求

近年来高考考试大纲的考点，有许多都与导数有着千丝万缕的关系.从导数引申出来的考点比重的上升，使得导数与函数、微积分、复合函数、反函数、隐函数之间的共通性愈加明显，尤其是函数的导数和导函数，以及函数图像与导数特性的融合，导数和函数的考试范畴逐渐加大.导数的综合应用内容和形式的不断变化，都离不开导数公式的可变性和便捷性，离不开导数公式的应用.

在区间里判断函数图形的凹凸性时，导数就充当一个假想的角色，可以作为描绘函数图形的切入点.如在区间（a，b）内，设函数f（x）具有二阶导数.当f″（x）＞f（x）的图形是凹的；当f″（x）<0时，f（x）的图形是凸的.这是由导数应用凸显的用一元函数导数判断函数图形的凹凸性.

在初等函数的基本推导中从原函数到导函数之间的推导过程，显示了导数与函数之间的关系.导数的计算，要贯穿求导法则.

四、求导公式教后反思

从理解导函数概念出发，求解抽象化导函数，在课堂上，教师可以配置函数模型.让学生充分了解常数函数，一次函数，二次函数等概念，合理引导他们求解其导函数从形的角度借助图像展开教学，重视课堂反馈，重视高中生学习思维和心理特点.在理科班级教学中，要及时疏导学生学习困惑，迎合他们学习心理规律.引导他们学会借助图像弄清切线斜率的变化随x的变化情况，最后在脑海中自发的形成完善的解题思路，将复杂问题从简单立足点出发，实现题型互换，得到最初解决思路.

导数公式的使用过程，需要学生有充分的适应过程，是要学生统观推导公式全局，从巩固导数定义出发，增强高中生学习导数的信心和兴趣.在课堂中，平衡学生心理素质，及时形成共同学习的氛围，对于后进生，要从丰富他们的知识素养开始，开展帮扶制度，实现课堂节奏的一致性.

在教学中，运用导数推导的过程，必须把握其基本规律，按照具体的学习步骤，按部就班的实施教学，除了严格控制难度外，在高三阶段可适当与高等数学微积分接轨.从巩固导数概念做起，避免过量的形式化运算联系，及时纠正推导函数中的不足之处.让学生直观的理解导数背景、思想和作用，可以充分感受利用导数解决函数和实际问题的巨大作用，从而在导数应用思想上实现经久的价值.

在教学的难点方面，导数和导函数之间的概念问题，是必须重视的问题.在函数可导和连续性之间，实现导数应用的规范化，弄清函数的导数是因变量与自变量增量比之间的平均变化率，也是明确其可导性的有效方略.而导函数是相对于原函数而言存在的函数，是一个新函数在原区间的导函数，导数在期间只是一个值的作用.

五、结束语

导数在数学中的应用价值，主要显现为运用导数来求解函数切线、函数单调性、函数极值，不仅便捷还省时.高中数学导数公式集中反映了导数公式应用思想.导数是两个无穷小变量比的极限，反映函数的变化率.导数的几何意义是函数切线的斜率，在物理上体现瞬时速度.在结合课改和高中生身心发展现状时，要培养学生的辩证思想和掌握导数的变化趋势，成为导数应用领域必须关注的大事.这对于应用导数公式解决高中生日常数学难题，具有积极地指导作用.

1.王彩霞，浅谈三角函数的几种解法［J］.中学数学（上）.2012（8）.

2.王利，邓鹏.加强高中与大学导数公式知识的衔接［J］.数学学习与研究，2012（17）.

3.赵波.谈解答数学题的几种意识［J］.中学数学（上），2011（3）.

4.程守权.高效数学课堂的设计意图展现——案例分析“应用导数研究函数的最值”［J］.高中数理化，2012（2）.