一道课本习题教学的实践与思考——关于例、习题教学有效性的探讨
2014-02-01湖北襄阳市襄城区教研室张少艳
☉湖北襄阳市襄城区教研室 张少艳
☉湖北襄阳市第七中学 魏世勇
一道课本习题教学的实践与思考
——关于例、习题教学有效性的探讨
☉湖北襄阳市襄城区教研室 张少艳
☉湖北襄阳市第七中学 魏世勇
数学教学离不开讲题,如何讲题,才能真正体现例、习题的作用,凸显例、习题的价值?为此,我们通过“十分钟讲题”活动,对如何提高例、习题教学的有效性进行了一些实践和探索,旨在引导教师钻研教材,重视教材例、习题的研究与挖掘,切实提高例、习题教学的效率.现以课本一习题的教学设计为例,谈点儿体会,供参考.
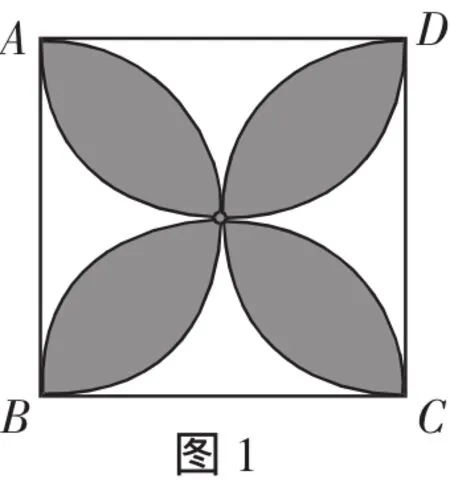
题目:如图1,正方形的边长为a,以各边为直径在正方形内画半圆,求所围成的图形(阴影部分)的面积S.
一、习题分析
本题是人教版九年级上册第114页习题24.4第3题,是在学生已学习了三角形、矩形、正方形、圆、扇形、弓形等图形的面积之后,给出的一道传统的经典习题,该题计算方法灵活多变且渗透了丰富的数学思想,深受历来教材编审者的青睐.立足此题,可归纳出求解阴影面积的常用方法.
题目的难点是解题方法的构思,即如何将阴影部分的面积化为规则图形面积的和或差,要求学生有一定的观察能力和计算能力.突破难点的关键是引导学生对图形进行适当的分割与转化.
学生从小学开始就经常接触到此类求阴影部分面积的题目,因此对解题方法并不陌生,但由于学习时碰到的不少题目都有一定的难度,要求学生有较强的观察能力,所以不少学生难免有畏难情绪,不愿意作深入思考.不过此类题目往往一点就透,看清楚后有一种豁然开朗的感觉,如果教师能适当加以引导,也极易调动学生的探究欲望.
二、教学设计
为方便起见,以下把阴影中两个小弓形组成的图形称作一个花瓣,每两个花瓣与正方形的一边之间的部分称作一个空白.
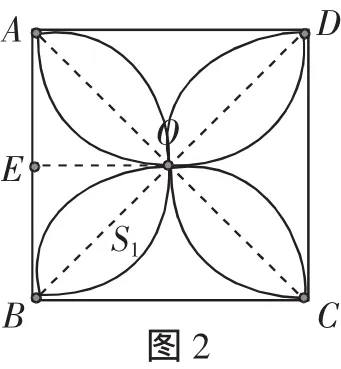
1.直接求部分阴影的面积
(1)求一个小弓形的面积.
分析:每个花瓣由2个小弓形组成,把阴影部分看成8个小弓形的和.可以计算一个小弓形的面积,然后乘以8,而一个小弓形的面积等于一个扇形减一个三角形的面积.
解法1:如图3,取AB的中点E.

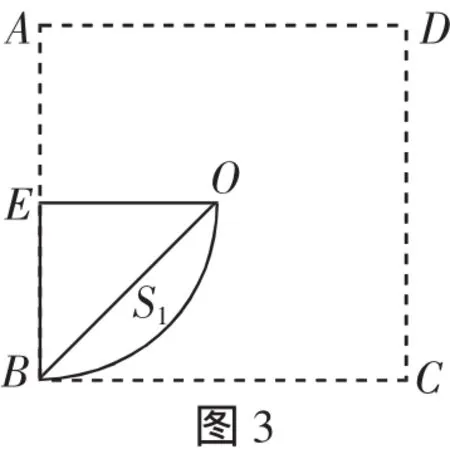
(2)求两个小弓形的面积的和.
分析:把两个小弓形的面积作为一个整体来看待,计算两个小弓形的面积S1+S2,然后乘以4.

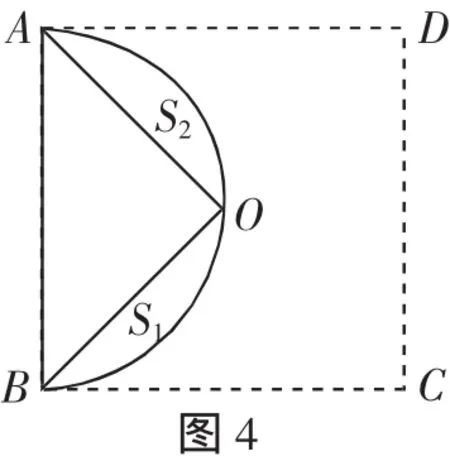
2.求空白的面积
(1)求半个空白的面积.
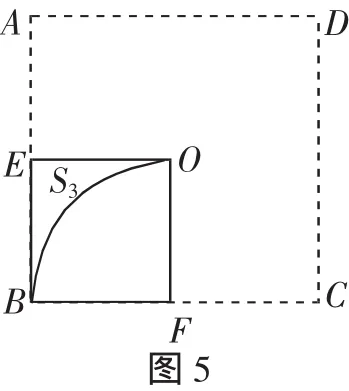
分析:每个空白由2个半个空白组成,把所有空白看成8个半个空白的和.可以计算半个空白的面积,用小正方形BEOF减去扇形FOB可求S3,然后乘以8,得到所有空白的面积,阴影的面积等于正方形的面积减去所有空白的面积.
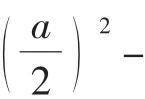
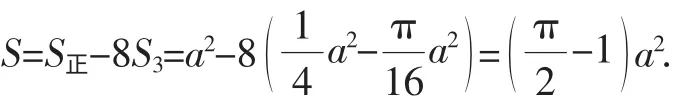
(2)计算2个半个空白面积的和.
分析:利用矩形的面积减去一个半圆的面积可以得到2个半个空白面积的和.

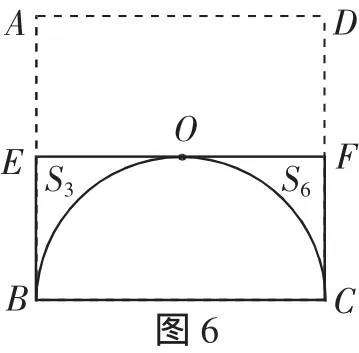
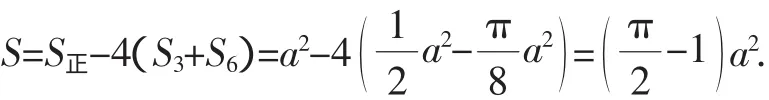
(3)求1个空白的面积.
分析1:利用曲边形AmOnCB的面积减去半圆的面积,从而得到一个空白的面积S4.由于该曲边形包含有两个空白,两个花瓣,所以它的面积是正方形的一半.

4.覆盖的方法
分析:用四个半圆去覆盖这一个正方形,其中阴影部分覆盖了两次.所以,4S半圆=S+S正.
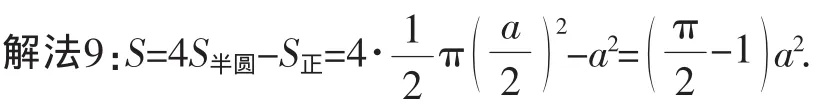
5.代数法
分析:设每个花瓣的面积为x,每个空白的面积为y,可列方程组.
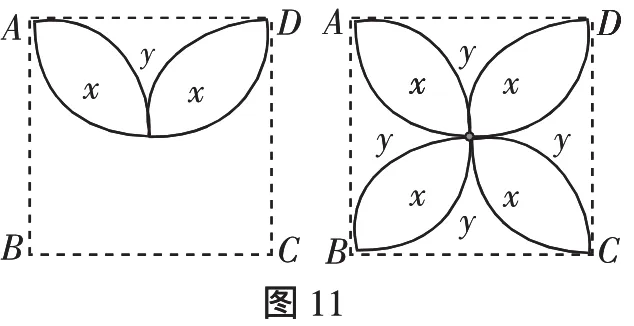
解法10:如图11,设每个花瓣的面积为x,每个空白的面积为y.
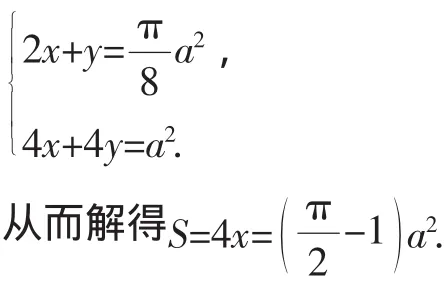
三、设计说明
1.归纳解题规律
通过直接求小弓形、间接求空白、割补、覆盖、设元等手段,归纳出求阴影部分面积的基本方法,即将组合图形的面积化为基本图形面积的和或差.通过多题一解,培养学生的观察,化归能力;通过一题多解,培养学生思维的广阔性和深刻性.通过该题诸多方法、规律的小结、梳理,以一当十,触类旁通.
2.渗透思想方法
通过适时小结,螺旋上升,使学生的思维在一定程度上趋于有序、条理化,同时也为一些新思路的出现作铺垫.求半个空白,2个半个空白,1个空白,2个空白的面积,就充分体现了转化的思想;把2个小弓形、2个半个空白或2个空白放在一起计算,又体现了整体思想;而阴影面积往往涉及复杂的数量关系,所以有时通过设元沟通,及时渗透方程的思想也是有必要的.
3.关注学生的易错点
不少学生受过去错误解题经验的束缚,或观察能力不够,缺乏对图形的精准把握,不能准确地把复杂图形转化为基本图形的组合,从而带来思路的错误,而方法选择的不合理容易导致运算量的增加,致使解题出错或出错的几率加大,因此在学生掌握基本方法的基础上,应引导学生灵活、合理地使用方法.当然,基本运算的过关是前提.
四、关于有效性的思考
1.注重技能目标的落实
数学基本技能是指关于数学的基本运算、作图(绘图)、推理、表达、操作和一些技巧等,是学生经历数学学习后直接可以获得的结果.帮助学生掌握必要的基本技能是数学教学必须达成的目标.例、习题不仅是教师讲课时用以阐明数学概念和数学命题的基础性材料,也不仅是数学知识转化为基本技能的附件,更重要的是它还是“解决问题”在数学课堂教学中的重要表现形式.
在例、习题教学中,教师应启发、引导学生思考和寻找眼前的问题与自己已有知识体验之间的关联,让学生经历回想、联想、猜想的探究过程,经历观察、实验、归纳、概括、演绎推理等思维过程,体验、琢磨解题的思路、方法、技能的形成过程.教师还要注意在知识与技能形成的关键处给学生以必要的引导和点拨,让学生在实践活动之后进行理性的总结归纳,课堂上留给学生独立思考和独立完成作业的时间,通过应用知识、训练形成技能.学生在知识和技能的不断掌握与迁移的过程中,认知结构逐步得以同化或改组,数学能力也相应得到了发展和提高.
2.注重解题方法的梳理与归纳
在例、习题教学过程中,应加强对学生学习方法的指导,尽量让学生积极主动地参与知识、方法的探究过程,通过自己的阅读、思考、观察、操作、探索、想象、质疑等丰富多彩的认识过程来获得知识,感悟数学思想,获得解题经验.
对解题方法进行梳理与归纳,就是学生的一个学习反思的过程,通过反思解决问题的可能性和有效性,让学生在自己的大脑中将知识与技能、过程与方法内化为自己的学习能力,享受情感与态度上带来的成功的快乐,就能有效地深化对知识的理解.对学生的发展而言,学习的价值不只是记住几个数学结论,解决几个习题而已,而是让学生在解决问题的过程中体会到解决问题是可以有不同策略的,这些解决问题的策略,渗透着数学的思想方法在里面.当学生能用自己的语言表达对问题的理解,对常见的数学思想方法有一定认识的时候,学生的思维才能真正得到升华.
3.关注数学思想方法的渗透
数学思想方法是数学的“灵魂”.“在解决具体问题中,数学思想往往起着主导作用,尤其是它对产生一个好‘念头’,一种好‘思路’,一种好‘猜想’提供了方向”.中学数学主要涉及的数学思想有:转化的思想,化简的思想,分类讨论的思想,数形结合的思想,函数与方程的思想,数学建模思想等.在例、习题讲解时,教师不仅要告诉学生有哪些数学思想和方法,它们各自有什么作用,而且更重要的是向学生展现数学思想和方法的产生、发展和应用的过程.著名数学家波利亚说:“一个专心钻研教材的老师能够拿出一个有意义的但又不太复杂的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”事实上,数学的很多思想方法都隐藏在课本的例、习题中,在教学中,教师如果能对课本上的例、习题进行必要的挖掘,往往会起到意想不到的效果,有利于学生知识的建构.
4.关注数学思维的养成
解题思维活动中充满着新旧认知结构的矛盾,已知与未知不断变化发展的矛盾,老背景与新情景的矛盾.若没有正确的思维,解题只能永远停留在模仿层次上.在教学中,教师应鼓励学生打开思维的翅膀,通过一题多解、一题多变,培养学生良好的思维习惯.本节课在处理求阴影部分的面积时,引导学生用五种不同的方法来解决问题,从不同的角度来思考问题,学生会学得有滋有味,思维、能力都得到提升.这样,学生掌握的将不是一道题的解法,而是一类题的解法.他们收获的不仅仅是知识,还有兴趣和思维.
例、习题教学是学生巩固知识、发展能力、掌握思想方法的重要渠道,让学生在潜移默化的例、习题探索过程中学会发现问题、提出问题,进而解决问题;领会数学的研究方法,学会数学地思考,从而达到“做一题,通一类,会一片”,体验“会当凌绝顶,一览众山小”的意境,才能游刃有余,以不变应万变.
这样,我们的课堂教学才会更有效.
附:反馈练习
1.如图12,正方形的边长为a,以各边为直径在正方形内画半圆,则图中阴影部分的面积S=_______.
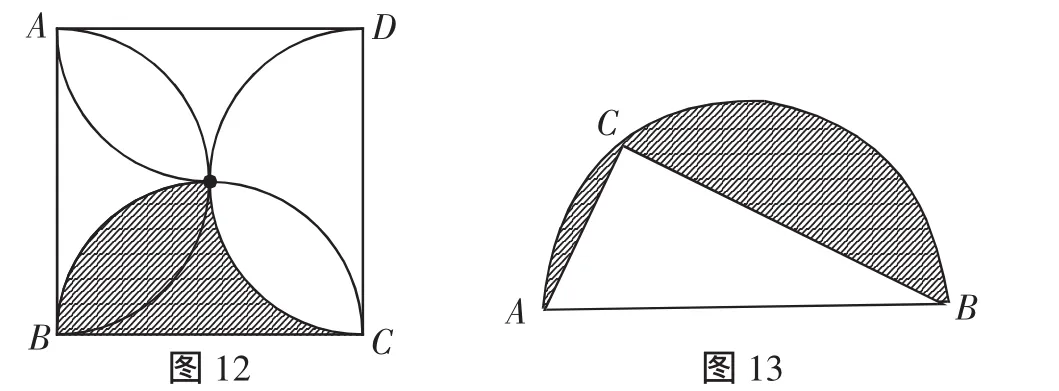
2.如图13,△ABC中,∠C=90°,AC=6,BC=8,以AB为直径在△ABC的同侧作半圆,求图中阴影部分的面积.
3.如图14,已知菱形ABCD的两条对角线长分别为12、16,分别以每边为直径向形内作半圆,求四个半圆弧所围成的花瓣形的面积.
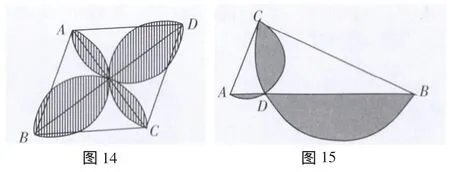
4.如图15,在Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,求图中阴影部分的面积.
5.如图16,正方形的边长为a,分别以两个对角顶点为圆心、以a为半径画弧,求图中阴影部分的面积.
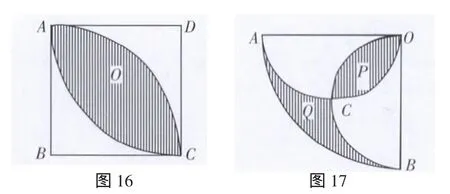
6.如图17,扇形的圆心角为90°,且半径为a,分别以OA、OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是____________.
