基于行波波头瞬时频率的输电线路故障无通道全线速动行波保护

田 智，秦小安，曾祥君

（1.国家电网武汉供电公司，湖北 武汉 430000；2.长沙理工大学 智能电网运行与控制湖南省重点实验室，湖南 长沙 410004）

随着电力系统不断扩大规模、提升电压等级和用户对电网安全性要求越来越高，快速切除故障已成为提高系统暂态稳定性、线路传输能力的重要措施。行波保护因动作速度快，且不易受故障类型、过渡电阻、电流互感器饱和、系统振荡、长线分布电容［1-2］等诸多因素的影响，而受到人们越来载多的重视。行波保护根据需要通信与否可以分为无通道和有通道2种保护。无通道保护不需要两端信息的交换，其可靠性不依赖于通信装置，且动作速度快，因而成为研究的热点。英国Bath大学的A.T.Johns、Z.Q.Bo等在20世纪90年代提出了一系列暂态量无通道保护原理［3］，能准确区分背侧和前方故障，但不能区分线路末端、末端母线及末端母线出口故障。文献［4］提出在线路两端装设调谐电路，通过能否检测到特定频带f的信号来判断区内外故障，但这一原理需要增加一次设备的投入，而且这一方法的灵敏度和它使用的消噪方法存在矛盾。文献［5］考虑了阻波器对行波的阻波作用，提出了一种利用小波变换识别行波陡度来区分区内外故障实现无通道全线速动的行波保护，但利用小波变换时，小波基函数难以选择，而且各尺度受采样频率影响很大。

笔者利用阻波器和母线杂散电容对初始行波波头频率的影响，研究一种无通道行波保护。利用HHT变换提取故障初始行波信号的突变点频率，即故障行波波头瞬时频率，并利用保护区内外故障行波突变点频率高低的不同来实现无通道行波保护。分析和仿真结果表明，该方法简单有效。

1 希尔波特-黄变换

希尔伯特-黄变换（Hilbert-Huang Transform，HHT）是近年来应用于非平稳信号分析的一种新方法［6-7］，它分为两部分：经验模态分解（Empirical Mode Decomposition，EMD）和Hilbert变换。首先利用EMD方法把待分析的信号函数自适应分解，得到有限个瞬时频率有意义的固有模态函数（Intrinsic Mode Function，IMF）［8］。每一个IMF分量所包含的频率成分随信号本身变化而变化，因此，HHT是自适应的信号处理方法，非常适合对非线性和非平稳过程的分析。

1.1 EMD分解

EMD的作用是将待分析的信号分解成有限个IMF，使Hilbert变换的瞬时频率具有实际物理意义。IMF要满足2个条件［8］：①极值点和过零点数目相等或最多差1；②在任意点，由局部极大值和局部极小值形成的两包络的均值为0。EMD是一种经验筛分法，它将复杂信号S（t）从高频到低频依次分解得到有序排列的多阶IMF分量ci（t），最后得到单调的趋势分量rn（t），得到的经验模态分解树如图1所示。第1个IMF分量c1（t）代表原始信号的最高频率成分，非常适合故障行波波头的检测。

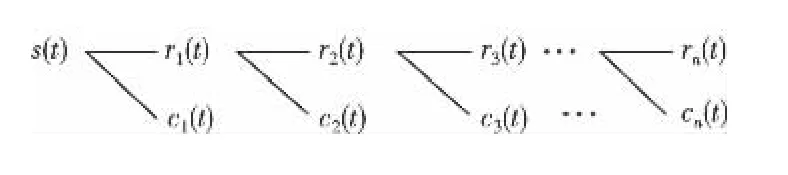
图1 经验模态分解树Figure 1 The tree of empirical mode decomposition

1.2 瞬时频率与Hilbert变换

在平稳信号分析中，频率是Fourier变换的参数，与时间无关。在暂态与非平稳信号分析中，频率必须是时间的函数，不再适合采用Fourier变换进行分析，需引入瞬时频率的概念［8］。

设X（t）为一时间函数，Y（t）是它的Hilbert变换（HT），即

其反变换为

得到解析信号

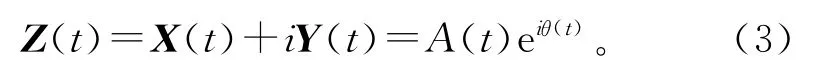
式中 A（t）为 瞬 时 幅 值，A（t）=［X（t）2+为相位

瞬时频率可定义为

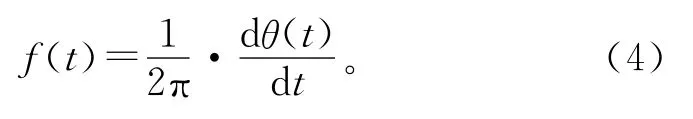
即解析信号Z（t）的相位的导数。式（4）物理意义：解析信号Z（t）表示复平面的一个向量，瞬时频率则表示该向量幅角的转速。

2 保护基本原理

2.1 母线杂散电容对行波波头的影响

当发生故障时，可等效为故障点突然增加一电压源，该电压源产生初始电压行波u0，同时产生初始电流行波i0，设线路的波阻抗为Zc，则i0=u0／Zc，如图2所示。

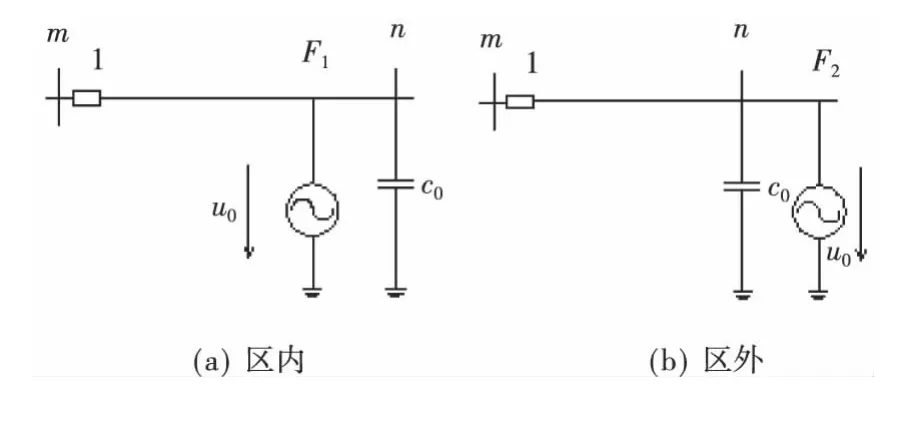
图2 母线杂散电容导致区内、外故障暂态电流的差异Figure 2 The transient current differences between internal and external fault caused by bus-bar capacitance

不计及母线杂散电容时，故障点产生的初始电压行波可以看作是阶跃函数，即

式中 U0为故障瞬间在故障点附加电源的电压幅值。因此，在保护1检测到的初始电流行波为

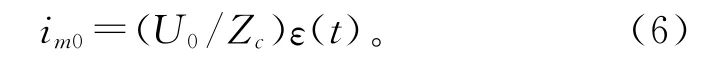
计及母线杂散电容时，设母线杂散电容为Cs，由于杂散电容的影响，在保护1检测到的初始电流行波为

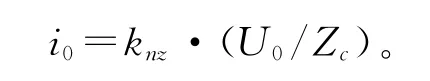
式中 knz为n处的透射系数，knz=Ce-Ct，常数C=2／（ZcCs），因此

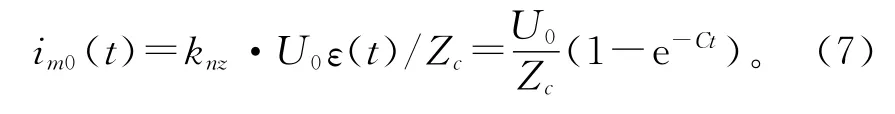
通过比较式（6）、（7）可以发现，不计及母线杂散电容时，保护1检测到的初始电流行波波头具有阶跃性质的陡度；计及母线杂散电容时，保护1检测到的初始电流行波波头陡度变缓，Cs越大，陡度越缓。从频率的观点来看，不计及母线杂散电容时，检测到的初始行波波头频率很高，而计及母线杂散电容时，检测到的初始行波波头频率随母线杂散电容Cs的增大而降低。

2.2 阻波器对行波的影响

中国220kV以上电力线路大多都装有电力线载波设备，包括线路阻波器、藕合电容器、结合设备等。阻波器串联在输电线载波信号点与相邻系统元件（如母线、变压器等）之间，是构成高频保护和载波通信的信号传输通道的重要设备，可阻止高频信号向不需要的方向传送，抑止变电站对载波系统的分流影响，同时可正常地输送工频电流［9］。

现以国产宽带阻波器XZK-1为例（图3）来说明阻波器对行波波头的影响。

图3 行波通过阻波器Figure 3 Travelling wave passes through line trap

当外部故障时，故障行波需经过阻波器到达检测点，所以实际检测到的波头的高频部分被阻波器阻断，而内部故障时，行波波头的高频信号依然存在。因此，当线路内部故障时，由故障点向线路两端传输的行波波头频率非常高；而外部故障时波头频率降低。利用区内外故障行波波头的这一差异就可以构造判据以实现无通道全线速动保护。

2.3 采样频率对仿真实验的影响

目前，通常多数仿真实验都是在确定的采样频率下进行的，依据Nyquist采样定理，采样频率至少为信号最高频率的2倍。但采样频率的不同对仿真得到的信号频率存在影响，一般而言，采样频率越高，采样点数就越密，所得离散信号就越逼近于原信号。因此，采样频率应尽可能高，该文采样频率为10MHZ，远大于研究信号最高频率的2倍，可以满足仿真实验的要求。

3 动作判据

通过分析可知，输电线路区内故障时，检测到的行波信号陡度很大，行波波头频率很高；而区外故障时，由于母线杂散电容和阻波器的影响，检测到的行波信号陡度变缓，行波波头频率降低。主要原因是阻波器阻止高频信号通过阻波器流出故障线路［10］，使得在故障线路检测的行波信号中含有阻波器阻波频段的信号，而在其他线路检测到的行波信号中只含有频率小于下截止频率的信号；另一方面，母线杂散电容也使检测到的初始行波波头频率降低。设阻波器的下截止频率为fc，检测到的行波波头最高频率为f，由公式［9］计算：

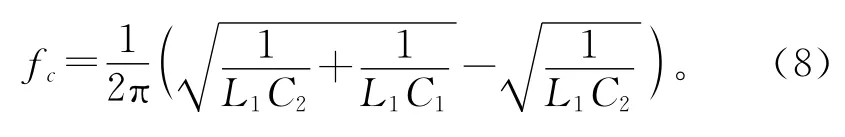
则保护动作判据可描述为

当k＞1时，为区内故障，保护动作，当k≤1时，为区外故障，保护不动作。

动作判据的实现过程：

1）在阻波器首端（线路侧）提取电流行波信号；

2）将电流行波信号通过低通滤波器，将阻波器的上截止频率设置为低通滤波器的截止频率，以滤除电流行波中频率高于阻波器上截止频率的信号；

3）将故障行波信号经过EMD分解，取第1个IMF分量为c1（t）；

4）对c1（t）进行Hilbert变换得到HT（C1·（t）），令得到解析信号为Z（t）=C1（t）+iHT（C1·（t））=A（t）eiθ（t）；

5）对Z（t）求瞬时频率，得到故障行波波头频率f；

6）按式（9）求得k，区分故障。

4 仿真实例

笔者用电磁暂态程序（ATP）对如图4所示的电网系统进行仿真。线路模型全部采用考虑频变影响的分布参数模型（J.Marti模型），线路采用国产500kV宽带阻波器XZK-1，下截止频率为84kHz，阻波频段为84～500kHz，母线电容为0.01μF。仿真试验针对线路MN，采样频率为10MHz。

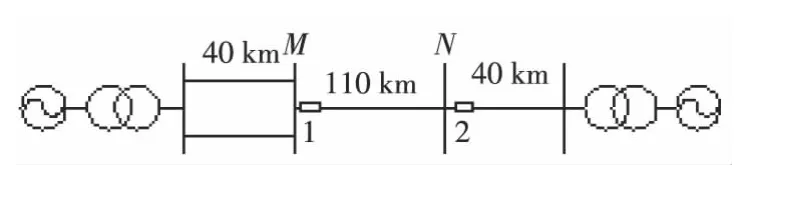
图4 系统结构示意Figure 4 Power system configuration

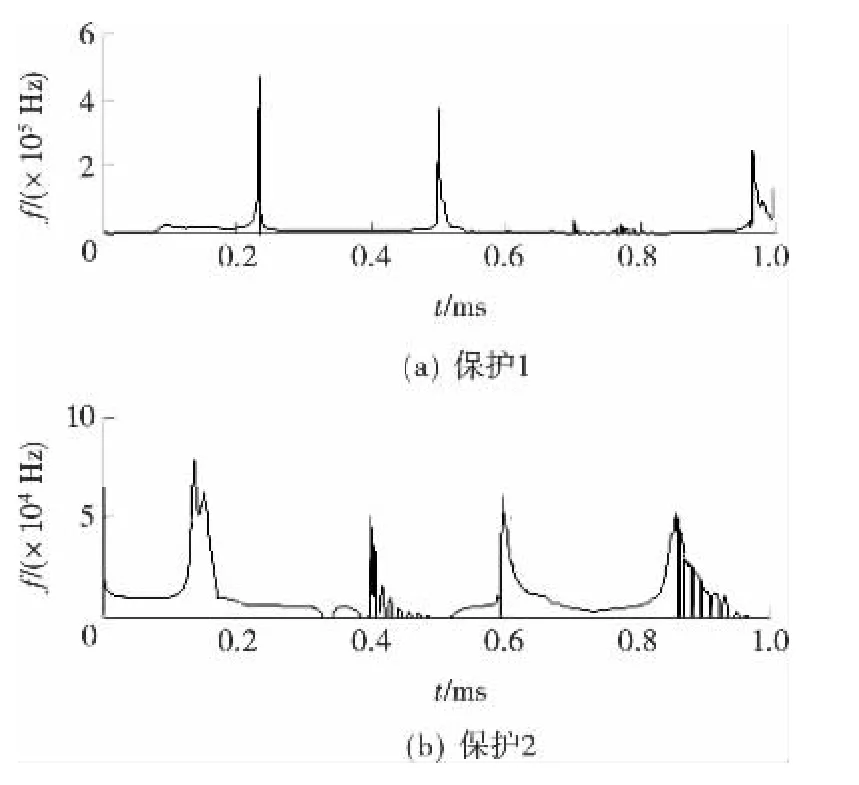
图5 保护1，2检测到的电流行波经过HHT变换的时频Figure 5 HHT time-frequency figure of traveling wave detected at protection 1and protection 2

图5为线路MN距M 70km处故障时，保护1，2检测到的电流行波经过HHT变换得到的时频图，它们的最大频率分别是449.9，75.523kHz，k分别为5.356，0.899。可以看出，对于保护1，频率最大值大于下截止频率，为内部故障；对于保护2，频率最大值小于下截止频率，为外部故障。

4.1 故障类型对保护判据的影响

故障角度为90°、故障电阻为0Ω时，不同地点、不同故障类型情况下的仿真结果如表1所示，表1的数据表明不同的故障类型并不影响保护判据，内部故障时k总大于1，而外部故障时k总小于1。

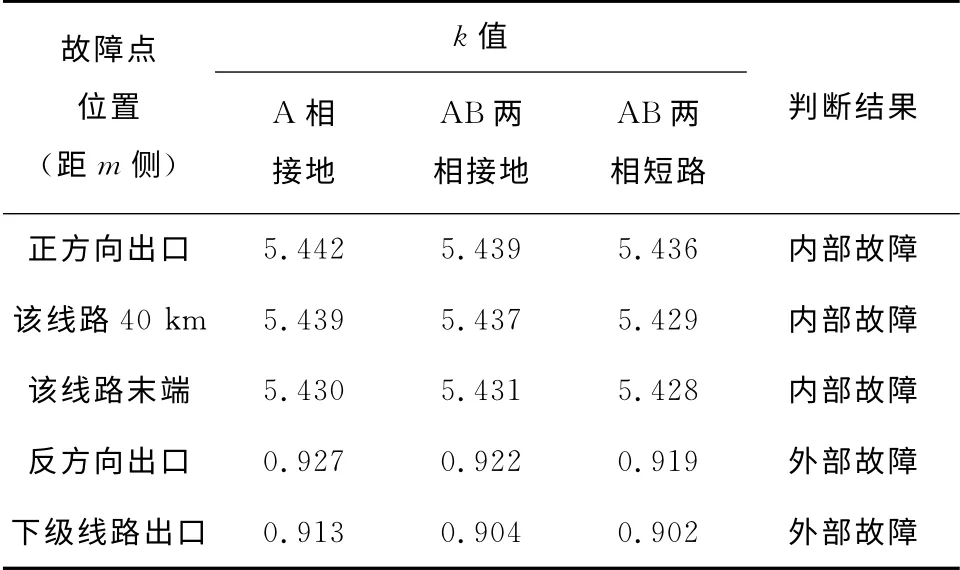
表1 不同类型故障的k值Table 1 Kvalues for different kinds of faults

4.2 故障角度对保护判据的影响

故障电阻为0，单相接地时，不同地点、不同故障初始角的仿真结果如表2所示，可以看出，该保护基本不受故障初始角的影响，只要故障角度不为0，保护都可以正确动作。

表2 故障角度不同的k值Table 2 Kvalue for faults with different phase angles

4.3 故障电阻对保护判据的影响

在不同接地电阻情况下，各故障点发生单相接地故障、故障角度为90°时的仿真结果如表3所示，同样可以看出，接地电阻的存在和大小也不会影响该保护的动作情况。

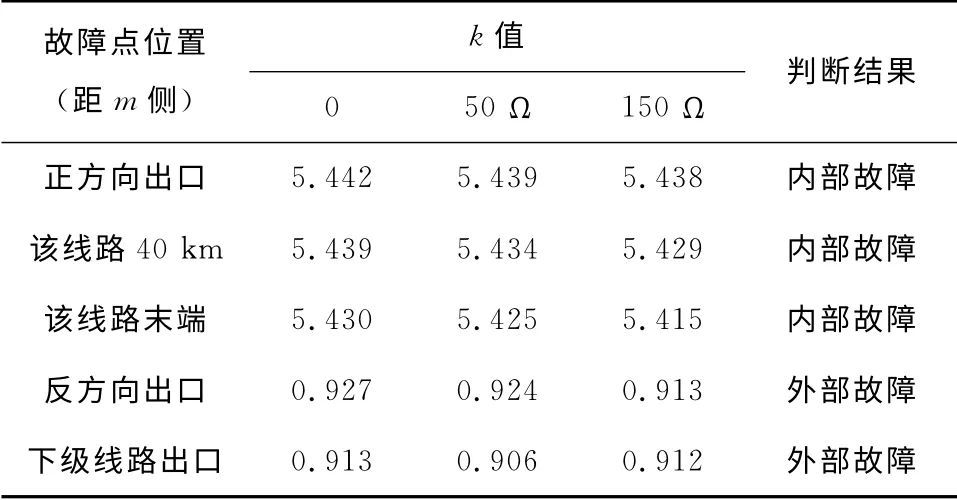
表3 不同接地电阻的k值Table 3 Kvalues for faults with differern grounding resistances

4.4 开关操作对保护判据的影响

不同地点开关操作时，保护的动作情况如表4所示，虽然开关操作产生的电弧中包含大量的高频分量，但它们要经过阻波器才能到达保护检测点，因此，保护判据仍可以正确区分开关操作，表中数据也验证了这一点。

表4 开关操作的影响Table 4 Influence of switching operation

由于该无通道行波保护实际利用的仅仅是初始行波波头信号的频率，因而动作速度非常地快。而且，它不受故障类型、接地电阻和故障角度的影响，实际仿真也证明了这一点。

5 结语

笔者利用基于行波波头瞬时频率的无通道全线速动保护原理，通过分析和仿真，得到结论：

1）该方法不需要通道，可以正确区分各种区内故障和区外故障，可以保护线路的全长；

2）保护只利用了故障点初始行波的频率，数据采集量不大，保护速度快；

3）该方法不受故障类型、故障角度和故障接地电阻的影响，且可以区分开关操作；

4）HHT是分析故障行波信号的一种有效方法。

［1］葛耀中.新型继电保护与故障测距原理与技术［M］.西安：西安交通大学出版社，2007.

［2］周会峰，曾祥君，邓丰.输电线路故障行波网络定位新方法［J］.电力系统自动化，2013，37（19）：93-98.ZHOU Hui-feng，ZENG Xiang-jun，DENG Feng.A new network-based algorithm for transmission line fault location with traveling-wave［J］.Automation of Electric Power Systems，2013，37（19）：93-98.

［3］Bo Z Q.A new non-communrcauon protection technique for transmission lines［J］.IEEE Transations on Power Delivery，1998，13（4）：1 073-1 078.

［4］Aggarwal R K.Theoretical concept and digital simulation of the pramod scheme for UHS protection of EHV transmission lines［J］.IEEE Transations on Power Delivery，1992，7（3）：1 104-1 111.

［5］董杏丽，葛耀中，董新洲.基于小波变换的无通道全线速动行波保护［J］.电力系统自动化，2001，25（10）：18-22.DONG Xing-li，GE Yao-zhong，DONG Xin-zhou.A wavelet andtraveling-wave based non-communication high speed transmission line protection［J］.Automation of Electric Power Systems，2001，25（10）：18-22.

［6］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［C］.Proceedings of the Royal Society of London，London，1998.

［7］赵臻峰，曾祥君，秦小安.基于希尔伯特-黄变换的超高压输电线路行波差动保护［J］.中国电力，2011，44（2）：10-13.ZHAO Zheng-feng，ZENG Xiang-jun，QIN Xiao-an.HHT based traveling wave differential protection used on EHV transmission line［J］.Electric Power，2011，44（2）：10-13.

［8］张小丽，曾祥君，马洪江，等.基于希尔波特-黄变换的电网故障行波定位方法［J］.电力系统自动化，2008，32（8）：64-68.ZHANG Xiao-li，ZENG Xiang-jun，MA Hong-jiang，et al.Power grid faults location with traveling wave based on Hilbert-Huang transform［J］.Automation of Electric Power Systems，2008，32（8）：64-68.

［9］董彦军.高频通道阻波器的特性分析与检测方法研究［D］.北京：华北电力大学，2005.

［10］张仁永，陈宇辉.电力载波通道设备应用指南［M］.北京：中国电力出版社，2002.