Q235的L截面型钢压弯的有限元分析及回弹预测

王大勇，时阳，黄永红

(1.大连交通大学材料科学与工程学院，辽宁大连116028;2.中国北车集团大连机车车辆有限公司工艺部，辽宁大连116028)*

Q235的L截面型钢压弯的有限元分析及回弹预测

王大勇1，时阳1，黄永红2

(1.大连交通大学材料科学与工程学院，辽宁大连116028;2.中国北车集团大连机车车辆有限公司工艺部，辽宁大连116028)*

分析发电机风道前托架的弯曲工艺，引入相对弯曲半径系数C，对传统板材压弯回弹预测公式进行修正，得到计算L截面型钢回弹的公式.利用有限元软件DYNAFORM对Q235材料的L截面型钢压弯模拟，对回弹进行预测，结合试验反推出C值，总结出C值和相对弯曲半径r0/H关系曲线.利用该曲线可以计算出所需的凸模圆角半径值，优化了模具设计和压弯工艺，为实际生产中的压弯模的设计提供参考，减少了试模次数，降低生产成本.

回弹;压弯L截面型钢;有限元;相对弯曲半径系数C

0 引言

回弹是板材冲压成形过程中产生的一种缺陷，回弹的存在是不可避免的，影响回弹的因素多种多样，关于回弹问题人们也做了大量工作，主要是通过对回弹的预测和控制两方面进行研究，首先是对回弹进行预测，方法主要包括理论解析法，数值模拟法，实验法，然后通过改善成形工艺和模具补偿法来实现对加工零件回弹的控制，近年来，板材回弹的研究逐渐成熟［1－7］.

回弹缺陷同样影响着型材的加工成形，但相对于板材型材回弹预测缺少准确的数据做指导，传统的冲压手册中关于回弹的经验公式及模具设计数据也主要针对平面板材，应用于型材有很大的误差，使得型材弯曲模具设计费时费力，严重影响生产效率.压弯成形作为一种经济，高效的加工方法在实际的生产中得到普遍应用，但是其精度较低，而且关于型材压弯回弹的资料数量更是有限.因此，参考板材回弹研究方法对型材压弯法进行回弹研究对实际生产具有一定的指导意义.

1 工艺及理论分析

图1所示为机车上使用的一个构件—发电机风道前托架，由材料为Q235的L截面型材通过压弯成形.从尺寸上看零件的弯曲半径较大，很难进行一次性压弯得到，必须通过多道压弯才能实现成形.

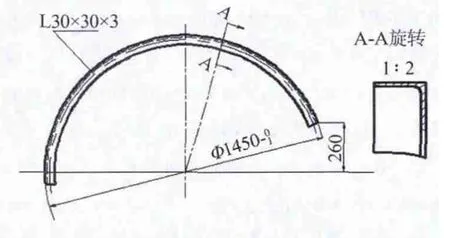
图1 零件尺寸

根据板材的回弹预测公式［8］:

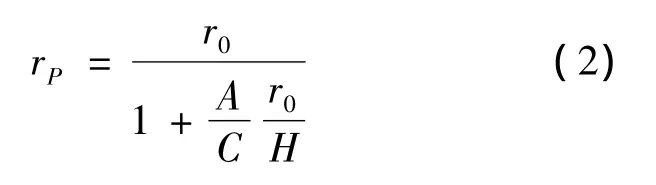
式中，rp为凸模圆角半径(mm);r0为工件回弹后的半径(mm);A为材料的弹性模量简化系数(A=3σs/E);C为相对弯曲半径系数;H为型材翼板的高度(mm).

将式(2)作为预测L截面型钢回弹的公式，确定C值的大小是要解决的主要问题，需要通过对具有不同的相对弯曲半径r0/H的L截面型材进行试验得到，试验时多次试模和修模工作量和费用巨大，因此，需要借助有限元模拟软件的辅助.

2 模拟分析

2.1 建立有限元模型

随着计算机技术的快速发展数值模拟法被越来越多的应用于解决塑性成形问题，其中DYNAFORM软件在分析板材的回弹问题方面被广泛的使用，通过数值模拟的方法对公式进行检验首先，建立有限元模型并划分网格如图2所示.单元类型采用BT壳单元，抽取坯料中性层来作为模型.划分模具和坯料的最小网格尺寸均为为0.5 mm，最大为5 mm.设置凸模运行速度为300 mm/s.利用动力显式算法计算压弯过程，再通过静力隐式计算卸载后的回弹.将每一步完成回弹计算坯料的文件(后缀名为dynain)重新导入到DYNAFORM前处理中，调整坯料与模具的相对位置，再进行下一道压弯和回弹计算［9］.这样做的目的是由于前一道工序的模拟结果直接影响下一道工序的模拟精度.通常在模拟板料的多步冲压过程时，都忽略了每道工序后板料的回弹，即忽略了板料在每道工序后的应力变化，而板料的回弹计算精度又与其变形历史密切相关［10］.在多步冲压模拟中间加进回弹计算，相对传统的多步冲压模拟过程而然，避免了因忽略每道工序后的回弹而造成的应力变化模拟不正确，进而影响最终回弹精度［11］.成形计算过程采用全积分单元，厚度方向5个积分点，LS－DYNA中提供了12种迭代方法，其中BFGS法是缺省方法，这是目前最成功的一个变尺度算法，是一种拟牛顿法，收敛速度快，且具有较好的数值稳定性.隐式参数的设置对回弹精度和收敛有重要影响［12-13］.对于初步设计方案，进行每一道压弯时坯料的送进量为1倍的凸模宽度，发现在翼板上存在一定的起皱现象，如果减小送料量会改善这种现象，并调整凸模和挡板的间隙为1.1倍的板厚，经过多次模拟将每次的送料量确定为2/3倍的凸模宽度，修改后的模型如图3所示，修改模型后既改善了翼板起皱现象又保证了给料量不至于影响效率，如图4所示.

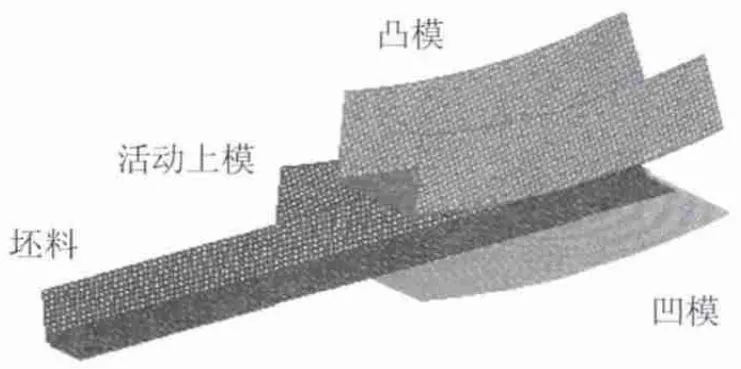
图2 有限元模型的建立及网划分

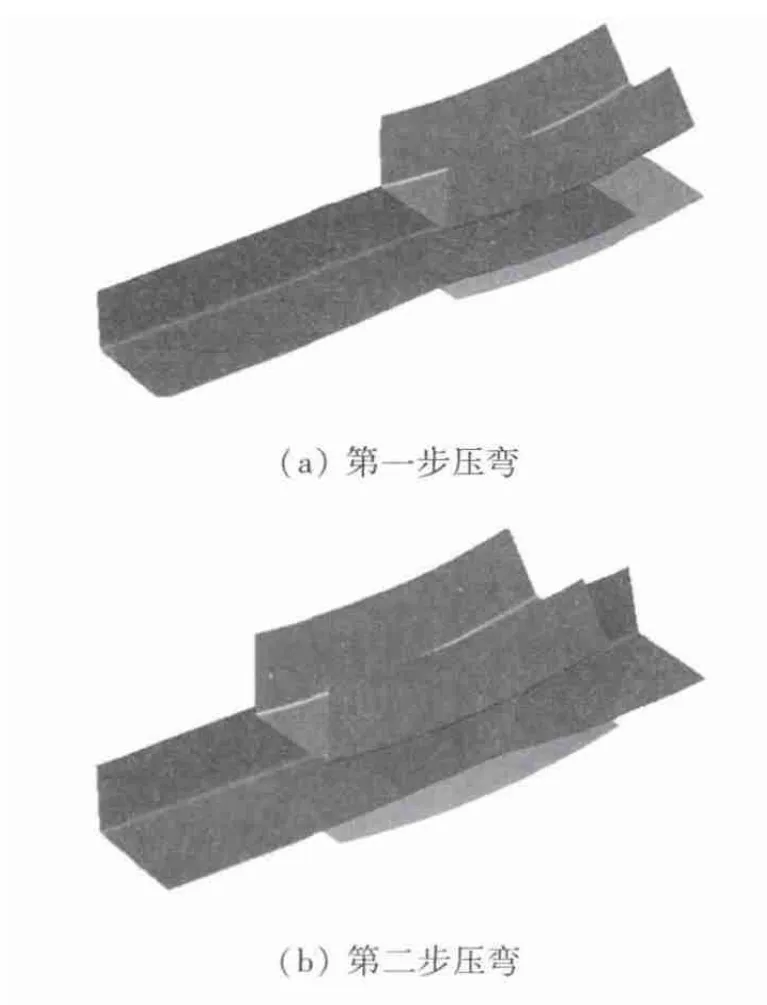
图3 调整坯料给料量后的模型

图4 两种方案下的起皱现象分析图

对截面30 mm×30 mm，材料为Q235的L截面型钢，在不同的相对弯曲半径r0/H情况下进行模拟压弯，并结合试验测量其回弹后的半径值r0，再计算回弹半径Δr=r0－rP，最终得到相对弯曲半径r0/H与回弹半径Δr的关系如图5所示.模拟结果和试验结果得到较好的吻合，验证了模拟的可靠性.

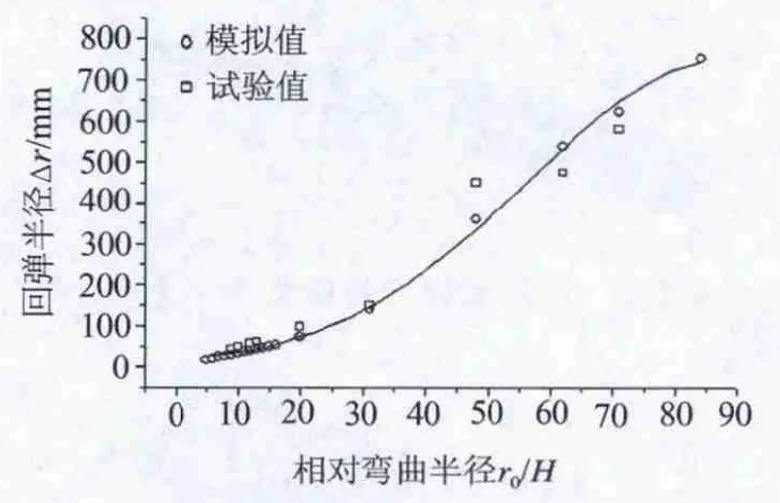
图5 相对弯曲半径r0/H和回弹半径Δr的关系

图5 相对弯曲半径r0/H与相对弯曲半径系数C的关系

2.2 试验验证

对图1所示的发电机风道前托架进行回弹的预测，相对弯曲半径r0/H=725/30≈24，弹性模量简化系数A=0.005，由图5可以查得相对弯曲半径系数C≈0.7，根据式(2)设计凸模圆角半径rp≈619 mm，实际设计凸模圆角半径为640 mm，与实际吻合的较好.

3 结论

(1)借助有限元模拟软件DYNAFORM可以对回弹进行预测，并可以预先知道模具设计的不足;

(2)模拟软件的参数设置的合理性直接影响模拟结果的准确性，需要结合一定的试验来对预测精度加以保证;

(3)将板材回弹预测公式中的板厚t换成翼板高度H，并引入相对弯曲半径系数C值，修改后的公式可以比较准确的预测L截面型钢压弯回弹值，为实际生产中凸模的设计提供参考，减少试模次数，降低成本.

［1］刘桂花，冯再新，贾青云，等.板料冲压成形过程中回弹预测及控制的研究进展［J］.金属铸锻焊技术，2011(17):122-125.

［2］余同希，章亮炽.塑性弯曲理论及其应用［M］.北京:科学出版社，1992.

［3］HILL R.The Mathematical Theory of Plasticity［M］.London:［s.n.］，1950.

［4］JOHNSON W，YU T X.Springback after the biaxial elastic-plastic pure bending of a rectangular plate-I［J］.International journal of mechanical sciences，1981，23:619-630.

［5］JOHNSON W，YU T X.On the range of applicability of results for the springback of an elastic－perfectly plastic rectangular plate after subjecting it to biaxial pure bending II［J］.International journal of mechanical sciences，1981，23:631-637.

［6］林忠钦，刘罡，李淑慧，等.应用正交试验设计提高U型件的成形精度［J］.机械工程学报，2002，38:83-89.

［7］杨雪春，董懿琼，彭伟，等.U型件回弹控制模具补偿法的研究［J］.锻压技术，2009，2(1):48-52.

［8］杨玉英，崔令江.实用冲压工艺及模具设计手册［M］.北京:机械工业出版社，2005.

［9］陈文亮.板料成型CAE分析教程［M］.北京:机械工业出版社，2005.

［10］徐丙坤，施法中.板料冲压成形回弹的数值模拟［J］.北京航空航天大学学报，2001(2):194-197.

［11］陈炜，王晓路，高霖.板料多步冲压回弹的数值模拟研究［J］.塑性工程学报，2005(5):12-15.

［12］龚红英.板料冲压成形CAE实用教程［M］.北京:化学工业出版社，2009.

［13］BRADLEY N，MAKER，XINHAI ZHU.Input Parameters for Metal Forming Simulation using LS-DYNA［M］.Livermore:Software Technology Corporation，2000:1-10.

FEA and Prediction Study of Q235 L-Section Steel in Press Bending Springback Process

WANG Da-yong1，SHI Yang1，HUANG Yong-hong2

(1.School of Materical Science Engineering，Dalian Jiaotong University，Dalian 116028，China;2.Dalian Locomotive and Rolling Stock Co.，Ltd，CNR Group，Dalian 116022，China)

Bending process of generator air duct bracket was analysed，and the relative bending radius coefficient C was introduced to revise the traditional plate bending springback prediction formula to obtain springback prediction formula of L-section steel.The bending process of the L-section steel was simulated by DYNAFORM，and the springback was predicted.Value C was

by experiment，and the relationship between value C and relative bending radiusr0/Hwas summed up.The die radius needed can be obtained by the relation curve，then the design of the die and the bending craft was optimized，which is reference to the die design to reduce the experiment and the production cost.

springback;press bending L-section;FEA;relative bending radius coefficient C

A

式中，rp为凸模圆角半径;r0为板材回弹后的半*

2013-03-28

10.13291/j.cnki.djdxac.2014.03.021

1673-9590(2014)03-0088-04

王大勇(1971－)，男，副教授，学士，主要从事金属塑性成形技术的研究

E-mail:wangdy@djtu.edu.cn.径;σS/E为屈服强度和弹性模量的比值;t为板材厚度，而对于同种材料，L截面型钢相对于等厚的板材只增加了一个高度为H的翼板，翼板对回弹起到限制的作用，板厚的作用不如翼板，所以，假设将式(1)中的t换成H，型材的相对弯曲半径为r0/H，并且引入相对弯曲半径系数C，因此将式(1)修改为