TRMM降水数据在复杂山地的精度评估
——以重庆市为例
2014-01-26吴建峰陈阿林鲁小平
吴建峰,陈阿林,嵇 涛,李 军,鲁小平
降水是参与全球水和能量循环过程中关键要素之一,准确掌握降水信息对研究大气循环和水循环过程起着至关重要的作用。空间化的降水信息对于区域水资源分析,水文以及区域水资源管理,生态环境治理,旱涝灾害管理等具有重要的意义[1]。传统区域降水量的估算数据通常来自地面气象站点的观测,但由于受气象站点位置、站网密度等限制,不能准确把握降水的空间分布和强度变化,进而不能满足研究和应用需要[2]。相比之下,基于卫星的降水观测数据具有不受地形和气候条件限制、覆盖范围广、时空分辨率高等优势,已成为降水数据的重要来源[3]。TRMM(tropical rainfall measurement mission)降水数据是由美国NASA和日本NASDA(national space development agency)共同研制开发。可向全球提供50°N—50°S间的降水数据。TRMM降水至今已获取了海量的高时空分辨率降水数据,为与降水相关的研究提供了新的数据支撑[4]。目前,TRMM降水数据已经得到较广泛的应用,如利用TRMM星载PR和TMI数据分析降水空间分布和季节变化特征[5-6],研究热带气旋的降水分布特征、降水与水汽潜热关系[7-8]等。根据TRMM降水数据研究区域结构特征、降水水平分布特征[9-10],以及作为耦合模型的气象输入,模拟流域的陆面水文过程等[11]。目前,国内外在TRMM降雨的分析和资料验证等方面的研究表明,TRMM数据与气象站点和雷达观测数据具有良好的一致性[12-13]。由于山地区域的降水分布十分复杂,它既与气候条件(经纬度)有关,又受地形(如坡向、坡度、遮蔽度等)、海拔等地形条件的影响[14-16]。但目前的研究多集中在地势较为平坦的区域,对于重庆市这样地势较复杂、地形起伏明显的区域研究还较为匮乏,且研究侧重数据精度的检验,而对数据精度影响因子的分析也较缺乏。因此,本研究以下垫面相对复杂的重庆地区为对象,选取2000—2011年重庆地区34个气象站点降水资料,对同期的TRMM 3B43降水数据在月、季和年3个时间尺度的降水进行精度检验评估,探讨其在重庆地区的适用性,并分析高程和坡度对数据精度的影响,旨在为TRMM降水数据的订正提供科学依据。
1 研究区概况
重庆市位于四川盆地东部,地跨105°17′—110°11′E、28°10′—32°13′N,是青藏高原与长江中下游平原的过渡地带,渝东、渝东南临湖北省和湖南省,渝南接贵州省,渝西、渝北连四川省,渝东北与陕西省和湖北省相连。幅员面积8.24×104km2。气候温和,属于亚热带湿润季风气候,年平均温度在18℃左右,雨热同季,降水充沛但季节分配不均,多年平均降水量介于1 000~1 450mm之间。长江干流自西向东横贯全境,流程长达665km,横穿巫山三个背斜,形成举世闻名的“长江三峡”。地貌形态复杂多样,主要以山地丘陵为主,地势由南北向长江河谷逐级降低,西北部和中部以丘陵、低山为主,东北部靠大巴山和东南部连武陵山两座大山脉。
2 数据来源与研究方法
2.1 数据来源
本文所用的数据包括TRMM 3B43数据(简称TRMM数据)、气象站点实测的降水数据和DEM数据。(1)TRMM 数据可从网站http:∥trmm.gsfc.nasa.gov/免费下载,其时间分辨率为1个月,空间分辨率为0.25×0.25°(约为25km),选取的时段同降水实测数据相同。(2)降水观测数据来自中国气象数据共享服务中心,选取2000—2011年重庆地区34个国家基准与基本站观测数据,对TRMM卫星降水数据进行检验。在研究过程中以气象站点实测数据作为检验值。(3)DEM数据为ASTER GDEM,其空间分辨率为1弧度秒(约30m),数据覆盖范围为83°N—83°S之间的所有陆地区域。
2.2 研究方法
(1)相关系数。用来揭示TRMM 3B43降水数据与站点实测数据之间相关关系的密切程度,参考文献[17]。
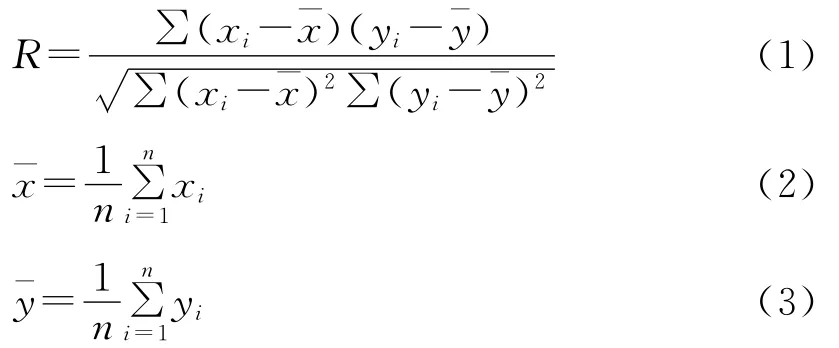
式中:n——样本容量;xi,yi——气象站点实测数据和TRMM降水数据。R取值范围[0,1],越接近于1,数据一致性越好。
(2)相对偏差。是指TRMM卫星数据与站点实测数据之间的偏差,反映两者之间的偏离程度。
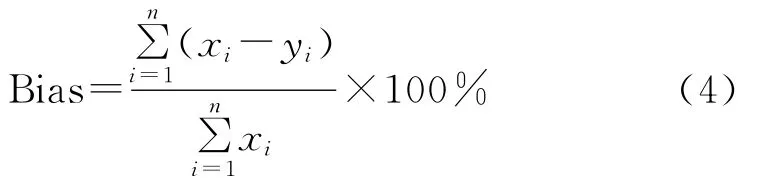
Bias反映了TRMM降水数据与站点实测降水在数值上的偏离程度,Bias越接近0,则说明数据越精确。
(3)采用三次多项式回归和指数函数用于分析高程对TRMM降水数据的影响。三次多项式回归和线性回归用于分析坡度对TRMM降水数据的影响,该分析都是在SPSS 17.0统计软件中实现。
(4)考虑到研究区复杂的地形条件对卫星降水估算造成的影响,分别以高程(elevation)和坡度(slope)为自变量,相关系数(R)、绝对偏差(|Bias|)为因变量进行回归分析,分别得出高程和坡度对相关系数以及绝对偏差的影响,最后采用主成分分析法分析重庆地区高程和坡度对TRMM 3B43降水数据的影响程度。
3 数据精度检验
3.1 年降水量检验
利用TRMM降水数据对重庆所有站点的年降水量进行拟合(图略),拟合结果通过了a=0.01下的置信度检验,具有较好的拟合效果。研究区内34个气象站点的平均年降水量相对偏差为5.86%,TRMM年降水量普遍高于气象站点的实测结果。从研究区的空间分布来看,渝东北(云阳县、巫溪县、奉节县、巫山县、万州区)以及渝中(石柱县、丰都县、武隆县、黔江区、綦江区)的相对偏差较大,最大在石柱地区,达到25.4%;而渝西、渝南等其它区域的相对偏差较小,其中城口的偏差绝对值最小,仅为0.55%。从以上空间分析来看,海拔相对较高的区域的一般相对偏差较大,而海拔相对较低的地方的相对偏差较小。总体而言,TRMM估算的年降水数据精度较高,能够满足在年尺度上应用的需要。
3.2 季降水量检验
季节的不同带来的降雨量也存在差异,特别是在大陆区域这种现象更明显。重庆地区处于中亚热带湿润季风气候区,降水充沛但季节分配不均,夏季降水多于冬季。因此有必要对TRMM降水数据进行各季节精度验证。把整个研究区34个地面气象站点2000—2011年的降水数据按(春季:3—5月;夏季:6—8月;秋季:9—11月;冬季:12—月至翌年2月)进行计算,并与对应同期的TRMM降水数据进行线性拟合,结果如图1所示。秋季的拟合优度最高(R2=0.64),其次为春季(R2=0.50)、夏季(R2=0.48),拟合优度最低的是冬季(R2=0.43)。这也与已有的一些研究结果相符,Ebert等[16]用澳大利亚的雨量计数据对TMPA—RT进行验证的结果显示数据精度检验在相对降雨强度大和暖季的时候表现较好,而在降雨强度小和冷季的时候表现较差。与1∶1对角线对比,夏季的降水大部分位于上半区,表明TRMM估算的降水高于气象站点的降水;冬季的降水多半位于下半区,表明TRMM估算的降水低于气象站点的降水;春季和秋季的降水基本均匀分布与1∶1对角线两侧,即说明TRMM估算的降水与气象站点的降水相当,反映出在春季和秋季TRMM降水的估算比较准确。

图1 研究区2000-2011年TRMM 3B43降水量与地面观测站各季降水量的关系
3.3 月降水量检验
以2000—2011年研究区34个气象站实测月降水量为自变量,以对应月份各气象站点所在的格网内TRMM月降水数据为因变量进行线性回归分析(图2)。由图2可知,TRMM月降水数据与站点实测降水量的拟合优度R2=0.73,相关系数为R=0.85,并通过置信度100%检验,说明TRMM降水数据与站点观测数据之间具有明显的线性相关性。

图2 研究区2000-2011年TRMM 3B43降水与地面观测月降水量的关系
3.4 单个站点数据精度检验
以上从年、季度和月这3个不同尺度下检验结果分析可知,整体上TRMM月降水数据与站点实测降水量之间存在很好的相关性,数据精度较高。但从整体上进行检验难免会掩盖某些站点数据与对应TRMM降水数据之间的差异,而无法全面客观地反映出TRMM月降水数据在各实测站点数据间精度的差异性,尤其因为降水是所有气象要素中最活跃的变量,其分布受到地形、气候、经纬度、海拔、海陆位置等诸多因素的影响,具有时间上和空间上的高度不连续性与非线性特征[17]。因此,仅对数据进行整体精度检验不够全面,还需要对单个站点进行精度检验。
以研究区34个气象观测站点2000—2011年的实测月降水量为自变量,相应时间上站点所在格网内的TRMM月降水数据为因变量进行线性回归分析,得到TRMM月降水数据与各站点实测降水量之间的相关系数(表1)。从34个气象站点中选取16个气象站进行散点分析,站点的选择主要考虑空间分布相对均匀和代表地形特征两方面因素[18],散点图由于篇幅有限,此处图略。
由表1相关系数得到:(1)大部分TRMM降水与气象站点数据之间具有很好的相关性,相关系数都大于0.80。该结论与数据精度整体验证的结论相一致,进一步表明了在重庆地区TRMM月降水数据与站点实测降水量存在明显的线性关系,遥感数据精度较高,具有普遍实用性。(2)各气象站实测降水与TRMM降水数据的相关系数分布不均匀,其中相关系数最高的为城口站(R=0.94),丰都站相关系数最低(R=0.80)。说明城口站点实测的降水与TRMM月降水之间的相关性较高,而丰都站相关性相对较弱,这与站点的局部位置和地形有密切的关系。丰都地形起伏明显,海拔为118~2 000m,但该站点的高程为290.5m,这就造成了站点实测的降水数据不能全面代表站点周围的降水状况。
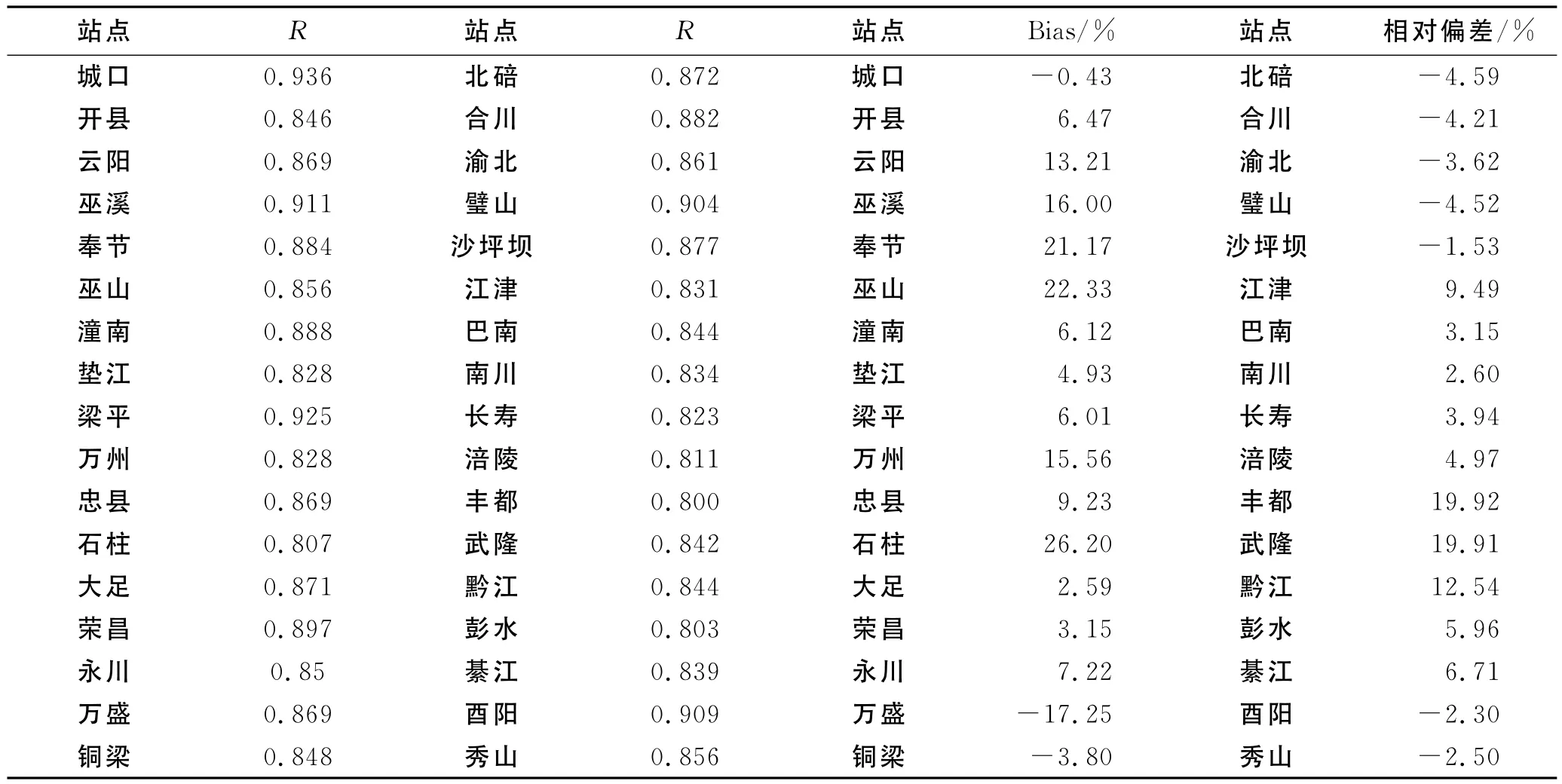
表1 基于月降水量2000-2011年TRMM 3B43数据与站点实测值相关系数和相对偏差
通过相关系数可以反映出TRMM月降水数据和站点实测降水量之间相关性大小,却不能客观反映两者之间的数值差异程度,因此对两者进行相对偏差的研究,从而客观地反映TRMM月降水数据和站点实测降水量之间数字差异大小。本文利用公式(2)进行各站点相对偏差的计算,结果详见表1。
由表1中相对偏差数据分析可知:(1)在34个气象观测站点中,城口、万盛、铜梁、北碚等10个站点的相对偏差为负,表明TRMM月降水数据相比于站点实测降水量存在低估;开县、巫溪、垫江、綦江等24个站点的相对偏差为正,表明TRMM月降水数据相比于站点实测降水量存在高估。(2)在34个气象观测站点中,有城口、垫江、大足、秀山等24个站点的相对偏差在[-10%,10%]范围内,表明整体上TRMM月降水数据跟站点实测降水量在数值上差异不大,在一定程度上能够反映出TRMM降水数据的准确性。可能是由于这些站点的高程与所在区域的平均海拔差异不大,站点实测数据能真实地反映降水。(3)研究区内各气象站点的相对偏差存在着不同程度上的差异,其中城口、大足、沙坪坝、南川、酉阳、秀山6个气象站点的相对偏差的绝对值小于3%,显示了TRMM月降水数据和站点实测降水量具有很好的一致性。而奉节、巫山、石柱相对偏差分别为21.17%,22.33%和26.20%,表明这3个站点TRMM月降水数据和站点实测降水量存在较大的偏差,这3个站点对应的相关系数R都较高,分别为0.89,0.86和0.81,这也论证了仅从相关系数来考虑TRMM月降水数据和站点实测降水之间的相关性,容易忽略相关系数较高的降水数据之间可能存在较大偏差,因而分析两者之间的相对偏差是有必要的。
通过以上精度检验分析结果可得出,整体上来看,TRMM月降水数据与站点实测降水之间具有很好的一致性。所有站点的平均相关系数达0.86,丰都站相对其它站点较低(R=0.80)。在34个气象观测站点中,城口、垫江、大足、秀山等24个站点的相对偏差在[-10%,10%]范围内,表明大多数站点TRMM月降水数据与站点实测降水量差异不大。
4 高程和坡度对TRMM 3B43数据的影响
重庆市地处四川盆地东部,属我国地势第二级阶梯,主要地貌类型包括中山、低山、丘陵、台地、平原等,高程落差较大,考虑到降水在一定程度上受到地形因素的影响,因此从高程、坡度两个地形因子对TRMM数据精度的关系进行分析。
4.1 高程对TRMM 3B43降水数据的影响
从重庆地势分布来看,东北部有大巴山地,东南部斜贯有巫山、大娄山等山脉,其西为丘陵,中部主要为低山与丘陵相间排列的平行岭谷类型组合。
以TRMM数据与气象站观测数据之间的相关系数为因变量,以研究区域的气象站点高程为自变量,进行三次多项式回归分析,回归结果详见表2。

表2 重庆地区高程与相关系数的回归模型检验及参数估算值
根据分析结果可得,两者之间具有一定的相关性,相关系数R=0.43,通过了a=0.1条件下的置信度检验,从分析结果趋势图得出(图略),随着海拔的增大,所对应的相关系数呈现出先增大,再略微减小,最后逐渐增大变化趋势。以TRMM数据与气象观测数据的绝对偏差为因变量,以研究区域的气象站点高程为自变量,作指数函数分析,结果详见表3。根据表3可得,虽然两者的相关性不强,相关系数仅为0.33,但通过了a=0.1条件下的置信度检验,从分析结果趋势图看出,二者呈现一种反比特性,随着海拔的增大,所对应的绝对偏差呈现出减小的变化趋势。综上所述,海拔对TRMM数据的精度的影响总体表现为海拔越大,TRMM数据的质量呈现越好的趋势。结果表明:(1)地形对山地降水的影响较大,随海拔升高降水量具有显著的变化规律,这种变化通常不是简单的线性关系[19]。高程和坡度对降水影响十分显著,这些都使得该地区的降水变化十分复杂,造成误差较大最主要因素。(2)气象站点大多布设在山前平原区或低山带,分布相对稀疏且不均匀,因而TRMM降水资料与气象站点观测数据之间存在一定的差异,是产生误差较大的另一重要原因。

表3 重庆地区高程与绝对偏差的回归模型检验及参数估算值
4.2 坡度对TRMM 3B43数据的影响
研究区的坡度呈现出巫山—万盛一线的坡度较大;其西和中部主要为低山与丘陵,坡度较平缓。以TRMM数据与地面气象站点数据之间的相关系数为因变量,以坡度为自变量进行三次多项式回归分析,结果详见表4。由表4可知,两者的相关系数为0.44,通过a=0.1下的置信度检验。两者之间的关系较复杂,呈现出的三次关系特征,随着坡度的升高,相关系数呈现出增加—减少—增加的变化趋势,这跟高程与相关系数的趋势有类似之处。

表4 重庆地区坡度与相关系数的回归模型检验及参数估算值
采用类似方法,以TRMM数据与气象观测数据的绝对偏差为因变量,以坡度为自变量,进行一次线性回归分析,结果如表5。由表5可知,两者的相关系数为0.44,通过a=0.01置信度检验。两者之间存在较明显的线性关系,随着坡度值的升高,绝对偏差|Bias|呈现出逐渐增加的趋势。总体来看,TRMM数据质量在一定程度上受坡度影响。

表5 重庆地区坡度与相关系数、|Bias|的回归模型检验及参数估算值
4.3 主成分分析
为反映高程与坡度对数据质量影响的程度评价,采用相关系数、绝对偏差、高程与坡度来表示TRMM数据的精度,将4个变量进行标准化处理,采用主成分分析方法,得到两个主成份F1和F2,累计贡献率分布为39.26%和72.15%,特征值分别为1.57和1.32,其中:

由主成分分析的贡献率可以看出:高程和坡度对TRMM降水的贡献程度分别为16.59%和11.26%,因此,综合分析可得在重庆地区高程和坡度对数据质量有一定的影响,且高程对数据质量的影响大于坡度。
5 结论
(1)年尺度,整体上TRMM年降水量高于气象站点的实测结果。34个气象站点平均年降水量相对偏差为5.86%,海拔相对较高的渝东北和渝中区域的相对偏差较大;季节尺度,拟合优度较高,TRMM降水数据能够较好的反映季节降水的特征,但各季节也存在一定差异,其中秋季拟合效果高于其它几个季节;TRMM月降水数据与站实测降水量相关系数为R=0.85,通过置信度100%检验,说明TRMM与观测数据之间具有明显的相关性。
(2)对34个气象站点的TRMM月降水数据进行逐个精度验证,整体上来看,所有站点的相关系数都达到0.80,大部分站点的绝对偏差都在10%以内,表明TRMM月降水与站点实测降水具有很好的一致性,其中城口站最好,奉节、巫山、石柱站相对偏差较大。
(3)高程和坡度对降水数据质量的影响呈现出较复杂的态势。随着海拔的升高,相关系数呈现出“增加—减少—增加”的变化趋势,绝对偏差表现为减小的变化趋势。随着坡度值的升高,绝对偏差表现为“增加—减少—增加”的态势,绝对偏差呈现出线性增加的趋势。利用主成分分析方法得到高程和坡度对TRMM降水的贡献程度分别为16.6%和11.3%,表明高程对数据精度的影响大于坡度。
(4)本研究TRMM降水的空间分辨率为0.25°×0.25°,空间分辨率略显粗糙,对于局部小范围的降水观测还达不到站点观测在反映降水随时间变化方面的精度,以后研究方向为:实现降水数据产品高精度重建,提高空间分辨率;将TRMM降水与站点观测数据有效的结合,相互补充,提高水文预报精度。
[1] 朱会义,贾绍凤.降雨信息空间插值的不确定性分析[J].地理科学进展,2004,23(2):34-42.
[2] 杨扬,张建云,戚建国,等.雷达测雨及其在水文中应用的回顾与展望[J].水科学进展,2000,11(1):92-98.
[3] 郝振纯,童凯,张磊磊,等.TRMM降水资料在青藏高原的适用性分析[J].水文,2011,31(5):18-23.
[4] 刘俊峰,陈仁升,韩春坛,等.多卫星遥感降雨数据精度评价[J].水科学进展,2010,21(3):343-348.
[5] 傅云飞 刘国胜.Precipitation characteristics in midlatitude East Asia as observed by TRMM PR and TMI[J].Journal of the Meteorological Society of Japan,2003,81(6):1353-1369.
[6] 陈举,施平,王东晓,等.TRMM卫星降雨雷达观测的南海降雨空间结构和季节变化[J].地球科学进展,2005,20(1):29-35.
[7] 丁伟钰,陈子通.利用TRMM资料分析2002年登陆广东的热带气旋降水分布特征[J].应用气象学报,2004,15(4):436-444.
[8] 牛晓蕾,李万彪,朱元竞.TRMM资料分析热带气旋的降水与水汽、潜热的关系[J].热带气象学报,2006,22(2):113-120.
[9] 傅云飞,宇如聪,崔春光,等.基于热带测雨卫星探测的东亚降水云结构特征的研究[J].暴雨灾害,2007,26(1):9-20.
[10] 刘奇,傅云飞.基于TRMM/TMI的亚洲夏季降水研究[J].中国科学(D辑):地球科学,2007,37(1):111-122.
[11] 杨传国,余钟波,林朝晖,等.基于TRMM卫星雷达降雨的流域陆面水文过程[J].水科学进展,2009,20(4):461-466.
[12] Nazrul I,Hiroshi U.Comparison of TRMM 3B42Prod-ucts with surface rainfall over Bangladesh[J].Hydrological Sciences Journal,2005,48(6):4112-4115.
[13] 骆三,苗峻峰,牛涛,等.TRMM测雨产品3B42与台站资料在中国区域的对比分析[J].气象,2011,37(9):1081-1090.
[14] 傅抱璞.地形和海拔高度对降水的影响[J].地理学报,1992,47(4):302-314.
[15] 任小玢,董治宝,周正朝.近50年来四川盆地降水日数的时空变化特征[J].水土保持通报,2012,32(4):65-70.
[16] Ebert E E,Satellite vs.model rainfall:which one to use?[C]∥Proceedings of the 5th International Scientific Conference on the Global Energy and Water Cycle Costa Mesa California USA:Global Energy and Water Cycle Experiment & World Climate Research Programme & United States National Oceanic and Atmospheric Administration & Office of Global Programs,2005.
[17] 曾红伟,李丽娟.澜沧江及周边流域TRMM 3B43数据精度检验[J].地理学报,2011,66(7):994-1004.
[18] 史岚.长江流域起伏地形下降水量分布精细化气候估算模型研究[D].江苏 南京:南京信息工程大学,2012.
[19] 张杰,李栋梁,何金梅,等.地形对青藏高原丰枯水年雨季降水量空间分布的影响[J].水科学进展,2007,18(3):319-326.
