低信噪比条件下快变多普勒频偏捕获算法*

赵 睿，王彦文

（中国矿业大学（北京）机电与信息工程学院，北京 100091）

低信噪比条件下快变多普勒频偏捕获算法*

赵 睿＊＊，王彦文

（中国矿业大学（北京）机电与信息工程学院，北京 100091）

针对卫星移动通信低信噪比条件下快变多普勒频偏捕获提出了一种新的算法即基于搜索空间压缩的谱线循环平移算法。首先，介绍了现有的载波频偏捕获技术，分析其不能适应快变多普勒频偏条件的原因;其次，分析了多普勒变化率对载波频偏捕获的影响，主要考虑一次变化率与二次变化率将严重限制低信噪比情况下对载波频偏估计时非相干累加的有效性;最后，在此基础上，提出了低信噪比条件下快变多普勒频偏捕获的基于搜索空间压缩的谱线循环平移算法。对算法进行的Matlab仿真结果表明，其具有2～3 dB的改善增益，与最大似然算法相比，在性能仅有0.2 dB损失的情况下运算量大大减少。

低地球轨道星座;卫星移动通信;高动态信号;载波捕获;快变多普勒频偏;低信噪比

1 引言

在卫星移动通信中，由于发送机与接收机的快速相对运动，使得接收信号会遭受“多普勒效应”的影响，接收信号将存在一个变化的多普勒频偏，此种信号称为“高动态信号”。尤其对于低地球轨道（LEO）星座卫星通信而言，接收信号的动态效应更加显著。卫星通信系统接收端载波同步分为载波捕获与载波跟踪，本文仅研究载波捕获。

针对载波频偏捕获问题，现有的载波频偏估计算法主要分为在时域中进行和在频域中进行两种。文献［1］提出了时域“基于自相关函数的改进Fitz算法”，利用自相关函数序列的差分代替自相关函数的相位估计载波频偏。在频域中进行的载波频偏估计主要是基于FFT运算，文献［2］提出了“基于分段FFT叠加的前向大频偏估计算法”，当不存在载波多普勒变化率或其很小时，此算法能较精确地给出多普勒频偏估计值，然而当多普勒变化率较大时，由于进行分段FFT运算产生的信号功率谱会发生“频域平移”现象，这将大大减小非相干累加的有效性，降低低信噪比条件下的检测性能。文献［3］对中频扩频信号进行平方，而后FFT处理，进行载波频偏估计。文献［4］提出对高动态扩频信号进行捕获时，首先利用卫星星历表估算出大致的多普勒频偏，然后采用串行搜索的办法逐次进行扫频，直到检测到相关峰的出现，从而进行多普勒频偏估计。文献［5］提出利用FFT实现载波频偏的快速捕获，但其只能适用于载波频偏小于符号速率的情况，并且所考虑的载波频偏为常数。文献［6］研究了利用自适应谱线增强器提高低信噪比条件下频偏检测的概率，也是针对载波频偏为常数的情况。因此，上述文献的方法仅适用于固定多普勒频偏或频偏变化率较小的情况。文献［7］研究了高动态多普勒频偏的估计，采用了最大似然算法对多普勒频偏、频偏变化率及频偏的二阶导进行估计，然而，此算法是基于三维搜索的思想，算法的计算量过于庞大。文献［8］与文献［9］研究了匹配傅里叶变换，然而，它只能估计出多普勒频偏的常数项与一次变化率，并且计算量与最大似然算法相当。本文在文献［7］和频域扫频技术的启示下，针对多普勒变化率对载波捕获的影响，提出了基于谱线循环平移的快变多普勒频偏捕获算法。

2 多普勒变化率对载波捕获的影响

若采用BPSK调制方式，接收信号表示为

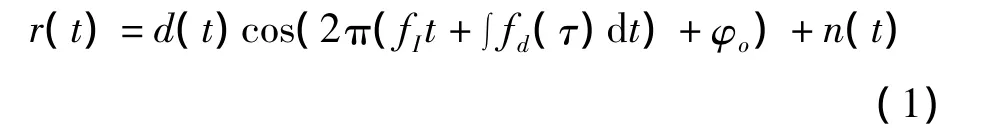
式中，d（t）为经成型滤波后的调制数据，fI表示中频调制频率，fd（t）表示快变多普勒频偏，φo表示初始相位，n（t）表示加性高斯白噪声。接收信号r（t）的解调器结构如图2所示。

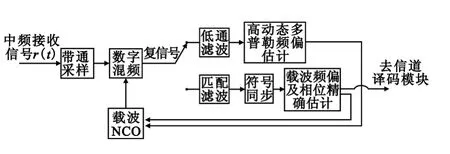
图1 具有快变多普勒频偏信号的解调器结构Fig.1 The demodulator structure with fast changing Doppler shift signal

图1中的高动态多普勒频偏估计模块，低通滤波器输出的复信号表示为

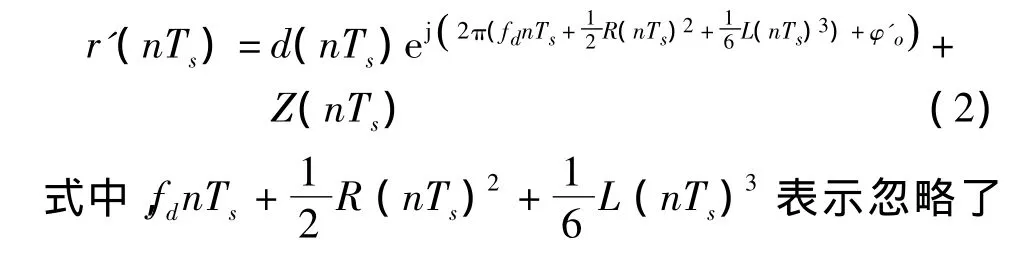
三次以上变化率的∫fd（τ）d t的泰勒级数展开，其中fd表示多普勒频偏的常数项，R表示一次变化率;L表示二次变化率;φ'o表示本地载波与接收信号的初始相差;Ts表示采样频率，一般是符号速率的整数倍;Z（nTs）表示复加性高斯白噪声。如果采样率远高于符号速率，可对r'（nTs）进行抽取，然后进行非线性处理，对于BPSK信号即平方运算，消除调制信息的影响，从而得到近似于正弦波的信号，再采用FFT进行频偏估计。然而，当R与L较大时，近似的正弦波信号会变为一次调频信号与二次调频信号，会对FFT频偏估计造成严重影响，下面进行详细分析。

2.1 多普勒频偏一次变化率对载波捕获的影响

对BPSK信号平方处理后，在遭受快变多普勒频偏影响下，信号趋近于调频信号，因此研究多普勒频偏一次变化率对载波捕获的影响，相当于研究一次调频信号的载波频率估计。一次调频信号表达为

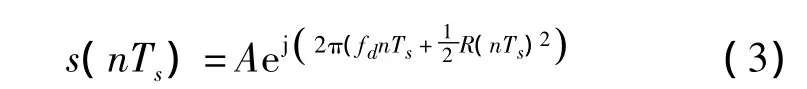
式中，fd表示常数项，R表示一次调频率，相当于多普勒频偏的一次变化率，A表示信号幅度。经分析，对于一次调频信号而言，峰值谱线对应的频率为本段采样信号的平均频率，表达为

式中，f0表示本段采样信号的起始频率，N为本段采样的点数。随着R的增加，不但发生了频谱平移现象，而且频谱幅度大大下降，峰值谱线消失，频谱出现“平台效应”，经研究发现，R越大，“平台效应”越显著，频谱幅度越低。

2.2 多普勒频偏二次变化率对载波捕获的影响

研究多普勒频偏二次变化率对载波捕获的影响，相当于研究二次调频信号的载波频率估计。二次调频信号表达为

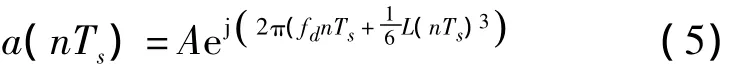
式中，fd表示常数项，L表示二次调频率，相当于多普勒频偏的二次变化率，A表示信号幅度。随着时间的增大，二次调频信号的频率会增大，导致了峰值谱线的平移，与一次调频信号不同的是频谱的平移量不再是一个定数，而是随时间的增大不断增大的一个量。和多普勒频偏一次变化率对载波捕获的影响相比，不但发生了频谱平移现象，而且频谱幅度大大下降，峰值谱线消失，频谱出现“平台效应”，与一次调频信号不同的是频谱的平台宽度不再是一个定数，而是随时间的增大不断增加的一个数。

经分析，若每段采样N个点，相继M段的二次调频信号的采样值，前后两段信号的峰值谱线所对应的频率差为

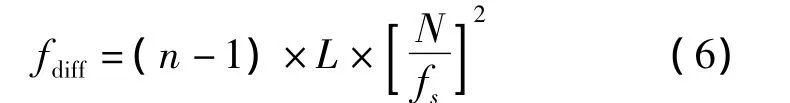
式中，n=1，2，3，…，M。二次变化率 L会导致峰值谱线幅度的下降及峰值谱线发生时变频域平移，甚至导致信号频谱产生“时变平台效应”，在二次调频信号的频率估计中，应坚决避免“时变平台效应”的发生，可通过合理选择N实现。

3 基于搜索空间压缩的谱线循环平移的快变多普勒频偏捕获算法

为了成功进行低信噪比条件下快变多普勒频偏捕获，本文提出基于搜索空间压缩的谱线循环平移算法，算法分两部分进行，一是压缩搜索空间，二是谱线循环平移。

3.1 压缩多普勒频偏搜索空间

考虑到多普勒频偏及其变化率的不确定空间很大，特别是对于工作频率为EHF频段的LEO星座卫星通信而言，情况非常严重，所以必须借助辅助手段压缩搜索空间，本文提出以下的压缩方法。

（1）由接收机载体的卫星导航终端或惯导设备提供载体的三维空间坐标SU=（xu，yu，zu）;

（2）由载体速度表、加速度表、加加速度表提供载体的速度信息VU=（vxu，vyu，vzu）、加速度信息AU=（axu，ayu，azu）及加加速度信息BU=（bxu，byu，bzu）;

（3）依据SU=（xu，yu，zu），由接收机存储的卫星星历表得知当前区域的覆盖卫星信息，从而得到当前覆盖卫星的瞬时三维坐标SS=（xs，ys，zs）、速度VS=（vxs，vys，vzs）、加速度AS=（axs，ays，azs）及加加速度BS=（bxs，bys，bzs）;

（4）计算得到载体速度在电波传播方向的分量

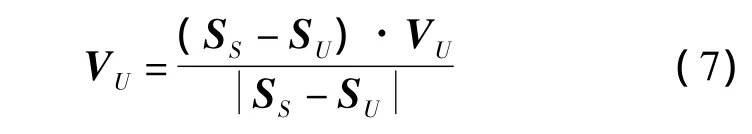
同理，得到卫星速度在电波传播方向的分量VS，也可得到载体、卫星加速度、加加速度在电波传播方向的分量 AU、AS、BU及 BS，式（7）中“·”表示矢量点积;

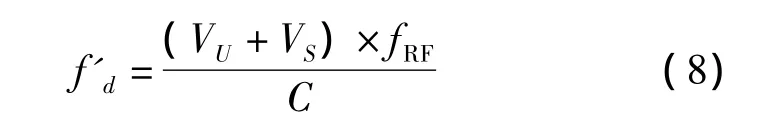
（5）计算得出多普勒频偏常数项大概估计值式中，fRF表示接收信号的射频标称频率。同理也可得出一次变化率的大概估计值R'及二次变化率的大概估计值L';

（6）将搜索空间压缩到估计的多普勒信息附近，空间大小由计算误差、星历表误差、接收机晶振稳定度等因素决定。

3.2 谱线循环平移算法

为了克服低信噪比条件下多普勒率的影响，本文提出以下谱线循环平移算法:

（1）对零中频信号进行每符号多点采样，并进行非线性处理。本文仿真中采用了BPSK信号，并进行了平方处理;

（2）将采样信号分成M段，每段N个采样点，分别进行NFFT点的FFT处理，并求模平方，将结果保存;

（3）依据要搜索的一次变化率及二次变化率的大小，对每段FFT结果进行一定循环平移，从而消除多普勒率对信号谱线的影响，这一步是本算法的核心思想。多普勒率较大时，信号频谱的频域平移破坏了非相干累加的有效性，算法的目的在于消除多普勒率的影响，增加非相干累加的有效性，从这一点考虑，算法将消除谱线的频域平移现象。设所搜索的一次多普勒率为Re，二次多普勒率为Le，信号采样率为fs，每段采N个样点，FFT点数设为NFFT，则第n（n=1，2，3，4，…，M）段 FFT 结果应当循环平移 Xn位，Xn分为两部分，一部分由Re引起，表示为XRn:

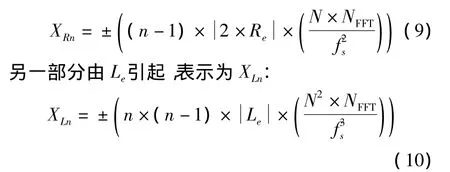
式（9）与式（10）中的正负号由Re与Le决定，当其为正，取正号，为负，取负号。Xn表示为

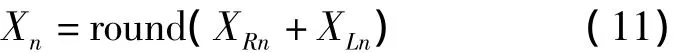
式中，round表示四舍五入的取整运算，当Xn为正值时，向左循环平移，为负值时，向右循环平移。经过以上处理，消除了谱线平移现象，使得M段FFT的谱线相重合;

（4）将循环平移后的FFT结果进行非相干累加;

（5）重复步骤1～4，搜索完所有多普勒率点;

（6）检测最大谱线峰值，进行频偏与多普勒率的估计。

此算法中的关键参数是FFT点数NFFT的选取，可以通过增大NFFT，提高对一次多普勒率R与二次多普勒率L估计的精度，NFFT每提高一倍，估计精度就提高一倍，但所要搜索的多普勒率的点数也增大一倍，从而使得平均捕获时间变大。

4 算法的性能仿真与计算量分析

以下对谱线循环平移算法进行性能仿真与计算量分析，并与最大似然算法（ML）进行比较，给出定量分析结果。

4.1 谱线循环平移算法的性能仿真

当机载终端以3倍音速运行，加速度为4倍的重力加速度（4g），采用的射频信号频率为1.2 GHz。图2是载波频偏 fd为4 012.5 Hz，多普勒率 R为175.5 Hz/s、L 为0 Hz/s2，FFT 点数 NFFT为1 024、采样率为19 200点/s及非相干累加段数M为8时，应用谱线平移算法前后的频偏检测概率。图3中载波频偏 fd为4 017.2 Hz，多普勒率 R、L、FFT 点数及非相干累加段数M与图2相同。

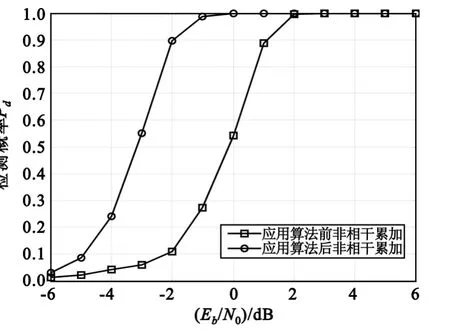
图2 fd为整数倍FFT分辨率时采用谱线平移算法前后的检测概率Fig.2 Detection probability before and after using translation algorithm when fd is integeral multiple of FFT spectral resolution

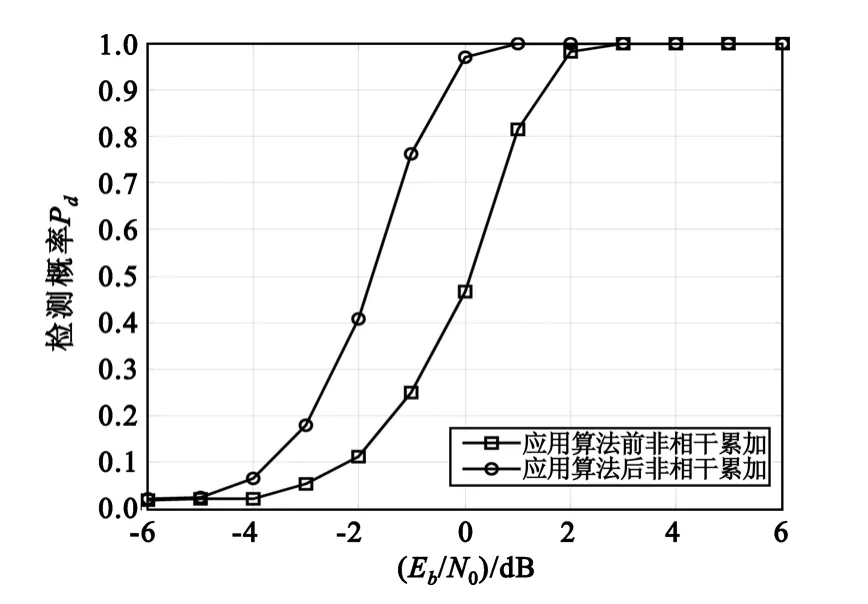
图3 fd位于整数倍FFT分辨率中间时采用谱线平移算法前后的检测概率Fig.3 Detection probability lines before and after using translation algorithm when fd locates in the middle of integeral multiple of FFT resolution

图2中，频偏恰好是FFT分辨率的整数倍，采用谱线平移算法，由式（9）、（10）计算得到，只要将FFT结果循环左移1位，便可消除多普勒率对非相干累加的影响。由图2可见，采用谱线平移算法后，相同检测概率时，信噪比改善了约3 dB。图3中，频偏恰好位于整数倍FFT分辨率中间，也是将FFT结果循环左移1位，消除多普勒率的影响，由图3可见，采用谱线平移算法后，信噪比改善约2 dB。采用谱线平移算法后，相同检测概率条件下，图3中要求的信噪比比图2要高1 dB，原因是由于图3中fd造成的频谱峰值比图2中的低。可见，谱线平移算法能消除多普勒率对非相干累加的影响，并能大大提高低信噪比条件下快变多普勒频偏检测的概率。

4.2 最大似然算法与谱线平移算法的比较

最大似然算法（ML）是参数估计的最优算法，以下就检测概率与计算量对ML与谱线平移算法进行比较。仿真条件:BPSK调制，信息速率为2 400 b/s，采样 速 率 为19 200点/秒，fd为4 012.5 Hz，R 为175.5 Hz/s，L 为0 Hz/s2，FFT 点数 NFFT为1 024，非相干累加数M为8。

图4是相同条件下ML与谱线平移算法的检测概率随信噪比的变化情况。当机载终端采用1.2 GHz射频信号，并以3倍音速运行，加速度为4倍的重力加速度（4g）。

由图4可见，相同检测概率时，ML所要求的信噪比比谱线平移算法低约0.2 dB，因此谱线平移算法略逊一点。

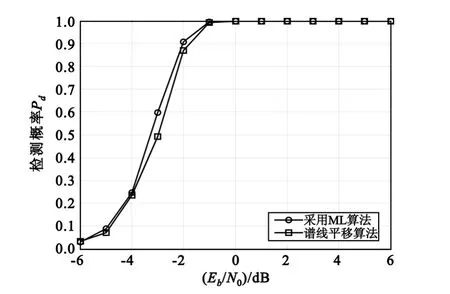
图4 ML与谱线平移算法检测概率的比较Fig.4 Comparison of detection probability between the spectral shift algorithm and ML

表1是ML与谱线平移算法计算量的比较，其中，NFFT为FFT点数，N为每段采样点数，M为非相干累加的段数，NR为所要搜索的一次多普勒率的个数，NL为要搜索的二次多普勒率的个数。由表1可见，谱线平移算法的复乘平方、FFT及模平方运算减低为ML的，并且比ML少了NR×NL×N×M次复乘运算。可见，谱线平移算法的计算量远小于ML，有利于实现低信噪比条件下快变多普勒频偏的快速捕获。

表1 ML与谱线循环平移算法计算量比较Table 1 Calculation amount comparison between ML and spectral shift algorithm

因此，综合考虑ML与谱线循环平移算法的性能与计算量，谱线循环平移算法占有明显优势。

5 结束语

本文研究了一种低信噪比条件下的快变多普勒频偏捕获算法。文中介绍了多普勒频偏一次变化率与二次变化率对载波捕获的影响，针对此影响，提出了适应快变多普勒频偏捕获的压缩搜索空间的谱线循环平移的大载波频偏捕获算法，给出了算法流程，通过MATLAB仿真，一方面证明了算法在低信噪比的快变多普勒频偏捕获中对非相干累加具有2～3 dB的改善增益，另一方面证明了与最大似然算法相比，谱线循环平移算法具有绝对优势。下一步工作将主要针对两方面研究:一是研究低信噪比条件下快变多普勒频偏的跟踪问题，即快变多普勒频偏的精确估计;二是考虑谱线循环平移算法的DSP或FPGA实现，具体考虑所要求的存储器资源、乘法器和加法器数量。低信噪比条件下快变多普勒频偏的捕获与跟踪技术在未来航空航天领域都有广阔的应用前景，因此，研究意义重大。

［1］孟庆萍，周新力，田伟.一种改进的Fitz载波频偏估计方法及其仿真［J］.电讯技术，2012，52（10）:1582 －1585.

MENG Qing － ping，ZHOU Xin － li，TIAN Wei.An improved Fitz carrier frequency offset estimation algorithm and simulation［J］. Telecommunication Engineering，2012，52（10）:1582 －1585.（in Chinese）

［2］ 叶展.卫星通信低信噪比接收技术与实现［D］.南京:解放军理工大学，2010.

YE Zhan.Satellite communications technology and achieve low SNR receiver［D］.Nanjing:The PLA University of Science and Technology，2010.（in Chinese）

［3］胡建波，杨莘元，卢满宏.一种基于FFT的高动态扩频信号的快速捕获方法［J］.遥测遥控，2004，25（6）:19 －24.

HU Jian－bo，YANG Zi－yuan，LU Man－ hong.FFT －based method for rapid acquisition of high dynamic spread spectrumsignal［J］.Journal of Telemetry，Tracking and Command，2004，25（6）:19 －24.（in Chinese）

［4］张伯川，张其善.高动态接收机的关键问题研究［J］.电子学报，2003，31（12）:1844 －1846.

ZHANG Bo－chuan，ZHANG Qi－shan.Research on the key issues of high dynamic receiver［J］.Chinese Journal of Electronics，2003，31（12）:1844 －1846.（in Chinese）

［5］陈大夫，高尔杨，珠江.快速傅立叶变换载波频偏估计算法［J］.电路与系统学报，2006，11（2）:128 －136.

CHEN Da－fu，GAO Er－ yang，ZHU Jiang.Fast Fourier Transform carrier frequency offset estimation algorithm［J］.Journal of Circuits and Systems，2006，11（2）:128 －136.（in Chinese）

［6］曹巍，罗霞，李晓亮.高动态低载噪比的载波捕获技术研究［J］.遥测遥控，2011，32（1）:43 －46.

CAO Wei，LUO Xia，LI Xiao － liang.High dynamic low carrier－to－noise ratio of the carrier capture technology research［J］.Journal of Telemetry，Tracking and Command，2011，32（1）:43 －46.（in Chinese）

［7］王晓湘，柯有安.高动态多普勒频率的最大似然估计器［J］.北京邮电大学学报，2000，23（1）:61 －65.

WANG Xiao－xiang，KE You－an.Maximum likelihood estimator of High Dynamic Doppler frequency［J］.Journal of Beijing University of Posts and Telecommunications，2000，23（1）:61 －65.（in Chinese）

［8］师栋锋，叶伟，贾鑫.匹配傅立叶变换及其应用［J］.装备指挥技术学院学报，2005，16（3）:87－90.

SHI Dong － feng，YE Wei，JIA Xin.Matching Fourier Transform and Its Applications［J］.Journal of the Academy of Equipment Command ＆ Technology，2005，16（3）:87 －90.（in Chinese）

［9］王盛利，李士国，倪晋麟，等.一种新的变换—匹配傅立叶变换［J］.电子学报，2001，29（3）:403 －405.

WANG Sheng － li，LI Shi－ guo，NI Jin － lin，et al.A New Transform － Match Fourier Transform［J］.Chinese Journal of Electronics，2001，29（3）:403 － 405.（in Chinese）

A Fast Changing Dopp ler Frequency Offset Acquisition Algorithm under Low SNR

ZHAO Rui，WANG Yan － wen
（Department of Mechanical Electrical＆ Information Engineering，China University of Mining ＆ Technology（Beijing），Beijing 100091，China）

A new algorithm or the spectrum line circle shift algorithm based on compressed searching space is proposed for fast changing Doppler frequency offset acquisition under low signal－to－noise ratio（SNR）for satellite mobile communication.Firstly，current carrier frequency offset acquisition technologies are introduced，and the reason why these technologies can not adapt to fast changing Doppler frequency offset acquisition is analyzed.Then，the effect of changing rate of Doppler frequency offset on carrier frequency offset acquisition is analyzed.The situation that the first order changing rate and second order changing rate affect carrier acquisition is considered emphatically.The changing rate of Doppler frequency offset seriously reduces the effectiveness of non－coherent accumulation during carrier frequency offset estimation at low SNR.Finally，on this base，the spectrum line circle shift algorithm based on the compressed searching space is provided and simulated with Matlab.The result shows that the algorithm has gain improvement of 2～3 dB.Compared with maximum likelihood（ML），the proposed algorithm losses 0.2 dB performance，however，amount of calculation is greatly reduced.

low earth orbit constellation;satellite mobile communication;high dynamic signal;carrier frequency offset acquisition;fast changing Doppler frequency offset;low SNR

TN911.72;TN914.42

A

1001－893X（2014）05－0553－06

10.3969/j.issn.1001 －893x.2014.05.005

赵睿，王彦文.低信噪比条件下快变多普勒频偏捕获算法［J］.电讯技术，2014，54（5）:553－558.［ZHAO Rui，WANG Yan－wen.A Fast Changing Doppler Frequency Offset Acquisition Algorithm under Low SNR［J］.Telecommunication Engineering，2014，54（5）:553 －558.］

2013－12－09;

2014－03－05

date:2013－12－09;Revised date:2014－03－05

＊＊

nzzrljn@163.com Corresponding author:nzzrljn@163.com

赵 睿（1974—），女，河南南阳人，2002年获硕士学位，现为讲师、博士研究生，主要研究方向为数字信号同步技术;

ZHAO Rui was born in Nanyang，Henan Province，in 1974.She received the M.S.degree in 2002.She is now a lecturer and currentlyworking towards the Ph.D.degree.Her research concerns digital signal synchronization.

Email:nzzrljn@163.com

王彦文（1962—），男，河北滦南人，1994年获博士学位，现为教授、博士生导师，主要研究方向为工业安全网络化监控、智能电网同步技术等。

WANG Yan － wen was born in Luannan，Hebei Province，in 1962.He received the Ph.D.degree in 1994.He is now a professor and also the Ph.D.supervisor.His research concerns industrial safety network monitoring and smart grid synchronization.