亚指数索赔额下带随机收益的非齐泊松风险模型的破产概率

张耀东

(重庆理工大学数理统计学院，重庆 400054)

亚指数索赔额下带随机收益的非齐泊松风险模型的破产概率

张耀东

(重庆理工大学数理统计学院，重庆 400054)

研究了非齐次泊松风险模型和带随机收益的更新风险模型中的有限时间的破产概率。当初始资本趋近于无穷大，在索赔额服从亚指数分布时的假设下，得到了一个有限时间的渐近公式。主要在江涛2009年论文的基础上，把正交变换子族的结论推广到亚指数族的情形，并得到了一些结果。

随机收益;非齐泊松;亚指数;有限时间破产

1 模型的建立

1.1 基本模型

有一个由摄动引起的简单的更新风险模型，在这个模型中索赔额{Xn，n=1，2，…}是由一组独立同分布(i.i.d)的随机序列且是非负的随机变量，由共同的分布(d.f.)F=1-F与索赔到达的时间δn，n=1，2，…组成的一个更新计数过程 N(t)=max{n≥1：δn≤t}，t＞0。

它有常数的强度λ，习惯上记max{φ}=0。带渉动项δ0W0(t)的保险公司在时间t时的总盈余为U(t)，它满足方程

其中：u＞0为保险公司的初始盈余;c为常数收取的保费。{B0(t)，t≥0}为标准布朗运动，如果索赔时间的间隔 δ1，δ2- δ1，…，δn- δn-1，n=2，3，…有共同的分布，那么该模型称作 C-L 模型。

在C-L模型中，若参数λ是时间的函数，那么{N(t)，t≥0}称作非齐的泊松过程，其中风险强度函数为{λ(t)，t≥0}。如果对任意的 t有 s＞0，则 N(t)满足

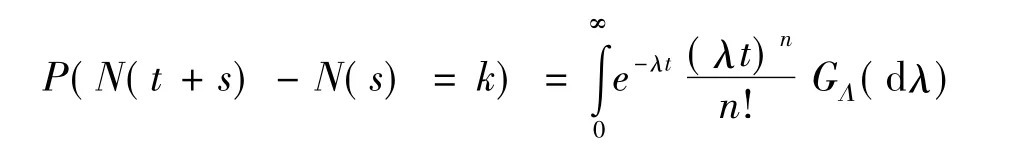
其中，GΛ是Λ的分布函数，那么{N(t)，t≥0}称作条件泊松过程。

在本文中如无特殊说明，所有的极限关系均为u→∞，A～B和A≿B分别表示为=1和≥1。

1.2 随机收益

许多人都在研究更新风险模型和重尾索赔下的更新风险模型，还有一些学者在风险模型中考虑了风险投资。如果保险人将资本投资到风险市场，就会产生风险资产，为了简单起见，假设资本价值可以看作一个特殊的几何布朗运动，即

其中：{B(t)，t≥0}是一个标准布朗运动;μ，δ分别称作期望收益率和波动扩散系数且满足μ≥0，δ≥0。众所周知，上式有下面的解：

因此，在时间t内，投资达到风险市场的盈余可表示为

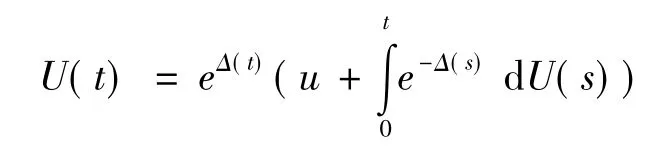
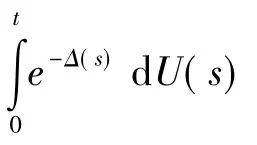
这个模型与上文提到的由渉动引起的简单的更新风险模型的主要区别在于：这里将带有渉动的随机利率考虑进去了。因此，将第1个盈余表达式代入到第2个盈余表达式中得到一个新的模型。

2 相关结果

重尾子族在保险和金融风险中起着重要的作用，可以用来描述大的索赔额。下面给出几个非常重要的重尾子族。

长尾子族L：分布函数F属于L，当且仅当

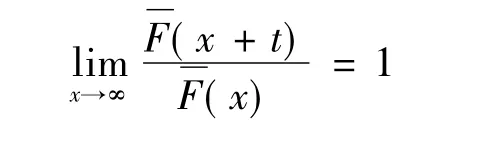
对任何t成立，等价于对t=1成立。

一个分布族属于正交变换族R-α，当且仅当x)=x-αL(x)，当 x→∞时，L(x)为长尾变化函数。

亚指数族S：分布函数F属于S，当且仅当

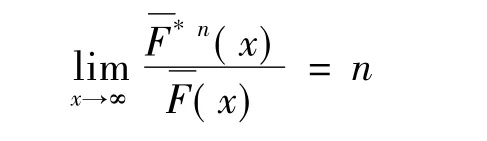
对任何的n成立，等价于对n=2成立，其中Fn*(x)代表F的n重卷积，这些长尾子族满足如下的包含关系：

最终破产概率的渐近行为在风险理论中起着重要的作用。1982年Embrechts和Veraverbeke建立了一个非常著名的渐近关系，当索赔额的分布为亚指数分布时，最终破产的概率满足

江涛在文献［5］和［6］中获得了一些推广的结果。本文应用江涛在2009年论文中提到的方法，得到了一些新的结论。

3 几个引理

下面的引理1来自Ross写的随机过程。

引理 1{N(T)}t≥0为 Poisson 过程，{δk，k≥1}为到达的时间，在 N(T)=n 的条件下，对任何 T ＞0，随机向量(δ1，δ2，…，δn) 的分布与随机向量(TU(1，n)…TU(n，n)) 的分布相同，其中(U(1，n，)，…，U(n，n)) 为(0，1)上独立同分布的顺序统计量，它们与随机向量U1，…，Un具有一致的分布［5］。

引理2对于更新风险模型，如果F∈L∩D，那么有限时间T破产概率满足［1］

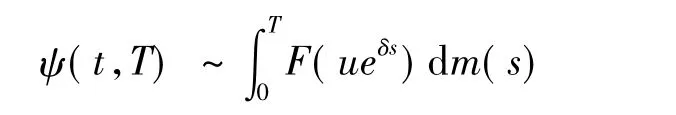
引理3令{Xi，1≤i≤n)}是独立同分布的亚指数族，有共同的分布F。那么0＜a≤b＜∞，对所有的 a≤ci≤b，1≤i≤n，有［1，7］

引理4对于更新风险模型，如果F∈L∩D，那么有限时间T破产概率满足［1］

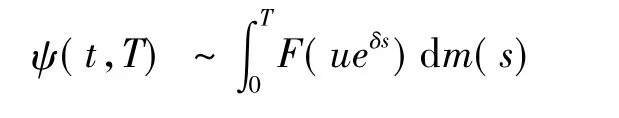
引理5如果B(t)是标准布朗运动，那么B(t)的任意阶矩存在［7］。

4 主要定理

定理1考虑参数为{λ(t)，t≥0}的非齐泊松模型，且假设资本价值满足下面的随机摄动

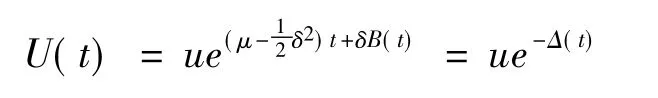
那么，到时刻t的盈余为

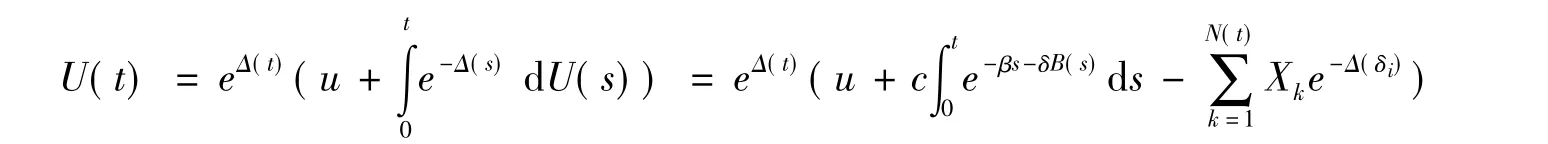
如果索赔额的分布F∈S，那么

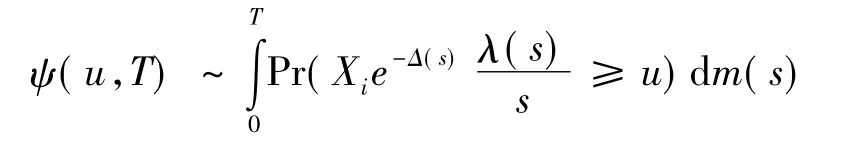
证明盈余表达式可变形为

成立，其中

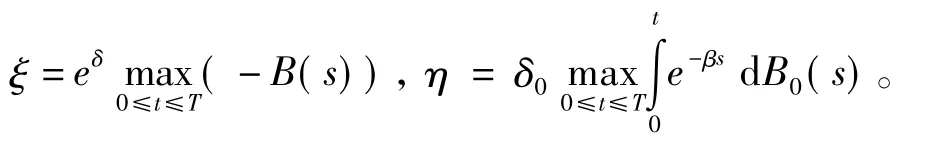
由Ross［6］可知，N(t)是强度为λ(t)的非齐泊松过程，可以看作强度为λ的齐次泊松过程，其中λ(s)≤λ。N(t)对应的事件Ai发生，相当于在时间δi以概率λ(δi)/λ发生。

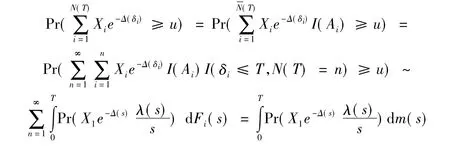
上面的等价式用到了引理3中亚指数索赔额的概率与求和可交换性，及更新函数m(t)=Fi(s)。

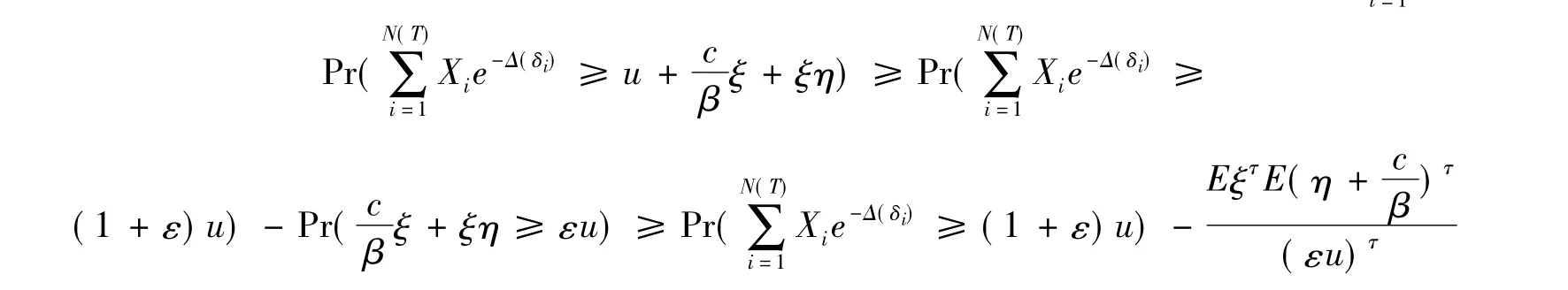
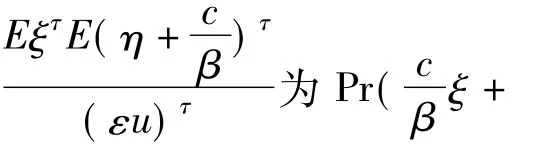
另一方面，

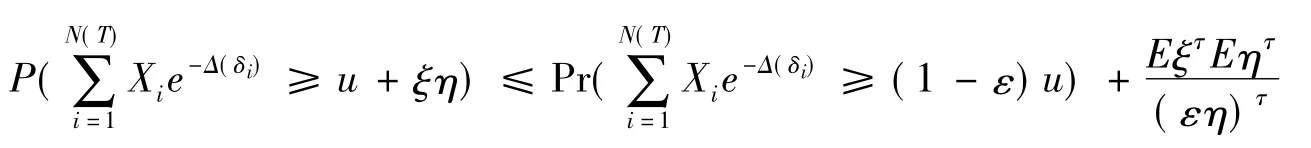
类似地，

评论1 这个结果与江涛在文献［1］中假设F∈R-α得到的结论

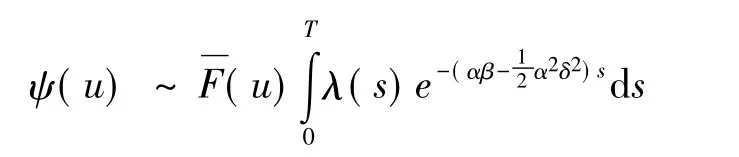
有些类似，而在亚指数族时并不会有F(x)=x-αL(x)这样的性质。

定理2考虑条件泊松过程，即对任意的t，s＞0，N(t)满足

其中Λ以GΛ为分布函数(d.f.)，其他条件同定理1，如果F∈S，那么

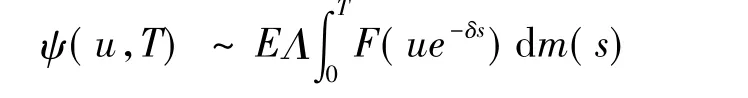
证明应用条件概率公式

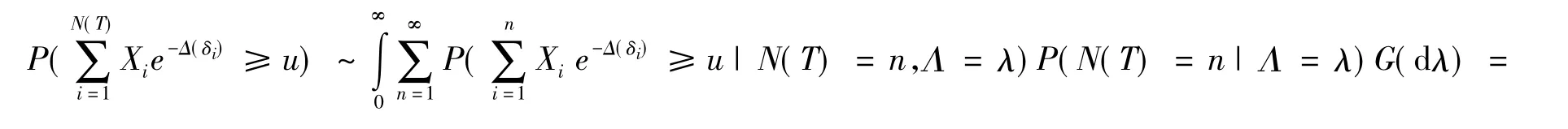
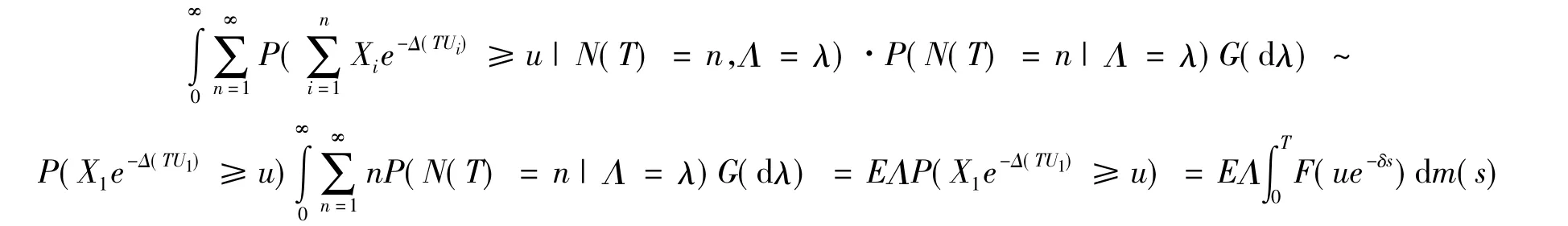
评论2 这个结果是江涛在文献［1］中假设F∈R-α得到

结果的推广。

［1］ Jiang T.Ruin probability for nonstandard Possion risk model with stochastic return［C］//Proceedings of the World Congress on Engineering.U.K.：London，2009.

［2］ Asmussen S.Subexponential asymtotics for stochastic processes：extreme behavior，stationary distributions and first passage probabilities［J］.Ann Appl Probab，1998，8(2)：354-374.

［3］ Asmussen S，Kalashnikov V，Konstantindes D，et al.A local limit theorem for random walk maxima with heavy tails［J］.Statist Probab Letters，2002，56(4)：399-404.

［4］ Tang Q.The finite time ruin probability of the compound passion model passion model with constant interterst force［J］.Appl Probab，2005，42(3)：608-619.

［5］ Ross S M.Stochastic processes［M］.New York：John Wiley ＆ Sons，Inc.，1983.

［6］ Karatzas I，Shreve S.Brownian Motion and Stochastic Calculus［M］.Berlin：Springer，1988.

［7］ Tang Q.The ruin probability of a discrete time risk model under constant interest rate with heavy tails［J］.Scand Actuarial J，2004：229-240.

Ruin Probability for Subexponential Claimed Sizes Non-homogeneous Possion Risk Model with Stochastic Returns

ZHANG Yao-dong
(1.School of Mathematic，Chongqing University of Technology，Chongqing 400054，China)

We studied the ruin probability with stochastic returns for non-homogeneous Poisson risk model and subexponential claimed size in renewal risk model.An asymptotic formula for the ruin probability was divided when initial surplus approaches infinity and the claimed sizes obey subexponential distribution.Based on the conclusions of paper of Jiang Tao 2009［1］for the orthogonal transformation subfamily，we extend to the case of the subexponent，and get some results.

stochastic returns;non-homogeneous Poisson;subexponential;finite-time ruin

O211.9

A

1674-8425(2014)10-0137-06

10.3969/j.issn.1674-8425(z).2014.10.026

2013-12-26

重庆市教委科技项目(KJI120805)

张耀东，男，硕士研究生，主要从事数理统计研究。

张耀东.亚指数索赔额下带随机收益的非齐泊松风险模型的破产概率［J］.重庆理工大学学报：自然科学版，2014(10)：137-142.

format：ZHANG Yao-dong.Ruin Probability for Subexponential Claimed Sizes Non-homogeneous Possion Risk Model with Stochastic Returns［J］.Journal of Chongqing University of Technology：Natural Science，2014(10)：137-142.

(责任编辑 刘 舸)