探析教学中向量相关理论的引入

徐文华

（重庆工商大学 派斯学院 基础部，重庆 401520）

探析教学中向量相关理论的引入

徐文华

（重庆工商大学 派斯学院 基础部，重庆 401520）

为了让向量的有关理论更加具体，使学生能够直观地理解，本文通过系统地探讨线性方程的相关问题，并将这些问题和向量的一系列定义有机的结合起来，从而揭示了向量的一系列定义在线性方程中的意义，使向量的有关理论更加具体、直观。通过这种方式的引入，学生在学习向量的有关定义定理的时候，能够对这些抽象的定义和定理有一个更加感性地认识，尤其是在学习n（n＞3）维向量的时候。

向量；线性方程；关系；引入

一、引言

目前，高校线性代数教材，在介绍n维向量空间的有关理论中，经常是先介绍怎样解线性方程组和判断一个线性方程组有没有解，接着介绍向量的线性表示、向量组的线性表示、向量组等价、向量的线性相关性，向量组的极大无关组等概念，然后利用线性方程组这个工具来分析和判断一个向量能否用另外一些向量线性表示，一组向量是否线性相关等这些概念。虽然很多学生通过学习，知道向量中的这些问题怎么解决，但是，对于向量的这些定义，仍然感觉很抽象，没有实际意义，尤其对于维数超过三维的向量，很难找到出直观的几何解释。究其原因，关键在于学生不知道为什么要定义这些东西，有什么样的作用，其实，向量空间中的很多定义就是为解决线性方程组的相关问题而生。下面，本文通过论述线性方程组的相关问题，从中提出问题，进而引入解决方法——即向量的方法，进而揭示向量的有关定义和方程组的有关理论之间的联系。

对于向量的有关定义和方程组的有关理论之间的联系，也有人做过类似的探讨.[3]中，作者将向量和有向线段联系起来，进而揭示向量空间中相关定义的意义，但作者的这种引入局限于二维和三维的向量，对于维数超过三维的向量，无法通过有向线段来分析。[4]中，作者是根据线性方程组的向量形式谈及向量的关系，如今的线性代数教材中多数以谈及到这个问题，而本文要论述的方程和向量的关系是另外一种关系。[5]中，作者仅探讨了向量组的关系和其次线性方程组解的关系，但没有系统地探讨向量的其他关系和线性方程组的联系。

二、线性方程组的线性相关性

在实际应用中，为求解某些问题，我们设定n个变量x1，x2，…xn，并为这些变量建立了m个等式关系，假定这些等式是如下形式的线性方程：

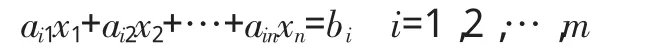
为求解这些变量，我们将这些等式构建成如下的线性方程组，记为方程组A，

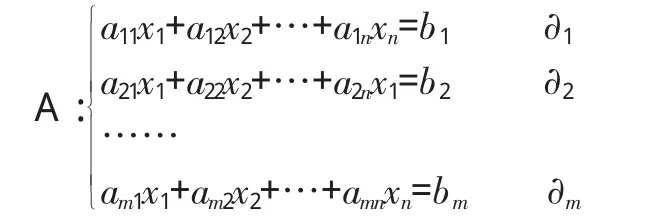
其中的方程依次记为∂1，∂2，…∂m。那么对于方程组A，有如下问题需要考虑：

1.方程组中方程和方程之间有没有关系？有什么样的关系？

2.方程组有没有同解方程组，同解方程组和原方程组之间的方程又有什么关系？

3.方程组的解和方程组中方程的解有什么样的关系？

为了便于探讨这些问题，不妨根据线性方程组的一些规律给出一些定义和命题，以便说明问题。在一个线性方程组中，经常会有一个方程可以通过另外的方程恒等变换得到，比如方程组中一个方程等于另一个方程等式两边同乘一个常数，或一个方程等于另外某些方程相加等等。

定义1：若方程组A中存在某个方程∂i可以通过另外方程恒等变换得到，则称方程组A为线性相关的方程组，否则称为线性无关的方程组。

显然，若方程组A中的方程∂i可以通过方程组A中其他的方程∂k1，∂k2，…∂kn恒等变换得到，我们可以认为方程∂i代表的等式关系相对于方程∂k1，∂k2，…∂kn来说是重复或是多余的，不防称方程∂i为方程∂k1，∂k2，…∂kn的重复方程。因此，线性相关的方程组一定有重复方程，而线性无关的方程组则无重复方程。

命题1：若方程β1可以通过方程组A中的方程∂1，∂2，…∂m恒等变换得到，则方程组A的解（若有解），一定是方程β1的解。

证明：方程组的恒等变换一般有两种：

1.方程∂等式两边同乘一个公因子k，等式保持不变，记为k∂。

2.方程∂1和方程∂2等式两边对应相加等式保持不变，记为∂1+∂2。

若方程β1可以通过方程组A中的方程∂1，∂2，…∂m恒等变换得到，则存在一k1，k2，…km使得β1=k1∂1+k2∂2+…+km∂m。

若x1=t1，x2=t2，…xn=tn，是方程组A的任意一组解，则将x1=t1，x2=t2，…xn=tn代入方程∂1，∂2，…∂m中，方程等式仍保持不变，对这些方程作如下变换：k1∂1+k2∂2+…+km∂m，可知，得到的等式仍保持不变，所以x1=t1，x2=t2，…xn=tn也是方程k1∂1+k2∂2+…+km∂m的解，即x1=t1，x2=t2，…xn=tn是β1的解。

由命题1不难得出下述推论：

推论1：若方程组B中的方程β1，β2，…，βn可以通过方程组A中的方程∂1，∂2，…∂m恒等变换得到，则方程组A的解（若有解），一定是方程组B的解。

推论2：若方程组B中的方程β1，β2，…，βn和方程组A中的方程∂1，∂2，…∂m可以相互恒等变换得到，则方程组A和方程组B为同解方程组。

三、向量和线性方程的关系

介绍了方程组的线性相关性，那么，如何判断一个方程组是线性相关的方程组，以及一个方程和另外的方程的关系呢？联系高斯消元法，我们知道，解线性方程组是通过构造方程组的增广矩阵，利用矩阵的初等行变换来完成高斯消元法的过程。因此，我们可以定义方程的矩阵来研究方程和方程之间的关系。

（1）k∂，相当于∂的方程等式两边同乘一个公因子k得到的方程。

（2）∂1+∂2，相当于∂1的方程与∂2的方程等式两边对应相加得到的方程。

因此，方程和方程之间的关系与方程的向量与向量之间的关系是可以对应起来，有时甚至是等价的。下面，我们来看看，向量空间中的一些定义在方程理论中所代表的意义。

若存在一组数k1，k2，…，ks使得β=k1∂1+k2∂2+…+kn∂n，则称向量β可由向量组∂1，∂2，…，∂n线性表示[2]。这是线性表示的定义，由上面的讨论知，这个定义在方程中的意义是向量β的方程可由向量∂1，∂2，…，∂n的方程通过恒等变换得到，并且向量∂1，∂2，…，∂n的方程组的解是向量β的方程的解。因此，在引入向量线性表示定义的时候，我们可以说，为了研究方程组中方程和方程之间的关系或一个方程能否通过其他方程恒等变换得到，于是有了线性表示这样一个概念。

若有两组向量A：{∂1，∂2，…，∂s}和B：{β1，β2，…，βt}，若向量组A中的向量都可由向量组B中的向量线性表示，则称向量组A可由向量组B线性表示。若向量组A和向量组B可以相互线性表示，则称向量组A和向量组B等价[2]。该定义表明，若向量组A可由向量组B线性表示，则向量β1，β2，…，βt的方程组的解是向量∂1，∂2，…，∂s的方程组的解。若向量组A和向量组B等价，则向量β1，β2，…，βtt的方程组和向量∂1，∂2，…，∂s的方程组是同解方程。因此，在引入向量组线性表示和向量组等价的时候，我们可以说，为了研究一个方程组和另一个方程组解的关系，于是有了向量组线性表示和向量组等价的定义。

对于n维向量组∂1，∂2，…，∂s，若存在不全为零的数k1，k2，…ks使k1∂1+k2∂2+…+ks∂s=O，则称向量组∂1，∂2，…，∂s线性相关，若仅当k1=k2=…=ks=0时，上式才成立，则称向量组∂1，∂2，…，∂s线性无关[2]。由向量组线性相关的另一等价条件：向量组∂1，∂2，…∂s（s≥2）线性相关的充要条件是其中至少有一个向量能被其余向量线性表示[2]，知该定义在方程组代表的意义是：若向量组∂1，∂2，…∂s线性相关，则向量∂1，∂2，…∂s的方程组是线性相关的方程组，方程组中有重复方程，也就是说向量∂1，∂2，…∂s的方程组中至少存在一个方程可由其余方程恒等变换得到。若向量组∂1，∂2，…∂s线性无关，则向量∂1，∂2，…∂s的方程组是线性无关的方程组，即方程组中无重复方程。

向量组∂1，∂2，…∂s的一个部分组∂i1，∂i2，…，∂ir线性无关，并且∂1，∂2，…，∂s中的每个一个向量都可由∂i1，∂i2，…，∂ir线性表示，则∂i1，∂i2，…，∂ir称为它的极大无关组[2]。在向量空间中，我们知道向量组的极大无关组和向量组是等价的，因此，在线性方程组中，这个极大无关组的意义是：向量∂i1，∂i2，…，∂ir的方程组是向量∂1，∂2，…，∂s的方程组的同解方程。也就是说，对于一个线性相关的方程组，我们可以从中选出部分方程构成方程组，这个方程组可以和原方程组是同解的，而选择的这部分方程是原方程组向量的极大无关组所对应的方程。因此，在引入极大无关组的定义的时候，我们可以说为了在线性相关的方程组中选出部分和原方程组同解的方程组，于是有了极大无关组这样一个概念。另外向量组中极大无关组所含向量的个数称为向量组的秩[2]，实际上，在线性方程组中，向量组∂1，∂2，…，∂s的秩，就是向量∂1，∂2，…，∂s的方程组中线性无关的方程的个数。

四、实例分析

有如下线性方程组A和B：

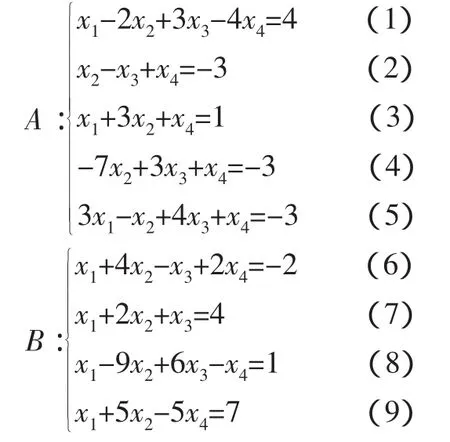
方程组A中，方程的向量分别为∂1=（1，-2，3，-4，4）T，∂2=（0，1，-1，1，-3）T，∂3=（1，3，0，1，1）T，∂4=（0，-7，3，1，-3）T，∂5=（3，-1，4，1，-3）T。方程组B中，方程的向量分别为β1=（1，4，-1，2，-2）T，β2=（1，2，1，0，4）T，β3=（1，-9，6，-1，1）T，β4=（1，5，0，-5，7）T。下面我们通过向量的关系回答上文中对方程提出的一系列问题。下面我们将这些问题具体化。

1．方程组A中，方程和方程之间有没有关系？

根据向量中判断向量组线性相关、线性无关的理论，由

2．在方程组A中，方程（5）和其他的方程有什么样的关系？或者说方程（5）能否由其他的方程恒等变换得到？若能，是怎么恒等变换得到的？

要回答这个问题，其实就是回答向量∂5能否由向量∂1，∂2，∂3，∂4线性表示？若能，表达式是怎样的？

根据向量中判断一个向量能否由其他向量线性表示的理论，由

知∂5能由向量∂1，∂2，∂3，∂4线性表示，且线性表示是唯一的，∂5=∂1+2∂2+2∂3+∂4。因此知，方程（5）能由方程（1）、（2）、（3）、（4）恒等变换得到。方程（5）是相对于方程（1）、（2）、（3）、（4）的重复方程，其方程的关系可简示为：

（5）=（1）+2×（2）+2×（3）+（4）

3．方程组A和方程组B是否为同解方程？

4．方程组A是线性相关的方程组，那么从中选出哪些方程构成方程组可以同解与原方程组？

要回答这个问题，其实就是回答向量组∂1，∂2，∂3，∂4，∂5极大无关组是什么？根据极大无关组的理论，由

知∂1，∂2，∂3，∂4，∂5的极大无关组有∂1，∂2，∂3，∂4或∂1，∂2，∂3，∂5。因此，方程（1）、（2）、（3）、（4）或者是（1）、（2）、（3）、（5）构成的方程组和原方程组是同解的，且原方程组中线性无关的方程最多只有4个。

四、结语

通过对线性方程和向量的关系的讨论，我们发现方程的线性关系和向量的线性关系完全可以对应起来，因此向量和向量组的定义和性质，同方程组联系起来就有了实际意义，不再是抽象的概念。学生通过这种联系，可以更直观的理解向量空间中的一些定义。通过实例分析可以看出，分析线性方程的某些关系也即是分析其方程向量的关系，因此，通过线性方程的关系引入向量的关系的这种方式，能够使向量的关系更具实际意义，而不再是抽象的定义。

[1]北京大学数学系几何与代数教研室代数小组.高等代数（第二版）[M].北京：高等教育出版社，1988：104-126.

[2]袁晖坪，郭伟.线性代数（第一版）[M].北京：高等教育出版社，2010：94-104.

[3]吴克仁.对“向量线性相关性”教学法的探讨[J].上海工程技术大学教育研究，2004，（2）：28-30.

[4]孙志信.谈向量的线性关系、矩阵的秩与求解线性方程组的关系[J].佳木斯教育学院学报，1993，（2）：60-63.

[5]赵玉环.向量组关系与其构造的其次线性方程组的解的关系探讨[J].工科数学，1999，15（4）：146-149.

G642.3

A

1674-9324（2014）26-0150-04

徐文华（1984-），女，汉；湖北随州人；工作单位：重庆工商大学派斯学院；硕士；主要研究方向：应用数值代数。