基于B样条插值的高精度型面测量路径规划
2014-01-24李建普
李建普
(河南省机械设计研究院有限公司,河南 郑州 450002)
基于B样条插值的高精度型面测量路径规划
李建普
(河南省机械设计研究院有限公司,河南 郑州 450002)
为了解决型面检测时测量路径的规划问题,提高型面测量的效率和精度,本文针对单光束激光三角法非接触式型面检测专用测量系统,提出了基于B样条曲线插值的测量路径规划模型。针对影响单光束激光测量精度和效率的因素:景深范围、测头倾角等,利用B样条曲线插值模型规划出测量点的位置,使测量运动路径紧密结合型面曲率变化,提高了实际测量精度及效率,解决了大型型面测量的路径规划难题。
型面检测;路径规划;B样条插值;激光三角法
随着激光三角法测量技术非常广泛的应用,大型自由曲面测量路径规划问题成为测量时的重点难题之一。自由型面的设计主要是利用B样条拟合数据点生成型线,然后扩展至整个型面。本文在结合前人研究的基础上针对激光三角法自由曲面测量的特点提出了B样条曲线插值的型面测量路径规划模型。
1 路径规划的研究
1.1 路径规划的主要内容
针对自由型面模型的测量路径规划目标是根据型面点及测头信息,对待测点进行规划,得到能够反映曲率变化的测点;其测量方式一般首先沿设计型线进行点测,再沿型线垂直方向逐步扩展至整个型面。本文根据型面测量实际,主要针对型线测量的路径规划进行研究。
1.2 测量约束条件研究
在本研究中采用激光三角法进行实际测量,其测量景深有限,同时要始终保持激光的入射方向与被测点的法线重合(如图1)。约定被测点的法线与入射激光方向不重合时称被测表面发生了倾斜,其夹角称为倾角θ。倾角是影响测量精度比较大的一个方面,因此研究路径规划对提高测量系统精度、效率具有重大意义。
在测量中要求测头始终保持在最佳测量位置以提高测量精度,所以要根据被测表面的形状,使测头和工件表面保 持固定距离,使得测头的运动轨迹与被测表面变化相同。
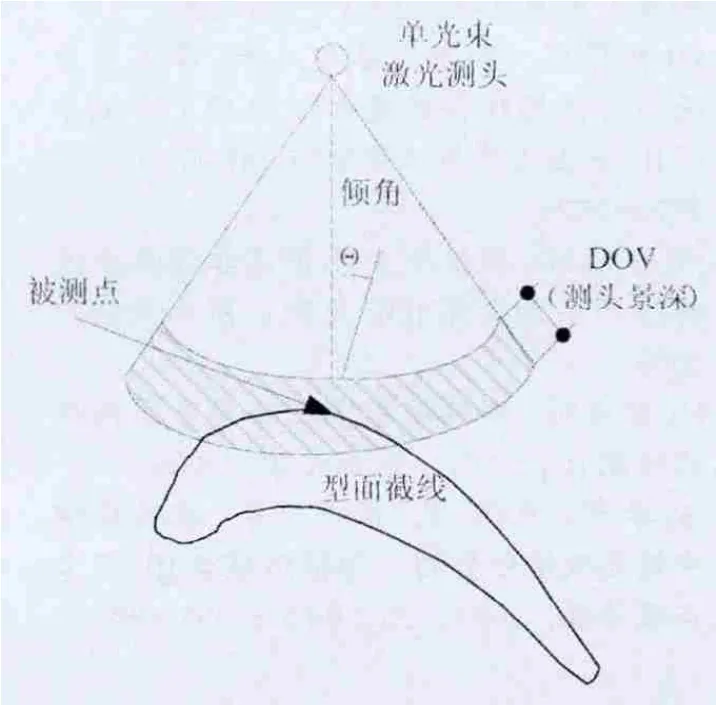
图1 测量约束条件示意图(俯视)
实际检测中如何根据理论数据点及测量约束条件,求出实际测头位置是关键点。本文提出首先采用B样条插值法求得已知型面理论曲线;然后根据测量约束条件(入射光线与测点垂直),求取型面理论点的法矢;最后根据景深限制,在被测点法矢方向上取最佳位置作为测量路径规划位置(如图2)。
由型面造型过程可知,型面截面线一般设计为光滑连续曲线。为保持设计、检测的一致性,所以要采用三次非均匀B样条插值求取型面的表达曲线,以使曲线全部通过型值点。
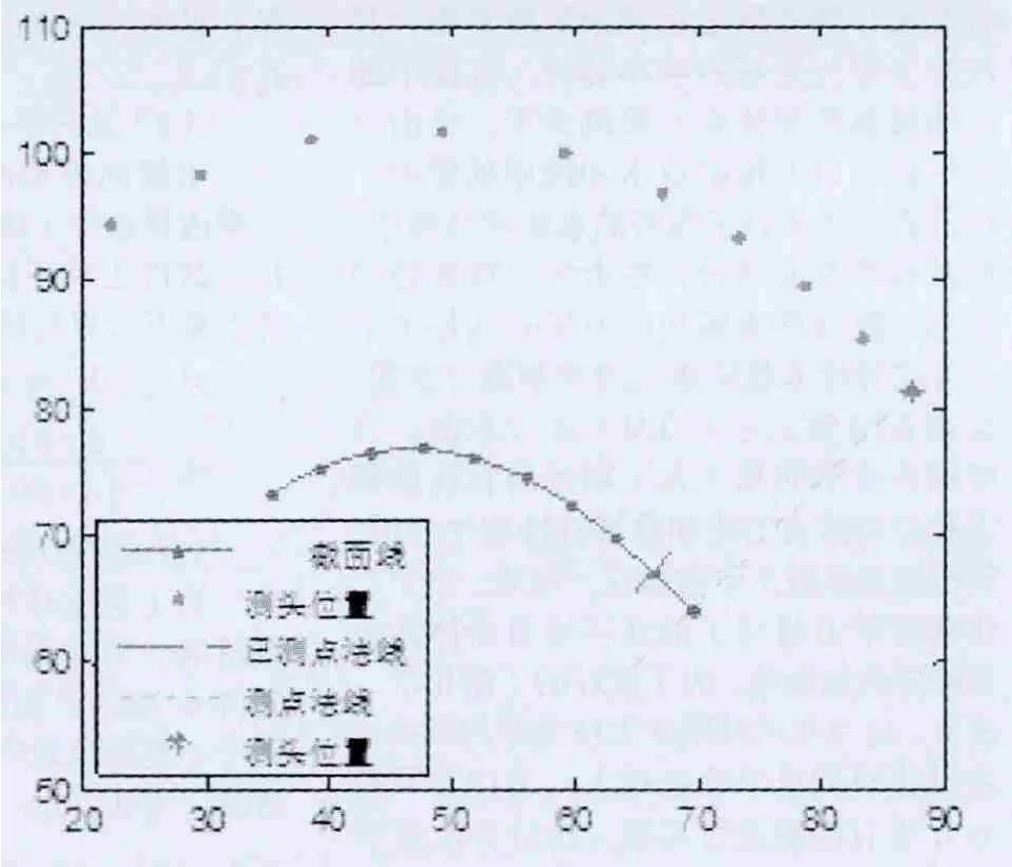
图2 B样条插值型面测量路径规划
1.3 B样条曲线的定义及B样条插值



。由于型面设计中,型线上各相邻点之间的空间距离很可能相差很大,本文选用三次非均匀B样条来实现测量路径的规划。B样条插值又被称为反算B样条控制点,由已知曲线型值点,根据B样条函数理论求出其控制顶点。在进行B样条控制点反算时,首先应根据给定的型值点构造节点矢量U,再根据节点矢量上的节点集算出相应的基函数;而后求得反算控制点的方程组;最后对此方程组求解,求得非均匀B样条曲线的控制顶点。
2 型线的B样条插值反算
2.1 数据点参数化
欲唯一地确定一条插值于n+1个数据点 的参数插值曲线,必须先给数据点 赋予相应的参数值,使其形成一个严格递增的序列,称为数据点的参数化。其中每个参数值称为节点,它决定了位于插值曲线上的数据点与其参数域内的对应点之间对应关系,即点有节点值 。由于型面线为光滑、连续曲线,本文采用积累弦长参数化法,型值点 对应参数 由递推公式求取:
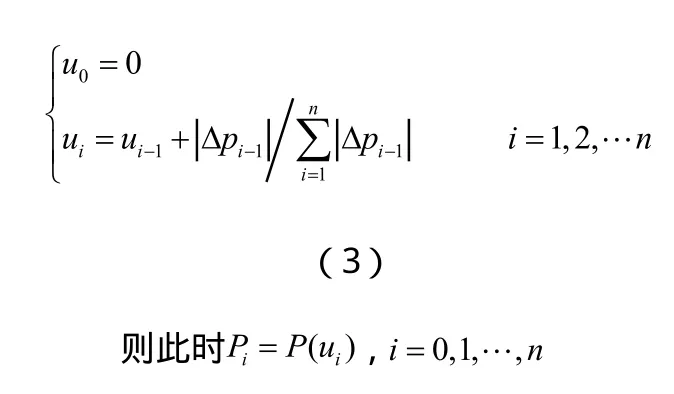
2.2 节点矢量的确定


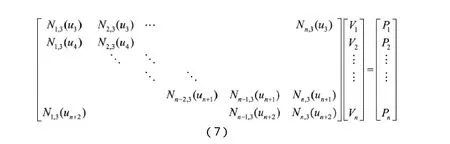

2.3 三次B样条基函数确定

2.4 反算 控制顶点计算

把插值曲线定义域内的节点值带入由式(1)(5)得到n+1个数据点
的三次B样条插值曲线方程,应该满足插值条件即:

其中系数矩阵元素均为三次B样条基函数的值,只与节点值有关,由递推式(2)求得,利用拟追赶法求解该方程,就得到了控制顶点。有了这些特征多边形顶点,就可以依据这些点通过B样条插值出实际曲线,曲线轮廓上任意点均可通过插值求得。利用B样条曲线特性计算出各型值点的切矢,为求测量路径点做好准备。
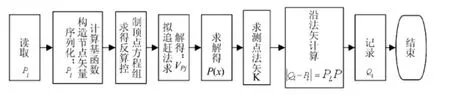
图3 算法实现流程图
2.5 型线被测点的法矢确定
型面测量过程受激光三角法测量倾角的约束,本文采用直射式激光三角法则需要求得被测点的法矢。B样条曲线上一点处的r阶导矢 递推公式为:

即k次B样条曲线的r阶导矢相当于k-r次B样条曲线,但求导矢顶点递推公式与参数u无关,而所求导矢与参数u有关。由于本文采用三次非均匀B样条插值法求取型面线,则可以采用公式(8)计算其上被测点的切矢,然后求取切矢的倒数即可求得被测点的法矢。其切矢的计算公式为:

3 路径规划算法实现
通过上述步骤求取被测截面线的法矢,则根据型面测量的景深约束条件求取最佳测量位置,即沿被测点法矢方向取被测点的最佳测量位置作为测量点,求取所有被测点的测量位置即为此型面线的测量路径。算法具体实现流程:1)读取被测理论型面线坐标点集,并序列化;2)根据N+1个理论型面点 构造节点矢量,算出相应的基函 数;3)根据式(9)求得三次B样条插值曲线的反算控制点方程组;4)拟追赶法求解反算控制顶点方程组,得控制顶点;5)根据式(2)求解得样条插值曲线P(x);6)利用式(10)计算被测点的法矢k;7)沿法矢方向求取测量位置;8)重复1)-7)直至型面被测点计算完毕,并保存所求测量路径如图3。

图4 测头路径规划结果
4 试验验证
为了验证三次非均匀B样条插值路径规划效果,本文采用某一封闭截面轮廓数据为实例进行验证。规划测点坐标,并针对理论截面数据生成B样条曲线及测量路径如图4,测量路径符合型面曲率变化,且路径变化在景深范围内,满足了高精度型面测量的要求。
结语
本文针对激光三角法精密型面测量,提出了基于B样条插值路径规划模型,并行了详细的论述和说明。通过构造三次B样条插值曲线规划测量点,使测头运动路径紧密结合型面变化,解决了测头景深范围的影响;利用采得型面点法线方向控制测头倾角的影响,提高了测量精度。从试验看出本文模型是实现高效率、高精度型面测量的有效方法。
[1]来新民,黄田,陈关龙.自由曲面数字化的自适应规划[J].上海交通大学学报,1999,33(07):838-841.
[2]徐骅,张秋菊.针对叶片型面检测的激光测量系统的规划及相关研究[J].汽轮机技术,2006,48(01):76-80.
[3] 杨仁平,张国雄,刘水桂,等.回转曲面测量技术[J].天津大学学报,2005,38(05):385-390,(03):272-277.
[4] 胡俊,王宇晗,李晔,蔡建国.基于曲线外插技术的曲面测量等弧长采样方法[J].机械科学与技术,2004(23).
[5]K-C Fan. A non-contact automatic measurement for free-form surface profile,Computer Integrated Manufacturing Syetems, 1997, 10(4):277-285.
[6]Seokbae Son, Seungman Kim, Kwan H.Lee. Path planning of multi-patched freeform surfaces for laser scanning,International Journal of Advanced Manufactural Technology,2003,22:424–435.
[7]何雪明,李成刚,胡于进,等.三坐标测量机测量路径的曲率连续自适应规划[J].清华大学学报(自然科学版),2007,47(S2):1835-1839.
[8]梁锡坤. B样条类曲线曲面理论及其应用研究[D].合肥工业大学,2003.
[9]Lee KH, Son S-B, Park H-P. An automated scanning system for freeform surfaces, Proceedings of ICC & IE,2000,Beijing, 11–13.
[10]Funtowicz F, Zussman E, Meltser M.Optimal scanning of freeform surfaces using a laser-stripe, Israel-Korea Geometric Modeling Conference, 1998,TelAviv,Israel, 47–50().
[11]Seokbae Son, Hyunpung Park,Kwan H. Lee. Automated laser scanning system for reverse engineering and inspection, International Journal of Machine Tools & Manufacture,2002,42:889–897.
TP391
A
10.13612/j.cnki.cntp.2014.07.085
