家具设计专业实践课学生成绩模糊综合评价研究
2014-01-23鲁群霞
■鲁群霞 郭 琼
(华南农业大学林学院,广东广州 510642)
家具设计专业实践课学生成绩模糊综合评价研究
■鲁群霞 郭 琼
(华南农业大学林学院,广东广州 510642)
模糊数学自1965年由美国著名控制论专家L.A.Zadeh第一次提出“模糊集”的概念及有关方法以来,发展十分迅速,已被应用于各个领域[1]。长期以来,如何对学生成绩做出合理、公平、科学的综合评价是教育工作者一直探索的问题之一[2]。将模糊数学导入教育教学评价,可克服学生成绩评定中大量模糊现象,促进了教育质量评价的量化[3-7]。家具设计专业实践课程集艺术、科学和技术于一体,学习过程中要求学生同时具备材料、加工工艺、机械等工科背景,美术、文学、设计等艺术基础和大量的课外实践。由于专业实践课涉及面广,作业过程灵活,所以考核学生专业成绩,应该用一种综合性评价方法。本文以笔者长期讲授的《非木质家具设计》课程为案例,导入模糊数学对学生成绩进行综合评价,以期为家具设计专业实践课教学评价提供参考。
1 家具设计专业实践课评价存在的主要问题
华南农业大学于2004年开设木材科学与工程专业(家具设计与制造方向),培养具有木材科学与技术学科的基础理论、家具设计与制造的专业知识和技能,掌握家具设计与制造工艺理论与加工方法,具备较扎实的家具材料、结构、工艺、设备、管理知识和创新设计能力的应用型毕业生,授予工科学士学位。根据本校2012年修订的本科人才培养方案,该方向开设的设计专业实践课主要有:《素描》、《色彩》、《设计表现技法》、《造型设计基础》、《家具结构设计》、《家具设计》、《非木质家具设计与制造》、《家居产品设计》、《模型设计》等课程。根据以往的教学实践经历,家具设计专业实践课学生成绩评价具有以下特点:(1)教师评定成绩往往带有较大的主观性、片面性。由于每个教师专业背景不同,有些教师重视学生作品的概念新颖与否,有些教师重视实际的生产技术、材料选择或工艺制设计专业实践课程评价具有灵活性和全面性。与传统理工科课程相比,设计实践课程没有固定试卷,无法用考卷来评价学生学习情况。
2 模糊评价原理
2.1 确定评价因素集
针对评价对象选取评价因素,即确定评价的指标体系,评价指标体系由一群组合特定、彼此间相互联系的测评指标组成,实质上是教学评估标准的具体化。评价因素集用X表示:X = {x1,x2,……xn},其中,Xi(i = 1,2,3…n)表示一级因素,在一级因素中又可包含多个二级因素:
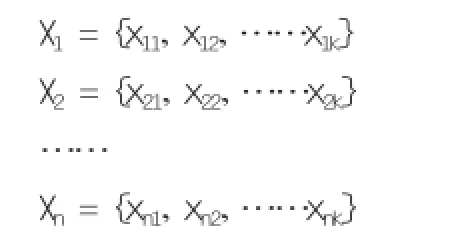
2.2 确定评语集
对评价对象进行评价,要选取合适的评语集,评语集用Y表示:Y = {y1,y2,……ym}。例如,用“优、良、中和差”表示学生课程成绩与标准成绩的相似程度,则评语集为:{优,良,中,差}。
2.3 确定评价因素权重
确定各因素对评价对象的影响程度,并将其量化形成权重集,用A表示:A = {a1,a2,……an}。二级因素的权重集分别为:
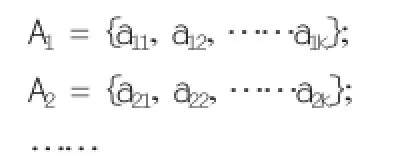

■图1 《非木质家具设计》学生成绩评价体系

表1 某学生成绩测评得分表

以上权重集中的各权重值可用主观加权法、专家加权法、德尔菲咨询法、层次分析法计算。
2.4 建立模糊矩阵和综合评价多级模型
如果为单因素评价,则有由X到Y的模糊映射,即:f:X→Y。映射f可确定一个模糊关系Xi→f(Xi)=(ri1,ri1,……rim)∈F(Y),Rf(Xi,Yi)= f(Xi)(Yi)=rij。因此Rf可由模糊矩阵R表示。

于是(X,Y,R)构成一个综合评判模型,在这个模型中,对于给定的A 是Y 的一个模糊子集。
若因素集是二级模型,则从低层次开始转换,设Xi为一层因素X的子集,先对Xi中诸因素做单因素评价,如Xi中诸因素的权重分配Ai(i= 1,2,3…n),Xi的综合评判变换矩阵为Ri(i= 1,2,3…n),则Xi的判断结果Bi= AiRi(i= 1,2,3…n)。总的判断矩阵为R,综合判断结果为B:
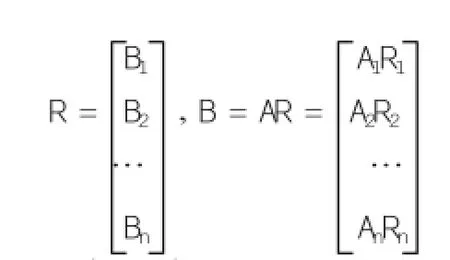
依据上述原理,可以构建三级、四级模型。
2.5 综合评价值计算
综合评价值可由W = B H T计算出,式中H为等级矩阵,H T 为H 的转置矩阵,可直接得到该名学生的标准分值。
3 模糊评价模型构建
以《非木质家具设计》课程为例,设定模糊评价体系,构建评价模型。其他设计专业实践课的模糊评价模型与此相类似,只对个别一级、二级指标或权重作相应调整。
3.1 确定评价因素集X
运用德尔菲(Delphi)法向10位具有丰富教学经验的家具设计专业课任课教师进行专家咨询,汇总提炼考核《非木质家具设计》学生成绩的主要指标,并对重要性程度进行评判,汇总得到各指标及权重。包括学习态度x1、设计创意x2、设计表现x3和方案陈述x4共4个一级指标,每个一级指标又分解成3-5个二级指标,共计14个二级指标。
3.2 确定评价因素的权重
运用专家评判法,对各个因素权重进行打分,结果为:

3.3 考核方法
考核采用以教师评价为主,学生互评为辅的办法。将3名学生分为一个学习小组,每名学生的成绩,教师评价占70%,另外2名学生的评价占30%。因此,权重分配矩阵P= {0.7,0.3}。评价时分别在4个评价等级{优,良,中,差}上做是或否二值逻辑判断,即某个评价要素属于某个级别时,则在相应的级别对应栏中填写“是”或“否”,则模糊关系矩阵R中的元素rij计算公式为:

4 实例分析
如表1以某个学生的评价结果,计算该学生的综合评价成绩。
4.1 教师对某学生的综合评价
(1)学习态度
模糊评价矩阵R1:
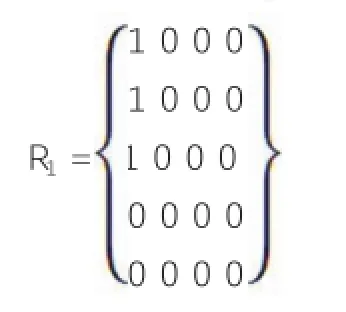
评价结果B1为:
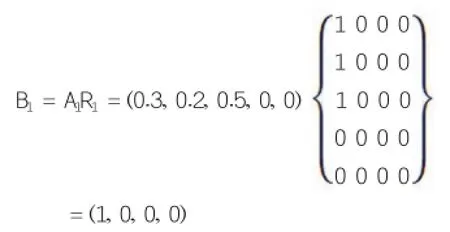
按“最大隶属度”原则,教师对某学生的“学习态度”评价结果为“优”。
(2)设计创意
模糊评价矩阵R2:

按“最大隶属度”原则,教师对某学生的“设计创意”评价结果为“良”。
(3)设计表现
模糊评价矩阵R3:
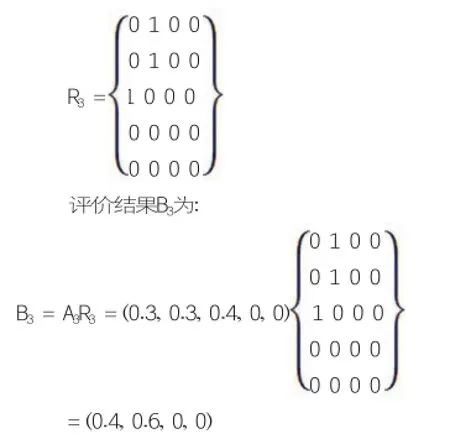
按“最大隶属度”原则,教师对某学生的“设计表现”评价结果为“良”。
(4)方案陈述
模糊评价矩阵R :

按“最大隶属度”原则,教师对某学生的“设计表现”评价结果为“良”。
因此,教师对某学生的综合评价模糊关系矩阵:

4.2 小组内同学对某学生的综合评价
同理,可以计算同组的2名同学对某同学的综合评价结果为:

根据最大隶属度原则,该学生的综合评价为“优”。由于实际操作中,需要将等级成绩换算成具体的分数。设定等级矩阵H={95,85,75,55},则可计算该名同学的标准分为:
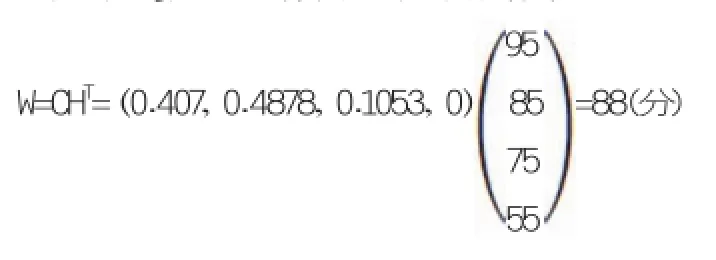
5 结论与讨论
模糊评价尺度按“优、良、中、差”设计,符合人脑逻辑思维规律,操作起来比较容易。教师只需按照设计的评价表打“1”或“0”,其余计算、统计工作可在Excel中完成,数据可靠性高,在很大程度上消除了人为“印象分”的影响,增强了所得数据的客观性。模糊综合评判法的定量分析要比传统的定性描述更加科学和精确,在主观指标得分与客观指标得分之间构建了有机联系的桥梁。评价中采用的等级得分和百分制得分的互通,使得该评判法将主客观指标结合在一起评价时,具有较好的整体性和适用性。
教学实践证明,用模糊综合评判法来评定学生平时成绩较为客观、公正和科学,它克服了传统考核办法中的主观与片面性,同时又能有效地提高了学生平时学习的积极性。然而,该评价方法要比平常使用的方法复杂,评价中计算过程比较多,而且每门具体课程评价指标体系会略有不同,因此,可利用编程语言开发简单易用的软件,并根据具体课程调整评价指标名称和权重等来计算。此外,模糊综合评价方法也可应用在家具设计研究领域中[8],如评价家具设计方案的优劣等。
(责任编辑:方 舟)
[1]彭祖赠,孙韫玉.模糊数学及其应用[M].武汉:武汉大学出版社,2007,78-114.
[2]吴海英,张杰.学生成绩排名的综合评价模型[J].大学数学,2006(4):142-145.
[3]方育坤.用模糊数学方法评价学生的设计成绩[J].理工高教研究,1997(4):53-55.
[4]荆宁宁,张惠恩.本科毕业论文模糊评价系统研究[J].系统工程理论与实践, 2001(11):94-99.
[5]吴长悦,申立群,李小光.基于模糊数学的测量实习成绩评定[J].测绘通报,2004(1):60-66.
[6]张卓.模糊综合评判法在学生平时成绩考核中的应用[J].广州大学学报 (社会科学版).2009,8(5):62-64.
[7]徐焰,汤韶敏,廖钰珊等.普通高校体育课程学生成绩多元化评价体系的构建[J].武汉体育学院学报,2010,44(11):89-93.
[8]陈祖建,蒋松林,关惠元.基于层次分析法的家具设计方案评价模型[J].林业科学,2010,46(12):130-136.
Study on the Students’ Performance Comprehensive Evaluation of Furniture Design Courses Based on Fuzzy Mathematics
Lu Qunxia & Guo Qiong
本文运用德尔菲法设定家具设计专业实践课学生成绩评价指标体系,确定一级指标和二级指标的权重,导入模糊数学和学生参与式评价,最终建立了一套合理、公平、科学的家具设计专业实践课学生成绩模糊综合评价系统。
家具设计;课程成绩;模糊数学;综合评价
The evaluation indices of students’ performance on furniture design courses and its weight were formed by Delphi, including Primary indices and secondary indices. Based on fuzzy mathematics and student’s participation in evaluation, a set of reasonable, fair and scientifc comprehensive evaluation system of students’ performance on furniture design courses was established.
Furniture design; Student performance; Fuzzy mathematics; Comprehensive Evaluation
TS664.0;TS611
A
1006-8260(2014)07-0070-03
华南农业大学教育改革项目(编号:JG09146)
